一种用于匹配场反演的遗传算法

张学磊，冯杰



一种用于匹配场反演的遗传算法

张学磊，冯杰

(中国电子科技集团公司第三研究所，北京100015)

遗传算法在接近全局最优解时，存在搜索速度变慢、过早收敛、个体的多样性减少很快、甚至陷入局部最优解等问题。通过在遗传算法中引入模拟退火因子、混沌因子和多样性测度因子，在很大程度上克服了原有遗传算法的早熟、局部搜索能力差的缺点。同时，又能发挥原有遗传算法的强大的全局搜索能力，保证了改进后的混合遗传算法能较好地收敛于其全局最优值。

匹配场反演；遗传算法；模拟退火；混沌；多样性测度

0 引言

匹配场法反演经常涉及到几个，甚至十几个待定参数的反演问题，可以看成是一个非线性的、有众多局部最优点的全局优化问题。传统的搜索方法，如穷举法，在现有的计算条件下，所耗费的时间是一个天文数字，是难以承受的；又如局部搜索算法，这种算法的最终解只是某个局部最优解，往往不是全局最优解，而且最终解的质量还严重依赖于初始解的选择。智能优化算法，又称为现代最优化算法，从一组随机生成的初始个体出发，按照一定的规则，并根据适应度(代价函数值)大小进行个体的优胜劣汰，提高新一代群体的质量，再经过多次反复迭代，逐步逼近全局最优解，而且这种算法一般具有严密的理论依据，理论上可以在一定的时间内找到全局最优解或近似全局最优解。常用的智能优化算法有神经网络优化算法、遗传算法(Genetic Algorithm, GA)[1]、模拟退火算法(Simulated Annealing, SA)[2]等。由于遗传算法在海洋地声参数反演方面已经得到了广泛的应用[3]，并得到了很好的结果，因此本文将采用遗传算法作为反演的全局优化算法。

1 遗传算法的缺点、改进方向

遗传算法是借鉴生物界自然选择和自然遗传机制的随机化搜索算法。它通过模拟自然选择和自然遗传过程中发生的繁殖、交叉和基因突变现象，将问题的求解表示成“染色体”的适者生存过程。在每次迭代中都保留一组候选“染色体”，并按某种指标从种群中选取较优的“染色体”，利用遗传因子，也就是选择因子、交叉因子和变异因子，对这些“染色体”进行组合，产生新一代的候选种群，重复此过程，直到满足某种收敛指标或达到设定的最大代数为止。

由于遗传算法主要的遗传操作都是在一定概率条件下随机发生的，因此，它在为种群中个体提供进化机会的同时，也不可避免地产生退化的可能，使得在接近全局最优解时搜索速度变慢、过早收敛、个体的多样性减少很快、甚至陷入局部最优解。其中很大原因要归咎于遗传算法对现实生物演化过程过于简化的模拟。而实际上，遗传算法中的群体是伪多样性的：首先，初始化群体的多样性难以实现；其次，即使假设传统的初始化方法可以保证初始群体在空间上均匀分布，但并不能保证它们在质量上也是均匀分布的；最后，群体的多样性在选择压力下也很难保持。因此，改善群体的多样性是提高遗传算法性能的重要研究方向，即设计产生的初始群体与遗传因子。

模拟退火算法一种随机组合优化方法，它模拟热力学中固体退火的过程，并广泛应用于组合优化问题，是局部搜索算法的扩展[4]。它同局部搜索算法一样，具有强大的局部搜索能力，不同于局部搜索之处是其改变了只接收优化迭代的准则，在一定范围内接收恶化解。将模拟退火算法与遗传算法结合，来解决遗传算法局部搜索能力的不足。

混沌[5,6](Chaos)是一种普通的非线性现象，貌似一片混乱实则具有内在的规律性。Logistic映射作为重要的混沌映射之一，定义为一种不可逆映射: (0, 1)→(0, 1)。对于某个变量，其第+1个值由式(1)所示的Logistic映射迭代得到：

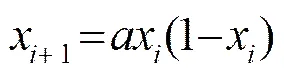
式中，是个重要参数，当=4，系统输出可在(0, 1)上取到不重复的任何值，三个不动点(0.25，0.5，0.75)除外。

2 混合遗传算法的构造

由第1节的分析可知，在遗传算法的基础上，将遗传算法、模拟退火和混沌有机结合，优势互补，发挥各自的优势，克服遗传算法(GA)局部搜索能力差、伪多样性、早熟现象等问题，就可构造出一种快速准确的搜索算法——混合遗传算法(Hybrid GA, HGA)。

2.1 群体的多样性的改进

利用混沌映射的优秀特性，同时针对本文的实际问题，首先将待反演参数空间进行归一化，即进行变换：

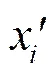
(3)

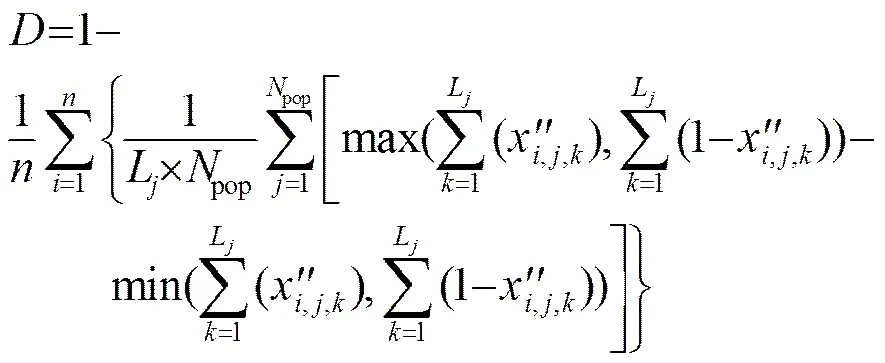
或：(5)

当种群的多样性测度减小时，种群有早熟趋势。图1给出了在一次反演过程中，种群的多样性测度的函数值随进化代数的变化图，可以认为遗传算法30代以后种群进入了早熟状态，由此引出早熟定义：当种群的多样性测度函数值在连续代内，变动幅度小于设定值时，可认为种群进入早熟状态。此时需要对进行种群的多样化处理。当种群的多样性测度函数值小于设定值，且未达到最大收敛代数时，需要重新对种群中的不良个体进行处理，以改善种群的多样性。用随机数发生器产生一个的随机数，对全体个体中个劣质个体，按照式(2)进行全参数空间的混沌操作，产生新种群中的个新个体。

2.2 局部搜索能力的改进[8]

模拟退火作为局部搜索算法的改进算法，与局部搜索算法不同之处在于采用Metropolis准则，并用一组称为冷却进度表的参数控制算法进程。Metropolis准则为：模拟退火处于状态和状态的几率的比值等于相应Boltzmann因子的比值，即：

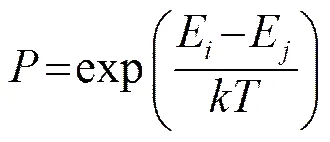
式中：为冷却进度表参数中的温度控制参数(在海底参数反演领域，Gerstoft[1]给出了一个较好的设定：设定为每一代中染色体适应度函数值的最小值)，若>1，则始终接是收状态；若<1，则用随机数发生器产生一个的随机数，若>，则接受状态为新状态，否则舍弃状态。在遗传算法产生新种群的新染色体时，将按照Metropolis准则决定是否接收新产生的染色体。

2.3 遗传算子的改进

在遗传算法的进化过程中，影响种群收敛性的最重要的参数为交叉因子和变异因子。为了防止因早熟得不到全局最优解，将、设计成种群多样性测度函数的函数，Gerstoft[1]曾给出了设定：=0.8、=0.05，以此为蓝本设定本文中交叉因子和变异因子：

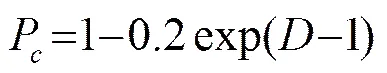
(8)

3 混合遗传算法的具体实现步骤

(2) 将所有个体译为二进制编码；

(3) 计算种群中每个个体的适应度函数。判断是否满足结束条件，若是则算法终止运行并输出最终结果，若否，进入步骤(4)；

(4) 判断是否满足结束条件，若是则算法终止运行并输出最终结果，若否，将每个个体按照适应度函数值进行排序，决定温度控制参数，进入步骤(5)；

(5) 按照式(3)和式(4)，计算种群的多样性测度函数值。按照早熟定义判断种群是否进入早熟状态，若进入早熟状态，转至步骤(7)，若否，转至步骤(6)；

(6) 按照式(7)和式(8)计算交叉因子P、变异因子P，对父代进行选择、交叉和变异操作，产生子代，计算子代中个体的适应度函数值。按照Metropolis准则，决定是否接受子代中的当前染色体。在上述过程中保留最佳染色体，而后转至步骤(4)；

(7) 用随机数发生器产生一个[0,1)的随机数，舍弃全体个体中个劣质个体，并按照式(1)进行全参数空间的混沌操作，产生新种群中的pop个新个体，并将之译为二进制编码，计算子代中个体的适应度函数值，转至步骤(4)。

4 混合遗传算法与改进前遗传算法的性能比较

4.1 仿真实验环境设定

以两层海底模型作为基准测试模型，见图2。海水中声速从海平面的1480 m/s单调下降到海底(海平面下40 m处)的1460 m/s，声源频率采用三个频率：100、200、300 Hz，声源深度为20 m，接收器阵为垂直阵，阵元共有16个，间距为2 m，分布于2~32 m的海水中。声源与接收器的间距为=5 km，沉积层厚度2=30 m、声速1=1600 m/s、密度sed=1.7 g/cm3、衰减系数sed=0.23 dB/λ，基底的声速2、密度b、衰减系数b分别为：1700 m/s、1.85 g/cm3、0.23 dB/λ。

假定上面的某些参数为未知，设定其搜索范围，即可对算法性能进行仿真。待反演参数设定为：声源与接收器间距为、海水厚度1、以及沉积层的声速1、密度sed和衰减系数sed。

4.2 混合遗传算法性能仿真结果

在仿真实验中，采用非相干的Bartlett匹配器，其定义如下：

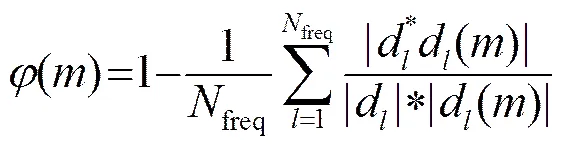
CASE1 加入所有因子的情况

CASE2 无多样性测度因子情况(包括混沌因子)

CASE3 无多样性测度因子、无交叉概率和变异概率自适应因子的情况

CASE4 无多样性测度因子、无模拟退火因子的情况

CASE5 无多样性测度因子、无模拟退火因子、无交叉概率和变异概率自适应因子的情况

在每种情况下，遗传算法独立运行100次，基因的总数为256^5≈1.0995×1012个。遗传算法在每次运行时，调用的基因总数为6400次。对遗传算法最终的输出结果进行统计分析，不同信噪比下的仿真结果(见表1、表2和表3)表明，改进后的HGA较原有的遗传算法有更加优异的寻优性能。这具体表现在：HGA待反演参数的均值更加接近于预设值，其标准差更小。

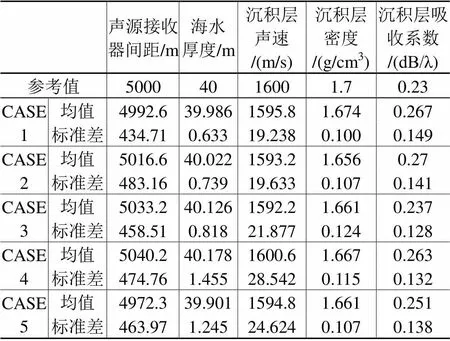
表1 无噪声时算法性能仿真结果

表2 SNR=3 dB的算法性能仿真结果

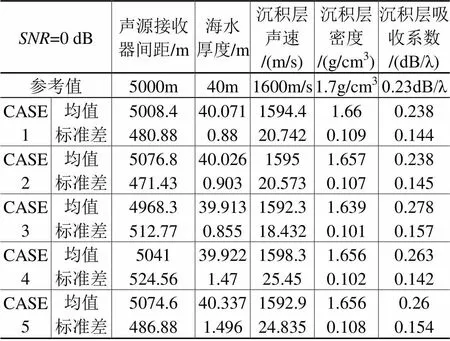
表3 SNR = 0dB的算法性能仿真结果

5 结论

本文提出一种用于匹配场反演的遗传算法，并进行了计算机仿真分析。仿真分析结果表明，改进后的HGA可以将遗传算法、模拟退火、混沌各自的优点结合起来，扬长避短，并引入了多样性测度因子来监测种群的多样性，随时改善种群性能以及动态自适应调节交叉概率和变异概率，使得进化前期交叉明显，后期变异显著，更符合遗传规律。改进措施在很大程度上克服了原有遗传算法的早熟、局部搜索能力差的缺点，同时，发挥了原有遗传算法的强大的全局搜索能力，保证了改进后的混合遗传算法能较好地收敛于其全局最优值。

致谢：本文对应的研究工作得到了中国科学院声学研究所李整林研究员的指导，在此表示感谢。

[1] Gerstoft P. Inversion of seismoacoustic data using genetic algorithms and a posteriori probability distribution[J]. J. Acoust. Soc. Am, 1994, 95(2): 770-781

[2] Lindsay C E, Chapman N R. Matched field inversion for geoacoustic model parameters using adaptive simulated annealing[J]. IEEE J. Oceanic Eng, 1993, 18(3): 224-231.

[3] Tolstoy A, Chapman N R, Brooke G. Workshop '97: Benchmarking for geoacoustic inversion in shallow water[J].J. Comp. Acoust, 1988, 6(1-2): 1-28.

[4] 康立山, 谢云, 尤矢勇, 等. 非数值并行算法——模拟退火算法(第一册)[M]. 北京: 科学出版社, 1998.

KANG Lishan, XIE Yun, YOU Shiyong, et alNonnumeric parallel algorithm: simulated annealing(volume one)[M]. Beijing: Science Press, 1998.

[5] 张彤, 王宏伟, 王子才. 变尺度混沌优化方法及其应用[J]. 控制与决策, 1999, 14(3): 285-288.

ZHANG Tong, WANG Hongwei, WANG Zicai, Mutative scale chaos optimization algorithm and it’s application[J]. Control and Decision, 1999, 14(3): 285-288.

[6] 陈炳瑞, 杨成祥, 冯夏亭, 等. 自适应混沌遗传算法及其参数敏感性分析[J]. 东北大学学报: 自然科学版, 2006, 27(6): 689-693.

CHEN Bingrui, YANG Chengxiang, FENG Xiating, et al. Self-Adapting Chaos-Genetic Hybrid Algorithm and Sensitivity Analysis of Its Parameters[J]. Journal of Northeastern University: Natural Science, 2006, 27(6): 689- 693.

[7] 李敏强, 寇纪松, 林丹, 等. 遗传算法的基本理论与应用[M]. 北京: 科学出版社, 2002.

LI MinQiang, KOU Jisong, LIN Dan, et alThe basic theory and application of genetic algorithm[M]. Beijing: Science Press, 2002.

[8] 田东平, 迟洪钦. 混合遗传算法与模拟退火法[J]. 计算机工程与应用, 2006, 42(22): 63-65.

TIAN Dongping, CHI Hongqin, Hybrid genetic algorithm and simulated annealing[J]. Computer Engineering and Application, 2006, 42(22): 63-65.

[9] Miller J F, Wolf S N. Modal acoustic transmission loss(MOATL): A transmission-loss computer program using a normal-mode model of the acoustic field in the ocean[M]. Washington, DC: Naval Research Laboratory, 1980.

A new genetic algorithm for matched-field inversion

ZHANG Xue-lei, FENG Jie

(The No.3 Research Institute of China Electronic Technology Group Corporation, Beijing 100015,China)

When approaching the global optimal solution, some shortcomings of the genetic algorithm, such as slow search speed, premature convergence, quick reduction of the diversity of individuals, and even getting into the trouble for local optimal solution, are highlighted. By introducing the simulated annealing factor, chaos factor and diversity measure factor into the genetic algorithm, the original shortcomings,such as the premature convergence and the poor local search capability, are greatly overcome, and meanwhile, the original powerful global search capability of genetic algorithm is maintained. So the hybrid genetic algorithm improved by all the measures can better converge at its global optimal value.

matched-field inversion; genetic algorithm; simulated annealing; Chaos;diversity measure

TP3

A

1000-3630(2015)-05-0462-05

10.16300/j.cnki.1000-3630.2015.05.015

2014-11-25;

2015-01-14

张学磊(1981－), 男, 山东潍坊人, 博士, 高级工程师, 研究方向为水声信号处理。

张学磊, E-mail: jonseray@163.com