水下目标回波的块信号稀疏分解方法

孙同晶，高恩伟，陈华杰



水下目标回波的块信号稀疏分解方法

孙同晶，高恩伟，陈华杰

(杭州电子科技大学通信信息传输与融合技术国防重点学科实验室，浙江杭州 310018)

基于匹配追踪的稀疏分解方法原理简单，在工程实际中应用广泛，但其计算量大，重构精度也不够理想。针对此问题，利用水下目标回波信号的块稀疏特性，提出了水下目标回波的块信号稀疏分解方法。首先基于水下目标回波和块稀疏信号的基本理论，结合回波信号仿真结果，分析了水下目标回波信号的块稀疏特性；然后，充分考虑回波信号本身的稀疏结构，利用信号分块和原子分块的思想，针对水下目标回波提出了块信号的稀疏分解和块匹配追踪重构算法，并从理论上对其计算复杂度进行了分析；最后，采用仿真实验的方式，与传统方法进行对比。结果表明，该方法大大减少了计算量，提高了重构精度。

块信号；目标回波；稀疏分解；匹配追踪；信号重构

0 引言

稀疏分解方法把信号分解成若干个基本信号单元的线性组合形式来简洁地表示原信号，凭借大量冗余原子可以更加灵活、简洁地实现信号的最稀疏表示。由于信号的稀疏表示能在一定程度上自然地贴近信号的本质特征，因此受到了研究者的广泛关注，并且在很多领域都得到了重要的应用，如语音信号处理、雷达探测和识别、超声成像等[1-3]。稀疏表示和重构算法主要包括贪婪追踪算法、凸松弛算法以及一些组合算法[4]。其中匹配追踪(Matching Pursuit, MP)方法是基于不断迭代的贪婪算法，MP算法原理简单，便于理解，是应用最为广泛的稀疏分解算法之一。但传统MP算法计算量较大，计算速度慢，其主要原因在于：一方面，算法所需的原子库必须是过完备的，从中选择匹配原子的工作量巨大，导致稀疏分解的计算量增大；另一方面，目前常用的快速算法[5]和智能算法[6,7]适用于一般意义上稀疏的信号，很少或没有考虑信号本身固有的结构特性。近期的研究[8-10]为克服传统算法计算量偏大的缺陷，针对一种典型稀疏信号——块稀疏信号(Block–sparse Signal)将稀疏分解和信号重构算法与信号特征相结合，进行了优化，并提出了多种改进算法[11-13]，研究结果表明此类算法较传统意义下的稀疏重构算法有更好的效果，但要求将信号的块稀疏度作为先验知识，因此必须结合实际需求背景才能获得更有效而实用的算法。

本文从待处理信号本身固有的结构特性，以降低计算复杂度、提高重构精度为目的，分析了水下目标回波信号的块稀疏特性，将分块思想与匹配追踪算法相结合，提出了适用于水下目标回波信号的块信号稀疏分解方法。

1 水下目标回波和块稀疏信号

1.1 水下目标回波模型

水下目标回波信号是水下目标受入射信号激励下的响应，从数学上来说，是入射信号和目标传递函数的卷积。在高频窄脉冲入射信号的激励下，任何一个复杂目标的回波都是由若干个子回波叠加而成的，其中的子回波可以看作是从某个散射点出发的波，这个散射点就是目标的一个亮点，它可以是真实的亮点，也可以是某个等效的亮点[14,15]。因此，在高频脉冲的激励下，任何一个复杂目标都可以等效成若干个散射亮点的组合，每个散射亮点将产生一个亮点回波，复杂目标所产生的总回波即是这些亮点回波相干叠加的结果。

亮点对回波的贡献主要可用幅度因子、时延和相位跳变三个参量进行描述。设频率为的波沿方向入射到目标上，则单个亮点的传递函数可以写成[15]

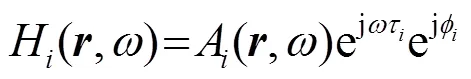
根据线性叠加原理，将目标等效为个亮点的叠加，总的传递函数可以表示为

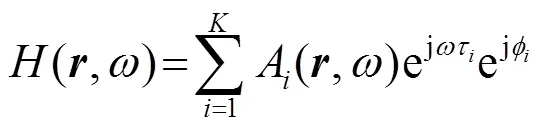
假设回波亮点为固定亮点，回波信号中包括个子回波。根据回波信号的亮点模型(不考虑相位因子的影响)，回波信号可以表示为个子回波的线性叠加，即

1.2 块稀疏信号

如果信号是稀疏的或可压缩的，则存在一组稀疏化基使得可以表示为

块稀疏信号指的是在普通稀疏信号的基础上限定了分块稀疏的特性，即信号的零值和非零值的分布呈现簇类特性，非零值只在某些特定的分块位置上出现，具体形式定义如下：

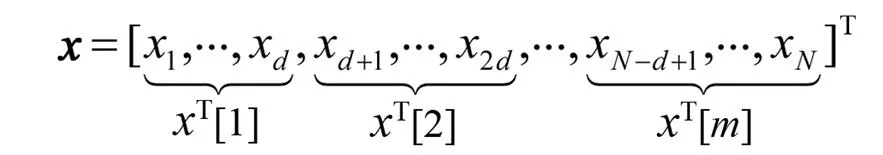
1.3 水下目标回波的块稀疏特性

由水下目标回波的亮点模型可知，一个回波由若干个亮点构成，那么每个亮点即是回波信号的一个“块”，信号的零值和非零值的分布呈现簇类特性，非零值成块出现，因此，水下回波信号具有块稀疏特性。

从回波仿真结果可以看出，不论是三亮点回波还是五亮点回波，信号只在脉冲持续时间内有值，其它时间范围没有值，即零值和非零值成块出现，呈现块稀疏特性，因此在信号的稀疏分解过程中可以充分利用其块稀疏特性。

2 块信号稀疏分解方法

2.1 块信号的稀疏分解

稀疏分解根据信号固有特点选择展开函数，从过完备原子库中找出具有最佳线性组合的项原子来表示一个信号，用较少的展开函数就可以表示出信号的基本特征，进而达到信号的稀疏逼近(或称非线性逼近)的目的。

块稀疏信号经过稀疏分解后的系数具有块稀疏特性，用稀疏分解的矩阵形式表示如下

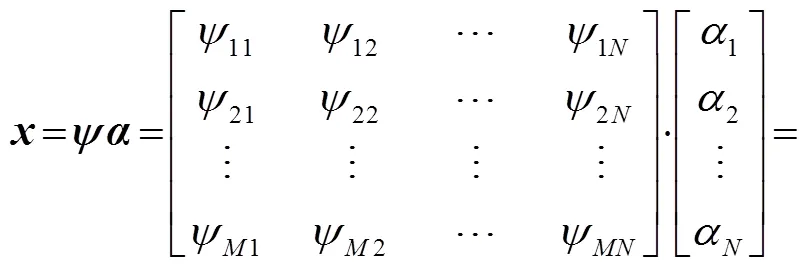
2.2 块信号匹配追踪重构方法

匹配追踪算法采用贪婪迭代的方法，从过完备原子库中选择与信号最相关的原子，并且从信号中减去其在该原子上的投影，得到一个残差信号。然后继续选择与残差信号最相关的原子，并进行相应操作。通过此过程的迭代，直到残差信号的能量小于给定的阈值或者算法达到其它终止条件。MP算法采用逐步近似来求得信号的稀疏表达式，是一种自适应的信号稀疏分解算法，原理简单，在解决实际问题时得到了广泛的应用，但其存在的主要问题在于其计算量较大，重构精度也还有待提高。针对水下回波信号的块稀疏特性，提出块信号匹配追踪(Block-signal Matching Pursuit, BMP)算法，它与传统匹配追踪方法的最大不同在于，利用原子子块中每个原子与当前残差的内积模的均值来选择相关性最大的原子子块，每次迭代找到的不再是一个原子，而是一个原子子块，充分考虑了回波信号本身的稀疏结构，大大减少了计算量，提高了重构精度。

BMP算法流程如下：

(2) 原子块选择。在第次迭代时，选择与残差内积值最大的块索引号：

(3) 更新支撑块集(所选择的与信号最匹配的原子子块集合)和残差：

具体算法流程如图3所示。从图3可以看出BMP算法与传统算法的差别在于三个步骤，即最大相关性计算、支撑块集更新和残差更新。算法在每次迭代中选择一个相关性最大即最匹配的原子块归入支撑块集，对于稀疏度为的块稀疏信号，进行次迭代过程找到整个信号的支撑块集，再通过伪逆运算重构源信号。

3 面向水下回波的块信号稀疏分解 和重构

3.1 算法仿真及重构精度分析

为了验证本文提出的块信号稀疏分解和重构方法，基于三亮点回波信号仿真结果，分别采用块分解方法和传统方法对其进行分解和重构，并将其结果进行比较，如图4和图5所示。图4(a)是待重构的原始信号，图4(b)是传统方法重构结果，图4(c)是块方法重构结果；图5中的两个图分别是两种方法所产生的残差信号。从图4和图5可以明显看出，块方法的重构精度明显提高，残差较传统方法降低了很多。

水下环境复杂，在实际测试中很难获得干净的信号，而通常夹杂着许多噪声。为了验证本文方法的抗噪性能，利用信噪比为-5 dB的含噪信号作为待分解信号，仍采用两种方法对其进行重构，并对比其重构结果和残差信号，如图6和图7所示。图6(a)是待重构的信噪比为-5 dB的原始信号，图6(b)是传统方法重构结果，图6(c)是块方法重构结果；图7中的两个图分别是两种方法所产生的残差信号。从图6和图7可以明显看出稀疏分解方法的抗噪能力，本文提出的块方法在抗噪方面的性能明显优于传统方法。

3.2 计算复杂度分析

在信号稀疏分解和重构过程中，计算复杂度(计算量)取决于信号长度、字典大小、块大小等因素。对于信号长度为，字典行数为、列数为的块稀疏信号，在单个原子搜索与迭代过程中的计算量与搜索子块完全相同，并不考虑伪逆运算时间的情况下，块稀疏算法每次迭代找到一个原子子块，与传统算法每次迭代只找到一个原子相比较，块稀疏算法的匹配速率明显提高，在相同的字典维数时，块稀疏算法的计算复杂度降低了倍。以3.1节的仿真实例为例，比较两种算法的计算效率：在3.1节的实例中，信号长度为0.1 s，即个样本点，脉冲宽度为0.01 s，即，分块数，行数，采用传统匹配追踪方法其计算量级为，而×；采用块信号匹配追踪方法，其计算量级为，而×。显然，块稀疏算法较传统算法的计算复杂度降低了倍。

4 结论

本文针对匹配追踪的稀疏分解方法计算量大，重构精度不够理想的问题，面向窄脉冲入射、亮点可分离的水下目标回波信号，采用信号分块和字典分块的思想，将信号的块稀疏特性融入稀疏分解和重构过程，提出了面向水下目标回波信号的块稀疏分解和块匹配追踪重构方法，并采用理论分析和仿真实验的方式证实了该方法在减少计算量和提高重构精度方面的性能。

对于实际目标回波信号，分块特性与入射脉宽和接收角度等因素有关，脉宽变宽或接收角度变化，有些亮点就会相互叠加产生干涉，产生非规则块状信号，针对这些问题，还需要在本文方法的基础上开展进一步的深入研究。

[1] 张弓, 杨萌, 张劲东, 等. 压缩感知在雷达目标探测与识别中的研究进展[J]. 数据采集与处理, 2012, 27(1): 1-12.

ZHANG Gong, YANG Meng, ZHANG Jin-dong, et al. Advances in Theory and Application of Compressed Sensing in Radar Target Detection and Recognition[J]. Journal of Data Acquisition and Processing, 2012, 27(1): 1-12.

[2] 张长青, 陈砚圃. 离散余弦小波包变换及语音信号压缩感知[J]. 声学技术, 2014, 33(1): 35-40.

ZHANG Changqing, CHEN Yanpu. Discrete cosine wavelet packet transform and compressed sensing for speech signal[J]. Technical Acoustics, 2014, 33(1): 35-40.

[3] 吕燚, 吴文焘, 李平. 压缩感知在医学超声成像中的仿真应用研究[J]. 声学技术, 2013, 32(2): 106-110.

LÜ Yi, WU Wentao, LI Ping. Simulation of the application of compressive sensing to medical ultrasound imaging[J]. Technical Acoustics, 2013, 32(2): 106-110.

[4] 康春玉. 压缩感知理论及其在水声中的应用[J]. 声学技术, 2013, 32(4): 412-415.

KANG Chunyu, Compressed sensing theory and its application in underwater acoustics[J]. Technical Acoustics, 2013, 32(4): 412-415.

[5] 刘浩, 潘炜. 基于FHT的实信号稀疏分解快速算法[J]. 西南交通大学学报, 2009, 44(1): 45-48.

LIU Hao, PAN Wei. Fast Algorithm for real signal sparse Decomposition Based on FHT[J]. Journal of Southwest Jiaotong university, 2009, 44(1): 45-48.

[6] 舒维杰, 袁志刚, 尹忠科. 利用人工鱼群算法基于MP的信号稀疏分解[J]. 计算机应用研究, 2009, 26(1): 66-73.

SHU Weijie, YUAN Zhigang, YIN Zhongke. Signal MP-based sparse decomposition with artificial fish swam algorithm[J]. Application Research of Computers, 2009, 26(1): 66-73.

[7] 袁志刚, 舒维杰, 尹忠科. 利用禁忌遗传和原子特性实现信号稀疏分解[J]. 计算机工程与应用, 2009, 45(11): 142-144.

YUAN Zhigang, SHU Weijie, YING Zhongke. Signal sparse decomposition based on TS and GA and atom property[J]. Computer Engineering and Applications, 2009, 45(11): 142-144.

[8] Baraniuk R G, Cevher V, Duarte M F, et al. Model based compressive sensing[J]. IEEE Trans on Information Theory, 2010, 56(4): 1982-2001.

[9] Eldar Y C, Mishali M. Robust recovery of signals from a structured union of subspaces[J]. IEEE Trans on Information Theory, 2009, 55(11): 5302-5316.

[10] Eldar Y C, Kuppinger P, Bolcskei H. Compressed sensing of block-sparse signals: uncertainty relations and efficient recovery[J]. IEEE Trans on Signal Processing, 2010, 58(6): 3042-3054.

[11] 庄哲民, 吴力科, 李芬兰, 等. 基于块稀疏信号的正则化自适应压缩感知算法[J]. 吉林大学学报, 2014, 44(1): 259-263.

ZHUANG Zhemin, WU Li-ke, LI Fen-lan, et al. Regularized adaptive matching pursuit algorithm of compressive sensing based on block sparsity signal[J]. Journal of Jilin University, 2014, 44(1): 259-263.

[12] 徐燕, 邱晓辉. 采用正交多项匹配的块稀疏信号重构算法[J]. 信号处理, 2014, 30(6): 706-711.

XU Yan, QIU Xiaohui. Block-sparse signals recovery using orthogonal multimatching[J]. Journal of Signal Processing, 2014, 30(6): 706-711.

[13] 田鹏武, 康荣宗, 于宏毅. 非均匀块稀疏信号的压缩采样与盲重构算法[J]. 电子与信息学报, 2013, 35(2): 445-450.

TIAN Pengwu, KANG Rongzong, YU Hongyi. Compressive sampling of non-uniform block sparse signals and the blind recovery algorithm[J] Journal of Electronics & Information Technology, 2013, 35(2): 445-450.

[14] 李昌志, 田杰, 张扬帆, 等. 基于亮点模型的典型水下目标回波信号仿真[J]. 应用声学, 2010, 29(3): 196-201.

LI Changzhi, TIAN Jie, ZHANG Yangfan, et al. Simulation of echoes from underwater target based on highlight model[J]. Applied Acoustics, 2010, 29(3): 196-201.

[15] 汤渭霖. 声呐目标回波的亮点模型[J]. 声学学报, 1994, 19(2): 92-100.

TANG Weilin. Highlight model of echoes from sonar targets[J]. Acta Acoustica, 1994, 19(2): 92-100.

Block-signal sparse decomposition method for underwater echo

SUN Tong-jing, GAOEn-wei, CHENHua-jie

(Fundamental Science on Communication Information Transmission and Fusion Technology Laboratory,Hangzhou Dianzi University, Hangzhou 310018, Zhejiang, China)

The principle of the sparsedecomposition method based onmatching pursuitissimple,and it is widely usedin the practical engineering.But calculation amount andreconstruction accuracyis not satisfactory.To solve the problem, blocksignalsparse decomposition methodforunderwater echo is proposed based onblock sparse characteristics of echo signal.At first, block sparse characteristics of underwater acoustic echo signal is analyzed by combining thebasic theory ofecho andblock sparse signalwith echo signalsimulation results.And then,considering thesparse structure ofthe echo signalitself,and using the idea ofatomicblockandsignal block, algorithms of block sparse decompositionand block matchingpursuit for underwater echo signal are proposed,andcomputational complexity is analyzed from the theory. At last,by thesimulationexperiment, the methodin this paper is comparedwith traditionalmethod,and the results show thatthe presented method in this paper can greatly reduce theamount of computation,and improve the accuracy of the reconstruction.

block-signal; target echo; sparse composition; matching pursuit; signal recovery

TN911.7

A

1000-3630(2015)-05-0457-05

10.16300/j.cnki.1000-3630.2015.05.014

2015-04-08;

2015-07-09

孙同晶(1978－), 女, 吉林公主岭人, 博士, 高级工程师,研究方向为水声信号处理和信息融合。

孙同晶, E-mail: stj@hdu.edu.cn