非紧系统的次可加拓扑压

杨宇，张秀芬

（西北大学数学学院，陕西 西安　710127）

非紧系统的次可加拓扑压

杨宇，张秀芬

（西北大学数学学院，陕西 西安710127）

利用逆紧映射、容许覆盖等概念，将紧系统上的次可加拓扑压推广到非紧系统上，给出了次可加拓扑压的定义，并讨论了非紧系统上次可加拓扑压的性质.

非紧系统；逆紧映射；容许覆盖；次可加拓扑压

1　引言

在测度论中，古典的Carathéodory构造是由Carathéodory在文献［1］中给出的.文献［2］介绍了一种新的构造，这种构造是古典Carathéodory构造的推广，它引出了一些具有维数性质的量，例如Hausdorff维数、拓扑熵等，称这种构造为Carathéodory-Pesin结构（简称为C-P结构），它是研究维数论和动力系统的重要工具.此外，文献［3］利用C-P结构给出了紧系统上不可加拓扑压的维数定义.文献［4］利用逆紧映射、容许覆盖等概念以及C-P结构给出了非紧系统上拓扑熵的定义.受文献［3-4］的启发，本文利用文献［4］的方法，将紧系统上的次可加拓扑压推广到非紧系统上，同时给出了拓扑压、下容量拓扑压和上容量拓扑压的定义，并介绍了非紧系统上次可加拓扑压的性质，如：拓扑压的维数性质、拓扑压关于半范数连续的性质以及拓扑压的一些等价刻画等.

2　预备知识

本文恒设（X，d）是局部紧的可分度量空间.

定义2.1［5］设X是拓扑空间.称f：X→X是逆紧映射，如果f是连续的，并且任意紧集在f下的原像是紧的.

定义2.2［5］称开集U为容许开集，如果U的闭包或补集是紧的.

定义2.3［5］称X的开覆盖U为容许覆盖，如果U有限并且对任意A∈U，A是容许开集.

定义 2.4［5］称度量d是容许的，如果满足下列条件：

（1）如果对任意δ∈（a，b）（0＜a＜b），Uδ=｛B（x1，δ），···，B（xk，δ）｝是X的开覆盖（B（x，δ）表示以x为球心，以δ为半径的开球），那么存在δε∈（a，b），使得Uδε是容许覆盖.

（2）X的每个容许覆盖都有Lebesgue数.

定义2.5［6］称函数列Φ=（φn）n∈N是次可加的，如果对任意m，n∈N和x∈X有

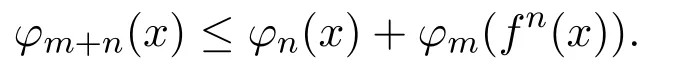
定义2.6设（X，d）是局部紧的可分度量空间，f是逆紧映射，则称（X，f）是逆紧系统.

3　非紧系统上次可加拓扑压的定义

设（X，f）为非紧的逆紧系统，对任意n∈N和X的容许覆盖U，用Wn（U）表示所有长度为n的向量U=（U1，···，Un）构成的集合，U1，···，Un∈U.对任意U∈Wn（U），记向量U的长度为m（U）.定义

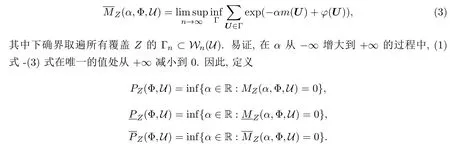
引理 3.1［4］设X是局部紧的可分度量空间，是X 的单点紧化，如果d是的某一度量限制在X上的度量，那么d是容许度量，并且对任意ε＞0，存在X的容许覆盖，使得这个覆盖的直径小于ε.

引理3.2设（X，f）为逆紧系统，对任意次可加的缓变连续函数列Φ，极限

存在.

4　非紧系统上次可加拓扑压的性质

本节介绍非紧系统上次可加拓扑压的性质.例如：拓扑压的维数性质、拓扑压关于半范数连续的性质以及拓扑压的一些等价刻画.

定理4.1设（X，f）为逆紧系统，Φ是次可加的连续函数列，那么关于拓扑压有以下性质：

定理4.2设（X，f）为逆紧系统，Φ是次可加的连续函数列，那么关于上容量拓扑压、下容量拓扑压有以下性质：

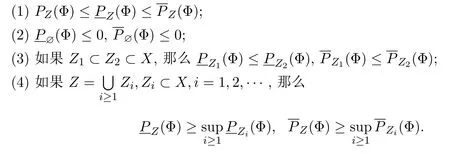
定理4.1和定理4.2的证明可参考文献［2］.

定义X上函数列Φ空间中的一个半范数

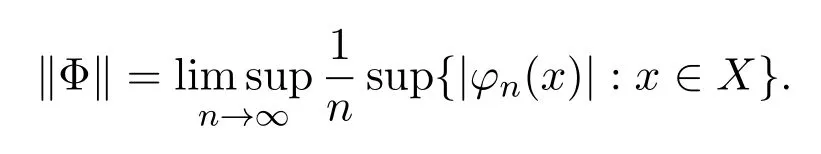
下面的定理表明拓扑压关于这个半范数是连续的.

定理4.3设（X，f）为逆紧系统，对任意次可加的缓变连续函数列Φ=（φn）n∈N和Ψ=（ψn）n∈N，下面的性质成立：

（1）当n充分大时，如果φn≤ψn，那么

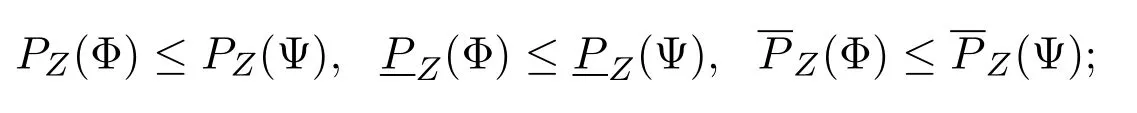
（2）如果∥Φ∥＜∞，∥Ψ∥＜∞，那么

定理4.4设（X，f）为逆紧系统，Φ是次可加的连续函数列.对任意n∈N，定义

其中下确界取遍所有覆盖Z的Γn⊂Wn（U）.那么

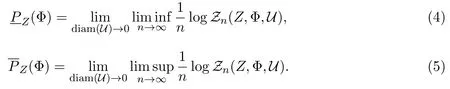
定理4.5设（X，f）为逆紧系统，Φ是次可加的有界连续函数列.

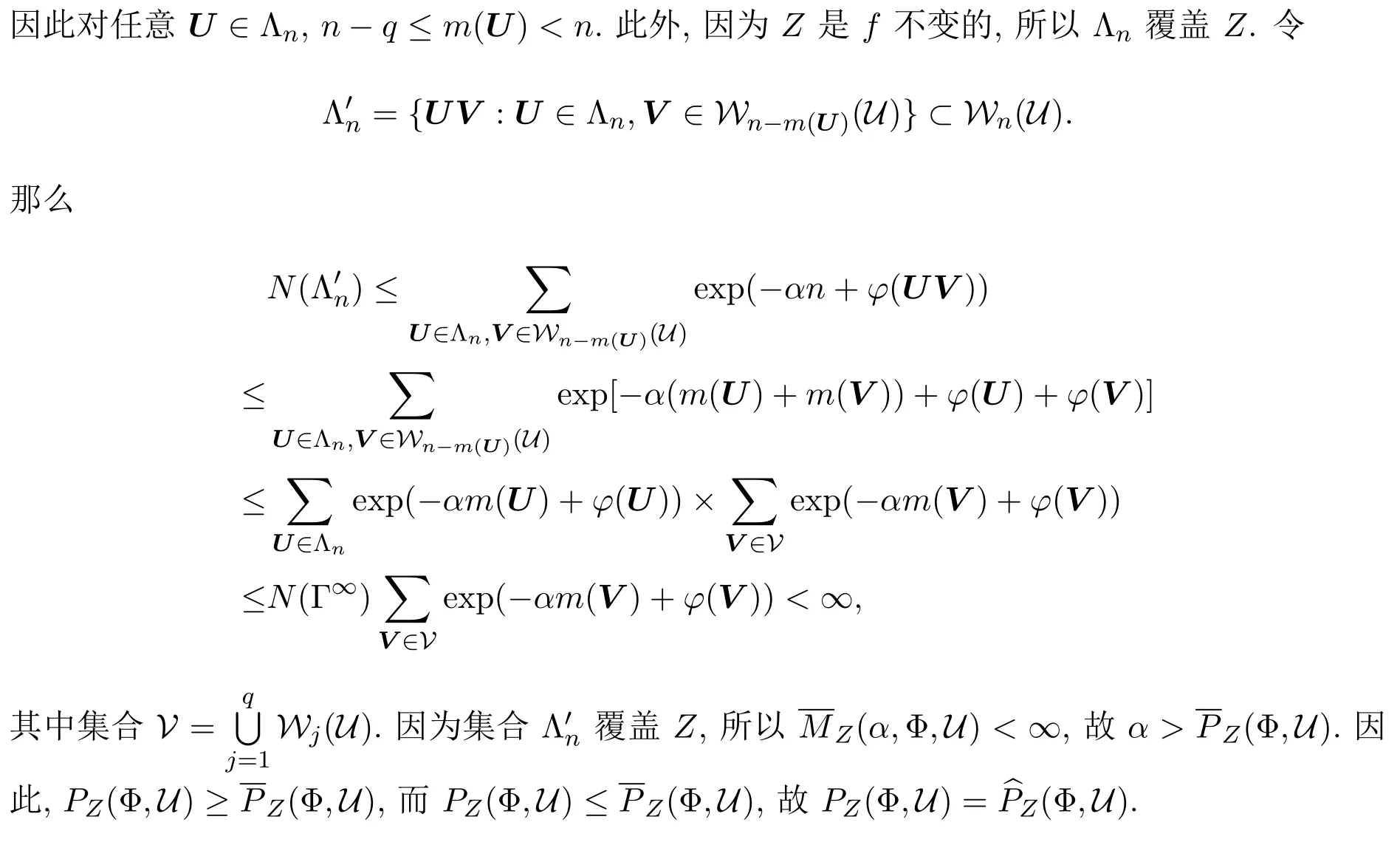
［1］Carathéodory C.Über das lineare mass［J］.Göttingen Nachr.，1914，1914：406-426.

［2］Pesin Y.Dimension Theory in Dynamical Systems［M］.Chicago：the University of Chicago Press，1997.

［3］Barreira L.A non-additive thermodynamic formalism and applications to dimension theory of hyperbolic dynamical systems［J］.Ergod.Theory and Dyn.Syst.，1996，16：871-828.

［4］Ma Dongkui，Cai Bin.Topological entropy of proper map［J］.Taiwanese Journal of Mathematics，2014，18（4）：1219-1241.

［5］Patrão M.Entropy and its variational principle for non-compact metric spaces［J］.Ergodic Theory Dynam.Systems，2010，30：1529-1542.

［6］Barreira L.Thermodynamic Formalism and Applications to Dimension Theory［M］.Basel：Birkhäuser，2011.

［7］廖公夫，王立冬，范钦杰.映射迭代与混沌动力系统［M］.北京：科学出版社，2013.

The subadditive topological pressure of a noncompact system

Yang Yu，Zhang Xiufen

（College of Mathematics，Northwest University，Xi′an710127，China）

By the notions of proper mapping，admissible cover and so on，subadditive topological pressure of the compact system is generalized to the noncompact system.The notion of subadditive topological pressure is given and some properties of subadditive topological pressure of the noncompact system are studied.

the noncompact system，proper mapping，admissible cover，subadditive topological pressure

O189.1

A

1008-5513（2015）03-0265-08

10.3969/j.issn.1008-5513.2015.03.007

2015-01-16.

国家自然科学基金（11301417）.

杨宇（1991-），硕士生，研究方向：拓扑动力系统及其遍历理论.

2010 MSC：54A10