关于子基的连通性的注记
2015-10-14刘德金
刘德金
(德州学院数学科学学院,山东 德州 253023)
关于子基的连通性的注记
刘德金
(德州学院数学科学学院,山东 德州253023)
在粗糙集理论研究中,覆盖方法的应用越来越受重视,其中最重要的概念是最近引进的拓扑空间的子集关于子基的内部和闭包以及由它们导入的关于子基的开集、闭集.对由它们导入的拓扑空间关于子基的隔离子集、连通性作进一步研究,所得性质是一般拓扑空间中隔离子集和连通性相应结果的推广.
子基;关于子基的开集;关于子基的闭集;关于子基的隔离子集;关于子基的连通性
1 引言
在粗糙集理论的研究中,粗糙集与拓扑空间关系的研究是一个重要内容.继文献[1-3]研究粗糙集与拓扑空间的关系之后,文献[4]将粗糙集理论推广到覆盖广义粗糙集理论,随后不少学者对覆盖广义粗糙集理论进行了深入的研究[5-8].为了使粗糙集理论和覆盖广义粗糙集理论中的下近似集和上近似集都能分别地对应于某一拓扑空间的子集的某种内部和闭包,文献[9]定义了拓扑空间的子集关于子基的内部和闭包,在此基础上文献[10]研究了拓扑空间的子集关于子基的连通性概念,得到许多重要结果.本文对文献[10]给出的关于子基的隔离子集和关于子基的连通性的概念作进一步研究,得到一些重要的结论,是对拓扑空间关于子基的连通性的重要补充,也是一般拓扑空间中隔离子集、连通性相应结论的推广.文中关于子基的内部、闭包、开集、闭集、隔离子集、连通空间、连通子集等概念均见文献[9-10],在此不再赘述.
2 预备知识
设X为非空集合,给定X上的拓扑T,若β是T的子基,则该拓扑空间记为(X,T,β).X的子集A的补集记为~A.
引理2.1设(X,T,β)是拓扑空间,Y为X的子集,则T|Y是Y的拓扑,β|Y是Y的子基,并且对Y的任何子集A,有

证明若T为X的拓扑,β为T的子基,由文献[11]知T|Y是Y的拓扑,β|Y是Y的子基.
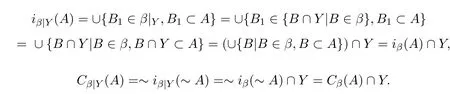
引理2.2设(X,T,β)是拓扑空间,则对任意X的子集A,iβ(A)是β开集,Cβ(A)是β闭集.
证明由文献[9]中命题2.1(9)、定义3.1和定理3.6可证.
引理2.3设(X,T,β)是拓扑空间,(Y,T|Y,β|Y)是其子空间,A1⊂Y.则A1是Y的β|Y开集当且仅当存在X的β开集A,使得A1=A∩Y.
证明由引理2.1和引理2.2可知,命题成立.
引理2.4设(X,T,β)是拓扑空间,(Y,T|Y,β|Y)是其子空间.则Y的子集A、B是Y 的β|Y隔离子集当且仅当A、B是X的隔离子集.
证明由文献[9]中定理1.8的证明可知,结论成立.
引理2.5[10]设(X,T,β)是拓扑空间.则下列条件等价:
(1)X是β不连通空间;
(2)X中存在两个非空的β开集A与B,使得X=A∪B,A∩B=∅;
(3)X中存在两个非空的β闭集A与B,使得X=A∪B,A∩B=∅;
(4)X中存在一个既是β开集又是β闭集的非空真子集.
引理2.6[10]设(X,T,β)是拓扑空间,C为X的β连通分支.则
(1)若Y为X的β连通子集,且Y∩C≠∅,则Y⊂C;
(2)C是X的β连通子集;
(3)C是X的β闭集.
引理2.7[10]设(X,T,β)是拓扑空间,且Y⊂Z⊂X,则Y为X的β连通子集当且仅当Y为X的子空间Z的β|Z连通子集.
3 主要结果
定理3.1设(X,T,β)是拓扑空间,A与B是X的β隔离子集,如果A1⊂A,B1⊂B,则A1与B1也是X的β隔离子集.

定理3.2设A与B是拓扑空间(X,T,β)的β隔离子集.如果A∪B是X的β开集(β闭集),则A与B也都是X的β开集(β闭集).

设A∪B是X的β闭集,由引理2.2得Cβ(A∪B)=A∪B,则Cβ(A)⊂Cβ(A∪B)=A∪B,因为A与B是X的β隔离子集,所以Cβ(A)∩B=∅,所以Cβ(A)⊂A,于是得Cβ(A)=A,由引理2.2知A是X的β闭集.同理可知B是X的β闭集.
定理3.3设A是拓扑空间(X,T,β)的β连通子集.B既是X的一个β开集,又是X的一个β闭集.如果则A⊂B.
证明设C=~B,则C也是既β开又β闭的子集,且B和C是X的β隔离子集.因为A⊂B∪C=X,所以由文献[10]中定理1.10知,A⊂B或A⊂C.因为所以A⊂B.
定理3.4设Y是拓扑空间(X,T,β)的β连通子集.如果A与B是X的两个不交的β开集(β闭集),使得Y⊂A∪B,则或者Y⊂A,或者Y⊂B.
证明设A与B是X的两个不交的β开集,即A与B是β开集,且A∩B=∅,这说明A∩Cβ(B)=∅,Cβ(A)∩B=∅.所以A与B是X的两个β隔离子集.因为Y⊂A∪B,Y 是β连通子集,所以由文献[10]中定理1.10知,或者Y⊂A,或者Y⊂B.
定理3.5设A是β连通空间(X,T,β)的一个非空真子集,则

定理3.6设C是β连通空间(X,T,β)的一个β连通子集.若C是β开集,又是β闭集,则C是X的β连通分支.
证明设Y是包含C的β连通分支,则C⊂Y,且C是Y的β|Y开集,也是Y的β|Y闭集,由引理2.6知Y是X的β连通子集,即Y是β|Y连通的,因此Y没有既β|Y开又β|Y闭的真子集,所以C=Y,即C是X的β连通分支.
定理3.7 设(X,T,β)是拓扑空间,E⊂G⊂X,E是X的β开集,且E是G的β|G连通分支.则bβ(E)⊂bβ(G).

注3.1由引理2.7可知,定理3.7中的条件“E是G的β|G连通分支”换为“E是X 的β连通分支”命题仍然成立.
定理3.8设(X,T,β)是拓扑空间,G⊂X,G是X的β连通的子集且是β开集,则G 是X-bβ(G)中的一个β连通分支.

定理 3.9设X是拓扑空间,β1、β是X的两个子基,β1⊂β.如果(X,T,β)是β连通的,则(X,T1,β1)是β1连通的.
证明反证法.假设(X,T1,β1)不是β1连通空间,则由引理2.5知,存在两个非空β1开集A,B使得X=A∪B,A∩B=∅.因为β1⊂β,所以A,B也是两个非空的β开集,使得X=A∪B,A∩B=∅,又由引理2.5知,(X,T,β)不是β连通的,与条件矛盾.所以(X,T1,β1)是β1连通的.
定理3.10设(X,T,β)是拓扑空间,Y是X的一个子集.则Y是X的不连通子集的充分必要条件是存在X的β开集(β闭集)A和B,使得Y⊂A∪B,A∩B⊂X-Y ,和

“⇐”设存在X的β开集(β闭集)A和B使得Y⊂A∪B,A∩B⊂X-Y,和则Y=(A∩Y)∪(B∩Y),记A1=A∩Y,B1=B∩Y,则A1和B1是Y的非空的β|Y开集(β|Y闭集),且Y=A1∪B1,A1∩B1=(A∩B)∩Y=∅.所以Y是X的β不连通子集.
定理3.11设Y和Z是拓扑空间(X,T,β)的子集.若Y和Z同时为X的β闭集(β开集),则Y-Z和Z-Y是X的β隔离子集.

定理3.12设Y是拓扑空间(X,T,β)的子集.Cβ(Y)是X的一个不连通子集,则X中存在两个非空集合A和B使得Y⊂A∪B,Cβ(A)∩Cβ(B)=∅,Y∩A≠∅和Y∩B≠∅成立.
证明设Cβ(Y)是X的一个不连通子集,由文献[10]中定理1.8知,存在X的非空β隔离子集A和B使得Cβ(Y)=A∩B.由引理2.2知,A∩B是β闭集,又由定理3.2知,A 和B是X的β闭集,所以Cβ(A)=A,Cβ(B)=B,因为A和B是X的β隔离子集,所以A∩B=∅,从而Cβ(A)∩Cβ(B)=∅.显然Cβ(Y)∩A≠∅和Cβ(Y)∩B≠∅.若Y∩A=∅,则由Y⊂Cβ(Y)=A∪B得Y⊂B,故Cβ(Y)⊂Cβ(B),这与Cβ(Y)∩A≠∅,A∩Cβ(B)=∅矛盾,所以Y∩A≠∅.同理Y∩B≠∅.
由于当β是一个拓扑空间的基时,β开集与开集等价;β闭集与闭集等价,β隔离子集与隔离子集等价,β连通与连通等价,β不连通与不连通等价.因此上面所得的若干结果是文献[11-12]中相应结果的推广.例如:拓扑本身是子基,所以特别地取β=T,这时定理3.11就可表述为:“设Y和Z是拓扑空间(X,T)的子集.若Y和Z同时为X的闭集(开集),则Y-Z和Z-Y是X的隔离子集.”这正是文献[11]中48页上的重要定理.
[1]Yao Y Y.Relationl interpretations of neighborhood operators and rough set approximation operators[J].Information Science,1988,111(1/4):239-259.
[2]陈德刚,张文修.粗糙集与拓扑空间[J].西安交通大学学报,2001,35:1314-1315.
[3]李进金.覆盖广义粗糙集理论中的拓扑方法[J].模式识别与人工智能,2004,17(1):7-10.
[4]Zakowski W.Approximations in the space(U,R)[J].Demonstratio Matheznatica,1983,16:761-769.
[5]Bryniaski E.A calculus of rough sets of the first order[J].Bulletin of the Polish Academy of Sciences,1989,37(16):71-77.
[6]Bonikowski Z,Bryniarski E,Wybraniec-Skardowska U.Extensions and intentions in the rough set theory[J].Information Science,1998,107:149-167.
[7]Pomykala J A.Approximation operations in approximation space[J].Bulletion of the Polish Academy of Science,1987,35(9/10):653-662.
[8]祝峰,王飞跃.关于覆盖广义粗集的一些基本结果[J].模式识别与人工智能,2002,15(1):6-12.
[9]李进金.由子基生成的内部算子和闭包算子[J].数学进展,2006,35(4):478-484.
[10]李进金.关于子基的连通性[J].数学进展,2007,36(4):421-428.
[11]熊金诚.点集拓扑讲义[M].4版.北京:高等教育出版社,2011.
[12]凯莱J L.一般拓扑学[M].北京:科学出版社,1982.
Note on connectedness relative to a subbase
Liu Dejin
(Department of Mathematics,Dezhou University,Dezhou253023,China)
Covering methods are widely used in rough set theory.The interior and the closure of a subset relative to a subbase for the topology are introduced to study the relationships between the rough sets and the topological space.This paper makes a further research on the separated subset and the connectedness relative to a subbase,and obtains some properties which generalize separated subset and the connectedness in a general topology.
subbase,the open set relative to a subbase,the close set relative to a subbase,the separated subset relative to a subbase,the connectedness relative to a subbase
O189.1;TP18
A
1008-5513(2015)03-0231-07
10.3969/j.issn.1008-5513.2015.03.002
2014-11-16.
刘德金(1957-),教授,研究方向:几何与一般拓扑学.
2000 MSC:56A10,68T01
