一类“食物有限”基于比率的Holling-Tanner离散模型的持久性
2015-10-14吴丽萍
吴丽萍
(闽江学院数学系,福建 福州 350108)
一类“食物有限”基于比率的Holling-Tanner离散模型的持久性
吴丽萍
(闽江学院数学系,福建 福州350108)
研究一类“食物有限”基于比率的Holling-Tanner离散捕食者-食饵模型.利用差分方程的不等式理论及振动理论,证明在一定条件下,该系统是持久的.
离散;食物有限;基于比率;Holling-Tanner模型;持久性
1 引言
本文研究如下“食物有限”基于比率的Holling-Tanner离散捕食者-食饵模型:

其中x(n),y(n)分别表示食饵种群和捕食者种群在第n代的种群密度,{r(n)},{K(n)},{c(n)},{b(n)},{a(n)},{s(n)},{h(n)}是非负有界序列.
基于生态学意义,本文考虑系统(1)具有正初值x(0)>0,y(0)>0的解(x(n),y(n)).易知,系统(1)具有正初值x(0)>0,y(0)>0的解是正的.
系统(1)可以看成是与如下连续模型:

对应的离散模型.文献[1]在{r(t)},{K(t)},{c(t)},{b(t)},{a(t)},{s(t)},{h(t)}都是常数的情形下,研究了系统(2)的正平衡点的局部渐近稳定性,以及正平衡点附近Hopf分支的存在性.
然而,对于生命短、世代不重叠的种群,或者是生命长、世代重叠的种群,在其数量比较少时,通常表示为差分方程[2].近年来,离散生态系统的动力学行为得到广泛研究[3-10].目前尚未有文献对系统(1)进行研究.本文利用差分方程的不等式理论及振动理论,得到保证系统(1)持久的充分性条件.
2 持久性
定义2.1如果存在常数µ和ν(0<µ<ν),使得对系统(1)的任一正解(x(n),y(n)),有

则称系统(1)是持久的.
引理2.1[3]假设{x(k)}满足x(k)>0且x(k+1)≤x(k)exp{a(k)-b(k)x(k)},k∈N,其中{a(k)}和{b(k)}是有正的上界和下界的序列,则

引理 2.2[3]假设{x(k)}满足

引理2.3 设(x(n),y(n))是系统(1)的任一正解,则



情形 2若 {x(n)}关于 K∗不振动,则存在正整数 n1,当 n>n1时,x(n)<K∗(或x(n)>K∗).

引理2.4 设(x(n),y(n))是系统(1)的任一正解,则
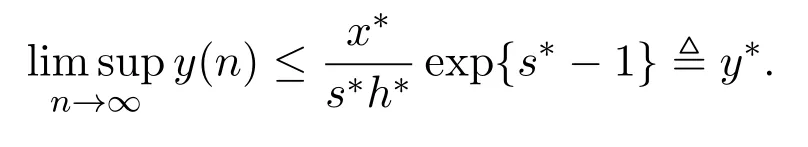

引理2.5假设(H):r∗a∗-b∗>0,成立,则对系统(1)的任一正解(x(n),y(n))有
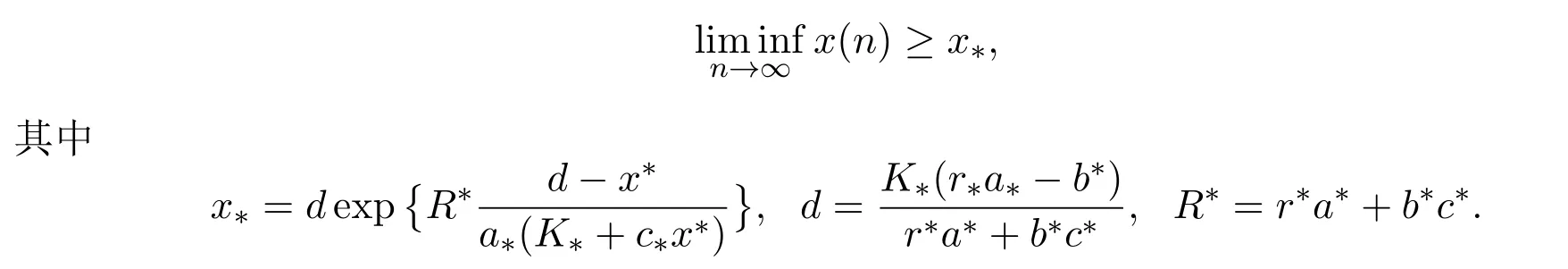


引理2.6 设(x(n),y(n))为系统(1)的任一正解,则
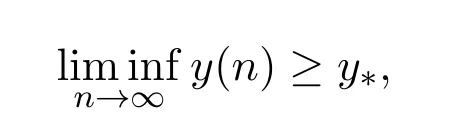
其中
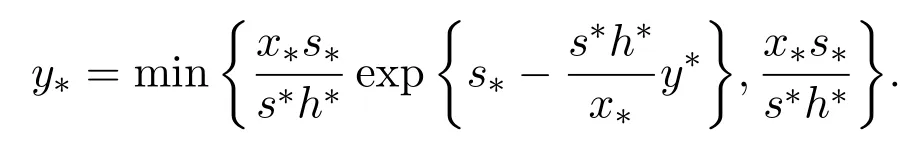

定理2.1设系统(1)满足条件(H):r∗a∗-b∗>0,则系统(1)是持久的.

注 2.1本文研究了一类“食物有限”基于比率的Holling-Tanner离散捕食者-食饵模型在一定条件下是持久的.对于该系统全局吸引性的研究比较复杂,将在后续的文章中进行研究.
[1]Yang Bo.Pattern formation in a diffusive ratio-dependent Holling-Tanner predator-prey model with Smith Growth[J].Discrete Dynamics in Nature and Society,2013,DOI:org/10.1155/2013/454209.
[2]陈兰荪,宋新宇,陆征一.数学生态学模型与研究方法[M].四川:四川科学技术出版社,2003.
[3]Chen F D.Permanence for the discrete mutualism model with time delays[J].Math.Comput.Model.,2008,47(3/4):431-435.
[4]Fan M,Wang K.Periodic solutions of a discrete time nonautonomous ratio-dependent predator-prey system[J].Math.Comput.Modelling,2002,35(9/10):951-961.
[5]Huo H F,Li W T.Stable periodic solution of the discrete periodic Leslie-Grower predator-prey model[J].Math.Comput.Model.,2004,40(3/4):261-269.
[6]Yang X T,Liu Y Q,Chen J.Uniform persistence for a discrete predator-prey system with delays[J].Appl.Math.Comput.,2011,218(4):1174-1179.
[7]梁志清.一类基于比例确定的离散系统正周期解的存在性[J].生物数学学报,2004,19(4):421-427.
[8]Teng Z D,Zhang Y,Gao S J.Permanence criteria for general delayed discrete nonautonomous n-species Kolmogorov systems and its applications[J].Comput.Math.Appl.,2010,59(2):812-828.
[9]Li Y K,Zhang T W.Permanence and almost periodic sequence solution for a discrete delay logistic equation with feedback control[J].Nonlinear Anal.RWA.,2011,12(3):1850-1864.
[10]卞继承,范志强,徐加波,等.带无穷时滞两种群Lotka-Volterra离散模型的持久性[J].纯粹数学与应用数学,2014,30(2):166-172.
Permanence for a“food-limited”ratio-dependent Holling-Tanner discrete model
Wu Liping
(Department of Mathematics,Minjiang University,Fu′zhou350108,China)
In this paper,a“food-limited”discrete ratio-dependent Holling-Tanner predator-prey model is studied.By using the theory of difference inequality and the oscillation theory of difference equation,it is showed that the system is permanence under some conditions.
discrete,food-limited,ratio-dependent response,Holling-Tanner model,permanence
O175.12
A
1008-5513(2015)03-0245-07
10.3969/j.issn.1008-5513.2015.03.004
2014-11-02.
吴丽萍(1972-),硕士,副教授,研究方向:生物数学.
2010 MSC:39A05,39A21,92D25
