高压水射流冲击破岩损伤场分析

江红祥，杜长龙，刘送永，高魁东



高压水射流冲击破岩损伤场分析

江红祥，杜长龙，刘送永，高魁东

(中国矿业大学 机电工程学院，江苏 徐州，221116)

以Johnson-Holmquist modelⅡ(JH-2)脆性材料本构模型来表征岩石的力学特性，利用光滑粒子流(SPH)和有限元(FEA)耦合算法建立高压水射流冲击破岩过程的数值模型，很好地模拟水射流损伤破岩过程中岩石失效、裂纹扩展以及不同位置岩石单元的损伤程度随时间变化的过程。此外，模拟分析射流冲击速度、入射角以及平移速度对岩石损伤场的影响。研究结果表明：岩石的损伤破坏、裂纹扩展是剪切和拉伸共同作用引起的，且近射流冲击点的损伤破坏由剪切作用主导，而放射性裂纹和层状裂纹的扩展主要由拉伸作用主导；岩石单元的损伤值随时间呈阶跃性变化，且射流冲击损伤破岩过程为微秒量级；射流冲击损伤破岩的入射角存在一个有效范围，当入射角大于70o时损伤破岩效果较好；射流冲击速度较低时以表面冲蚀岩石为主，射流冲击速度达到一定值才能使岩石损伤破坏，出现放射性裂纹和层状裂纹；射流平移速度与冲击速度相比很小，对岩石的损伤场影响不明显。

水射流；光滑粒子流；有限元；岩石损伤破坏；JH-2本构模型

高压水射流破岩技术已经在石油钻井、地下工程以及瓦斯抽放等领域得到了很好的应用[1−4]。高压水射流破岩的机理和实际物理过程非常复杂，其损伤破岩机理的研究一直都是热点和难点问题[5−6]。到目前为止，在理论和实验研究基础上主要形成了汽蚀破坏、冲击破坏、动压破坏以及水楔破坏等理论学说。高压水射流损伤破岩过程是集流体力学、岩石力学、冲击动力学及流固耦合等的多学科问题，其损伤破岩机理至今未形成较统一的学说[7]。此外，由于岩石的透明性差，难以通过实验方法来观察、研究岩石的损伤破坏过程，也不能确定是拉应力、剪应力或压应力引起的损伤破坏。目前已有很多学者对高压水射流冲击破岩过程进行数值模拟研究：廖华林等[8]利用标准−双方程模型、体积控制法、各向同性弹性力学以及有限元法建立了水射流和岩石耦合数值模型，模拟研究了不同冲击速度条件下水射流的动力学特性以及岩石内部的应力分布规律；Ni等[9]利用有限元、损伤力学以及细观力学等理论建立了水射流破岩的流固耦合模型，模拟表明射流冲击破岩存在拉伸和卸载过程；孙清德等[10]利用动态有限元法模拟了高压水射流破岩过程，认为水射流破岩的2个临界压力直接影响破岩机理，并分析了射流冲击速度、横移速度以及入射角等对破岩效率的影响规律；司鹄等[11]利用非线性动态有限元法对水射流破岩过程中岩石应力波效应进行了数值分析，表明岩石受到水射流冲击时的不稳定性是一个由强变弱的过程；刘佳亮等[7]利用拉格朗日−欧拉耦合算法对水射流冲击有围压岩石的损伤破坏过程进行了模拟，认为围压对岩石轴向的损伤演化有较大的影响；卢义玉等[12]利用光滑粒子动力学方法模拟了脉冲射流冲击不同类型岩石的应力波效应，且应力波导致不同类型岩石的破坏形式不同。以上研究在一定程度上推动了水射流破岩机理的发展，但并未深入研究水射流损伤破岩过程以及岩石损伤场的演化和裂纹扩展过程。为此，本文作者采用SPH/FEA耦合方法建立了高压水射流冲击损伤破坏岩石的过程，对岩石的损伤场演化和裂纹扩展过程进行模拟研究，并对影响岩石损伤场的因素进行数值分析，以期提高对高压水射流冲击损伤破岩过程的认识。

1 水射流冲击损伤破坏岩石数值模型

1.1 SPH/FEA耦合算法

高压水射流冲击损伤破岩过程中，高速射流出现高压和大变形问题，采用传统的拉格朗日法模拟水射流容易出现网格畸变而导致计算终止。采用欧拉−拉格朗日耦合算法虽然可以避免网格的畸变，但其需要消耗更高的计算成本[13]。SPH算法是近年发展起来的一种无网格算法，属于拉格朗日范畴，它是用粒子单元代替有限元网格，并基于空间函数和核函数将方程离散。SPH/FEA耦合算法可以很好地模拟不连续、大变形等问题，还可以克服传统有限元以及欧拉法存在的网格畸变、计算耗时以及资源占用过多等问题[14−15]。

1.1.1 SPH算法

与有限单元法相比，SPH方法的粒子单元是离散的，采用光滑长度内粒子代替了有限元法中的节点，每个粒子周围光滑长度内的粒子数量和分布是不确定的。对于任意连续光滑场函数，用()来近似某一点的场函数值，()可表述为

式中：为光滑核函数，目前最常用的光滑核函数是三次B样条曲线函数[16]；为光滑长度；和’为空间不同位置点的向量。

在式(1)的基础上，利用散度定理即可得到场函数的空间导数，进而离散化可得到

式中：m为第个SPH粒子的质量；为第个粒子的密度；为光滑长度范围内的粒子数。

通过上述过程的处理，即可用光滑核函数的场函数来近似光滑场函数的空间导数项，进而实现基本方程的离散，SPH方法离散后的Navier-Stocks方程：

1.1.2 耦合边界处理

在水射流冲击损伤破岩过程中，固体介质(岩石)的应变率要比液体介质(水)小得多。此外，由于SPH粒子单元过多会导致计算机所需要的内存过大、计算时间过长，故本文的岩石介质的应力、应变等状态参数通过有限元法来求解。由于岩石内孔隙流体与岩石耦合作用对岩石损伤破坏的影响很小[17]，可忽略不计，故本文利用节点−面接触算法定义射流与岩石界面之间的耦合：SPH粒子视作节点单元，控制参数为节点编号、质量以及空间位置，其定义为从节点；有限元法描述的岩石介质部分定义为主面。射流和岩石的应力、应变等状态参数同时求解，通过节点−面接触算法实现力的传递，且射流与岩石之间满足滑移条件：

式中：为射流和岩石接触面SPH粒子速度；为射流和岩石接触区域固体单元的速度。

1.2 材料模型

1.2.1 水射流材料模型

水射流冲击损伤破岩过程中的状态通过多项式状态方程描述。当水处于压缩状态时(≥0)，状态方程为

当水处于膨胀状态时(≤0)，状态方程为

式中：w为水压力；w为水的密度；为水压缩比；为水的内能；1，2，3，1，2，0以及1为水介质材料常数，相关参数如表1所示。

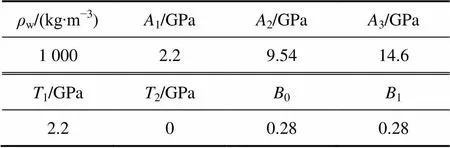
表1 水状态方程相关参数

1.2.2 岩石材料模型

岩石材料的力学特性采用JH-2本构模型描述，该模型可以很好的模拟材料的大变形、高应变率以及高压效应。材料体积应变与静水压力之间的关系用状态方程来描述，在低速冲击情况下静水压力张量较小。由于本文侧重分析射流冲击损伤破岩，而确定损伤度时需要准确的高压状态方程，因此，该情况下岩石采用3次多项式状态方程来描述。未受到冲击损伤时，JH-2本构模型中岩石的状态方程[18]：

式中：r为静水压力；1为岩石的体积模量；2和3为岩石材料常数；为岩石的体积应变。

JH-2强度模型是在引入应变率和损伤因子基础上，将材料的等效应力表示成静水压力的幂函数形式，其中规范化强度模型为

当岩石的损伤因子=0时，规范化等效应力为

当岩石的损伤因子=1时岩石完全失效，规范化等效应力为

JH-2模型中的损伤因子可表示为：

采用改进的最大主应力模型[20]来描述岩石在水射流冲击下的失效行为，当单元的最大主应力超过材料的抗拉强度或抗剪强度时单元失效破坏：

在水射流冲击损伤破岩模型中，采用花岗岩作为岩石材料，因为上述大部分参数都可以直接或间接获得，而且产地对花岗岩力学特性影响不大，花岗岩的JH-2模型参数如表2所示[22]。

表2 花岗岩的JH-2模型参数

1.3 水射流冲击损伤破岩几何模型

水射流冲击损伤破岩几何模型如图1所示，水射流简化为20 mm×2 mm的矩形水束，共640个SPH粒子。

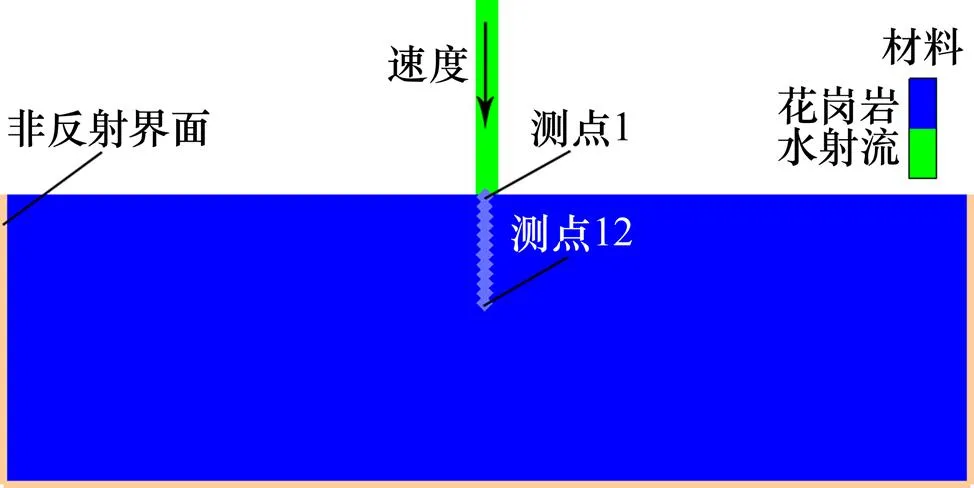
图1 几何模型

岩石模型的长与高分别为100 mm和30 mm，划分出48 000个有限单元。为消除边界对损伤场的影响，除岩石上表面外，其他都施加无反射边界，并在岩石内部定义数个测量点(gauges)以测量岩石内部的应力、损伤因子等。

2 水射流损伤破坏岩石过程演化

为研究花岗岩在射流冲击损伤破坏过程，利用上述建立的数值模型、状态方程以及强度模型等，进行动态模拟研究。图2所示为花岗岩在800 m/s的射流冲击作用下的损伤、破坏以及失效过程。在冲击时间=2.2 μs射流冲击岩石作用的最初阶段，射流撞击岩石表面形成动压力并以应力波的形式向岩石内部传播，该过程中伴随着岩石的损伤和失效。从图2可见：射流冲撞岩石初期存在2种破坏区域，即由剪应力导致的剪切破坏区以及最大拉应力引起的破坏区。在射流连续冲击作用下，射流作用点区域受到持续的压应力作用，使岩石局部弹性势能不断增加，进而使剪切失效区域周围萌发拉伸失效的裂纹。在=6.0~12.0 μs阶段，萌生的裂纹在拉伸应力作用下在纵向不断扩展形成放射性裂纹，但花岗岩内部的层状裂纹扩展缓慢，几乎不影响花岗岩的宏观损伤破裂失效，该失效情况与文献[12]中实验结果一致。图2(d)所示为冲击时间12.0 μs时岩石的损伤场。从图2(d)可见：岩石的损伤值大致上随距离射流入射点远近而变化，且距离入射点越远，岩石损伤度越小，这主要是应力波损伤能力随传播距离逐渐降低。图3所示为不同位置单元的损伤失效过程。由图3可见：岩石单元的损伤失效是在瞬间内完成的，且呈阶跃性。两单元失效时间间隔越来越大，说明射流冲击能量在岩石内部是急剧衰减的，且射流损伤破岩过程是微秒量级。

冲击时间/μs: (a) 2.2; (b) 6.0; (c) 12.0; (d) 12.0

图2 岩石损伤破坏过程

Fig. 2 Processes of rock damage and failure

图3 岩石单元损伤过程

3 高强度岩石损伤过程的影响因素分析

3.1 入射角对岩石损伤场的影响

入射角是指射流轴线与岩石表面所成的夹角(≤90°)。图4所示为射流冲击速度为800 m/s，入射角分别为80°，70°，60°，50°，40°以及30°时，在=10 μs的岩石损伤场，其中入射角为90°时岩石损伤场如图5(d)所示。从模拟结果可见：射流以不同的入射角冲击损伤破岩时，其产生的岩石损伤场有明显的差异，故射流入射角是影响水射流冲击损伤破岩的1个重要参数。射流的入射角越小，由剪切作用主导产生的压碎区越小，纵向裂纹和层向裂纹的扩展长度也相应减小。当射流入射角较小时(如30°和40°)，没有放射性裂纹产生，层状裂纹也未能得到有效的扩展，其主要是因为：当射流入射角较小时，受到岩石表面液动摩擦因数的影响，射流冲击能量未能有效地正向撞击损伤岩石，导致此时对岩石的损伤破坏效果较差。当射流的入射角较大时(如70°和80°等)，射流冲击损伤破岩效果较好，其主要是因为：射流近似于垂直冲击岩石时冲击能量得到有效的利用，应力波损伤破岩能力增强，岩石损伤区域增大。从以上分析可见：在射流冲击损伤破岩过程中，射流的入射角存在1个临界值，大于70°时冲击损伤破岩效果较好。模拟结果与文献[4]中实验结果变化规律类似，其中文献[4]存在1个最优值主要是实验中偏斜一定角度的射流容易将损伤破坏的岩石碎渣带走引起的，而射流垂直入射则阻碍此过程。

入射角/(°): (a) 80; (b) 70; (c) 60; (d) 50; (e) 40; (f) 30

图4 入射角对岩石损伤场的影响

Fig. 4 Rock damage field with different incidence angles

3.2 冲击速度对岩石损伤场的影响

射流冲击损伤破岩实际上是射流能量在岩石中传播和衰减过程。射流速度决定射流的冲击能量，其对岩石的损伤破坏场有直接的影响。图5所示为花岗岩分别在200，400，600以及800 m/s冲击速度下，=10 μs时的岩石损伤场。从数值模拟结果可见：射流冲击速度越大，其损伤破岩能力越强，损伤范围也越大。当射流速度为200 m/s时，射流对岩石的冲击损伤主要集中于射流入射点下方，且对岩石的损伤深度和范围都比较有限，在表面形成很小的破碎坑。当射流速度为400 m/s时，岩石损伤失效区域变大，且在失效区周围萌生、扩展了放射性裂纹，但此时岩石内无层状裂纹产生。当射流速度为600 m/s时，射流损伤能力进一步增强，岩石损伤范围变大，且在岩石内部萌生、扩展了层状裂纹。当射流速度为800 m/s时，放射性裂纹扩展更为显著，此时射流能量可以损伤至底部的岩石单元。从数值模拟结果可见：射流速度过小难以对岩石进行高效损伤破坏，主要以冲蚀作用破坏岩石的表面；射流速度达到一定值时才能够使岩石出现层状裂纹，产生体积破坏，如本文花岗岩的有效冲击损伤破坏速度应不小于600 m/s。

冲击速度/(m∙s−1): (a) 200; (b) 400; (c) 600; (d) 800

图5 岩石在不同冲击速度下的损伤场

Fig. 5 Rock damage field with different impact velocities

3.3 平移速度对对岩石损伤场的影响

在实际环境中，射流损伤破岩时通常具有一定的平移速度。图6所示为在射流冲击速度为600 m/s，平移速度分别为10，20，30和40m/s，=10 μs时的岩石损伤场。从图6可见：射流平移速度对岩石的纵向损伤深度影响不大，也对放射性裂纹的萌生、扩展影响很小，这主要由于射流平移速度相对于冲击速度而言很小，而射流损伤破岩过程在微秒量级。平移速度对层状裂纹的扩展形式有一定的影响，平移速度在对平移方向上的层状裂纹扩展有积极的作用，这主要是射流冲击岩石表面在平移方向上产生较大的张拉力引起的。总的来说，当射流平移速度比冲击速度小很多时，其对射流冲击岩石损伤场影响不大。

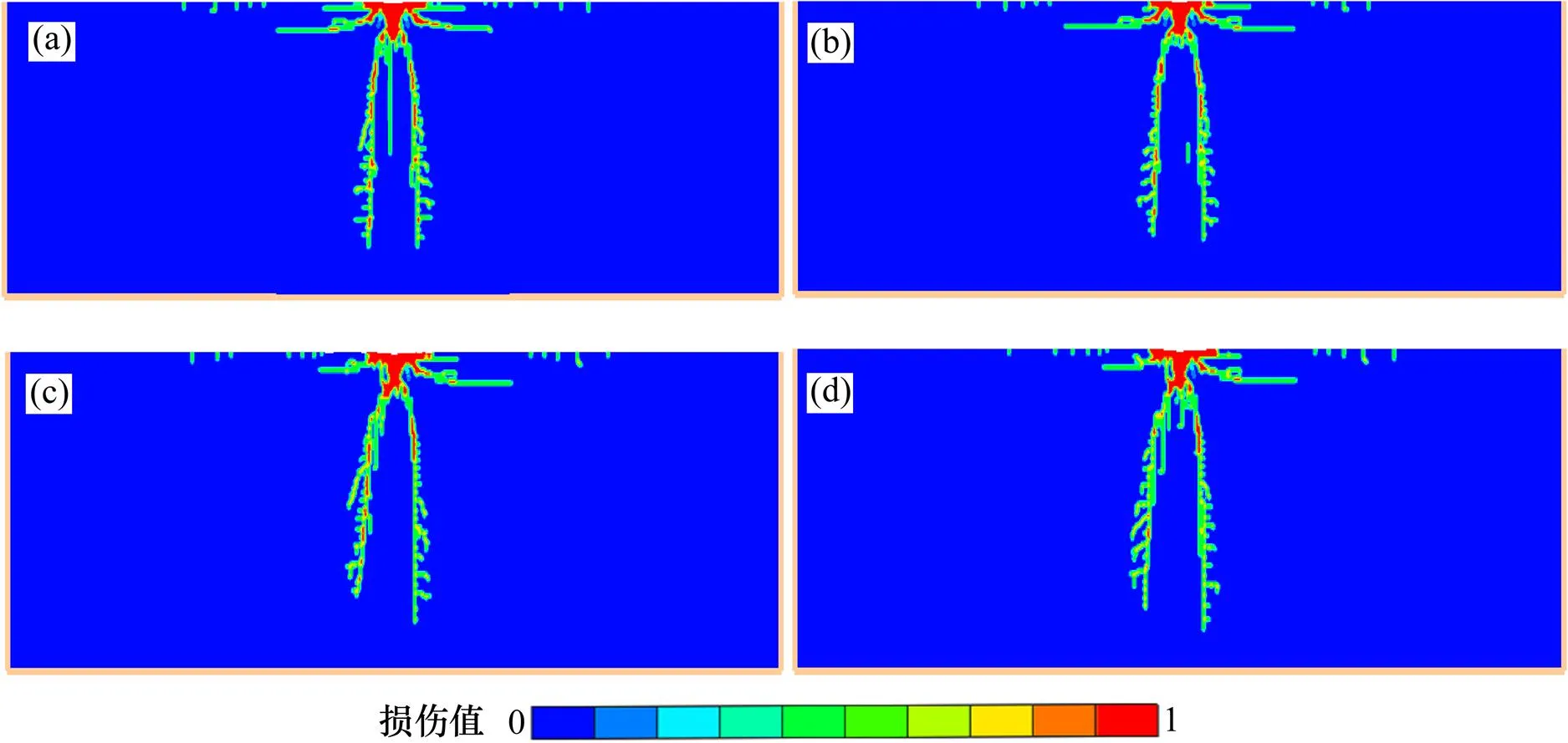
平移速度/(m∙s−1): (a) 10; (b) 20; (c) 30; (d) 40

图6 岩石在不同平移速度下的损伤场

Fig. 6 Rock damage field at different translation velocities

4 结论

1) 引入Johnson-Holmquist modelⅡ(JH-2)表征岩石力学特性，利用SPH/FEA耦合算法建立了高压水射流冲击破岩模型，很好地重现了水射流损伤破岩过程中岩石失效、裂纹扩展以及单元损伤破坏过程，对水射流冲击破岩机理的研究有一定的参考意义。

2) 高压水射流冲击损伤破坏岩石过程中存在2种失效破坏区域，即剪切破坏区和拉伸破坏区：剪切破坏区主要集中在射流入射点下方，形成岩石的冲击粉碎区；拉伸破坏主要出现在远离射流入射点区域，其主导放射性裂纹和层状裂纹的萌生、扩展。此外，岩石单元的损伤破坏呈阶跃性，损伤过程为微秒量级，且距射流入射点越近的岩石损伤程度越大。

3) 射流的入射角和冲击速度对岩石损伤场影响较大，而射流平移速度对岩石损伤场影响不大：射流冲击速度较小时以冲蚀破坏岩石为主，射流达到一定值才能够有效损伤破坏岩石，产生放射性裂纹和层状裂纹，本文射流的有效冲击速度为600 m/s；射流冲击损伤破坏岩石过程中，射流入射角存在一个最佳区域，大于70°时损伤破坏岩石效果较好；由于射流平移速度较冲击速度小得多，其对射流冲击岩石损伤场影响不明显。

[1] 廖华林, 李根生, 熊伟. 超高压水射流辅助破岩钻孔研究进展[J]. 岩石力学与工程学报, 2002, 21(2): 2583−2587.
LIAO Hualin, LI Gengsheng, XIONG Wei.[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(2): 2583−2587.

[2] 李根生, 廖华林. 超高压水射流冲蚀切割岩石断口微观断裂机理实验研究[J]. 高压物理学报, 2005, 19(4): 337−343.
LI Gensheng, LIAO Hualin. Micro-Failure mechanism analysis and test study for rock failure surface under water jet impact[J]. Chinese Journal of High Pressure Physics, 2005, 19(4): 337−343.

[3] Guo C W, Dong L. Energy consumption in communication of mica with cavitation abrasive water jet[J]. Journal of China University of Mining & Technology, 2007, 17(2): 251−254.

[4] 冯云春, 徐依吉, 赵付国. 超高压淹没射流破岩规律实验研究[J]. 高压物理学报, 2005, 19(1): 66−71.
FENG Yunchun, XU Yiji, ZHAO Fuguo. Experimental study on the breaking of rock by ultra-high pressure water jetting[J]. Chinese Journal of High Pressure Physics, 2005, 19(1): 66−71.

[5] 李根生, 廖华林, 黄中伟, 等. 超高压水射流作用下岩石损伤破碎机理[J]. 机械工程学报, 2009, 45(10): 285−293.
LI Gensheng, LIAO Hualin, HUANG Zhongwei, et al. Rock damage mechanisms under ultra high pressure water jet impact[J]. Journal of Mechanical Engineering, 2009, 45(10): 285−293.

[6] Momber A W. Deformation and fracture of rock due to high-speed liquid impingement[J]. International Journal of Fracture, 2004, 130: 683−704.

[7] 刘佳亮, 司鹄. 高压水射流破碎高围压岩石损伤场的数值模拟[J]. 重庆大学学报, 2011, 34(4): 40−46.
LIU Jialiang, SI Hao. Numerical simulation on damage field of high pressure water jet breaking rock under high ambient pressure[J]. Journal of Chongqing University, 2011, 34(4): 40−46.

[8] 廖华林, 李根生. 超高压水射流冲击岩石的流固耦合分析[J]. 水动力学研究与进展, 2004, 19(4): 453−457.
LIAO Hualin, LI Gensheng. Fluid-structure interaction of high pressure jets impinging on rock[J]. Journal of Hydrodynamics, 2004, 19(4): 453−457.

[9] Ni H J, Wang R H, Zhang Y Q. Numerical simulation study on rock breaking mechanism and process under high pressure water jet[J]. Applied Mathematics and Mechanics (English Edition), 2005, 26(12): 1445−1452.

[10] 孙清德, 汪志明, 于军泉, 等. 高压水射流破岩规律的数值模拟研究[J]. 岩土力学, 2005, 26(6): 978−982.
SUN Qingde, WANG Zhiming, YU Junquan, et al. A disquisition on breaking mechanism of high pressure jet impacting on rock[J]. Rock and Soil Mechanics, 2005, 26(6): 978−982.

[11] 司鹄, 王丹丹, 李晓红. 高压水射流破岩应力波效应的数值模拟[J]. 重庆大学学报, 2008, 31(8): 942−945.
SI Hao, WANG Dandan, Li Xiaohong. Stress wave effect in numerical simulation on rock breaking under high pressure water jet[J]. Journal of Chongqing University, 2008, 31(8): 942−945.

[12] 卢义玉, 张赛, 刘勇, 等. 脉冲水射流破岩过程中的应力波效应分析[J]. 重庆大学学报, 2012, 35(1): 117−124.
LU Yiyu Y, ZHANG Sai, LIU Yong, et al. Analysis on stress wave effect during the process of rock breaking by pulsed jet[J]. Journal of Chongqing University, 2012, 35(1): 117−124.

[13] Wang J M, Gao N, Gong W J. Abrasive water-jet machining simulation by coupling smoothed particle hydrodynamics/finite element method[J]. Chinese Journal of Mechanical Engineering, 2010, 23(1): 1−6.

[14] 马利. 无网格法及液体射流高速碰撞与侵彻模拟[D]. 杭州: 浙江大学航空航天学院, 2007: 61−62, 76.
MA Li. Mesh-free method and its application on high velocity fluid jet impact and penetration simulation[D]. Hangzhou: Zhejiang University. School of Aeronautics and Astronautics, 2007: 61−62, 76.

[15] Ma L, Bao R, Guo Y. Waterjet penetration simulation by hybrid code of SPH and FEA[J]. International Journal of Impact Engineering, 2008, 35(9): 1035−1042.

[16] Limido J, Espinosa C, Salaun M, et al.[J]. International Journal of Mechanical Sciences, 2007, 49: 898−908.

[17] 倪红坚, 王瑞和, 葛洪魁. 高压水射流破岩的数值模拟分析[J]. 岩石力学与工程学报, 2004, 23(4): 550− 554.
NI Hongjian, WANG Ruihe, GE Hongkui. Numerical simulation on rock breaking under high pressure waterjet[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(4): 550−554.

[18] Century Dynamics Inc. Autodyn theory manual[Z]. Concord, CA: Century Dynamics Inc, 2003: 177−178.

[19] Holmquist T J, Templeton D W, Bishnoi K D. Constitutive modeling of aluminum nitride for large strain, high strain rate, and high-pressure application[J]. International Journal of Impact Engineering, 2001, 25(3): 211−231.

[20] 朱哲明, 王超, 王蒙, 等. 爆炸载荷作用下缺陷岩体破坏特征的数值模拟研究[J]. 四川大学学报(工程科学版), 2011, 43(2): 1−8.
ZHU Zheming, WANG Chao, WANG Meng, et al. Numerical predication on the fracture characteristics of rock with defects under blasting loads[J]. Journal of Sichuan University (Engineering Science Edition), 2011, 43(2): 1−8.

[21] 朱哲明, 李元鑫, 周志荣, 等. 爆炸载荷下缺陷岩体的动态响应[J]. 岩石力学与工程学报, 2011, 30(6): 1157−1167.
ZHU Zheming, LI Yuanxin, ZHOU Zhirong, et al. Dynamic response of defected rock under blasting load[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(6): 1157−1167.

[22] Dehghan Banadaki M M, Mohanty B. Numerical simulation of stress wave induced fractures in rock[J]. International Journal of Impact Engineering, 2012, 40(2): 16−25.

Numerical analysis on damage field of rock fragmentation with water jet

JIANG Hongxiang, DU Changlong, LIU Songyong, GAO Kuidong

(School of Mechanical and Electrical Engineering, China University of Mining & Technology, Xuzhou 221116, China)

A constitutive model, Johnson-Holmquist modelⅡ(JH-2) for brittle material was adopted to characterize the mechanical properties of rock. And the numerical model of rock breaking with high-pressure water jet impacting was established with coupling Smoothed Particle Hydrodynamics (SPH) method and finite element analysis (FEA) method. It well simulated the rock failure, cracks propagation and the variations of rock element damage in different positions. Moreover, the effects of impact velocity, incidence angle and translation velocity of water jet on rock damage field were investigated. The results show that rock damage, failure and cracks propagation are caused by shear and tensile action combinations. The damage and failure zone of rock near the jet impacting point is mainly due to shear action; however, the radial and spall cracks propagation are dominated by tensile action. The damage of rock element represents a step changing with time, and the response of rock damage and failure process under water jet impacting is within microseconds. The incidence angle of water jet impacting rock has an effective range, and better damage effect can be obtained when the incidence angle is more than 70o. The surface erosion of rock is primary with low impact velocity of water jet, actual damage and failure of rock as radial and spall cracks occurrence can be achieved only when impact velocity of water jet reaches a certain value. The effect of water jet translation velocity on rock damage field is not remarkable because the translation velocity of water jet is much smaller than its impact velocity.

water jet; SPH; FEA; rock damage and failure; JH-2 constitutive model

TD825

A

1672−7207(2015)01−0287−08

2014−02−13；

2014−04−20

国家高科技研究发展计划(863计划)项目(2012AA062104)；国家自然科学基金面上资助项目(51375478)；江苏高校优势学科建设工程资助项目(SZBF2011-6-B35) (Project(2012AA062104) supported by the National High Technology Research and Development Program (863 Program); Project(51375478) supported by the National Natural Science Foundation of China; Project(SZBF2011-6-B35) supported by the Priority Academic Program Development of Jiangsu High Education Institute of China)

杜长龙，教授，博士生导师，从事高压水射流破岩技术研究；E-mail: jdjxx3@cumt.edu.cn

10.11817/j.issn.1672−7207.2015.01.039

(编辑 杨幼平)