单载波通信系统的迭代频域合成均衡算法

乔 良 辛吉荣② 郑 辉



单载波通信系统的迭代频域合成均衡算法

乔 良*①辛吉荣①②郑 辉①

①(盲信号处理重点实验室 成都 610041)②(国防科学技术大学电子科学与工程学院 长沙 410073)

为提高符号间干扰(ISI)信道条件下信号接收的可靠性，该文研究单载波通信系统的多天线空间分集接收问题，提出一种迭代频域合成均衡算法。该算法推导先验信息条件下合成均衡器的频域传输函数，并借助快速傅里叶变换(FFT)实现合成均衡器系数和均衡滤波的高效计算。仿真结果表明，相比时域算法，该算法能够在不损失性能的前提下，大幅降低运算复杂度。与单载波频域均衡(SC-FDE)算法相比，该算法不需要在数据传输的结构中插入循环前缀(CP)，提高频谱利用率，能够直接应用于现有单载波通信系统。

无线通信；空间分集；频域均衡；符号间干扰

1 引言

无线通信系统中，信道的多径和衰落效应导致接收信号中产生符号间干扰(InterSymbol Interference, ISI)。信道均衡是补偿信道畸变、消除ISI的有效手段，但是对于严重ISI信道，均衡处理的信号中仍然会出现较高的误码率。采用多个接收天线的空间分集技术能够减小接收机遭遇信道衰落的深度和衰落的持续时间，从而提高信号传输的可靠性。空间分集与信道均衡技术的结合能够在减小信道衰落影响的同时消除ISI，提高通信的可靠性。

Turbo均衡[1]是一种在均衡器和译码器之间迭代交换软信息的算法，它在信道均衡时充分利用了纠错编码的增益，因此在相同的信道条件下其性能优于传统均衡算法。近年来，Turbo均衡被广泛应用于短波[2]、水声通信[3]、OFDM[4]等领域。在迭代均衡与空间分集的联合优化方面，文献[5]提出了一种迭代合并均衡算法，根据最小均方误差(Minimum Mean Square Error, MMSE)准则，将多路接收信号以及译码器反馈的先验信息送入合成均衡器，同时完成分集合成和信道均衡。文献[6]在水声通信的背景下提出了一种空间分集自适应Turbo均衡算法，该算法在符号合成时使用了简单的等增益合成，无法达到最优的均衡合成性能。

文献[5]和文献[6]都是从时域均衡的角度开展研究，近年来单载波频域均衡(Single Carrier Frequency Domain Equalization, SC-FDE)的研究受到广泛关注，同时域均衡相比，频域均衡借助于快速傅里叶变换(FFT)实现，具有更低的计算复杂度。文献[7]在移动通信的环境下研究了一种低复杂度的MMSE Turbo均衡，该算法借助FFT实现了滤波器系数的高效计算，但是均衡滤波部分仍然在时域完成。文献[8]提出了一种迭代分组判决反馈均衡器(Iterative Block Decision Feedback Equalizer, IBDFE)，按照MMSE准则推导了前向均衡器和反馈均衡器系数的迭代计算方法。文献[12]在具有大多径时延和多普勒频移的水声信道背景下研究了IBDFE算法，提出了一种联合迭代均衡和频域信道估计算法，其研究指出，IBDFE的性能优于传统时域DFE，并且具有更低的计算复杂度。文献[13]针对高阶连续相位调制(Continuous Phase Modulation, CPM)信号，从Rimoldi分解的角度出发，通过设计CPM信号发射帧结构，提出了一种适应于高阶CPM信号的Turbo频域均衡算法。但是，上述SC-FDE算法需要在数据传输的结构中插入循环前缀(Cyclic Prefix, CP)，用于将信道的线性卷积关系转换为循环卷积。显然，CP的引入一方面降低了频谱的利用效率，另一方面使得FDE无法直接应用于现有单载波通信系统。

本文研究了单载波通信系统的多天线分集接收问题，从频域的角度将Turbo迭代均衡与分集接收相结合，提出了一种迭代频域合成均衡算法。该算法不需要在数据传输中插入CP，同时能够有效降低计算复杂度，能够直接应用于现有单载波通信系统。计算机仿真的结果表明，本文算法通过在合成均衡器与信道译码器之间迭代交换外信息，充分利用了多天线接收和信道译码的增益，其性能接近于理想无符号间干扰信道分集合成的性能。

2 信号模型

图1 离散时间等效信道模型

3 软输入软输出(SISO)频域合成均衡器

本节在先验信息条件下，推导了合成均衡器前向部分和反馈部分的频域传输函数。频域合成均衡器的结构如图2所示，其中是个前向滤波器的频率响应，对应的时域系数为,是反馈滤波器的频率响应，对应的时域系数为,是软符号估计值，反映了上次迭代反馈的先验信息。

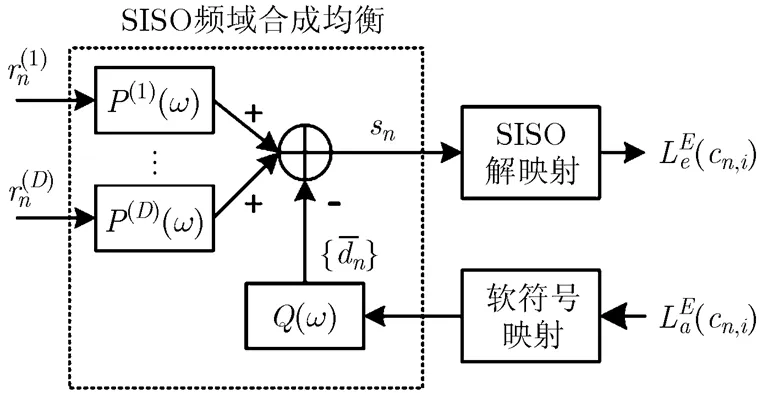
图2 SISO频域合成均衡的结构图

3.1输出信噪比的时域表示

这时合成均衡器输出信噪比的表达式为

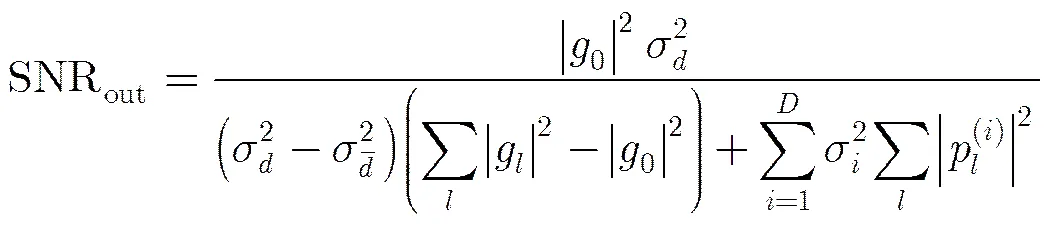
3.2输出信噪比的频域表示

根据Parseval定理，

另外，

3.3最大输出信噪比准则确定合成均衡器的频域传输函数

根据Cauchy-Schwarz不等式，输出信噪比的上界为

因此

另外，根据式(17)，有

联立式(18)和式(19)，可以推出

此时合成均衡器的输出信噪比可以表示为

4 迭代频域合成均衡

接收机中迭代频域合成均衡的整体结构如图3所示，软输入软输出(Soft Input Soft Output, SISO)频域合成均衡器输出的均衡符号记为, SISO解映射模块将均衡符号转化为对应编码比特的外信息，经过解交织后作为译码器的先验信息用于SISO译码。译码器在输出信息序列硬判决的同时更新编码比特的外信息，经过交织后作为频域合成均衡器的先验信息，软符号映射模块将比特外信息转化为对应的软符号值，用于下次迭代处理。首次迭代时比特的外信息为零，相应的软符号值。

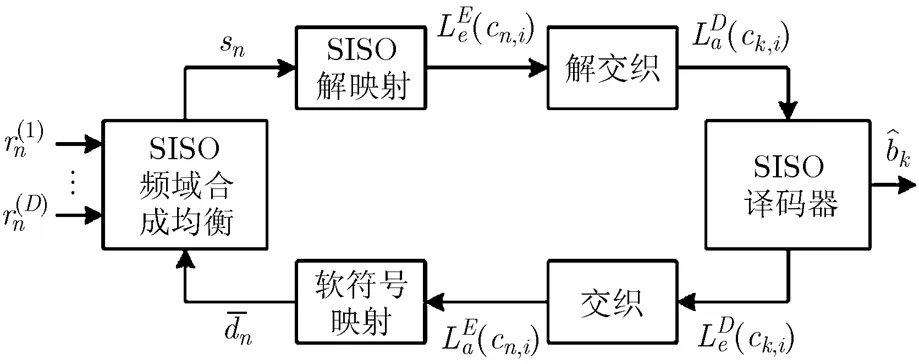
图3 迭代频域合成均衡的处理结构

4.1 SISO解映射

4.2 软符号映射

5 频域合成均衡器的具体实现

5.1频域合成均衡器的计算步骤

第3节给出了合成均衡器前向部分和反馈部分应该满足的频域形式，如果用横向滤波器精确实现该结构，则需要无限长滤波器，在实际实现中一般计算个离散频点的频域响应来近似该结构，从时域来看，也可以理解为对应均衡滤波器的长度。SISO频域合成均衡器的具体计算步骤为：

5.2 计算复杂度分析

表1比较了本文算法同文献[5]中时域迭代合并均衡算法(Minimum Mean Square Error Iterative Combining Equalization, MMSE-ICE)、文献[14]中频域判决反馈迭代频域均衡算法(Frequency Domain Equalization with Frequency Domain Decision Feedback, FDE-FDDF)的计算复杂度，运算量分为均衡器系数计算和均衡滤波两部分，单位为复数乘法次数。统计中假设本文算法的均衡器系数每点更新一次，维矩阵求逆的运算量为,点FFT的运算量为。括号内的数字表示当取典型值,,,时，具体的运算量数值。从表1可以看出，相比时域MMSE-ICE算法，本文算法有效降低了计算复杂度；而同单天线接收的FDE-FDDF算法相比，因为本文算法利用了多个接收天线，问题规模更大，因此运算量要大于FDE-FDDF。表中典型条件下，本文算法的运算量约为FDE-FDDF的2.7倍，这在实际应用中是可以接受的。

表1不同算法每个接收符号每次迭代所需的运算量

算法均衡器系数计算均衡滤波 时域MMSE-ICE(多天线)(65442)(128) FDE-FDDF(单天线)(13)(12.5) 本文算法(多天线)(26)(43.5)

6 计算机仿真

信号调制方式为QPSK，信道编码方式为1/2码率非系统卷积编码，其生成多项式，每帧信息比特的长度为1024 bit，最后6 bit为结尾比特，用于编码器结束于零状态，交织器为2048 bit的S伪随机交织器，迭代次数取为4次，信道译码使用max-log-MAP算法，仿真中假设各分集支路的接收信噪比相同，信道冲激响应精确已知，数据交叠长度。

图4 FFT点数对迭代频域合成均衡算法的性能影响

6.2静态信道条件下，迭代频域合成均衡的误码性能

仍然考虑6.1小节中的静态ISI信道条件，图5给出了本文算法在两天线和单天线接收时的误码性能，同时给出了文献[14]中频域判决反馈迭代频域均衡算法(FDE-FDDF)的性能曲线。需要指出的是，FDE-FDDF算法仅考虑了单天线接收条件，因此只能与本文算法退化到单天线时的性能进行比较。从图5可以看出，本文算法在单天线条件下的性能与FDE-FDDF算法非常接近，甚至在严重ISI信道下还略优于FDE-FDDF。而将两天线接收的性能同单天线进行比较可以发现，达到误码率，信道1需要的约为10 dB，信道2需要的约为5 dB，而两分集迭代频域合成均衡只需要约0.5 dB，非常接近于两个理想无符号间干扰信道分集合成的性能，同时4次迭代所带来的性能增益约为3 dB(3.5 dB0.5 dB)，因此本文迭代频域合成均衡算法有效改善了接收系统的处理增益，降低了信号接收的信噪比需求。

图5 静态信道条件下，两分集迭代频域合成均衡的误码性能

6.3块衰落信道条件下，迭代频域合成均衡的误码性能

仿真采用6径瑞利衰落信道，多径之间的时延间隔为符号周期，6条多径具有相等的平均功率。仿真中信道假设为块衰落(block fading)的，即在一帧之内信道是固定的，不同帧之间的信道独立随机产生，10000次Monte Carlo仿真结果统计。

图6给出了块衰落信道条件下，当接收天线数目分别为1, 2, 4时，本文迭代频域合成均衡算法的性能，同时在单天线条件下给出了文献[14]中FDE- FDDF算法的性能作为对比。与6.2小节的仿真结果类似，本文算法在单天线条件下的性能与FDE- FDDF算法非常接近。从图中可以看出，接收天线数目的增加能够有效提高接收系统的误码性能，1天线接收条件下，达到误码率需要的约为5.4 dB，当2天线接收时，需要的约为0.4 dB，而当4天线接收时，仅需要-2.6 dB。同理想无符号间干扰信道分集接收的性能相比，当接收天线数为1时，即使采用迭代均衡算法，其性能距离性能界仍然约有2 dB的性能差距，而当接收天线数为2和4时，迭代频域合成均衡的性能已经能够达到性能界。另一方面，由于分集合成改善了信道中的ISI，随着接收天线数目的增加，迭代处理的增益逐渐减小，1天线接收时，迭代增益约为2.9 dB(8.3 dB5.4 dB), 2天线接收时，迭代增益约为1.8 dB(2.2 dB0.4 dB), 4天线接收时，迭代增益只有约0.7 dB (-2.6 dB-1.9 dB)。

图6 块衰落信道，不同分集接收支路数目，迭代频域合成均衡的误码性能

7 结束语

本文针对单载波通信系统的多天线迭代接收问题，提出了一种迭代频域合成均衡算法，该算法通过在合成均衡器和信道译码器之间迭代交换外信息，有效改善了接收机抗严重符号间干扰的能力。相比时域迭代均衡，本文算法有效降低了计算复杂度；相比频域均衡，本文算法避免了在数据帧中插入CP，提高了频谱利用效率，能够直接应用于现有单载波通信系统。这为宽带无线通信系统中消除符号间干扰，提高系统性能提供了一种新的接收处理方案。

参考文献

[1] Douillard C, Jezequel M, and Berrou C. Iterative correction of intersymbol interference: Turbo equalization[J]., 1995, 6(5): 507-511.

[2] Otnes R and Tüchler M. Improved receivers for digital high frequency waveforms using Turbo equalization[C]. Proceedings of IEEE Military Communications Conference, California, USA, 2002, 1: 99-104.

[3] Rafati A, Lou Huang, and Xiao Cheng-shan. Soft-decision feedback Turbo equalization for LDPC-coded MIMO underwater acoustic communications[J]., 2013, 39(1): 90-99.

[4] Wang Zhao-hui, Huang Jie, Zhou Sheng-li,.. Iterative receiver processing for OFDM modulated physical-layer network coding in underwater acoustic channels[J]., 2013, 61(2): 541-553.

[5] 高梅, 黄国策, 杜栓义, 等. 用于短波高速数据传输的迭代合并均衡算法[J]. 系统工程与电子技术, 2013, 35(9): 1954-1960.

Gao Mei, Huang Guo-ce, Du Shuan-yi,.. Iterative combining equalization algorithm for high data rate HF transmission[J]., 2013, 35(9): 1954-1960.

[6] Christophe L and Raphaël L B. Adaptive MMSE Turbo equalization with high-order modulations and spatial diversity applied to underwater acoustic communications[C]. Proceedings of 11th European Wireless Conference on Sustainable Wireless Technologies, Vienna, Austria, 2011: 1-6.

[7] Christophe L, Raphaël L B, and Dominique L. Low- complexity MMSE Turbo equalization: a possible solution for EDGE[J]., 2005, 4(3): 965-974.

[8] Benvenuto N and Tomasin S. Iterative design and detection of a DFE in the frequency domain[J]., 2005, 53(11): 1867-1875.

[9] Zhang Chao, Wang Zhao-cheng, Pan Chang-yong,.. Low complexity iterative frequency domain decision feedback equalization[J]., 2011, 60(3): 1295-1301.

[10] Luzio M, Dinis R, and Montezuma P. SC-FDE for offset modulations: an efficient transmission technique for broadband wireless systems[J]., 2012, 60(7): 1851-1861.

[11] Zhang Xiao-hui, Chen E, and Mu Xiao-min. Single-carrier frequency-domain equalization based on frequency-domain oversampling[J]., 2012, 16(1): 24-26.

[12] 张歆, 张小蓟. 水声信道中的迭代分组判决反馈均衡器[J]. 电子与信息学报, 2013, 35(3): 683-688.

Zhang Xin and Zhang Xiao-ji. Iterative block decision feedback equalization for underwater acoustic channels[J].&, 2013, 35(3): 683-688.

[13] 钟凯, 彭华, 葛临东. 基于Rimoldi分解的连续相位调制信号Turbo频域均衡算法[J]. 电子与信息学报, 2014, 36(5): 1190-1195.

Zhong Kai, Peng Hua, and Ge Lin-dong. Turbo frequency domain equalization algorithm based on Rimoldi decomposition for continuous phase modulation signals[J].&, 2014, 36(5): 1190-1195.

[14] Benjamin Ng, Chan-Tong L, and Facloner D. Turbo frequency domain equalization for single carrier broadband wireless systems[J]., 2007, 6(2): 759-767.

[15] Tüchler M and Singer A C. Turbo equalization: an overview[J]., 2011, 57(2): 920-952.

[16] Moulines E, Duhamel P, Cardoso J F,.. Subspace methods for the blind identification of multichannel FIR filters[J]., 1995, 43(2): 516-525.

Iterative Frequency Domain Combining Equalization Algorithm for Single Carrier Systems

Qiao Liang①Xin Ji-rong①②Zheng Hui①

①(,610041,)②(,,410073,)

To combat the effect of InterSymbol Interference (ISI) while transmitting data over wireless fading channels, the issue of single carrier communication signal receiving with multiple antennas is studied and an iterative frequency domain combining equalization algorithm is proposed. The proposed algorithm derives the theoretical frequency domain transfer function of the combining equalizer withinformation. An efficient implementation is proposed which employs the Fast Fourier Transform (FFT) to compute the combining equalizer coefficients and equalization filter. Numerical results show that the proposed algorithm reduces complexity enormously with nearly no performance loss compared with the time domain algorithm. Compared with Single Carrier Frequency Domain Equalization (SC-FDE), the Cyclic Prefix (CP) overhead can be avoided, and the computationally efficient frequency domain algorithm can be applied to the existing single carrier communication systems.

Wireless communication; Spatial diversity; Frequency domain equalization; InterSymbol Interference (ISI)

TN92

A

1009-5896(2015)08-1950-07

10.11999/JEIT141507

乔良 lqiao57s@163.com

2014-11-27收到，2015-04-28改回，2015-06-08网络优先出版

国家自然科学基金(61172140)资助课题

乔 良： 男，1984年生，博士生，工程师，研究方向为通信信号处理.

辛吉荣： 男，1985年生，博士生，工程师，研究方向为阵列信号处理.

郑 辉： 男，1957年生，博士生导师，高级工程师，研究方向为盲信号处理、智能信息处理.