基于互相关协方差矩阵的改进多重信号分类高分辨波达方位估计方法

毛琳琳 张群飞 黄建国 史文涛 韩 晶



基于互相关协方差矩阵的改进多重信号分类高分辨波达方位估计方法

毛琳琳*张群飞 黄建国 史文涛 韩 晶

(西北工业大学航海学院 西安 710072)

针对经典高分辨波达方位(DOA)估计方法在低信噪比下分辨性能较差的问题，该文提出一种适用于主动探测系统的基于互相关矩阵的改进多重信号分类(MUSIC)高分辨方位估计方法(I-MUSIC)。该方法首先利用主动声呐发射信号已知的特性，将发射信号与阵元接收信号进行互相关，利用互相关序列形成新的空域协方差矩阵，再进行特征分解。理论分析表明，互相关处理在抑制噪声的同时保留了阵元之间的相位信息，可以得到比MUSIC方法更准确的子空间划分，进而提高低信噪比方位估计性能。在此基础上，提出一种基于相关时间门限的改进MUSIC高分辨方位估计(T-MUSIC)方法，通过对互相关序列设置时间门限进一步提高方位估计信噪比。仿真结果表明，与MUSIC方法相比，I-MUSIC与T-MUSIC可以分别使低信噪比时的估计性能提高3 dB和6 dB，相应平均估计误差分别为原方法的77%和53%。在阵元间接收噪声存在相关性时，T-MUSIC与I-MUSIC方法相比可获得8 dB的估计增益，估计性能更优。I-MUSIC与T-MUSIC应用于多目标主动探测，可大幅提高探测系统在低信噪比下的方位估计性能。

信号处理；波达方位估计；互相关；协方差矩阵；多重信号分类

1 引言

高分辨波达方位(DOA)估计是阵列信号处理领域的重要研究内容之一，其应用涉及雷达、通信、声呐等诸多领域[1,2]。自20世纪80年代以来，出现了两大类经典高分辨方位估计方法。一类子空间拟合类方法，如最大似然(Maximum Likelihood, ML)法，加权子空间拟合法(Weighted Subspace Fitting, WSF)[6]等，构造阵列流型矩阵与阵列接收数据的子空间之间的拟合关系，通过最大或最小化拟合关系求解问题，得到未知参数的估计。但这些拟合类方法，由于寻求其全局最优解不可避免的多维非线性特性和计算复杂度，不易求解，实时性能差。针对子空间拟合类方法所存在的这些缺陷，近年来涌现了一批子空间拟合类快速算法，这类方法的本质是通过迭代过程求解拟合关系的最优解，如文献[7~9]等。这些方法提高了运算速度，但过程不直观，且迭代收敛与否又受到初始参数选取、优化设置等诸多因素限制，难于应用到复杂多变的水下探测环境中。还有一类是子空间分解类方法。这类方法利用阵列接收数据协方差矩阵的特征分解技术，并建立在信号子空间和噪声子空间正交性原理之上，如多重信号分类(MUltiple SIgnal Classification,MUSIC)[10,11]方法和最小模(Minimum Norm, MN)[12]方法。这类方法物理意义明确，是高分辨的次最优方法，在大样本或高信噪比的条件下能够获得精确的DOA值。目前对MUSIC方法的改进思路主要有两种，一种是改进空间谱峰的搜索机制以期获得更好的估计精度，如文献[13]，其改进建立在MUSIC方法本身对多目标有一定分辨能力的基础上；一种是以牺牲计算精度为代价，通过投影变换或在波束形成框架下简化问题来降低MUSIC方法计算复杂度，如文献[14~16]。二者均未考虑在低信噪比情况下，由于不能明显区分采样协方差矩阵的大特征值与小特征值，从而得到错误的子空间划分，导致MUSIC谱估计结果失效的问题。

为此，本文针对MUSIC方法提出了基于互相关矩阵的改进MUSIC高分辨方位估计方法(Improved MUSIC, I-MUSIC)。互相关法由于物理意义明确、计算量小，易于实现，被广泛地用于时延估计中。本文提出的I-MUSIC方法，利用互相关序列保留阵元间相位信息并抑制噪声的特性，基于发射信号与阵元接收信号的互相关序列形成空域协方差矩阵，再进行特征分解，可以得到比MUSIC方法更准确的子空间划分。在此基础上，为进一步提高方位估计信噪比，受到语音信号处理中根据能量门限进行端点检测的启发[20,21]，结合线性调频信号的时延分辨力，提出了一种基于相关时间门限的改进MUSIC高分辨方位估计(Time threshold MUSIC, T-MUSIC)方法。仿真结果表明，在低信噪比下，I-MUSIC与T-MUSIC的多目标方位估计分辨概率和估计精度均高于MUSIC。T-MUSIC通过设置时间门限淘汰部分纯噪声点，在阵元间接收噪声存在相关性时也表现出显著优势。

2 阵列信号模型

式中导向矢量

3 改进MUSIC方位估计方法

针对MUSIC方法在低信噪比下由于子空间划分错误而导致的估计失效问题，本文提出基于互相关矩阵的改进MUSIC高分辨方位估计(I-MUSIC)方法。

3.1互相关的协方差矩阵

考虑式(1)所示阵列接收数学模型，则根据互相关定义，可得发射信号与第个阵元接收数据之间的互相关函数为

为了便于推导，将式(4)所示互相关函数表示为如式(5)的矩阵形式：

阵列接收信号与发射信号的互相关矩阵为

Goldberg [1]认为某一语言型式，如果其形式或功能不能严格地从其组成成分或已知的结构中得到预测，就可以称为是一个“构式”，构式是“形式和意义的配对”。

则互相关矩阵的协方差矩阵为

根据式(10)，式(7)可以简写为

令

则互相关的协方差矩阵可表示为

综合式(12)，式(13)，可得

3.2互相关的协方差矩阵特征分解

首先给出推导过程中用到的特征值与特征向量的性质：如果线性变换在的一组基下的矩阵为，则可知在该组基下的矩阵为。称为的多项式。如果是的特征值，是属于的特征向量，则的特征值是，属于的特征向量仍为。

3.3基于互相关矩阵的I-MUSIC方位估计

即为I-MUSIC方法的谱估计表达式。根据式(19)在信号的参数范围内进行谱峰搜索，找出个最大值点对应的角度就是信号入射方位。

3.4基于互相关时间门限的T-MUSIC方位估计

实时处理中，接收数据矩阵长度有限，信号与噪声不能完全正交，噪声与信号的互相关矩阵不为零。随着阵元接收信噪比的降低，阵列接收的互相关信号在相关峰外包含信号功率小、噪声比重大，利用I-MUSIC方法进行方位估计的性能也随之变差。受到语音信号处理中根据能量门限进行端点检测的启发[21,22]，考虑通过给互相关函数设定时间门限，进一步抑制噪声，提高方位估计信噪比。

时间门限的设定原则是：充分利用相关峰值附近包含目标回波的信息，淘汰相关峰值以外只包含噪声的信息。时间门限设定需充分考虑探测系统的时延分辨力。模糊度函数限定了最佳信息处理条件下探测系统的时延和速度分辨能力。由模糊度函数性质可知，线性调频信号的时延分辨率为0.88/[22]，其中为带宽。当足够大时，线性调频信号的互相关函数满足：

(1)不同的相关峰值属于不同的目标回波时延；

(2)处于同一相关峰值相关半径内任意两点对应同一目标回波。

将式(20)代入式(6)，式(7)，即得基于互相关时间门限的协方差矩阵,进行特征分解得到估计的噪声子空间。根据与信号子空间中的方向矢量的正交性，构造式

即为T-MUSIC方法的谱估计表达式。

4 仿真与性能分析

本节针对舰船垂直尺度高分辨方位估计这一应用背景，建立一个3亮点仿真模型，利用计算机仿真从空间谱、分辨概率以及估计精度3个方面对MUSIC, I-MUSIC及T-MUSIC 3种方法的 DOA估计性能进行分析比较。仿真模型如图1所示，模型参数如表1所示。

图1 潜艇目标三亮点分布示意图

表1舰船仿真模型参数

阵元接收信噪比SNR=5 dB，采用阵元间距= 0.03 m的均匀线列阵接收回波信号，水平方向阵元数目为6，垂直方向阵元数目为4，发射信号为载频0=30 kHz，带宽=10 kHz的线性调频(Linear Frequency Modulation, LFM)信号。采样频率= 120 kHz，噪声为高斯白噪声，水下声传播速度= 1490 m/s。目标的真实距离和方位数据如表2所示。

表2目标距离及方位数据

图2(a)和图2(b)分别比较了SNR=5 dB 时MUSIC, I-MUSIC两种方法处理水平亮点与垂直亮点的空间谱。由图2(a)可以看出，对于3个水平亮点，MUSIC方法的第1、第2谱峰之间由于噪声功率叠加而升高，两峰之间谷很浅，估计性能较差；而I-MUSIC算法，由于采用了互相关抑制噪声，谱峰尖锐，旁瓣更低。图2(b)中I-MUSIC的估计性能也明显好于MUSIC方法。

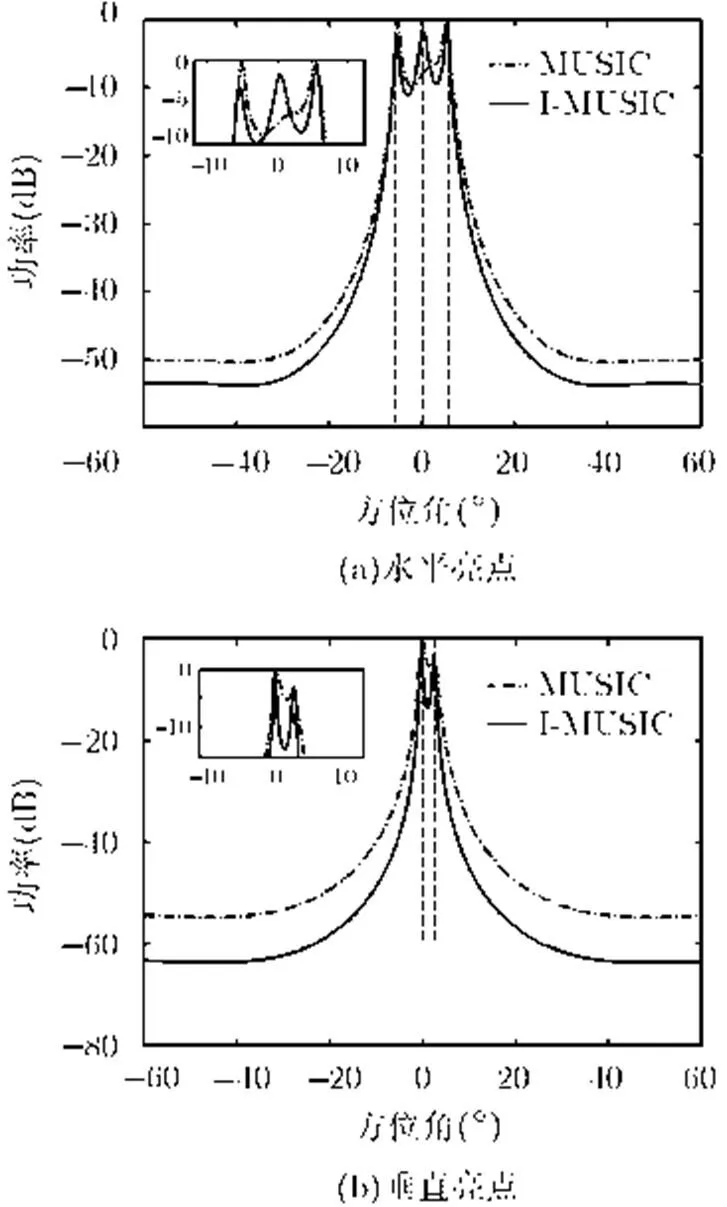
图2 空间谱图(SNR=5 dB)

图3(a)和图3(b)分别比较了SNR=0 dB 时MUSIC, I-MUSIC, T-MUSIC 3种方法处理水平亮点与垂直亮点的空间谱。可以看出，随着信噪比进一步降低，噪声功率增加，I-MUSIC对水平亮点与垂直亮点的估计性能均变差， T-MUSIC各谱峰间波谷较深，性能优势显著。

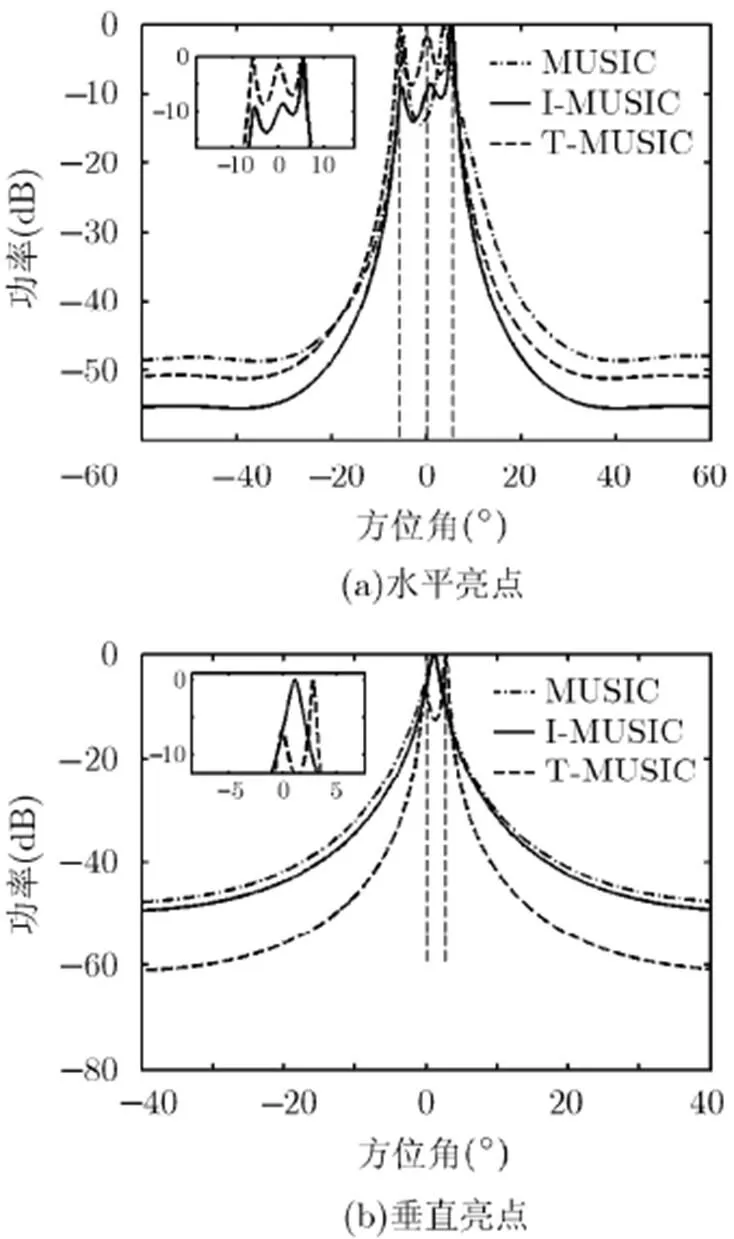
图3 空间谱图(SNR=0 dB)

图4和图5分别从分辨概率和估计精度(均方根误差RMSE) 两个方面来衡量比较了MUSIC, I-MUSIC, T-MUSIC 3种方法的估计性能。仿真实验中分辨概率是在若干次蒙特卡洛实验中，能够正确分辨两个或者多个目标的概率。对于相邻两个目标和，正确分辨需满足

RMSE 的计算是在可分辨的基础上进行的，其计算公式为

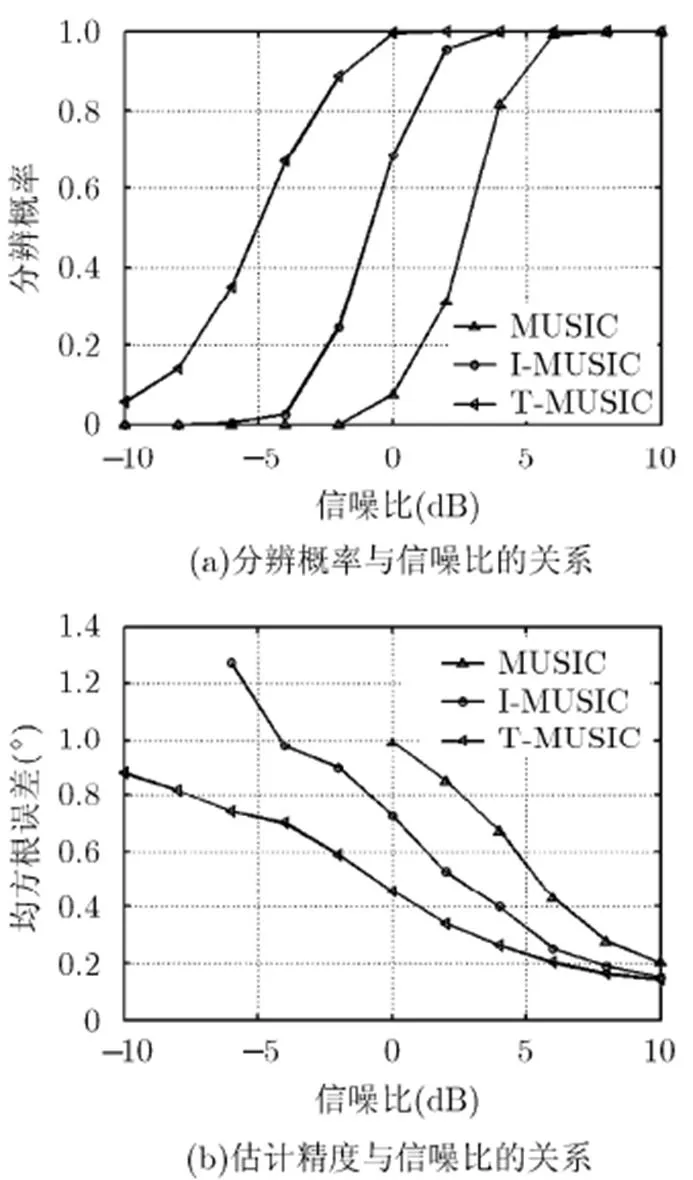
图4 水平亮点估计性能比较

观察图4 和图5可以看出，I-MUSIC方法低信噪比时对3个水平目标和两个垂直目标的估计性能，较MUSIC方法分别提升了4 dB和2 dB，对应0 dB时的估计误差分别为原方法的73.7%和81.3%。相应地，T-MUSIC方法的低信噪比估计性能，较MUSIC方法分别提高了8 dB和4 dB，相应0 dB时的估计误差分别为原方法的46.2%和60.8%。3种方法六元阵的性能均好于各自四元阵的情况。六元阵时，T-MUSIC与I-MUSIC方法对原MUSIC方法估计性能的提升幅度大于四元阵，因为当信噪比足够高时，阵元数代替信噪比成为制约方位估计性能的主要因素。

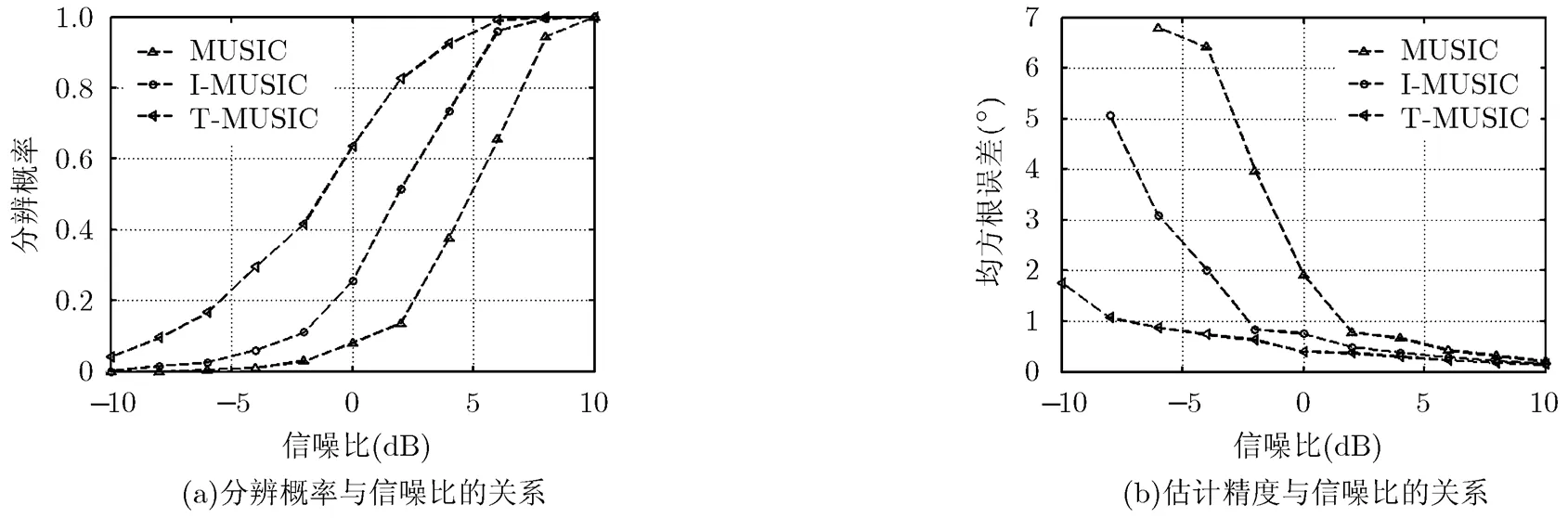
图5 垂直亮点估计性能比较

图6给出了阵元间接收噪声相关系数为0.5时，MUSIC, I-MUSIC, T-MUSIC 3种方法处理水平亮点的估计性能。为避免相关噪声方位信息对0°方向目标增强造成估计性能更好的假象，考虑3个亮点的水平方位角分别为,和的情况，其余参数同表2。

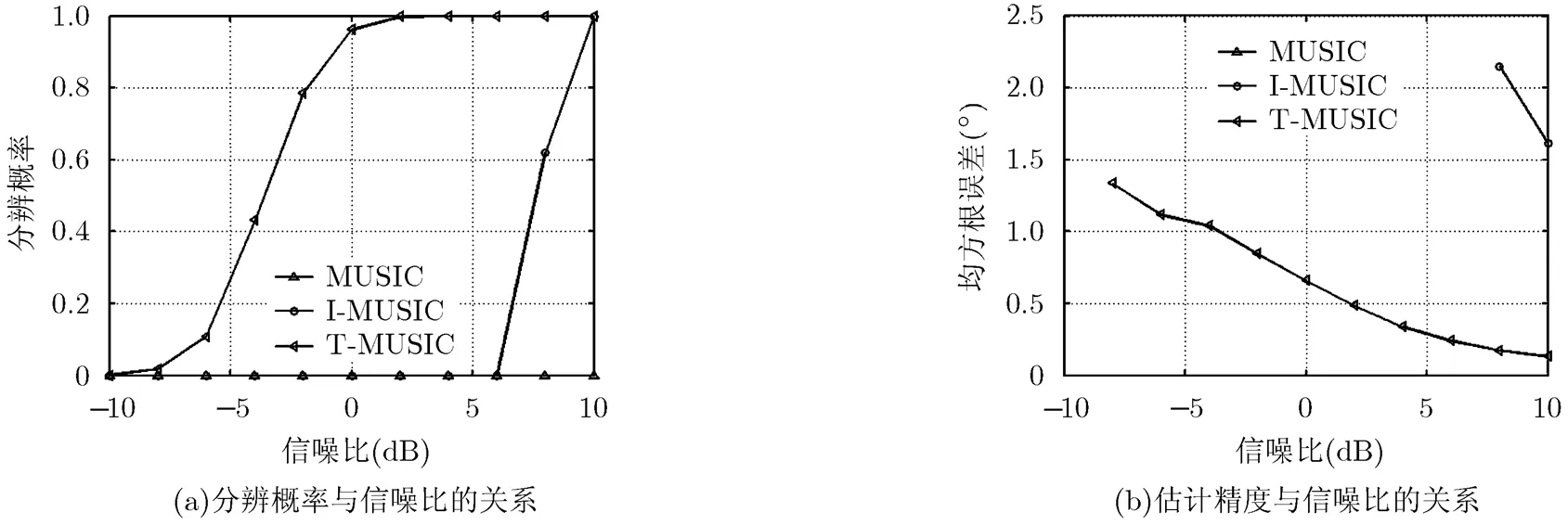
图6 阵元间接收噪声相关时水平亮点估计性能比较

对比图4与图6可以看出，在阵元间接收噪声相关时，MUSIC方法完全无法分辨3个水平亮点，总体估计性能严重恶化；I-MUSIC的分辨概率与估计精度大幅度下降；而T-MUSIC由于淘汰了纯噪声点，受噪声干扰较小，分辨概率和估计精度仅有小幅度下降，与I-MUSIC相比可以获得8 dB的估计增益，性能优势显著。

5 结束语

针对MUSIC方位估计方法在低信噪比下分辨性能较差的问题，利用互相关序列保留阵元间相位信息并抑制噪声的特性，提出了一种基于互相关矩阵的改进MUSIC高分辨方位估计(I-MUSIC)方法，给出了利用互相关矩阵的协方差矩阵代替阵列接收数据协方差矩阵进行特征分解进行方位估计的完整理论推导过程，进而提出了一种基于相关时间门限的改进MUSIC高分辨方位估计(T-MUSIC)方法，给出了时间门限选取方法，并进行了仿真性能研究。仿真结果表明，I-MUSIC和T-MUSIC方法应用于多目标主动探测，可以分别获得3 dB和6 dB的平均估计增益，相应平均估计误差分别为原方法的77%和53%，大幅提高了低信噪比下的多目标方位估计性能。T-MUSIC在阵元间接收噪声存在相关性时也表现出显著优势，为低信噪比下的主动探测提供了新思路。

参考文献

[1] Cheng Q, Lei H, and So H C. Improved unitary root-MUSIC for DOA estimation based on pseudo-noise resampling[J]., 2014, 21(2): 140-144.

[2] Zeng W, So C and Lei H.l-MUSIC: Robust direction-of- arrival estimator for impulsive noise environments[J]., 2013, 61(17): 4296-4308.

[3] Vincent F, Besson O, and Chaumette E. Approximate maximum likelihood direction of arrival estimation for two closely spaced sources[C]. Proceedings of the 2013 IEEE 5th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), St. Martin, France, 2013: 320-323.

[4] Heidenreich P and Zoubir M. Fast maximum likelihood DOA estimation in the two-target case with applications to automotive radar[J]., 2013, 93(12): 3400-3409.

[5] Lee Y, Hudson E, and Yao K. Acoustic DOA estimation: an approximate maximum likelihood approach[J]., 2014, 8(1): 131-141.

[6] Park S, Choi H, Yang W,Direction of arrival estimation using weighted subspace fitting with unknown number of signal sources[C]. Proceedings of the 11th International Conference on Advanced Communication Technology, Piscataway, USA, 2009: 2295-2298.

[7] Wang H, Kay S, and Saha S. An importance sampling maximum likelihood direction of arrival estimator[J]., 2008, 56(10): 5082-5092.

[8] Li X and Huang J. Bayesian high resolution DOA estimator based on importance sampling[C]. Proceedings of IEEE Oceans 2005, Washington, D.C., USA, 2005, 1: 611-615.

[9] Shi W, Huang J, and Hou Y. Fast DOA estimation algorithm for MIMO sonar based on ant colony optimization[J]., 2012, 23(2): 173-178.

[10] Yan F G, Jin M, and Qiao X L. Source localization based on symmetrical MUSIC and its statistical performance analysis[J]., 2013, 56(6): 1-13.

[11] Di C, Elio D, and Giovanni J. Wideband source localization by space-time MUSIC subspace estimation[C]. Proceedings of 2013 8th International Symposium on Image and Signal Processing and Analysis (ISPA), Trieste,Italy, 2013:331-336.

[12] Choi W and Sarkar K. Minimum norm property for the sum of the adaptive weights for a direct data domain least squares algorithm[J]., 2006, 54(3): 1045-1050.

[13] Rangarao V and Venkatanarasimhan S. Gold-MUSIC: a variation on music to accurately determine peaks of the spectrum[J]., 2013, 61(4): 2263-2268.

[14] Yan F, Jin M, and Qiao X. Low-complexity DOA estimation based on compressed MUSIC and its performance analysis[J]., 2013, 61(8): 1915-1930.

[15] Reddy V, Ng B, and Khong A. Insights into MUSIC-like algorithm[J]., 2013, 61(10): 2551-2556.

[16] Ying Z and Boon P. MUSIC-like DOA estimation without estimating the number of sources[J]., 2010, 58(3): 1668-1676.

[17] Azaria M and Hertz D. Time delay estimation by generalized cross- correlation methods[J].,, 1984, 32(2): 280-285.

[18] Benesty J, Jingdong C, and Yiteng H. Time-delay estimation via linear interpolation and cross correlation[J]., 2004, 12(5): 509-519.

[19] Pertilä P, Korhonen T, and Visa A. Measurement combination for acoustic source localization in a room environment[J].,,, 2008, 3: 1-14.

[20] Dermatas S, Fakotakis D, and Kokkinakis K. Fast endpoint detection algorithm for isolated word recognition in office environment[C]. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing, Toronto, Canada, 1991：733-736.

[21] 郭胜楠, 崔慧娟, 唐昆. 低信噪比下基于短时谱估计的语音增强[J]. 清华大学学报(自然科学版), 2010, 50(1): 149-152.

Guo Sheng-nan, Cui Hui-juan, and Tang Kun. Speech enhancement based on short time spectral amplitude estimates in low SNR[J].(), 2010, 50(1): 149-152.

[22] 李志舜. 鱼雷自导信号与信息处理[M]. 西安: 西北工业大学出版社, 2004: 138-144.

Improved Multiple Signal Classification Algorithm for Direction of Arrival Estimation Based on Covariance Matrix of Cross-correlation

Mao Lin-lin Zhang Qun-fei Huang Jian-guo Shi Wen-tao Han Jing

(,,’710072,)

In view of the poor performance of traditional Direction of Arrival (DOA) methods at low signal-to-noise ratios, an improved MUltiple SIgnal Classification (MUSIC) algorithm for DOA estimation applied to active detection system based on covariance matrix decomposition of cross-correlation (I-MUSIC) is proposed. Exploiting the transmission feature of active sonar, cross-correlation sequence between the transmitted signal and the array output is formulated. The spatial covariance matrix is then constructed from the sequence. Then matrix decomposition is implemented over the new spatial covariance matrix to estimate the DOA. It is proved that cross-correlation can suppress noise while preserving the phase information between array elements, which facilitate the subspace separation at low SNRs. Furthermore, another novel method based on correlation Time threshold (T-MUSIC) is proposed to further improve the DOA performance. Simulation results indicate thatI-MUSIC and T-MUSIC can obtain a performance gain of 3 dB and 6 dB, with the estimate error being 77% and 53% of the original method respectively. Due to data selection via time threshold, T-MUSIC is not appreciably affected by noise, and thus outperforms IM-MUISC for 8 dB at low SNRs. I-MUSIC and T-MUSIC can improve the DOA performance at low SNRs significantly if applied to active multi-target detection system.

Signal processing; Direction of Arrival (DOA) estimation; Cross-correlation; Covariance matrix; MUltiple SIgnal Classification (MUSIC)

TN911.7

A

1009-5896(2015)08-1886-06

10.11999/JEIT141208

毛琳琳 maple3511@mail.nwpu.edu.cn

2014-09-17收到，2015-04-16改回，2015-06-09网络优先出版

国家自然科学基金(61271415)资助课题

毛琳琳： 女，1991年生，博士生，研究方向为水下信号处理.

张群飞： 男，1968年生，教授，研究方向为水下信息处理、水声通信和系统仿真.

黄建国： 男，1945年生，教授，研究方向为现代信号处理、阵列信号处理.