基于半正定约束的极化相似度最优模型匹配目标分解

范庆辉 卢红喜 保 铮 肖春宝



基于半正定约束的极化相似度最优模型匹配目标分解

范庆辉*①②卢红喜③保 铮③肖春宝①②

①(西安电子科技大学计算机学院 西安 710071)②(河南科技大学信息工程学院 洛阳 410023)③(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

目标分解是实现极化合成孔径雷达目标分类、检测与识别应用的重要手段。传统方法由于优先对体散射分量进行提取，其体散射能量的高估或二面角散射能量的低估现象较为严重。该文通过引入极化相似度量，基于数据驱动自适应地对基本散射机制的最优匹配模型进行选择。在此基础上，根据极化相似度量确定基本散射机制散射能量提取的优先顺序，并以各阶次剩余矩阵能量非负为约束，最终确定面散射、二面角散射、体散射这3种基本散射机制的能量贡献值。实测数据处理结果及其与光学图像的对比结果表明，该文方法获取的极化目标分解结果优于传统方法，能够准确地提取目标区域的基本散射特征。

极化合成孔径雷达；目标分解；极化相似度；最优模型匹配

1 引言

随着极化和高分辨测量技术的发展，分辨单元越小，它包含的散射中心的数目就越少，对目标结构特性的刻画就越细致清晰，将极化与高分辨技术结合的雷达识别技术成为复杂目标识别的一个重要分支。极化合成孔径雷达(Polarimetric SAR, PolSAR)通过测量地面每个分辨单元内的散射回波，经过成像处理获取对应的散射矩阵，极化散射矩阵将目标散射能量特性、相位特性及极化特性统一起来，相对完整地描述了雷达目标的电磁散射特性[6,7]。从极化SAR图像数据中可以提取目标的极化散射特性，实现全极化SAR目标的分类、检测与识别等应用。

极化目标分解方法是有效提取目标极化散射特性的一类重要方法。现有的极化目标分解方法主要有相干目标分解和非相干目标分解两类。非相干目标分解方法一般基于参数模型进行展开，例如Freeman-Durden分解方法[11,12]，Yamaguchi分解方法[13,14]，基于非负特征值约束的模型分解方法[15]等。在这些方法中，相干矩阵被分解为几种不同散射机制散射机理的叠加，通常主要考虑面散射，二面角散射，体散射，螺旋体散射等[12]。这些分解方法通常在首先计算体散射机制对应的散射能量，然后计算面散射与二面角散射机制对应的散射能量。这实质上是将体散射机制置于优先分解的位置上，可能会导致体散射能量的高估及负能量的出现，同时也会导致在二面角散射机制或面散射机制占主导的地区，面散射或二面角散射能量的低估。本文方法基于极化相似度匹配度量准则，研究了全极化SAR单视及多视实际观测数据中基本散射机理的分离，通过引入极化相似度确定不同散射机制的分解次序并自适应地选取匹配模型，解决现有方法中体散射能量的高估或二面角散射能量的低估问题，从而完成模型参数估计与散射能量的有效估计。实测数据处理结果及其与光学图像的对比结果表明，本文方法能够准确地提取目标区域的基本散射特征。

2 极化目标分解方法基本理论

通过分析极化数据提取目标的散射特性，其理论核心就是极化目标分解。大多数自然场景目标或分布目标为非相干目标，其散射特性可以是非确定或时变的，极化SAR系统观测的各次散射回波非相干或部分相干。同时考虑到相干斑噪声的影响，非相干目标需用不低于二阶的统计量进行描述，如极化协方差矩阵或相干矩阵[16]。通过非相干目标分解方法从极化SAR观测数据中提取各个基本散射机制贡献分量的经典理论模型[17]可表示为

现有非相干目标极化特性分解方法的主要区别在于各散射机制能量贡献的提取方法及其模型参数求解策略。本文通过引入极化相似度量，基于数据驱动自适应地对基本散射机制的最优匹配模型进行选择；在此基础上，根据极化相似度量确定出基本散射机制散射能量提取的优先顺序，并以各阶剩余矩阵能量非负为约束，最终确定出面散射、二面角散射、体散射这3种基本散射机制的能量贡献值。

3 基于极化相似度模型匹配的目标分解方法

本节首先介绍基于极化相似度模型匹配目标分解方法的基本原理，并在此基础上对本文提出的基于极化相似度模型匹配的目标分解方法具体实施步骤进行详细展开。

3.1基于极化相似度模型匹配的目标分解方法基本原理

现有极化目标分解方法通常优先对体散射机制进行分离再分解其他散射机制，针对这些方法存在的体散射能量高估现象，本文以极化相似度量为准则自适应地完成参数模型匹配，并以此确定各基本散射机制的分解顺序。对于实际观测得到的相干矩阵，参数化模型的极化目标分解方法极容易受目标方位取向角的影响[13]，因此在应用极化目标分解方法前必须予以去除。在此基础上，各个基本散射机制的分解顺序以极化相似度量值为依据，在各散射机理相干矩阵半正定的约束下，依次提取出各散射机理的最大能量贡献分量。在各基本散射机理分量提取完毕之后，计算出最终残余矩阵与各基本散射机理之间的极化相似度大小，并以此为依据对其散射机理类型归属进行判别，最终得到各基本散射机理对观测相干矩阵的能量贡献。

3.2本文算法基本流程

下文分别以8个步骤来对本文方法进行展开，详细讲述各个步骤实现的具体方法。

步骤1 方位取向角去除 首先根据获取的全极化SAR图像数据计算出每个像素点对应的相干矩阵，并对其方位取向角进行估计与去除，得到零方位取向角下的相干矩阵。方位取向角的估计方法为[13,17]

步骤2 第1散射机制确定及其相干矩阵模型参数估计 考虑3种基本的散射机制，即面散射机制、二面角散射机制及体散射机制。计算与面散射机制对应的相干矩阵，二面角散射机制对应的相干矩阵及体散射机制对应的相干矩阵之间的最大极化相似度，确定相干矩阵的第1散射机制及其对应的相干矩阵。

步骤3 第1散射机制能量贡献与剩余矩阵计算。

由二阶主子式非负可得

步骤4 第2散射机制确定及其相干矩阵模型参数估计 对已提取出第1散射机制的剩余矩阵，采用步骤2的方法计算其与去除第1散射机制后的剩余两种散射机制之间的最大极化相似度，确定的主导散射机制为第2散射机制，并对其相干矩阵的模型参数进行估计。

步骤5 第2散射机制能量贡献与剩余矩阵计算 根据上述步骤得到的及，在剩余矩阵能量非负的约束下，计算第2散射机制对应的散射能量，重新计算并更新剩余矩阵为。

步骤6 第3散射机制相干矩阵模型参数估计、能量贡献及剩余矩阵计算 采用步骤2的方法计算与去除第1、第2散射机制后的最后剩余散射机制(记为第3散射机制)之间的最大极化相似度，确定第3散射机制对应的相干矩阵。由与，在剩余矩阵能量非负的约束下，采用步骤5的方法计算第3散射机制对应的散射能量及剩余矩阵。

步骤7 剩余矩阵散射机制类型归属确定 采用步骤2的方法计算与3种散射机制之间的最大极化相似度，确定的主导散射机制，将对应的能量归于该主导散射机制对应的散射能量上。

步骤8 各个基本散射机制散射能量的确定 根据第1散射机制，第2散射机制和第3散射机制对应的散射类型，确定当前像素点对应地面单元的面散射机制对应的能量，二面角散射机制对应的能量及体散射机制对应的能量。

4 实验与结果分析

本节试验分别采用机载和星载极化SAR数据对本文算法的性能进行分析。第1组为2005年10月AIRSAR机载系统获取的San Francisco的全极化SAR 4视数据，第2组为2008年6月Radarsat2星载系统获取的日本东京地区的全极化SAR单视数据。试验区域图像的像素大小为。试验中分别采取van Zyl提出的非负特征值约束分解方法(NNED)与本文所提基于极化相似度模型匹配的目标分解方法对上述两组全极化SAR数据进行目标分解处理。在San Francisco地区的全极化SAR 4视数据中，选择6个不同的试验区域图像，如图1所示。图2为利用本文方法得到的极化目标分解结果，图3为利用NNED方法得到的分解结果。为了定量对两种方法的数据处理结果进行分析，表1中给出了图1所示的每一个试验区域图像分解结果中各个散射机制所占能量的百分比(在表1的拼图中，深灰色代表二面角散射机制所占能量，浅灰色代表体散射机制所占能量，黑色代表面散射机制所占能量，并采用向下取整方式显示各个分量所占整体的百分比，下同)。

图1 San Francisco地区Google Earth光学图像

图2 本文方法分解结果

图3 NNED方法分解结果

表1 San Francisco数据不同分解方法下各散射机制所占百分比

如图1所示的区域1和区域3，由光学图像可知该试验区域图像为城市建筑区。对于城市建筑区，二面角散射机制占主导，且二面角散射能量所占比例越高，越利于后续的检测识别。由表1可知，非负特征值约束下区域1中二面角散射机制所占能量比例为59%，采用本文方法区域1中二面角散射机制所占能量比例为69%；非负特征值约束下区域3中二面角散射机制所占能量比例为39%，而采用本文方法区域3中二面角散射机制所占能量比例为49%。由此可见，利用本文分解方法获取的城市地区主导散射机制能量比例优于NNED方法。在区域2与区域4中，由图1中光学图像可知该试验区域图像对应于森林植被区，本文方法与NNED方法的分解结果中体散射机制所占能量比例相差不大，均表现为体散射机制占主导，与真实结果相一致。区域5对应为裸露山区，其面散射为主导散射机制，本文方法得到的分解结果中面散射机制能量比例也高出NNED方法结果近10%；而对于区域6对应的海面区域，本文方法与NNED方法获取的结果相当。

在东京地区的全极化SAR单视数据中，选择4个不同的试验区域图像，如图4所示。图5为利用本文方法得到的该数据极化目标分解结果，图6为利用NNED方法得到的分解结果。针对单视数据的情况，按照两种方法进行数据处理的定量分析结果如表2所示。

图4 日本东京地区Google Earth光学图像

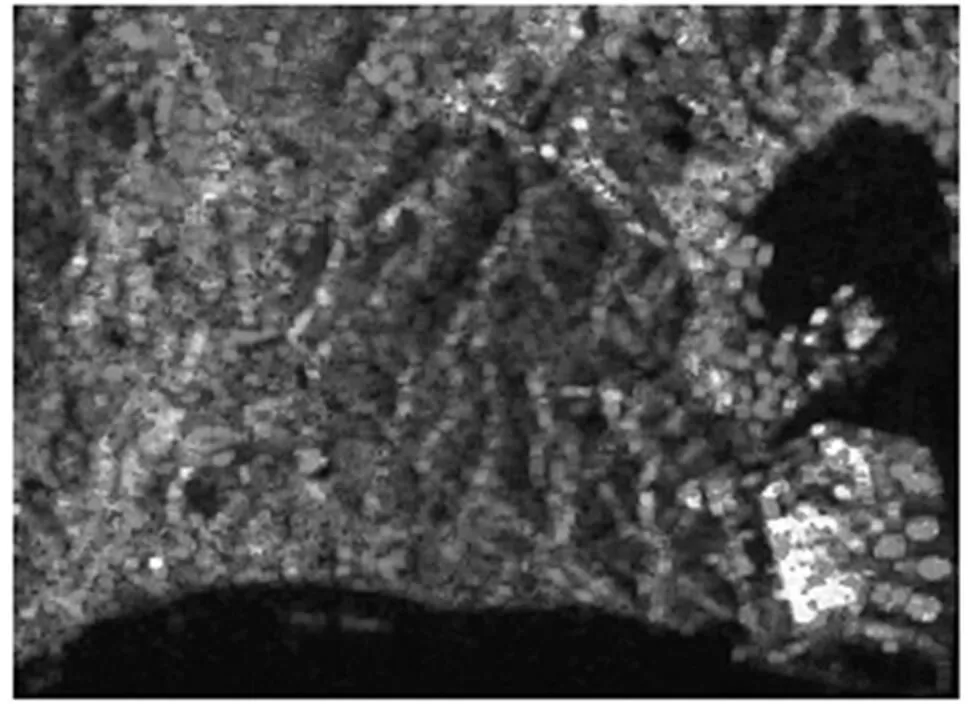
图5 本文方法分解结果

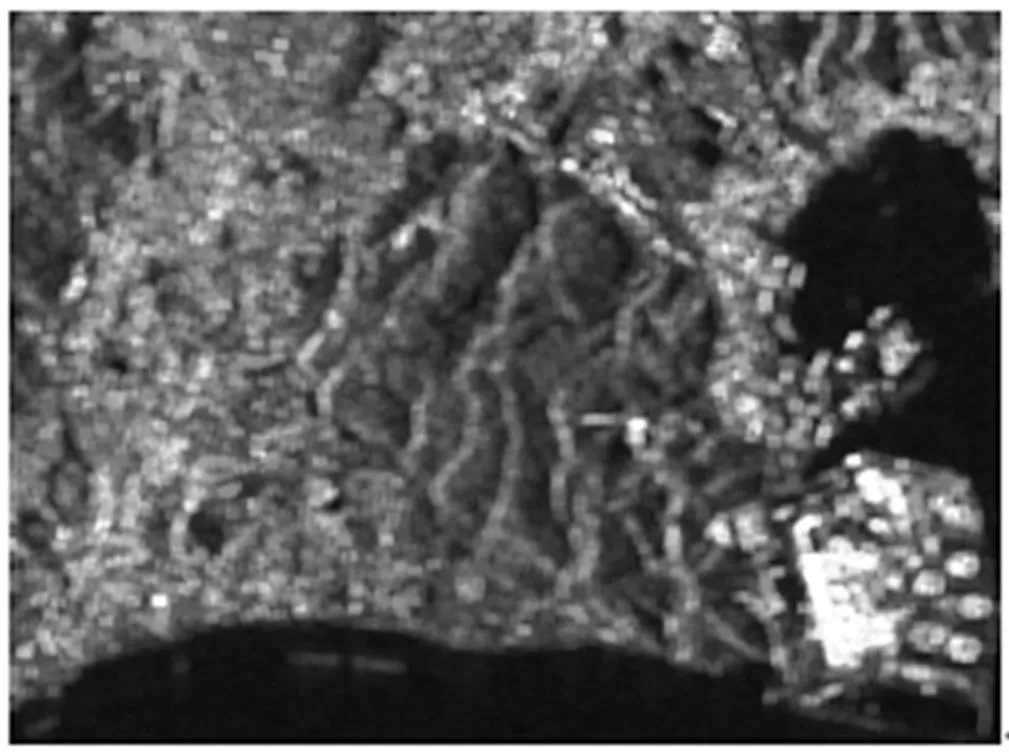
图6 NNED方法分解结果

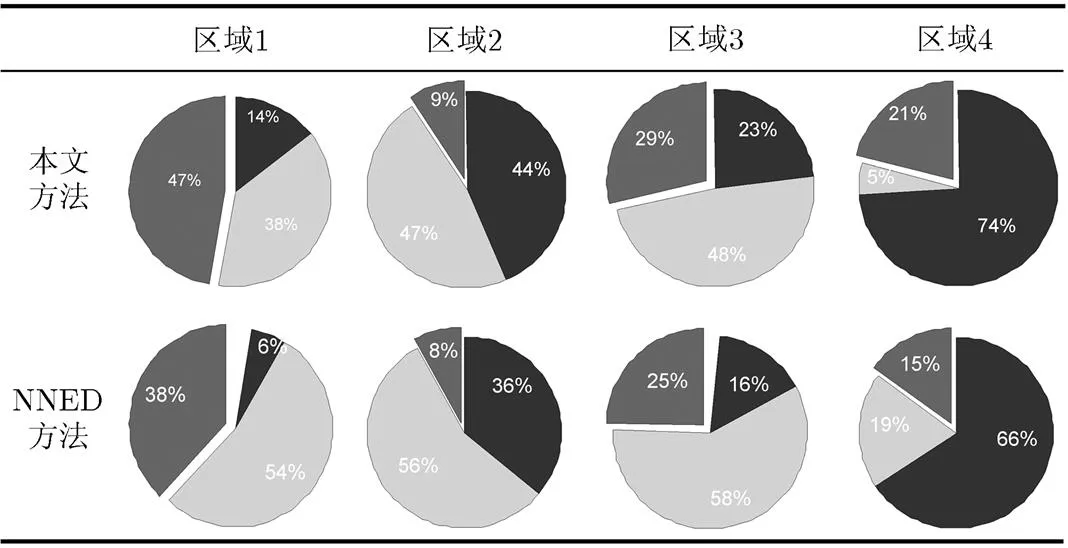
表2对日本数据不同极化分解方法下个散射机制所占比例

表2列出了东京地区数据所选子区域中各个散射机制所占百分比。对于图4中的区域1，由光学图像可知该子区域为某发电厂地区，其人工建筑特征明显(即二面角散射机制占主导)。如表2所示，在非负特征值约束下区域1中二面角散射机制所占能量比例为38%，而采用本文方法其二面角散射机制所占能量比例为47%。对于区域3区域，由光学图像可知该区域对应倾斜的城市建筑，由NNED方法得到的二面角散射机制所占能量比例为25%，而采用本文方法区域3中二面角散射机制所占能量比例为29%。由此可见，本文方法所提取的城市地区二面角散射机制对应的能量比例优于NNED的方法。由光学图像可知，区域2对应区域为裸露河床，其大部分像素是二面角散射与面散射机制占主导，仅仅是子图周边区域存在一定的体散射过程。本文方法二面角与面散射机制两者之和为53%，远远高于NNED方法的44%，可见本文方法能够较为准确地提取出河床地表的散射机制。区域4对应为海湾区域，很明显其面散射机制占主导，而体散射机制最弱，考虑到海湾水面的波澜起伏，其二面角散射分量明显会高于体散射分量。从实验处理结果可以看出，本文方法与NNED方法相比能够准确地提取出海湾区域的散射机理。

5 结束语

本文针对传统极化目标分解算法的缺陷，通过引入极化相似度量最优化极化目标分解策略。该文基于数据驱动自适应地对各个基本散射机制的最优匹配模型进行选择；在此基础上，根据极化相似度量确定出基本散射机制散射能量提取的优先顺序，并以各阶次剩余矩阵能量非负为约束，最终确定出面散射、二面角散射、体散射这3种基本散射机制的能量贡献值；解决了传统方法优先对体散射分量进行提取而导致的体散射能量高估或二面角散射能量低估问题。实测数据处理结果及其与光学图像的对比结果表明，该文方法获取的极化目标分解结果优于传统方法，能够准确地提取目标区域的基本散射特征。

参考文献

[1] Boerner W M, Yan W L, Xi A Q,Basic Concepts of Radar Polarimetry[M]. Netherlands: Springer, 1992: 155-245.

[2] Boerner W M. Basics of SAR Polarimetry I[R]. Chicago, IL: 2007.

[3] Mott H. Remote Sensing with Polarimetric Radar[M]. New York: Wiley-IEEE Press, 2007: 3-19.

[4] Cloude S R. Polarisation: Applications in Remote Sensing[M]. Oxford: Oxford University Press, 2009: 4-103.

[5] Lee J S and Pottier E. Polarimetric Radar Imaging From Basics to Applications[M]. United States: CRC Press, 2009: 5-53.

[6] Zebker H A and van Zyl J J. Imaging radar polarimetry: a review[J]., 1991, 79(11): 1583-1606.

[7] Chen Q, Kuang G Y, Li JUnsupervised land cover/land use classification using PolSAR imagery based on scattering similarity[J]., 2013, 51(3): 1817-1825.

[8] Frery A C, Cintra R J, and Nascimento A. Entropy-based statistical analysis of PolSAR data[J]., 2013, 51(6): 3733-3743.

[9] Kajimoto M and Susaki J. Urban-area extraction from polarimetric SAR images using polarization orientation angle[J]., 2013, 10(2): 337-341.

[10] Zhang P, Li M, Wu YUnsupervised multi-class segmentation of SAR images using fuzzy triplet Markov fields model[J]., 2013, 46(4): 1-16.

[11] Ballester-Berman J D and Lopez-Sanchez J M. Applying the Freeman-Durden decomposition concept to polarimetric SAR interferometry[J]., 2010, 48(1): 466-479.

[12] Freeman A and Durden S L. A three-component scattering model for polarimetric SAR data[J]., 1998, 36(3): 963-973.

[13] Yamaguchi Y, Sato A, Sato RFour-component scattering power decomposition with rotation of coherency matrix[J]., 2011, 49(6): 2251-2258.

[14] Yamada H, Komaya R, Yamaguchi Y,Scattering component decomposition for POL-InSAR dataset and its applications[C]. Geoscience and Remote Sensing Symposium, Cape Town, 2009: V-154-V-157.

[15] Van Zyl J J, Arii M, and Kim Y. Model-based decomposition of polarimetric SAR covariance matrices constrained for nonnegative eigenvalues[J]., 2011, 49(9): 3452-3459.

[16] Cloude S R and Pottier E. A review of target decomposition theorems in radar polarimetry[J].,1996, 34(2): 498-518.

[17] Singh G, Yamaguchi Y, and Park S E. General four- component scattering power decomposition with unitary transformation of coherency matrix[J]., 2013, 51(5): 3014-3022.

Positive-semidefinite Based Target Decomposition Using Optimal Model-matching with Polarization Similarity

Fan Qing-hui①②Lu Hong-xi③Bao Zheng③Xiao Chun-bao①②

①(,,’710071,)②(,,410023,)③(,,’710071,)

Target decomposition is an important tool to realize target classification, detection and recognition applications with Polarimetric SAR (PolSAR). However, the traditional method with priority of volume scattering component extraction seriously performs overestimation in the volume scattering energy or underestimation in the dihedral scattering energy. In this paper, by introducing polarimetric similarity measure, data-driven model- matching for basic scattering mechanism is proposed. On this basis, the priority of scattering mechanisms energy extraction is determined with the similarity measure. Based on the non-negative constraint of energy, all the orders of residual matrix are reextracted for the final energy contribution of the dihedral scattering, volume scattering, and surface scattering mechanism. The processing results of real data and their comparison with the optical image results show that the proposal is better than traditional methods for the accurate extracttion of the basic scattering characteristics in the targets region.

Polarimetric SAR (PolSAR); Target decomposition; Polarization similarity; Optimal model matching

TN957.51

A

1009-5896(2015)08-1821-07

10.11999/JEIT141468

范庆辉 haustfanqh@126.com

2014-11-24收到，2015-04-24改回，2015-06-09网络优先出版

国家自然科学基金(61271024, 61201292, 61201283)，新世纪优秀人才支持计划(NCET-09-0630)，全国优秀博士学位论文作者专项资金(FANEDD-201156)，省部级基金和中央高校基本科研业务费专项资助课题

范庆辉： 男，1978年生，博士生，研究方向为雷达目标识别、纠错码、嵌入式系统等.

卢红喜： 男，1987年生，博士生，研究方向为极化SAR/InSAR、多基线InSAR信号处理、阵列优化设计与极化层析成像技术研究.

肖春宝： 男，1976年生，博士生，研究方向为雷达目标识别、计算机视觉等.