基于亚区结构的人体二尖瓣的建模与仿真

赵晓佳,宋 晓,黄晓阳*,苏茂龙,钟 琪

(1.厦门大学信息科学与技术学院,福建 厦门361005;2.南阳师范学院计算机与信息技术学院,河南南阳473061;3.厦门大学附属中山医院超声医学科,福建厦门361004)

基于亚区结构的人体二尖瓣的建模与仿真

赵晓佳1,宋 晓2,黄晓阳1*,苏茂龙3,钟 琪1

(1.厦门大学信息科学与技术学院,福建 厦门361005;2.南阳师范学院计算机与信息技术学院,河南南阳473061;3.厦门大学附属中山医院超声医学科,福建厦门361004)

通过建立精细的人体二尖瓣有限元模型,仿真前后瓣叶厚度不均匀的二尖瓣模型在心脏收缩初期的动态闭合过程,与前后瓣叶厚度均匀的二尖瓣模型的仿真结果相比较.仿真结果表明:两种模型的瓣叶应力分布不均匀,最大应力值都出现在后瓣叶亚区与亚区之间的裂口位置,与临床二尖瓣撕裂常发生位置一致,表明了仿真方法以及结果的正确性,瓣叶厚度不均匀模型中瓣叶应力水平相对较低,更符合实际.最后根据临床数据,设置厚度不均匀模型中瓣环与乳头肌的二维运动,再次进行仿真.仿真结果表明该精细模型瓣叶的闭合度比之前瓣环与乳头肌固定不动模型的闭合度高,瓣叶应力分布相对较均匀,更接近实际生理情况,为后续的病理等的仿真奠定了基础.

二尖瓣;有限元模型;应力分布;最大应力

二尖瓣是人体心脏的重要瓣膜组织之一,它位于左心房与左心室之间,由二尖瓣环、两个瓣叶、腿索、乳头肌等结构组成[1].二尖瓣的瓣叶分为较大的前瓣叶和较小的后瓣叶,后瓣叶可细化为3个较窄的亚区结构[2]:P1、P2、P3.二尖瓣的瓣叶与瓣环、腿索相连,腿索又与乳头肌相连.根据Lam等[3]的分类方式将腿索分为3级:1级腿索连接于瓣叶的游离缘,2级腿索连接于瓣叶的粗糙部,3级腿索从室壁连接到后瓣叶的基底部.二尖瓣维持正常的生理职能,需要各个组成结构的完整、乳头肌的正常收缩及腿索的牵引[4].

二尖瓣的生物力学是一个复杂的问题:结构体的大变形,瓣膜组织的各向异性的非线性弹性行为以及心动周期内的血液动力学的载荷等.建模仿真是分析瓣膜功能有效性的技术方法.随着科技的发展、仿真技术的不断完善,人们可以对瓣膜功能有更加精确的了解,可以选择更适合的病理治疗方式.通过对人体二尖瓣进行建模仿真,可以更好地认识二尖瓣的力学机理,对后期分析二尖瓣关闭不全等病理结构以及指导瓣膜修复术具有重要的意义.

目前关于二尖瓣的研究分为结构模型和流固耦合模型两类.结构模型是指模型中只有二尖瓣的结构组件,不考虑血液;流固耦合模型是指二尖瓣的结构与血液流体域相互作用的模型,它主要研究二尖瓣结构在流体作用下的各种行为以及结构对流体域的影响.其中结构模型是流固耦合模型的基础,主要研究的学者有Kunzelman团队[5-7]、Lim团队[8]等.Kunzelman等[5]建立了最原始的人体二尖瓣模型,模拟了二尖瓣的闭合过程.Lim等[8]建立厚度均匀的膜结构瓣叶,模拟正常二尖瓣工作机理,但该模型中瓣叶自由边上无尖端,忽略了瓣叶形态的局部细节.Kunzelman等[7]、罗云等[9]将二尖瓣的后瓣叶简化为1个瓣尖,成功模拟出瓣叶的开闭过程,但并未根据实际生理情况将后瓣叶分为3个亚区.这些研究都没有模拟瓣环与乳头肌的二维运动过程.本文研究的目的,就是为了比较更加精细的模型对仿真结果的影响.

本文根据人体二尖瓣的实际生理结构,以二尖瓣的亚区结构特征,建立比较精细的二尖瓣三维有限元模型:后瓣叶分为3个亚区结构,腿索分为游离边缘腿索,粗糙带以及基底部腿索.二尖瓣瓣膜厚度分为两种情况:1)前后瓣叶厚度相同的厚度均匀模型; 2)前后瓣叶厚度不相同的厚度不均匀模型.两种模型分别模拟其瓣叶在心脏收缩初期心房心室压力差的作用下的闭合过程,并比较了两种仿真模型的差异.在瓣叶厚度不均匀的模型基础上,按照临床数据及相关描述,设置瓣环与乳头肌的二维运动过程,更加精细地模拟二尖瓣的闭合过程.

1 方 法

采用ANSXS建立二尖瓣有限元模型,并用LSDXNA求解器进行求解,得到二尖瓣模型的应力随时间的变化的结果,用LS-PREPOST后处理器生成可视化结果.

1.1 二尖瓣几何模型

二尖瓣模型由瓣环、瓣叶、腿索和乳头肌组成.本文根据文献[3,10-11]建立的模型如图1所示:xy平面的瓣环呈D字,乳头肌简化为2个固定的点,瓣叶从瓣环向z轴正方向延伸,后瓣叶细分为3个亚区结构.与瓣叶游离边缘相连的腿索有24根,与后瓣叶基底部相连的腿索有2根,与粗糙带相连的腿索分支有18根.

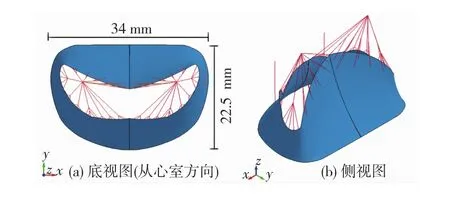
图1 人体二尖瓣几何模型Fig.1 Geometric model of human mitral valve

1.2 物理性质

二尖瓣的所有组织均设置为各向同性的弹性材料.瓣叶密度为1 040 kg/m3[10],泊松比设置为0.45,弹性模量设置为4 MPa[12];腿索的密度为1 040 kg/ m3[10],其应力-应变曲线如图2所示[13].

1.3 网格划分

在ANSXS中对二尖瓣模型进行网格划分,采用自由网格划分,共划分为4 396个Belytschko壳单元;腿索横截面积均设置为0.4 mm2[14],共划分为760个桁架单元.模型中瓣膜的厚度分2种情况讨论:1)瓣叶厚度均匀的模型:前后瓣叶厚度均设置为1.3 mm; 2)前后瓣叶厚度不相同的厚度不均匀模型:根据文献[15-16],前瓣叶厚度设置为1.32 mm,后瓣叶厚度设置为1.26 mm.两种情况下的网格划分方式一样,仅前后瓣叶厚度不同.

图2 二尖瓣腿索材料应力-应变曲线Fig.2 Stress-strain behavior of mitral valve chordae tendineae

1.4 边界与负载条件

基于二尖瓣的面对称结构,在对称面上节点x轴方向位移为0.二尖瓣瓣环与乳头肌在整个心动周期内的位置相对固定,因此假设瓣环和乳头肌固定不动,瓣环上节点的位移为0.

左心室与左心房在单个心动周期内压力值的临床数据[17]如图3所示,由于二尖瓣在心脏收缩初期压力斜坡(early systolic pressure ramp,ESPR)区,瓣膜载荷会随着时间动态增长至最大值,此时的二尖瓣较容易出现应力集中现象,因此着重研究ESPR区瓣膜的应力分布情况.通过测量图3上同一时刻心室与心房的压强,然后求得它们之间的差值即左心室房压强差,这个左心室房压强差就是施加在二尖瓣上的动态载荷,如图4所示.

图3 心室心房压力曲线Fig.3 Atrial and ventricular pressure profiles

2 结 果

2.1 二尖瓣瓣叶闭合

分别模拟两种模型在ESPR区二尖瓣瓣叶的闭合情况,仿真结果如图5所示.

由图5可知,2个模型中的瓣叶均在左房室压差以及腿索的共同作用下慢慢对合,最终实现前后瓣叶的接触.两个模型中瓣环的形状没有发生变化,模型的闭合程度基本一样,无显著差异.

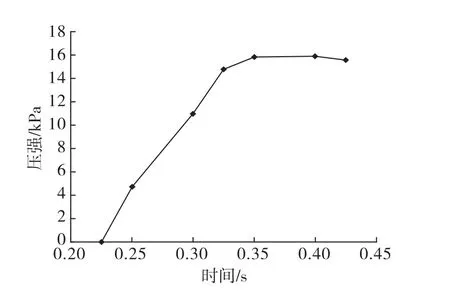
图4 二尖瓣载荷曲线Fig.4 Transvalvular pressure load applied to the mitral valve

图5 二尖瓣瓣叶闭合情况Fig.5 Configuration of the valve at closure

2.2 二尖瓣瓣叶应力分布

分别对二尖瓣在ESPR区应力分布进行仿真,对应的最大von Mises应力分布如图6所示.

如图所示,在ESPR区400 ms时刻,左房室压差趋于稳定,约16 k Pa,两个模型的二尖瓣von Mises应力均达到最大,最大应力值均出现在亚区的裂口位置,与临床上瓣叶容易撕裂的位置一致[18],与钟琪等[19]的结果一致.表1列出了两种模型的仿真结果对比情况.两个模型应力分布都不太均匀,均出现了应力集中现象,两个模型除了后瓣叶亚区间应力最大外,前后瓣叶以及瓣叶与瓣环连合处的von Mises应力也都比较大,但厚度不均匀模型的总体von Mises应力水平比厚度均匀模型的von Mises应力水平低,更不容易出现撕裂的状况,与实际生理相符.

表1 2种模型仿真结果对比Tab.1 Comparison of the results between two models

2.3 瓣环和乳头肌的运动

根据文献[20-23]对瓣环运动的描述,瓣环在xy平面的移动可以描述为:1)前瓣环长度增加11%,但是瓣环总长度缩短13%;2)瓣环横向长度(即x轴长度)增加5%.

根据文献[16]描述,以及整个ESPR区,瓣环与乳头肌的位置是相对不动,乳头肌沿x轴朝着前后瓣叶连合处移动0.85 mm,沿y轴朝着前瓣叶方向移动1.10 mm.

在厚度不均匀模型基础上,仿真瓣环以及乳头肌在xy平面的移动以及瓣叶的闭合过程,仿真结果如图7所示.

图6 400 ms时刻瓣叶最大von Mises应力分布图Fig.6 Maximum von Mises stress distribution on the valve leaflets at 400 ms

如图7所示,ESPR区初期,二尖瓣的von Mises应力比较低,左心房室的压力差约为0 kPa;在300 ms时刻,左心房室的压差约为10 kPa,二尖瓣的von Mises应力分布在0.042～0.253 MPa之间;在375 ms时刻,左心房室压差约为16 kPa,二尖瓣的von Mises应力主要在0.047～0.280 MPa,腿索与后瓣叶的连接处及前后瓣叶连合处出现应力集中现象;在425 ms时刻,左心房室压差约为16 kPa,二尖瓣的von Mises应力分布在0.048～0.291 MPa,基底腿索与后瓣叶的连接处及前后瓣叶连合处出现应力集中现象.总体看,二尖瓣瓣环在整个ESPR区的von Mises应力分布相对比较均匀,最大von Mises应力集中在腿索与瓣叶的连接处以及前后瓣叶之间的连合处,最大应力值为0.485 MPa.在二尖瓣瓣叶的闭合过程中,二尖瓣瓣环的形态发生了很大的变化,由原来的D字形变成了一个类似椭圆形,瓣环在x轴方向长度变长,y轴方向长度缩短.除了形态的变化,瓣叶的闭合度也明显发生了变化,与原先厚度不均匀模型相比,瓣叶的闭合程度明显提高,与实际生理情况符合,如表2所示.

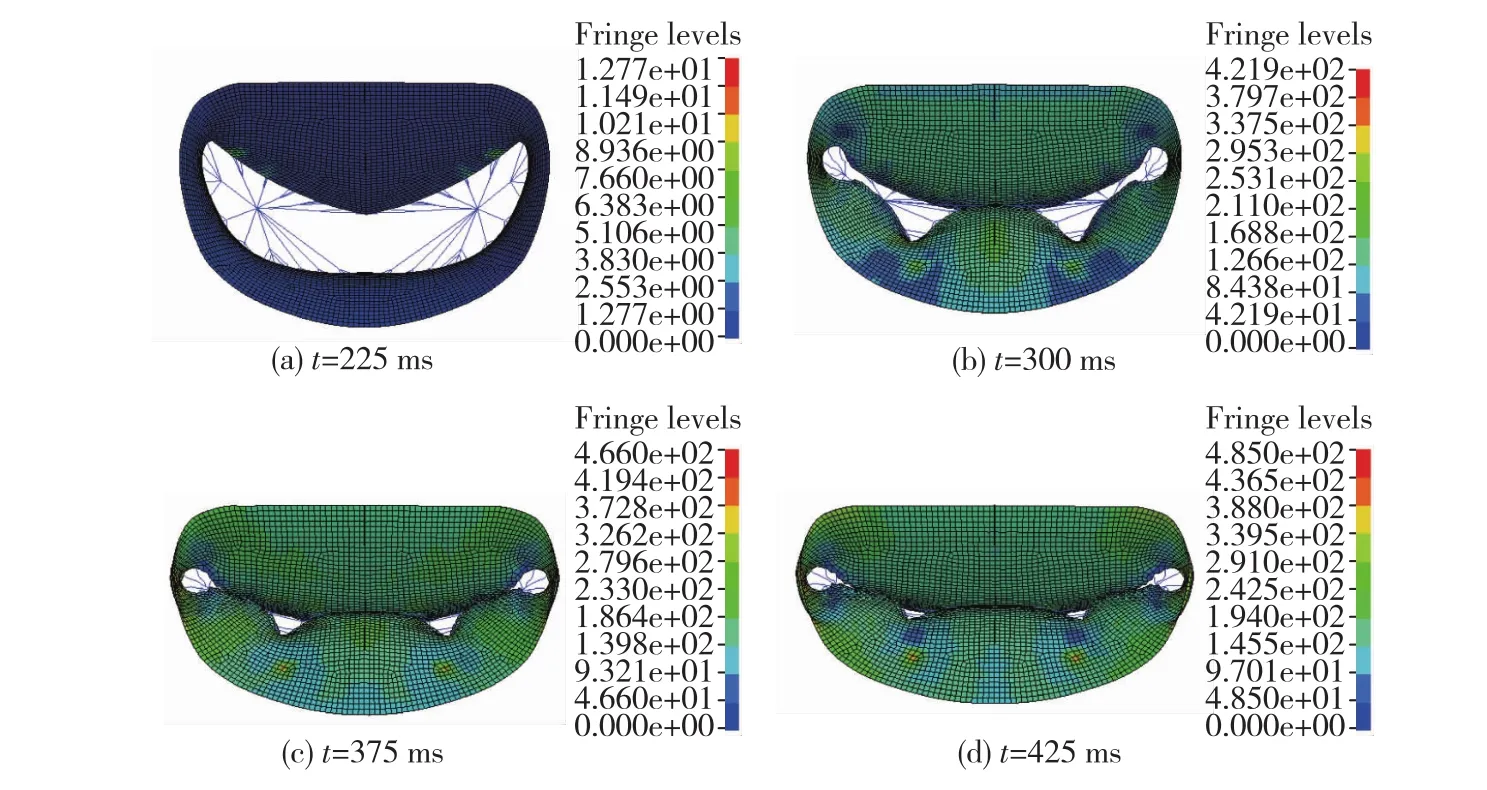
图7 不同时刻二尖瓣瓣叶von Mises应力分布图Fig.7 von Mises stress distribution on the valve leaflets at different time

表2 瓣环与乳头肌的运动对仿真结果的影响Tab.2 Impact of annulus and papillary muscles movement to the simulation results

3 结 论

为了研究比较精细模型对仿真结果的影响,本文参照实际生理结构,将二尖瓣的后瓣叶细分为3个亚区,建立了瓣膜厚度分布均匀和分布不均匀2种模型,对二尖瓣瓣叶在ESPR区的闭合过程进行了仿真.仿真结果表明,在整个ESPR区,瓣膜应力最大值出现在400 ms左右,位置在P2亚区与P1、P3亚区的裂口位置,此时心房心室的压力差最大,约16 k Pa.厚度不均匀模型的应力水平比较低,不易出现撕裂现象,更接近实际的生理情况.在此基础上,本文根据实际生理情况,设置瓣环与乳头肌的运动,再次仿真瓣叶的闭合过程,仿真结果显示前后瓣叶的连合处及腿索与后瓣叶连接处应力较大,仿真的结果与临床二尖瓣撕裂研究[18]相符合,同时与Kunzelman等[14]的模拟结果接近,前瓣叶的最大应力值略小一些,约为0.300 MPa,后瓣叶的应力值均约为0.200 MPa.瓣叶的闭合度更高,更符合实际生理情况.本文研究结果表明,建立瓣膜厚度不均匀模型,并在仿真过程中设置瓣环与乳头肌的运动,仿真模型及过程更符合人体真实二尖瓣情况,仿真结果也更接近临床数据,更适合后续二尖瓣病理情况的仿真与分析.

瓣叶实际材料属性是非线性各向异性的,本文瓣叶简化为线性各向同性,以后的研究将细化瓣叶属性.血液的流动对二尖瓣的行为产生影响,二尖瓣瓣膜在血液影响下的流固耦合运动情况将是后续值得深入研究的一个方向.

[1] 冯敏,黄晓阳,苏茂龙,等.基于双弹性腔的左心循环系统的建模与仿真[J].厦门大学学报:自然科学版,2012,51 (4):676-681.

[2] Dominik J,Zacek P.Heart valve surgery:an illustrated guide[M].Berlin:Spring-Verlag,2010:10-11.

[3] Lam J H,Ranganathan N,Wigle E D,et al.Morphology of the human mitral valve:Ⅰ.Chordae tendinese:a new classification[J].Circulation,1970,41(3):449-458.

[4] 黄化清.二尖瓣腿索断裂[J].临床心血管病杂志,1985,1 (1/2):80-83.

[5] Kunzelman K S,Cochran R P,Chuong C,et al.Finite element analysis of the mitral valve[J].J Heart Valve Dis, 1993,2:326-340.

[6] Kunzelman K S,Cochran R P,Verrier E D,et al.Anatomic basis for mitral valve modeling[J].J Heart Valve Dis, 1994,3:491-496.

[7] Kunzelman K S,Einstein D R,Cochran R P.Fluid-structure interaction models of the mitral valve:function in normal and pathological states[J].Philosophical Transactions of the Royal Society B:Biological Sciences,2007, 362(1484):1393-1406.

[8] Lim K H,Xeo J H,Duran C.Three-dimensional asymmetrical modeling of the mitral valve:a finite element study with dynamic boundaries[J].J Heart Valve Dis, 2005,14:386-392.

[9] 罗云.二尖瓣有限元建模与生物力学分析[D].厦门:厦门大学,2014.

[10] Lau K D,Diaz V,Scambler P,et al.Mitral valve dynamics in structural and fluid-structure interaction models [J].Medical Engineering&Physics,2010,32(9): 1057-1064.

[11] Ranganathan N,Lam J H C,Wigle E D,et al.Morphology of the human mitral valve:II.The valve leaflets[J]. Circulation,1970,41:459-467.

[12] Pan F D,Donzella G,Fucci C,et al.Structural effects of an innovative surgical technique to repair heart valve defects[J].J Biomech,2005,38:2460-2471.

[13] Kunzelman K S,Cochran K P.Mechanical properties of basal and marginal mitral valve chordae tendineae[J]. ASAIO Trans,1990,36(3):405-408.

[14] Kunzelman K S,Cochran R P,Murphree S S,et al.Differential collagen distribution in the mitral valve and its influence on biomechanical behaviour[J].J Heart Valve Dis,1993,2:236-244.

[15] 钟琪.人体心脏二尖瓣有限元建模与仿真[D].厦门:厦门大学,2014.

[16] Stevanella M,Votta E,Redaelli A.Mitral valve finite element modeling:implicatioons of tissues′nonlinear response and annular motion[J].Journal of Bionechanical Engineering,2009,131:1-9.

[17] Levick J R.An introduction to cardiovascular physiology [M].London:Hodder Arnold Publication,2003.

[18] 卢晓芳,吕清,谢明星,等.实时三维超声心动图评价二尖瓣裂的初步研究[J].中国医学影像技术,2006,22 (4):490-492.

[19] 钟琪,曾文华,黄晓阳,等.人体二尖瓣建模及生物力学分析[J].医用生物力学,2014,29(1):53-59.

[20] Lansac E,Lim K H,Shomura X,et al.Dynamic balance of the aortomitral junction[J].J Thorac Cardiovasc Surg,2002,123(5):911-918.

[21] Ormiston J A,Shah P M,Tei C,et al.Size and motion of the mitral valve annulus in man.I.A two-dimensional echocardiographic method and findings in normal subjects[J].Circulation,1981,64(1):113-120.

[22] Fyrenius A,Engvall J,Janerot-Sjoberg B.Major and minor axes of the normal mitral annulus[J].J Heart Valve Dis,2001,10(2):146-152.

[23] Gorman III J H,Jackson B M,Enomoto X,et al.The effect of regional ischemia on mitral valve annular saddle shape[J].Ann Thorac Surg,2004,77(2):544-548.

Modeling and Simulation Methods for Mitral Valve Based on the Mitral Valve Sub-region

ZHAO Xiao-jia1,SONG Xiao2,HUANG Xiao-yang1*,SU Mao-long3,ZHONG Qi1
(1.School of Information Science and Engineering,Xiamen University,Xiamen 361005,China;2.College of Computer and Information Technology,Nanyang Normal University,Nanyang 473061,China;3 Ultrasound Department, Zhongshan Hospital,Xiamen University,Xiamen 361004,China)

A fine model of the human mitral valve with non-uniform thickness has been established.The valve closure has been simulated using the finite element method during early systolic period,compared with the uniform one.Simulation results show that the stress is unevenly distributed on the leaflets,that the mitral valve with non-uniform has lower stress level than the uniform one.Furthermore,the maximum principal stresses occurs at the clefts between the three scallops in the posterior leaflet,indicating positions of the mitral valve cleft in clinic. The result is consistent with the physiology.It suggests that the method and the results are correct.Finally,based on clinical data,the motion of annulus and papillary muscles has been simulated,showing higher closure and relatively uniform stress distribution,closer to the actual physiological conditons.It laid the foundation for the simulation of subsequent pathology.

the mitral valve;finite element model;stress distribution;maximum principal stress

10.6043/j.issn.0438-0479.2015.02.021

TP 391

A

0438-0479(2015)02-0276-05

2014-08-28 录用日期:2014-11-19

国家自然科学基金(61102137,61271336,61327001);福建省自然科学基金(2014J01438)

*通信作者:xyhuang@xmu.edu.cn

赵晓佳,宋晓,黄晓阳,等.基于亚区结构的人体二尖瓣的建模与仿真[J].厦门大学学报:自然科学版,2015,54(2): 276-280.

:Zhao Xiaojia,Song Xiao,Huang Xiaoyang,et al.Research on modeling and simulation methods for mitral valve based on the mitral valve sub-region[J].Journal of Xiamen University:Natural Science,2015,54(2):276-280.(in Chinese)