碟式太阳能热发电系统流固耦合模态分析

鄂加强，张庆玲，杨文明，刘腾，王曙辉1, ，王红林，苏秀超，左威



碟式太阳能热发电系统流固耦合模态分析

鄂加强1, 2, 3，张庆玲2，杨文明3，刘腾2，王曙辉1, 2，王红林2，苏秀超2，左威2

(1. 湖南大学汽车车身先进设计制造国家重点实验室，湖南长沙，410082；2. 湖南大学机械与运载工程学院，湖南长沙，410082;3. Department of Mechanical Engineering, National University of Singapore, Singapore 117576, Singapore)

为避免碟式太阳能热发电系统风激共振破坏问题，采用流体控制方程建立碟式太阳能热发电系统流场模型，并将计算得到的碟式太阳能热发电系统流场流速和压力再加载到聚光器前后表面，对碟式太阳能热发电系统流固耦合模态进行分析研究。研究结果表明：流固耦合场对碟式太阳能热发电系统模态振型的影响较小，而对碟式太阳能热发电系统的固有频率和最大变形量的影响较大，但其影响程度随模态阶数的递增而递减；与高度角=0°时碟式太阳能热发电系统固有频率相比，高度角=45°时碟式太阳能热发电系统固有频率均不同程度地减小，但最大变形量基本上保持不变；碟式太阳能热发电系统聚光器的上边缘以及4个悬臂梁靠近电机的部分最容易受到损坏，故应提高此部位的刚度。

碟式太阳能热发电系统；聚光器；流固耦合；模态分析

与化石燃料发电相比，太阳能热发电是降低二氧化碳排放以及减少煤炭资源消耗的一种途径[1−3]。太阳能热发电技术可分为碟式、塔式和槽式共3种类型[4]，其中碟式太阳能热发电系统的太阳能发电效率最高，约占全世界太阳能热发电峰值效率的29.4%，并具有效率最高、结构紧凑、安装方便等特点[5]。为提高碟式太阳能光热发电系统发电效率，人们对聚光器的材料、结构方面进行了许多改进，目前，碟式聚光器已经向单镜面和多镜面张膜式等高效发电技术方向发展[6−8]。考虑碟式太阳能热发电系统一般建设在太阳照射率较高的平地上，受风力作用时会产生巨大载荷，在风载荷作用下可能会产生共振和破坏零件，从而引发安全隐患。自20世纪90年代以来，研究者关于碟式太阳能热发电系统的研究主要集中在提高吸热器能量转化效率[9−12]、聚光器聚光效率[13−15]等方面，而没有针对碟式太阳能热发电系统推广应用的风激振动对碟式太阳能热发电系统模态参数影响机理进行研究。碟式太阳能热发电系统在空气场环境工作时，流动的气体会对太阳能热发电系统的工作性能以及振动特性产生很大影响，同时，在碟式太阳能热发电系统的扰动反过来又会影响到空气场，为典型的流固耦合模型。为此，本文作作者采用简化的物理模型和高精度的数值算法，对碟式太阳能热发电系统流场内部的流速分布和压力分布进行计算，并将计算得到的碟式太阳能热发电系统流场流速和压力再加载到聚光器前后表面，对碟式太阳能热发电系统进行流固耦合计算，确定碟式太阳能热发电系统模态参数，以便为改进碟式太阳能热发电系统结构以及对工程实践中碟式太阳能热发电系统破坏分析提供依据。

1 碟式太阳能聚光器恒定风载作用仿真模型

1.1 守恒方程

由于风载作用于碟式太阳能聚光器是瞬时的不稳定载荷，在分析中不能忽略结构的惯性，必须采用动态分析。为分析问题方便，以下标f表示流体，下标s表示固体。

1.1.1流体控制方程

流体流动要遵循物理守恒定律，基本的守恒定律包括质量守恒定律、动量守恒定律、能量守恒定律。若流体中包含混合的其他成分，则系统还要遵循组分守恒定律。对于一般的可压缩牛顿流来说，守恒定律通过如下控制方程描述。

质量守恒方程：

动量守恒方程：

式中：f为体积力，kg/(m2·s2)；f为剪切力，Pa；为流体压力，Pa；为动力黏度，Pa·s；为单位张量；为速度应力张量，=(+T)/2。

1.1.2 固体控制方程

固体质量守恒方程：

式中：s为固体密度，kg/m3；为柯西应力张量，Pa；s为体积力，kg/(m2·s2)；为固体域当地位移，m。

上述流体和固体控制方程都没有考虑能量方程，若考虑流体、固体的能量传递，需要添加能量方程，对于流体部分的总焓tot能量方程可以写成如下形式：

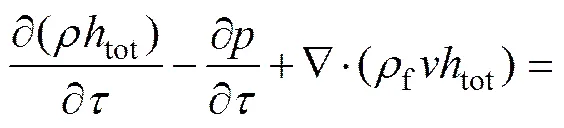
式中：为导热系数，W/(m·K)；E为能量源项，W。

1.1.3 流固耦合方程

在流固耦合的区域，风载荷对碟式太阳能热发电系统的压力可改变碟式太阳能热发电系统的振动模态，而后者反过来又会影响碟式太阳能热发电系统上、下游的气流流速和压力分布。故将计算得到的碟式太阳能热发电系统流场流速和压力再加载到碟式太阳能热发电系统的聚光器前后表面，并对流体控制方程和固体控制方程进行耦合求解。

碟式太阳能热发电系统流固耦合遵循最基本的守恒原则，所以，在流固耦合交接面处，应满足流体应力f与固体应力s、流体位移f和固体位移s、流体热流量f和固体热流量s、流体温度f和固体温度s等变量相等，即满足如下方程：

式中：f为流固耦合交接面处流体法向单位矢量；s为流固耦合交接面处固体法向单位矢量。

1.1.4 模态分析方程

固有频率和振型是系统的固有属性，与外载荷无关。结构的无阻尼自由振动方程为

式中：为结构质量矩阵；为结构刚度矩阵；为节点位移矢量。

对于线性系统，自由振动为简谐形式：

式中：为第(=1, 2, …,)阶固有频率对应的特征向量，即振型向量；ω为第阶固有频率，rad/s。

将式(8)代入式(7)，有

式(9)有非零解(不可能全部为零)的条件为小括号内的行列式必须为0，即特征方程

由式(10)可解得特征值ω2。将ω2代入式(9)，可求得与其对应的特征向量。

1.2 空气与聚光器的有限元网格划分

碟式太阳能发电系统三维模型如图1所示。在图1中，吸热器1是将热能转化为机械能，进而转化为电能的装置；悬臂梁2主要用于支撑斯特林发电机；聚光器3主要用于将入射的太阳辐射能反射到焦点处的斯特林发电机处；支架4的主要作用是支撑聚光器板及其上的悬臂和斯特林发动机，并实现与底座的正确装配；平衡块5主要用于实现与悬臂和发电机的力矩平衡；配重块6主要用于平衡聚光器、吸热器以及支架的重力；底座7主要起支撑和固定的作用。

1—吸热器；2—悬臂梁；3—聚光器；4—支架；5—平衡块；6—配重块；7—底座

碟式太阳能发电系统处于大气边界层中，当风对碟式太阳能发电系统绕流时，相当于碟式太阳能发电系统处于完全开口的流动风场中。风对碟式太阳能发电系统作用的影响在一定的范围内，因此，在数值模拟时需给定一定的三维计算区域且给定与实际中相对应的边界条件。过大的流体区域意味着过大的网格数量，计算量较大，计算时间较长；而若流体区域过小，则流动发展不充分，容易引起计算结果失真，所以，划定合适的流体计算区域对减少计算时间和保证计算精度很重要。碟式太阳能发电系统聚光器直径约为17.00 m，厚度为0.27 m。为保证气流在流体域内的流动达到充分发展的状态，流体域的长度约为聚光器尺寸的10倍，流体域的宽度和高度约为碟式太阳能发电系统聚光器尺寸的5倍。经过多次建模仿真，确定流体域的长×宽×高为170 m×80 m×80 m，模型中心距地面高度为10 m，风的入口距模型中心距离为55 m。碟式太阳能发电系统聚光器的高度角=0°，方位角=0°时的计算域有限元模型如图2所示。

在生成体网格之前，需要根据实际情况进行体网格加密，通过增加网格数量保证计算模型局部位置的计算精度。本计算区域采用逐级加密的划分方式，计算域体网格中间横截面见图3。由图3可以看出分为3个加密区，由远及近逐步加密，保持了一定的连续性，并对聚光器进行单独加密，保证了计算域的体网格质量。网格划分的质量对计算结果的准确性有很大的影响，对该模型的流体区域采用的是多面体网格，非结构网格具有很好的灵活性和适应性，易于进行网格自适应。

1.3 流固耦合场仿真条件

计算域模型流体域的设置需在流固耦合场边界条件设置之前，对于静态稳态分析，物理模型的选择如下：流体域中所选流体为空气；密度取常数1.184 15 kg/m3；湍流模型为标准的K-Epsilon模型；气温为常温且绝热，参考压强为1×105Pa。因在该流体域中流体为低速流动，所以，使用分离求解器，在该流体域内设置初始条件和边界条件。

图2 碟式太阳能热发电系统计算域有限元模型

图3 计算域体网格中间横截面

1) 入口初始条件和边界条件：该区域的流体为不可压缩流体流动，入口初始风速分为恒定风速，风速分别为15，20和25 m/s。

2) 出口边界条件：出口处的边界条件为压力出口，压力设为1×105Pa。

3) 壁面条件：聚光器的外轮廓为圆形，模型半径为8.42 m，最大的正投影面积为222.510 2 m2；流体域底面和聚光器表面的边界条件设为wall，壁面条件的粗糙度设置为光滑。对于黏性流体，采用黏附条件，即认为壁面处流体速度与壁面该处的速度相同，无滑移壁面的速度为0 m/s，壁面处流体速度为0 m/s。聚光器表面和地面是固定不动、不发生移动的，故采用无滑移的壁面条件。而流体域的顶面和前后面采用滑移边界条件。

2 碟式太阳能热发电系统流固耦合模态仿真

2.1 计算频率范围的提取

考虑到高度角一定时碟式太阳能热发电系统可以视为处于无预应力工作状态，因此，碟式太阳能热发电系统的模态分析可以视为无预应力模态分析，即碟式太阳能热发电系统的模态分析结果只与碟式太阳能热发电系统的结构有关(即与碟式太阳能热发电系统的高度角有关，与方位角无关)，故只要针对高度角=0°和高度角=45°时的碟式太阳能热发电系统进行模态分析即可。理论上，具有个自由度的结构系统存在个自振频率及模态振型，但是对碟式太阳能热发电系统的振动起作用的只是低段频率，高阶模态对碟式太阳能热发电系统的振动不会产生大的影响，故本文着重对高度角=0°和=45°时太阳能热发电系统前5阶模态振型进行研究分析。

为揭示流固耦合影响，对碟式太阳能热发电系统前5阶模态振型所对应的固有频率及其最大变形量进行对比分析。

2.2 计算结果与分析

考虑流固耦合影响与未考虑流固耦合影响时，碟式太阳能热发电系统前5阶模态振型基本一致，但前5阶固有频率和最大变形量有明显差别。此外，恒定风速对碟式太阳能热发电系统模态振型也影响甚小。

设考虑流固耦合影响时碟式太阳能热发电系统前5阶模态振型对应的固有频率和最大变形量分别为s和s，未考虑流固耦合影响的碟式太阳能热发电系统前5阶模态振型对应的固有频率和最大变形量分别为c和c，碟式太阳能热发电系统固有频率相对误差和最大变形量相对误差分别为f=(c−s)/s×100%和η=(c−s)/s×100%。

2.2.1高度角=0°时的碟式太阳能热发电系统模态振型

高度角=0°时碟式太阳能热发电系统模态振型如图4所示。由图4可知：碟式太阳能热发电系统1阶模态振型为碟式太阳能热发电系统绕轴的旋转振型，2阶模态振型为碟式太阳能热发电系统绕轴的旋转振型，3阶模态振型为碟式太阳能热发电系统绕轴的旋转振型，4阶模态振型为碟式太阳能热发电系统绕轴的左右偏转振型，5阶模态振型为碟式太阳能热发电系统绕轴的前后偏转振型。

此外，从图4(b)可知：在2阶模态振动过程中，整个碟式太阳能热发电系统的变形量较大，特别是聚光器的上边缘处变形量都达到1.000 mm，容易受到破坏，所以，对碟式太阳能热发电系统的刚度需要提高。从图4(d)可知：在4阶模态振动过程中，3个支撑电机的悬臂梁出现较大变形，靠近电机的部分已达到1.040 mm，容易受到破坏，所以，3个悬臂梁靠近电机的部分的刚度需要提高。

当高度角=0°时，考虑流固耦合影响和未考虑流固耦合影响的碟式太阳能热发电系统固有频率和最大变形量的对比结果如表1所示。从表1可知：是否考虑流固耦合影响对碟式太阳能热发电系统前5阶固有频率的影响程度不一；与考虑流固耦合影响时得到的碟式太阳能热发电系统前5阶固有频率相比，不考虑流固耦合影响时，第2阶、第3阶和第5阶的固有频率增大，分别增大了9.24%，5.21%和3.58%，而第1阶和第4阶的固有频率则减小，分别减小了12.06%和4.76%，但其固有频率的相对误差绝对值随着阶数的增加而递减。这主要是流固耦合场有抑制了碟式太阳能热发电系统固有振型系数的作用，因而流体冲击对较低阶次的碟式太阳能热发电系统固有频率影响较大，而对较高阶次的碟式太阳能热发电系统固有频率影响较小。

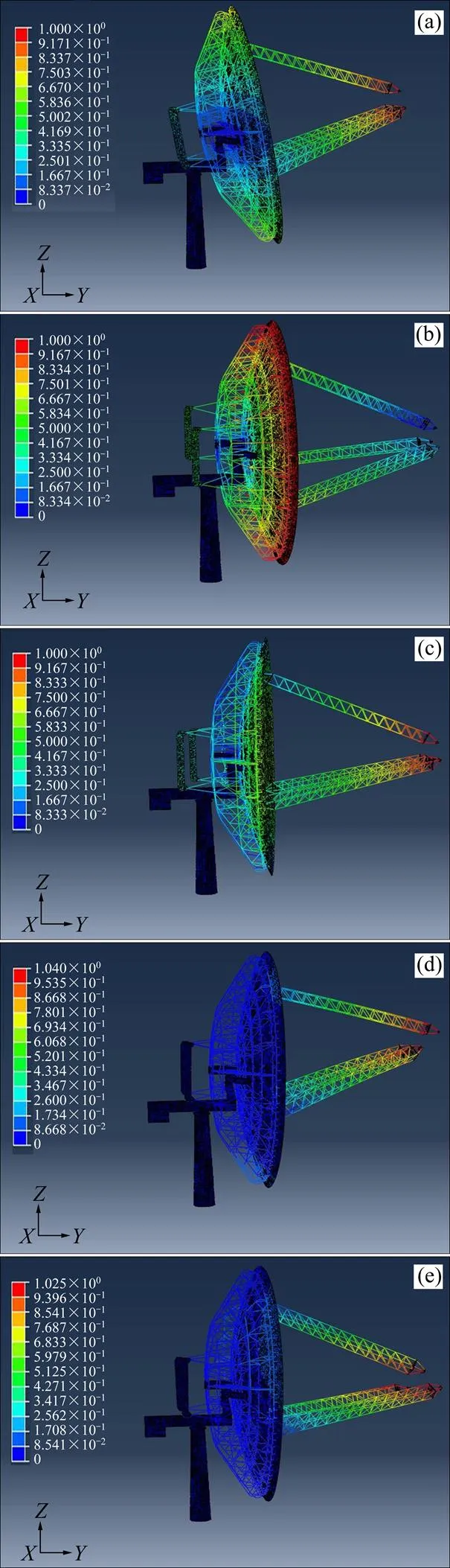
(a) 1阶；(b) 2阶；(c) 3阶；(d) 4阶；(e) 5阶

表1 高度角β=0°时碟式太阳能热发电系统前5阶固有频率和最大变形量对比

与考虑流固耦合影响时得到的碟式太阳能热发电系统前5阶最大变形量相比，不考虑流固耦合影响时碟式太阳能热发电系统前5阶最大变形量的相对误差分别为9.74%，7.81%，6.23%，4.19%和3.65%，可见其最大变形量的相对误差随阶数的递增呈递减的趋势。这主要是因为流体冲击有抑制碟式太阳能热发电系统较高阶次模态变形的作用。流体对较低阶次的碟式太阳能热发电系统最大变形量影响较大，而对较高阶次碟式太阳能热发电系统最大变形量影响较小。

2.2.2高度角=45°时的碟式太阳能热发电系统模态振型

当高度角=45°时碟式太阳能热发电系统模态振型如图5所示。由图5可知：碟式太阳能热发电系统1~5阶模态振型与=0°时的相同。

此外，根据模态分析结果可知：2阶模态时碟式太阳能热发电系统的变形量较大，特别是聚光器的上边缘处变形量都达到1.000 mm，容易受到破坏，所以，聚光器的刚度需要提高；4阶模态时碟式太阳能热发电系统3个支撑电机的悬臂梁出现较大变形，靠近电机的部分已经达到1.043 mm，容易受到破坏，所以，3个悬臂梁靠近电机部分的刚度需要提高。

高度角=45°时考虑流固耦合影响和未考虑流固耦合影响的碟式太阳能热发电系统固有频率和最大变形量的对比结果如表2所示。由表2可知：是否考虑流固耦合影响对碟式太阳能热发电系统前5阶固有频率的影响程度不一；与考虑流固耦合影响时得到的碟式太阳能热发电系统前5阶固有频率相比，不考虑流固耦合影响时，第2阶、第3阶和第5阶的固有频率增大，分别增大了8.54%，6.23%和3.79%，而第1阶和第4阶的固有频率减小，分别减小了10.23%和5.11%，但其固有频率的相对误差绝对值随着阶数的增加而递减。

(a) 1阶；(b) 2阶；(c) 3阶；(d) 4阶；(e) 5阶

与考虑流固耦合影响时得到的碟式太阳能热发电系统前5阶最大变形量相比，不考虑流固耦合影响时碟式太阳能热发电系统前5阶最大变形量的相对误差分别为10.34%，8.56%，7.21%，5.35%和3.78%，可见其最大变形量的相对误差随阶数的递增呈递减 趋势。

与高度角=0°时碟式太阳能热发电系统固有频率相比，高度角=45°时碟式太阳能热发电系统固有频率均相应地不同程度减小，但最大变形量基本上保持不变。这主要是高度角=45°时碟式太阳能热发电系统固有振型系数发生变化所致。

表2 高度角β=45°时碟式太阳能热发电系统前5阶固有频率和最大变形量对比

3 结论

1) 碟式太阳能热发电系统1阶模态振型为碟式太阳能热发电系统绕轴的旋转振型，2阶模态振型为碟式太阳能热发电系统绕轴的旋转振型，3阶模态振型为碟式太阳能热发电系统绕轴旋转振型，4阶模态振型为碟式太阳能热发电系统绕轴的左右偏转振型，5阶模态振型为碟式太阳能热发电系统绕轴前后偏转振型。

2) 考虑流固耦合影响和未考虑流固耦合影响的碟式太阳能热发电系统固有频率和最大变形量的相对误差绝对值均随着阶数的增加而递减，这主要是流固耦合场有抑制碟式太阳能热发电系统较高阶次模态变形的作用，故流体对较低阶次的碟式太阳能热发电系统最大变形量影响较大，而对较高阶次的碟式太阳能热发电系统最大变形量影响较小。

3) 与高度角=0°时碟式太阳能热发电系统固有频率相比，高度角=45°时碟式太阳能热发电系统固有频率均不同程度地减小，但最大变形量基本上保持不变。

4) 对于系统低频段的前5阶固有频率及其相应的振型，聚光器的上边缘以及4个悬臂梁靠近电机的部分最容易受到损坏，故应提高此部位的刚度。

[1] Sardeshpande V R, Chandak A G, Pillai I R. Procedure for thermal performance evaluation of steam generating point-focus solar concentrators[J]. Solar Energy, 2011, 85(7): 1390−1398.

[2] Kaushika N D, Reddy K S. Performance of a low cost solar paraboloidal dish steam generating system[J]. Energy Conversion and Management, 2000, 41(7): 713−726.

[3] Paitoonsurikarn S, Lovegrove K. On the study of convection loss from open cavity receivers in solar paraboloidal dish applications[J]. Destination Renewables, 2003, 26(11): 154−161.

[4] Omer S A, Infield D G. Design and thermal analysis of a two stage solar concentrator for combined heat and thermoelectric power generation[J]. Energy Conversion and Management, 2000, 41(7): 737−756.

[5] Kalogirou S A. Solar thermal collectors and applications[J]. Progress in Energy and Combustion Science, 2004, 30(3): 231−295.

[6] Kumar N S, Reddy K S. Comparison of receivers for solar dish collectors system[J]. Energy Conversion and Management, 2008, 49(4): 812−819.

[7] Christo F C. Numerical modelling of wind and dust patterns around a full-scale paraboloidal solar dish original research article[J]. Renewable Energy, 2012, 39(1): 356−366.

[8] Agneni A, Coppotelli G, Grappasonni C. A method for the harmonic removal in operational modal analysis of rotating blades[J]. Mechanical Systems and Signal Processing, 2012, 27: 604−618.

[9] WU Shuangying, XIAO Lan, CAO Yiding D, et al. Convection heat loss from cavity receiver in parabolic dish solar thermal power system: A review[J]. Solar Energy, 2010, 84(8): 1342−1355.

[10] Reddy K S, Sendhil Kumar N. Combined laminar natural convection and surface radiation heat transfer in a modified cavity receiver of solar parabolic dish[J]. International Journal of Thermal Science, 2008, 47(12): 1647−1657.

[11] Sendhil Kumar N, Reddy K S. Numerical investigation of natural convection heat loss in modified cavity receiver for fuzzy focal solar dish concentrator[J]. Solar Energy, 2007, 81(7): 846−855.

[12] Zanganeh G, Bader R, Pedretti A. A solar dish concentrator based on ellipsoidal polyester membrane facets[J]. Solar Energy, 2012, 86(1): 40−47.

[13] Xiao J, Wei X D, Lu Z W, et al. A review of available methods for surface shape measurement of solar concentrator in solar thermal power applications[J]. Renewable and Sustainable Energy Reviews, 2012, 16(5): 2539−2544.

[14] Hernandez N, Riveros-Rosas D, Venegas E, et al. Conical receiver for a paraboloidal concentrator with large rim angle[J]. Solar Energy, 2012, 86(4): 1053−1062.

[15] Ruelas J, Velázquez N, Cerezo J. A mathematical model to develop a Scheffler-type solar concentrator coupled with a Stirling engine[J]. Applied Energy, 2013, 101(1): 253−260.

(编辑 陈灿华)

Modal analysis on dish solar thermal power system considering fluid-solid interaction

E Jiaqiang1, 2, 3, ZHANG Qingling2, YANG Wenming3, LIU Teng2, WANG Shuhui1, 2, WANG Honglin2, SU Xiuchao2, ZUO Wei2

(1. State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan University, Changsha 410082, China;2. College of Mechanical and Vehicle Engineering, Hunan University, Changsha 410082, China;3. Department of Mechanical Engineering, National University of Singapore, Singapore 117576, Singapore)

In order to avoid resonance destruction problem of dish solar thermal power system caused by wind excitation, the fluid control equations were used to establish the flow field model of dish solar thermal power system. Moreover, the calculated flow velocity and pressure of flow field of the dish solar thermal power system were loaded onto the front and rear surfaces of the condenser, and modal analysis on fluid-structure interaction of dish solar thermal power system was carried out. The results show that the fluid-solid interaction field has little effect on the modal shape of dish solar thermal power system and that the natural frequency and the maximum deformation of dish solar thermal power system are impacted more seriously, although the influence degree shows a decreasing tendency with the increase of mold order. Compared with the natural frequencies of dish solar thermal power system at different azimuth angles when the elevation angle=0°, it has corresponding decrease while the maximum deformations remain essentially unchanged when=45°. The upper edge of the dish solar thermal power system condenser and the portions near the motor of four cantilever beams are most susceptible to be damaged, so the rigidity of these parts should be enhanced properly.

dish solar thermal power system; condenser; fluid-solid interaction; modal analysis

10.11817/j.issn.1672-7207.2015.09.052

TK83

A

1672−7207(2015)09−3546−07

2014−09−15；

2014−11−22

国家留学基金资助项目(201208430262)；武器装备预研重点项目(9140A2011QT4801) (Project(201208430262) supported by the National Fund for Study;Project(9140A2011QT4801) supported by Weapon Research Fund)

鄂加强，博士，博士生导师，从事新能源装备性能仿真与优化等研究；E-mail: ejiaqiang@126.com