公路桥梁基于概率的实用抗震性能设计框架
2015-10-13卓卫东杨宁曾武华
卓卫东,杨宁,曾武华
公路桥梁基于概率的实用抗震性能设计框架
卓卫东,杨宁,曾武华
(福州大学土木工程学院,福建福州,350116)
针对公路桥梁提出实用的基于概率的抗震性能设计框架。在该框架中,针对我国现行规范中同一地震区不同抗震设防类别桥梁遭遇的地震危险性不一致的问题,建议设计基准期统一取为100 a,取超越概率分别为86%,19%,10%和4%的4级设计地震动水平;考虑桥梁震后预期将发挥的使用功能,将其抗震性能水平按正常通行、有限通行、应急通行和禁止通行等功能要求相应地划分为4个等级;抗震性能目标规定为在给定设计地震动水平下结构超过规定的抗震性能水平的条件概率,以期解决我国公路桥梁的抗震设防目标长期没有规定预期的可靠度的问题;采用一次二阶矩法,建立基于需求−能力系数的抗震性能设计的极限状态方程,该方程同时考虑结构地震需求和抗震能力的不确定性。按照本文所提出的设计框架,结合设计算例演示其设计过程。研究结果表明:本文所提出的设计框架可实际应用于公路桥梁基于概率的抗震性能设计。
公路桥梁;抗震性能设计;概率方法;需求−能力系数;框架
自20世纪90年代初美国学者[1]首次提出基于性能的结构抗震设计思想以来,这一新的抗震设计概念得到了国际上的广泛重视与研究。目前,在大部分关于结构抗震性能设计的研究工作中,仅设防地震动水平包含有概率意义,而对结构地震需求和抗震能力的估计则完全是确定性的。然而,结构抗震性能设计中存在大量的不确定性(如地震动、材料强度、几何参数等),因此,基于性能的抗震设计所追求的多级性能目标理应采用概率性描述。Collins等[2]通过引入基于pushover分析的等效单自由度方法和一致危险性反应谱的概念,提出把可靠度理论与基于性能的抗震设计理论相结合的设计方法,考虑了地震危险性、场地类别效应及结构模型简化存在的不确定。Bertero等[3]认为结构地震需求的不确定性远大于结构抗震能力的不确定性,建议忽略结构抗震能力的不确定性,在目标可靠度确定前提下,采用荷载分项系数的形式来考虑结构地震需求的不确定性。Cornell等[4]提出需求−能力系数设计方法,以考虑钢框架结构抗震分析时地震动危险性水平、结构非线性位移需求和位移能力中存在的不确定性,该方法类似于常规的荷载−抗力分项系数设计方法,已被美国联邦应急管理署颁发的设计准则(FEMA 350)所采用。Deierlein等[5−7]提出了新一代的基于概率和性能的地震工程框架,该框架建立在全概率理论基础上,将性能评估的全过程分为相对独立又具有逻辑联系的4个阶段:地震危险性分析、结构反应分析、损伤分析及损失评估。Mackie等[8]基于Deierlein等[5−7]提出的框架,针对桥梁结构给出了基于概率的抗震性能设计方法,其设计准则以连续的极限状态形式规定,并且明确考虑地震危险性以及结构需求、损伤和损失的不确定。张海燕等[9]结合概率延性需求谱和可靠度分析的验算点法,提出了基于位移的目标可靠指标直接进行结构设计的方法。吕大刚等[10]采用可靠度的全概率数值模拟计算方法,实现钢框架结构构件和结构体系2个层次上的基于变形可靠度的全概率设计。Zacharenaki等[11]在优化算法的框架下,采用简化的增量动力分析方法,快速计算极限状态的年平均超越概率,进而提出了基于可靠度的结构抗震设计优化方法。对于桥梁结构常规的静力设计,各国现行规范已普遍采用荷载−抗力分项系数设计方法,以考虑荷载和抗力的不确定性;然而对于桥梁结构的抗震性能设计,基于概率的设计方法研究才刚刚起步。本文作者针对公路桥梁,提出基于概率的实用抗震性能设计框架,在该框架中,采用4级设计地震动水平与4级抗震性能水平组合形成基于可靠度的抗震性能目标矩阵,结构抗震性能目标可靠度通过基于需求−能力系数的极限状态方程来体现,并在其中同时考虑结构地震需求和抗震能力的不确定性。本文作者所提出的设计框架,可实际应用于公路桥梁基于概率的抗震性能设计。
1 基于可靠度的抗震性能目标
1.1 设计地震动水平
由于地震发生的时间、空间分布均具有极大的不确定性,各个地方、各个时期可能发生的地震震级大小也是不确定的,因此,应当在概率的基础上进行地震危险性分析。特定场地的地震危险性常采用设计基准期内超越概率或重现期来表示,而地震重现期、设计基准期和超越概率之间的关系为[12]
式中:R为重现期;0为规定的设计基准期;P0(M)为设计基准期内地震动强度超过某给定值M的超越概率。
通过概率地震危险性分析得到的地震危险性曲线能够完整地描述场地的地震危险性,然而为了便于工程应用,在结构抗震设计规范中,往往采用离散的设计地震动水平进行抗震设防。对于公路桥梁,我国1989年颁发的JTJ 004—89“公路工程抗震设计规 范”[13]采用重现期为475 a的单一设防地震动水平,显然,采用单一设防水准的设计思想,不能保证桥梁的抗震性能得到有效的控制;在我国现行JTG/T B02-01—2008“公路桥梁抗震设计细则”[14]中,采用了E1和E2这2级设计地震动水平:其中,E1地震对A类桥重现期为475 a,对B和C类桥重现期为50~100 a,对D类桥重现期为25 a;E2地震对A类桥重现期为2 000 a,B和C类桥重现期为475~ 2 000 a。现行规范将公路桥梁的抗震设防类别划分为4类,并针对不同类别的桥梁,采用重要性系数直接调整其设计地震动参数,这种做法忽视同一地震区地震危险性的一致性,造成人为地夸大或缩小了桥梁所面临的地震危险性。
在现行规范颁发之前,我国对特大跨径的公路桥梁(单跨跨径在150 m以上)没有规定其设计地震动水平,国内的习惯做法是直接采用地震安全性评价给出的建议设防地震动水平。表1所示为国内部分已建的大型桥梁工程所采用的设计地震动水平。从表1可见:大型桥梁工程普遍采用了2级设计地震动水平,然而不同工程采用的地震动重现期没有一个统一的标准。现行规范虽然规定了特大跨径桥梁的设计地震动水平,然而依旧采用了2级设计地震动水平。
从基于概率和性能的设计角度出发,针对不同抗震设防类别的桥梁采用统一的设计地震动水平,对不同类别的桥梁规定不同的抗震性能目标可靠度,以体现其抗震设防目标的差异,应是一种比现行规范更为合理的做法。显然,为了实现基于性能的抗震设计的多个性能目标,设计地震动水平也必须是多级的。基于这种思路,本文参考目前相关的主要研究成 果[15−16],建议对公路桥梁采用表2所示的统一的4级设防地震动水平。本文所建议的设防地震动水平,设计基准期统一取为100 a,与现行JTG D60—2004 “公路桥涵设计通用规范”[17]的相关规定一致;4级设防地震动水平对应的超越概率分别为86%,19%,10%和4%,对应的重现期分别为50,475,950和 2 450 a,其最大和最小地震发生概率基本与现行规范规定的2级设计地震动水平相当。
1.2 桥梁抗震性能水平
桥梁的抗震性能水平是指桥梁遭遇地震作用时限定的结构损伤状态。在基于性能的抗震设计思想提出后,在美国加州结构工程师协会(SEAOC)Vision 2000[1]中提出将建筑结构的抗震性能水平划分为4个等级,依次为正常使用、修复使用、生命安全和防止倒塌。与普通建筑不同,桥梁是陆路交通系统的枢纽工程,国际上称之为抗震救灾的生命线工程。在1995年日本阪神地震中,因桥梁严重破坏造成公路中断,交通系统处处受阻,全线处于“死亡”状态,造成了极为惨重的经济损失;在2008年汶川地震中,因桥梁坍塌或严重破坏造成通往重灾区的公路交通全部中断,严重影响了抗震救灾和灾后重建工作,社会影响巨大。随着我国社会经济持续发展和大量人口向现代化中心城市聚集,对交通网络的依赖程度将越来越高,一旦桥梁遭受地震严重破坏,可能导致的间接经济损失将会越来越大。因此,对于公路桥梁而言,在规定其抗震性能水平时,应充分考虑其在地震后预期将发挥的使用功能。根据地震后不同的功能要求:正常通行、有限通行、应急通行和禁止通行,本文将公路桥梁的抗震性能水平相应地划分为4个等级,如表3所示。
尽管对公路桥梁可以给出表3所示的各抗震性能水平的明确定义和定性的功能描述,然而,要实现基于性能的抗震设计,还需要针对结构构件给出量化的性能指标。本文作者前期的研究[18]表明:公路规则桥梁的抗震性能水平可以采用桥墩的抗震性能水平来定义,并且可以用墩顶侧移率作为性能设计参数,对其抗震性能水平予以定量化的描述。墩顶侧移率定义为墩顶地震位移反应与墩高之比。本文作者进一步研究各极限状态(即达到限定的结构损伤状态)下墩顶侧移率的概率特征。结果表明:当规则桥梁达到各限定的结构损伤状态时,桥墩可达到的相应的墩顶侧移率服从对数正态分布,其概率特征值如表4所示。
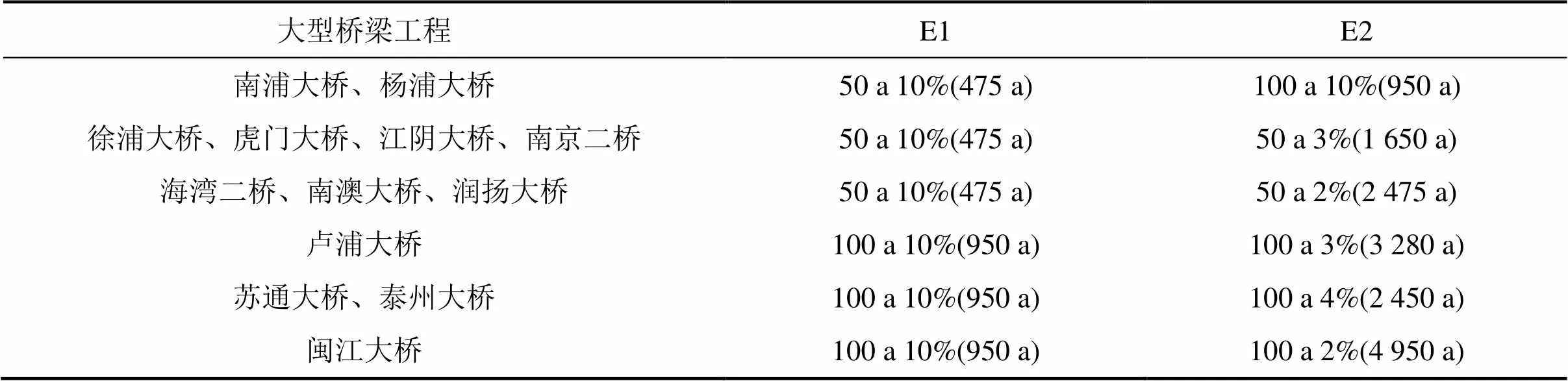
表1 部分大型桥梁工程的设计地震动水平
注:50 a 10%(475 a)表示50 a内超越概率为10%(地震动重现周期为475 a)。

表2 建议的设计地震动水平

表3 建议的公路桥梁抗震性能水平
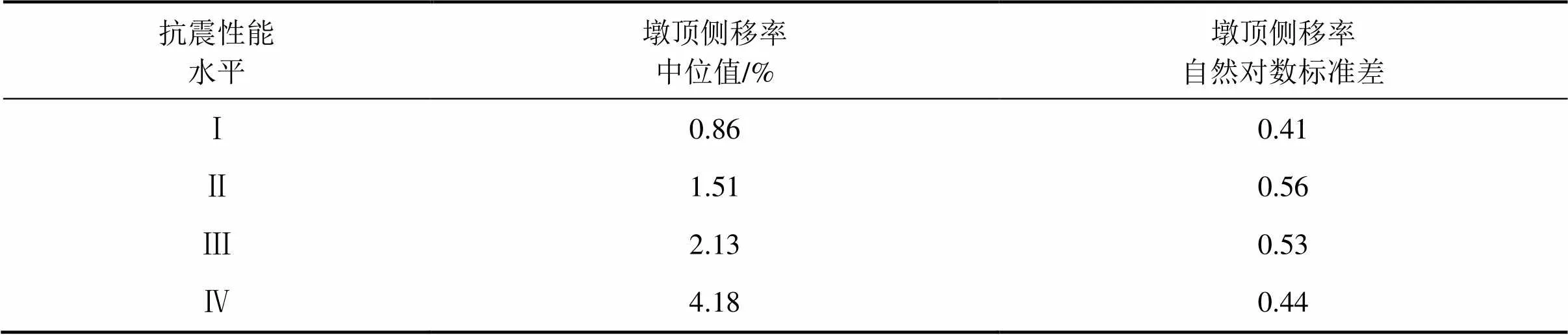
表4 各极限状态下墩顶侧移率的概率特征值
1.3 基于可靠度的桥梁抗震性能目标矩阵
桥梁抗震性能目标矩阵是指在规定的各级设计地震动水平下桥梁结构预期达到的相应抗震性能水平的总和。它是基于性能的桥梁抗震设计要求达到的总目标,也是衡量桥梁抗震性能设计水平的一个尺度。为了使基于性能的抗震设计所追求的多级性能目标有保障,本文建议采用图1所示的基于可靠度的抗震性能目标矩阵。图1中:为目标可靠指标。图1所示的基于可靠度的抗震性能目标矩阵,实际是对传统的“小震不坏、中震可修、大震不倒”原则的进一步细化,并规定了达到各级抗震性能目标应该满足的预期可靠度。目标可靠度的确定是可靠度设计的起始点,然而,确定桥梁抗震性能目标的可靠度水平是一个很复杂的问题,最理想的做法是通过全寿命周期成本优化法来确定,但是要应用于实际抗震设计中操作较困难。参考马宏旺[19]的研究,本文作者针对现行规范规定的4类不同抗震设防类别的桥梁,提出了表5所示的抗震性能目标可靠度的参考取值。从表5可以看出:4类不同抗震设防类别的桥梁在遭遇E1地震作用时,对应“正常通行”的目标可靠指标取值范围为0.6~1.5,基本与我国GB/T 50283—1999“公路工程结构可靠度设计统一标准”[20]中建议正常使用极限状态设计的目标可靠指标控制值相当。另外,根据基于性能的抗震设计的个性化特点,抗震性能目标的可靠度可以通过设计人员和业主之间协商确定,在全面考虑桥梁的安全、性能、经济和社会等多方面影响情况下,业主可根据自己的经济实力在经济与性能之间选择合理的可靠度。
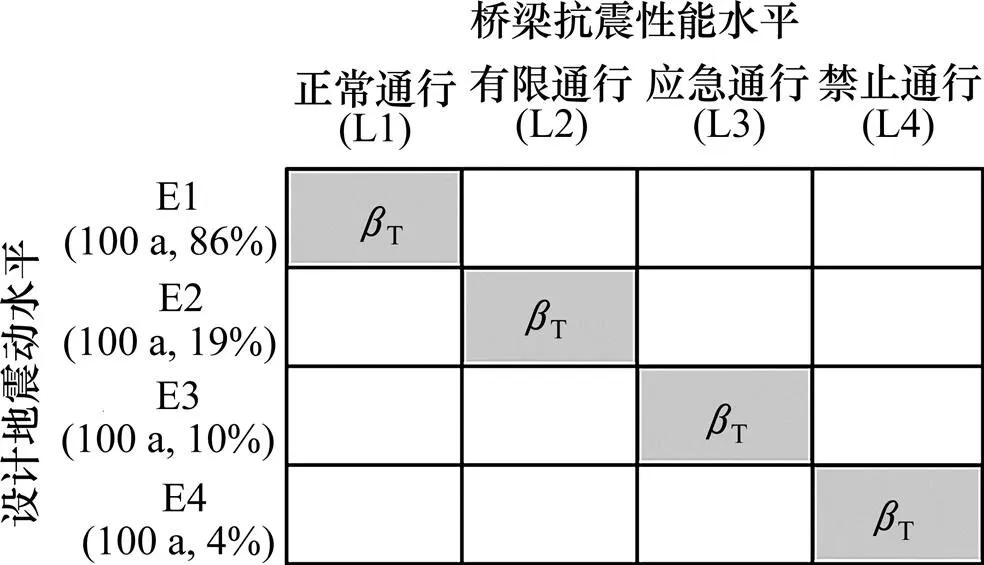
图1 公路桥梁基于可靠度的抗震性能目标矩阵

表5 公路桥梁抗震性能设计目标可靠度建议取值
2 基于概率的抗震性能设计框架
根据基于概率和性能的抗震设计的基本思想,提出基于概率的桥梁抗震性能设计流程,如图2所示。在该设计流程中,要点是结构地震需求和抗震能力计算都是基于概率方法,而且采用概率设计方法来平衡结构地震需求和抗震能力,使得基于性能的抗震设计所追求的抗震性能目标具有概率意义上的保证。
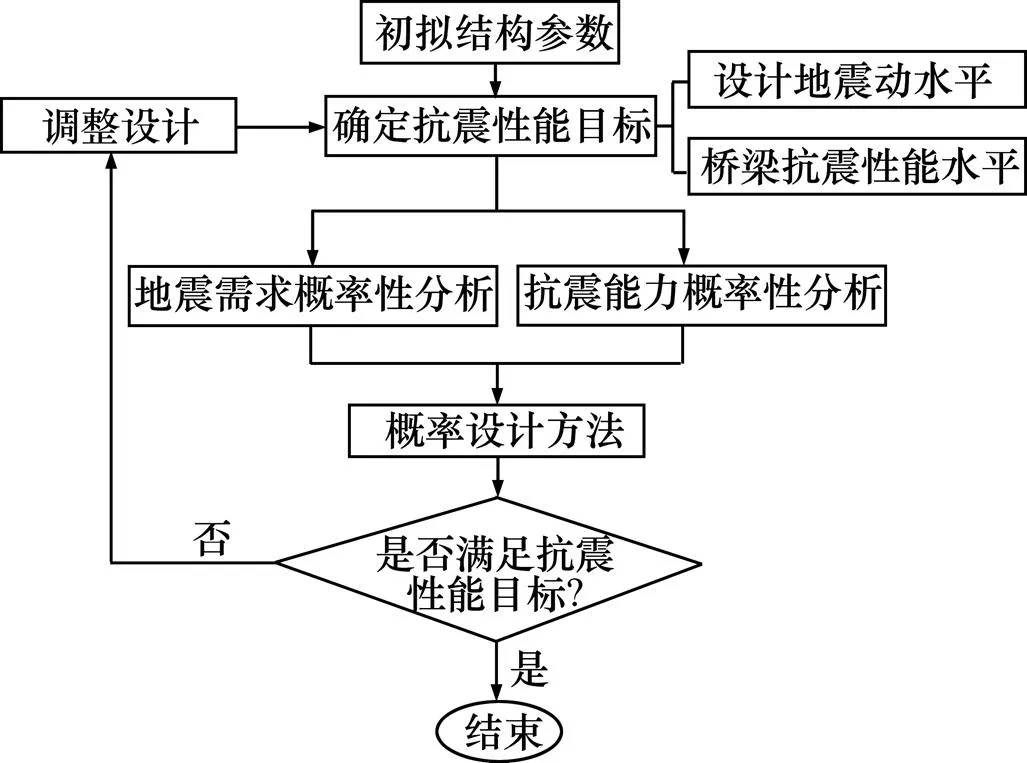
图2 公路桥梁基于概率的抗震性能设计流程
为了简化概率设计过程,采用墩顶侧移率作为性能设计参数,并采用以下的假定:
1) 同时考虑永久作用、可变作用和地震作用,假定这三者的最不利效应组合,即偶然组合控制结构设计。
2) 假定偶然组合(即结构地震需求)仅考虑地震作用效应,忽略永久作用和可变作用的效应。这个假定在采用墩顶侧移率作为性能设计参数时是合理的。
3) 假定结构需求和能力均服从对数正态分布。
定义如下功能函数:
式中:和分别为结构概率抗震能力和概率地震 需求。
根据以上假定,功能函数服从正态分布。采用一次二阶矩法[21],其失效概率可表示为
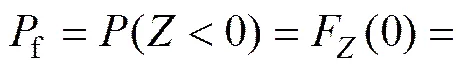
(3)
式中的可靠指标采用下式计算:
式中:m和分别为结构需求中位值和自然对数标准差;m和分别为能力中位值和自然对数标准差。
对式(4)采用分离系数法,可得到结构可靠指标大于或等于给定的目标可靠指标时结构地震需求、抗震能力分项系数的极限状态方程,其形式如下:
式(5)所示的桥梁抗震性能设计的极限状态方程,通过结构地震需求和抗震能力2个分项系数,同时考虑了结构需求和能力的不确定性。通过规定合理的目标可靠指标,就可保证桥梁满足预期的抗震性能目标可靠度。
理论研究表明,当失效概率f≥10−3时,采用一次二阶矩法估算失效概率,可以不考虑功能函数实际的分布类型[21]。因此,本文假定公路桥梁的结构需求和能力均服从对数正态分布,不仅具有合理性,而且便于建立其抗震性能设计的极限状态方程。
3 设计算例
某二级公路上1座4跨一联钢筋混凝土公路连续梁桥,桥跨组合为4×18 m(孔数×跨径),除了在其中的1中墩上设置固定支座外,其余墩(台)均为活动支座,如图3所示。上部结构采用等截面单箱单室箱梁,结构重力为110 kN/m。下部结构采用圆形截面独柱式桥墩,墩高为10 m,初拟墩身直径取为1.8 m,混凝土等级为C30,纵筋采用38根直径为32 mm的HRB400钢筋,箍筋选用直径为12 mm的HRB335级钢筋,如图4所示。该桥址位于Ⅲ类场地,场地特征周期为0.55 s,地震危险性性特征分区为Ⅱ区,抗震设防烈度为8度。
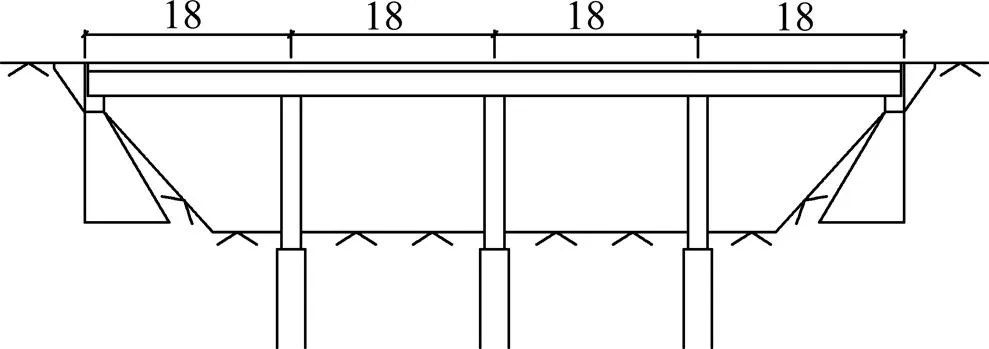
单位:m
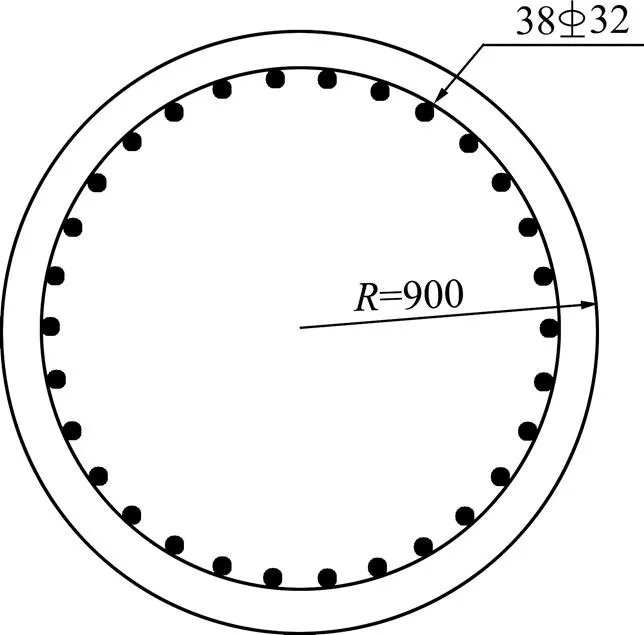
单位:mm
采用本文建立的理论框架对该桥进行基于概率和性能的抗震设计,具体设计过程如下:
1) 确定桥梁抗震性能目标:假设该桥属于C类桥,则根据表5和图1所示的桥梁抗震性能目标矩阵,该桥的目标可靠指标T为0.9,其抗震性能目标为:E1地震作用下正常通行、E2地震作用下有限通行、E3地震作用下应急通行、E4地震作用下禁止通行的保证率均为82%;
2) 各设计地震动水平下的结构地震需求概率性分析:根据谢礼立等[22]的研究成果,可以确定本文所建议的4级设计地震动水平相应的地震动参数取值,如表6所示。根据作者的研究结果[23],对规则桥梁,采用墩顶侧移率作为性能设计参数时,结构需求中位值m可以采用下式计算,且自然对数标准差为0.6:
式中:为规则桥梁的自振基本周期;a为阻尼比5%时,与结构基本周期对应的谱加速度。
经计算,该桥纵桥向的自振基本周期为0.75 s;代入式(8),计算得到了各设计地震动水平下的结构需求中位值m,算例桥梁计算参数如表7所示。
3) 与各抗震性能水平对应的结构抗震能力概率性分析:具体结果如表4所示。

表6 各级设计地震动水平下地震动参数值
4) 需求−能力系数计算:分别将T,和代入式(6)和式(7)中,计算得到需求分项系数和能力分项系数,计算结果如表7所示。
5) 验算抗震性能目标:根据式(5),验算该桥的抗震性能目标是否满足。从表7可以看出:该桥在4级设防地震作用下,结构需求设计值均小于或等于能力设计值,表明该桥能够满足预期的各级抗震性能目标。
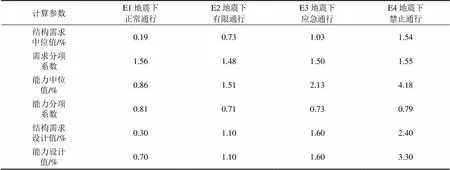
表7 算例桥梁计算参数
以上设计算例仅针对纵向地震作用进行设计分析,横向地震作用下的设计分析过程与纵向地震作用设计分析完全相同。该算例仅针对规则桥梁,对复杂桥梁如曲线、斜交梁桥或特殊桥梁如斜拉桥、悬索桥等,有必要研究其结构概率地震需求和概率抗震能力,以实现这类桥梁基于概率的抗震性能设计。
4 结论
1) 建议对公路桥梁统一采用100 a设计基准期,取超越概率分别为86%,19%,10%和4%的4级设计地震动水平,对应的重现周期分别为50,475,950和2 450 a。所建议的最小和最大设计地震动水平基本与现行规范规定的2级设计地震动水平相当。
2) 提出按正常通行、有限通行、应急通行和禁止通行等震后预期将发挥的使用功能要求,将公路桥梁的抗震性能水平划分为相应的4个等级。
3) 提出基于可靠度的桥梁抗震性能目标矩阵,针对现行规范规定的4类不同抗震设防类别的桥梁,建议了其目标可靠指标和失效概率。
4) 提出公路桥梁基于概率的抗震性能设计流程和采用结构地震需求−抗震能力系数的概率设计框架,所提出的设计框架可实际应用于公路桥梁基于概率的抗震性能设计。
[1] SEAOC Vision 2000. Performance based seismic engineering of buildings[R]. Sacramento, California, USA: Structural Engineers Association of California, 1995: 1-1−2-10.
[2] Collins K R, Wen Y K, Foutch D A. Dual-level seismic design: A reliability-based method[J]. Earthquake Engineering & Structural Dynamics, 1996, 25(12): 1433−1467.
[3] Bertero R D, Bertero V V. Performance-based seismic engineering: The need for a reliable conceptual comprehensive approach[J]. Earthquake Engineering and Structural Dynamics, 2002, 31(3): 627−652.
[4] Cornell C A, Jalayer F, Hamburger R O, et al. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines[J]. Journal of Structural Engineering, 2002, 128(4): 526−533.
[5] Deierlein G G, Krawinkler H, Cornell C A. A Framework for performance-Based earthquake engineering[C]// Proceedings of 2003 Pacific Conference on Earthquake Engineering. Christchurch , New Zealand: CD-ROOM, Elsevier, 2003: 1−8.
[6] Porter K A. An Overview of PEER’s performance-Based earthquake engineering methodology[C]// Proceedings of Ninth International Conference on Applications of Statistics and Probability in Civil Engineering. San Francisco, California: CD-ROOM, Elsevier, 2003: 1−8.
[7] Moehle J, Deierlein G G. A Framework methodology for performance-Based engineering[C]// Proceedings of 13th World Conference on Earthquake Engineering. Vancouver B C, Canada: CD-ROOM, Elsevier, 2004: 1−6.
[8] Mackie K R, Stojadinovic B. Performance-based seismic bridge design for damage and loss limit states[J]. Earthquake Engineering and Structural Dynamics, 2007, 36(13): 1953−1971.
[9] 张海燕, 易伟建. 基于位移的概率极限状态设计[J]. 地震工程与工程振动, 2009, 29(1): 83−89. ZHANG Haiyan, YI Weijian. Displacement-based probabilistic limit state design[J]. Journal of Earthquake Engineering and Engineering Vibration 2009, 29(1): 83−89.
[10] 吕大刚, 贾明明. 钢框架结构基于变形可靠度的全概率抗震设计[J]. 工程力学, 2011, 28(5): 117−223. LÜ Dagang, JIA Mingming. Full probability aseismic design of steel frame structures based on deformation reliability[J]. Engineering Mechanics, 2011, 28(5): 117−223.
[11] Zacharenaki A E, Fragiadakis M, Papadrakakis M. Reliability- based optimum seismic design of structures using simplified performance estimation methods[J]. Engineering Structures, 2013, 52(3): 707−717.
[12] 胡聿贤. 地震工程学[M]. 2版. 北京: 地震出版社, 2006: 361−380. HU Yuxian. Earthquake engineering[M]. 2nd ed. Beijing: Earthquake Press, 2006: 361−380.
[13] JTJ 004—89, 公路工程抗震设计规范[S]. JTJ 004—89, Anti-seismic design code for highway engineering[S].
[14] TG/T B02-01—2008, 公路桥梁抗震设计细则[S]. TG/TB02-01—2008, Guidelines for seismic design of highway bridges[S].
[15] FEMA 273. NEHRP guidelines for the seismic rehabilitation of buildings[R]. Washington, DC, USA: Federal Emergency Management Agency, 1997: 1-1−2-50.
[16] ATC-40. Seismic evaluation and retrofit of concrete buildings [R]. Redwood City, California, USA: Applied Technology Council, 1996: 1-1−4-12.
[17] JTG D60—2004, 公路桥涵设计通用规范[S]. JTG D60—2004, General code for design of highway bridges and culverts[S].
[18] 孙颖, 卓卫东, 房贞政. 规则桥梁抗震性能水准的定义及其量化描述[J]. 地震工程与工程振动, 2011, 31(5): 104−112. SUN Ying, ZHUO Weidong, FANG Zhenzheng. Definition and quantified description of seismic performance levels for regular bridges[J]. Journal of Earthquake Engineering and Engineering Vibration, 2011, 31(5): 104−112.
[19] 马宏旺. 钢筋混凝土框架结构抗震可靠度分析与设计研究[D]. 大连: 大连理工大学土木工程学院, 2001: 103−104. MA Hongwang. Seismic reliability analysis and design of reinforced concrete frames[D]. Dalian: Dalian University of Technology. School of Civil Engineering, 2001: 103−104.
[20] GB/T 50283—1999, 公路工程结构可靠度设计统一标准[S].GB/T 50283—1999, Unified standard for reliability design of highway engineering structures[S].
[21] 赵国藩, 曹居易, 张宽权. 工程结构可靠度[M]. 北京: 科学出版社, 2011: 25−75. ZHAO Guofan, CAO Juyi, ZHANG Kuquan. Engineering structure reliability[M]. Beijing: Science Press, 2011: 25−75.
[22] 谢礼立, 马玉宏, 翟长海. 基于性态的抗震设防与设计地震动[M]. 北京: 科学出版社, 2009: 221−242. XIE Lili, MA Yuhong, ZHAI Changhai, Performance-based seismic design and design ground motion[M]. Beijing: Science Press. 2009: 221−242.
[23] 卓卫东, 曾武华. 公路规则桥梁实用概率地震需求模型[J]. 地震工程与工程振动, 2014, 34(2): 64−70.ZHUO Weidong, ZENG Wuhua. A practical probabilistic seismic demand model for regular bridges[J]. Journal of Earthquake Engineering and Engineering Vibration, 2014, 34(2): 64−70.
(编辑 罗金花)
A practical framework for probability and performance-based seismic design of highway bridges
ZHUO Weidong, YANG Ning, ZENG Wuhua
(College of Civil Engineering, Fuzhou University, Fuzhou 350116, China)
A practical framework of seismic design based on probability and performance for highway bridges was proposed. In the framework, four earthquake design levels were recommended in terms of the exceeding probability of 86%, 19%, 10% and 4% in 100 years, to solve the inconsistency of seismic hazard for highway bridges with different seismic fortification classification at the same earthquake zone in current Chinese guidelines for seismic design of highway bridges. Four seismic performance levels were proposed, i.e. immediately operational, limited operational, emergency traffic only, and closed to traffic, respectively, according to the expected functional requirements of highway bridges after an earthquake shock. The seismic performance objective was defined as the conditional probability of exceeding a specified performance level at the given earthquake design level, to solve the problem that the reliabilities of seismic fortification goals of highway bridges had not been specified. The first order second moment method was used to derive the limit state equation of seismic design based on performance for highway bridges, in which both demand and capacity factors were used to explain the uncertainty in the seismic demand and capacity. On the basis of the proposed framework, the design procedure was demonstrated by an example highway girder bridge. The results show that the proposed framework can be practically applied to seismic design based on probability and performance for highway bridges.
highway bridge; performance-based seismic design; probabilistic method; demand−capacity factors; framework
10.11817/j.issn.1672-7207.2015.09.041
U422.55
A
1672−7207(2015)09−3468−07
2014−12−06;
2015−02−06
高等学校博士学科点专项科研基金资助项目(20113514110003) (Project(20113514110003) supported by the Specialized Research Fund for the Doctoral Program of Higher Education)
卓卫东,博士,教授,博士生导师,从事桥梁抗震研究;E-mail: zhuowd@fzu.edu.cn
