基于土体非线性性质的土−堆石坝动力相互作用(SRDI)体系的动力特性
2015-10-13夏栋舟刘瀛之刘建华
夏栋舟,刘瀛之,刘建华
基于土体非线性性质的土−堆石坝动力相互作用(SRDI)体系的动力特性
夏栋舟1,刘瀛之1,刘建华2
(1. 长沙理工大学土木与建筑学院,湖南长沙,410114;2. 长沙理工大学交通运输工程学院,湖南长沙, 410114)
运用Davidenkov地基模型,选取合理的模型参数实现对土体非线性性质的有限元模拟,并考虑土体边界条件、土体与坝体间接触界面状态非线性、地基土辐射阻尼以及坝体与土体耦合阻尼比等因素,对土−堆石坝动力相互作用(SRDI)体系动力特性进行ANSYS有限元模拟与分析。研究结果表明:软土地基对地震作用的放大效应会导致土体加速度和位移幅值随深度减小而变大,土与坝体的材料阻尼以及土与坝体接触界面间的阻尼效应减小坝体的动力反应,改善土−堆石坝体系的整体抗震性能,可为堆石坝工程的设计与实践提供参考。
非线性;土−堆石坝动力相互作用;辐射阻尼;抗震性能
自改革开放以来,我国在水力资源丰富的西南、西北地区兴建了很多大型水利水电工程。这些地区处于地中海喜玛拉雅地震带,是我国地震活动最活跃的地区之一[1],其设计地震烈度都高达Ⅷ度或Ⅸ度。同时,根据国家对水利水电建设的政策要求,民营资本也可以参与各类小水电站的建设,这些水电站的蓄水坝体安全性能关系到能源的供给以及人身安全,因此,对各类蓄水坝体的抗震设计以及地震安全性能进行评估,对确保坝体安全性能具有重要的现实意义。在小水电站建设中,应用较广泛的是堆石坝体系,而目前人们对考虑地基土和堆石坝体系动力相互作用的研 究[2−9]较少,其主要原因是有多个关键问题一直未得到有效解决,如在有限元动力分析与模拟计算中,尚未解决土体非线性以及地基土与坝体共同作用的问题,其难点主要体现在:土体非线性特性在有限元研究方法中的模拟;土体边界条件的考虑及在有限元方法中的实现;土体与坝体间接触界面状态非线性的模拟;地基土辐射阻尼的模拟;坝体与土体耦合阻尼比的研究等。为此,本文作者利用有限元方法实现非线性土体与堆石坝动力相互作用的模拟,并考察土体与坝体各关键位置的动力特性,以便为工程设计与实践提供参考。
1 地基土非线性动力本构模型的建立
已有研究成果[10]表明:运用Davidenkov地基模型,选取合理的模型参数,通过ANSYS重新启动分析方法可以实现对土体材料的非线性模拟。
本文采用Martin[11]提出的Davidenkov模型描述各类土剪应力与剪应变之间的关系。其动剪切模量d与最大动剪切模量max比值与土的动剪应变的关系式为(其中,)。对于土的滞回曲线−,根据有关试验结果,可以用如下经验公式表示:(其中,为土的阻尼比;为最大阻尼比;为土的参考剪应变;为−曲线的形状系数,对于大多数土,的取值为0.2~1.2)。
Davidenkov模型参数最大动剪切模量的选取可使用以下2种方法。
1) 经验公式法。采用Hardin等[12]提出的适用于各类土的经验公式:。其中:为与不同土类相关的常数;为不同土类的孔隙比;为不同土类的平均有效围压;OC为不同土类的超固结比;为与土的塑性指数p有关的参数。
Davidenkov模型参数动阻尼比据孙静[13]对国内不同地区的土样采用共振柱试验方法所得的试验结果选取。
2 动力分析方法及关键问题的解决
2.1 土−堆石坝时域分析方法
与静力学问题的有限元法一样,动力学问题的有限元法要将物体离散为数量有限的单元体,同时,物体所受的载荷还要考虑单元的惯性力和阻尼力等因素。为了提高计算精度和稳定性并降低计算费用,可运用逐步积分的基本思想,在每个时间间隔Δ内,将位移、速度和加速度都假设遵循某种变化规律,从而引出各种算法。常用的直接积分方法有中心差分法、Wilson-θ法、Newmark法等。本文采用Newmark算法进行时域分析,其原理见文献[14]。本文中Newmark算法的解题步骤如下。
1) 初始值的计算。
① 确定刚度矩阵、质量矩阵和阻尼矩阵。

;;;;


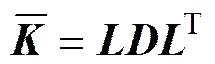
2) 相关参数的计算。

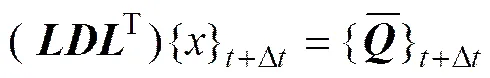

采用完全法,运用完整的系统矩阵计算各种类型的非线性(如接触单元、塑性、蠕变等)瞬态响应,并且可以在1次处理过程中计算所有的位移和应力。
2.2 边界问题的处理
用有限单元法分析土−堆石坝动力相互作用时,需从半无限的地球介质中切取出感兴趣的有限计算区。土体辐射阻尼效应导致地震能量不再单纯地由地基土及坝体本身材料阻尼所消耗,因此,在切取的边界上需建立人工边界以模拟辐射阻尼效应,保证由坝体产生的散射波从有限计算区内部穿过人工边界而不发生反射。本文计算时采用黏弹性边界,通过设置由线性弹簧和黏性阻尼器组合而成的力学模型来吸收射向人工边界的波动能量,从而达到以有限介质代替无限介质的目的。在ANSYS中,用Combin14模拟黏弹性边界。
2.3 阻尼问题的处理
在动力荷载作用下,材料阻尼有2种:1) 几何阻尼。动力荷载以弹性波的方式在材料内传播时,因波面的增大而导致能量损失;2) 材料内阻尼。由于材料内部的摩擦及黏性效应所产生的能量损失。ANSYS程序中可以定义5种形式的阻尼:Rayleigh阻尼、与材料相关的阻尼、恒定阻尼比、振型阻尼和单元阻尼。通常可以在模型中定义多种形式的阻尼,在ANSYS程序中按定义的阻尼之和形成耦合阻尼矩阵[]。其通用形式为

(1)
在土−堆石坝动力相互作用问题中,地基土与坝体材料不同导致土−堆石坝动力相互作用体系的阻尼往往大于坝体本身的阻尼。对于坝体和地基应该采用不同的和,在这种情况下,不同的振型对于阻尼矩阵[]不再是正交的,以致不同振型之间不能解耦,需采用Newmark时域分析法求解。
采用上述与材料相关阻尼的输入方法,分别输入土体和坝体各自材料的阻尼,按式(1)集成阻尼矩阵。材料刚度矩阵常系数与Rayleigh阻尼中忽略Alphad阻尼情况下Beta阻尼求法的相同,
2.4 土体与坝体接触界面上的状态非线性模拟
由于堆石、混凝土材料与土这种材料性质相差很远的介质界面,仅在一定应力水平范围内才能保持位移的连续性,所以,传统动力学分析中,接触面的处理大多采用2种材料的变形完全协调的假定不适用。在分析土与坝体接触界面上的状态非线性问题时主要采用以下3种方法:
1) 非线性S-R模型。取弹簧刚度与阻尼表达式中的土剪切模量为有效接触比的函数,近似考虑土体的非线性。此方法简单、方便,对于定性分析具有一定的价值。
2) 离散单元法。根据代表单个物体的离散元的每一集合来建立动力平衡方程,并通过接触监测算法自动监视各物体间的相互作用。
3) 有限元法。在坝体−地基体系有限元模型中的坝体−地基交界面处,加设具有可模拟滑移、脱开和重新闭合的非线性特性界面单元,代表性的有Goodman单元、薄层单元、薄层的土单元。
本文据文献[15],利用ANSYS程序的接触单元来进行接触分析。将交界面处的土体表面作为接触面,坝体表面刚度比土体的大,将其作为目标面,在接触面上形成接触单元,目标面上形成目标单元,然后通过相同的实常数将对应的接触单元和目标单元定义为1个接触对,并假定接触面上存在库仑摩擦。通过选择合理的参数,可实现土与坝体界面上的黏结、滑移、脱离、再闭合的状态模拟。
3 土−堆石坝体系动力特性
3.1 有限元模型的建立与计算参数的选取
由于土体为半无限体,在有限元计算过程中必须定义人工边界来模拟土体的半无限性质,边界条件及约束条件如图1所示。本文考虑堆石坝的高20 m,坝体基础深5 m。取基础土体宽500 m,深40 m。土体参数取值如表1所示,坝体单元参数如下:面板弹性模量为1.38×109Pa,泊松比为0.40,容重为 25.0 kN/m3,阻尼比取0.10。坝体地震动输入在基底垂直传入单向天津波,其地震波时程曲线如图2所示。
3.2 动力特性
通过对坝体及土体参数的选取,利用ANSYS对土−堆石坝动力相互作用体系进行建模。土与坝体均采用三维实体单元,用前面介绍的等效线性模型模拟土体的非线性特性。考虑土与坝体的材料阻尼以及辐射阻尼效应,同时考虑土与坝体之间接触界面状态非线性对动力特性的影响。在划分网格时,既要保证计算精度,又要考虑计算时间和计算机容量的影响。
通过在基底输入单向天津地震波,得到黏性土不同深度、不同水平位置以及土与坝体不同位置的加速度时程反应曲线,如图3~7所示。
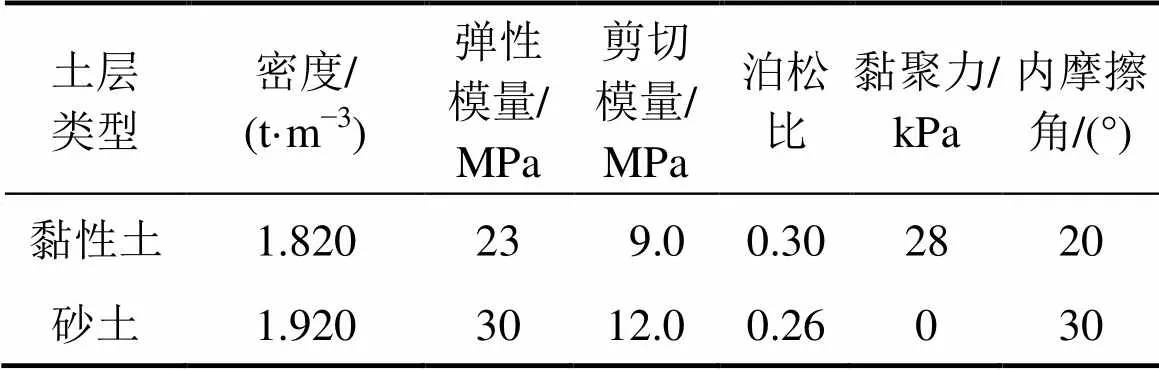
表1 土层物理力学参数
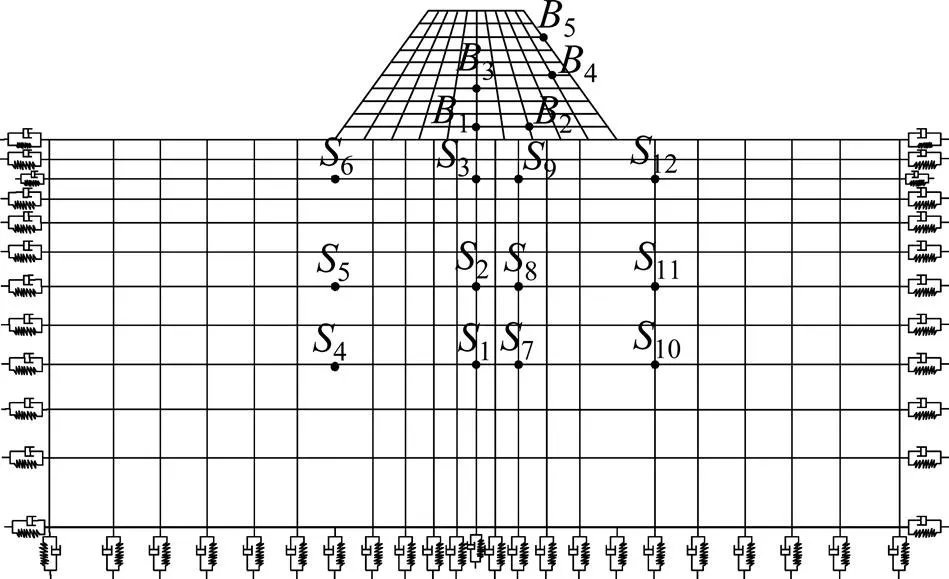
图1 土−堆石坝体系模型边界条件示意图
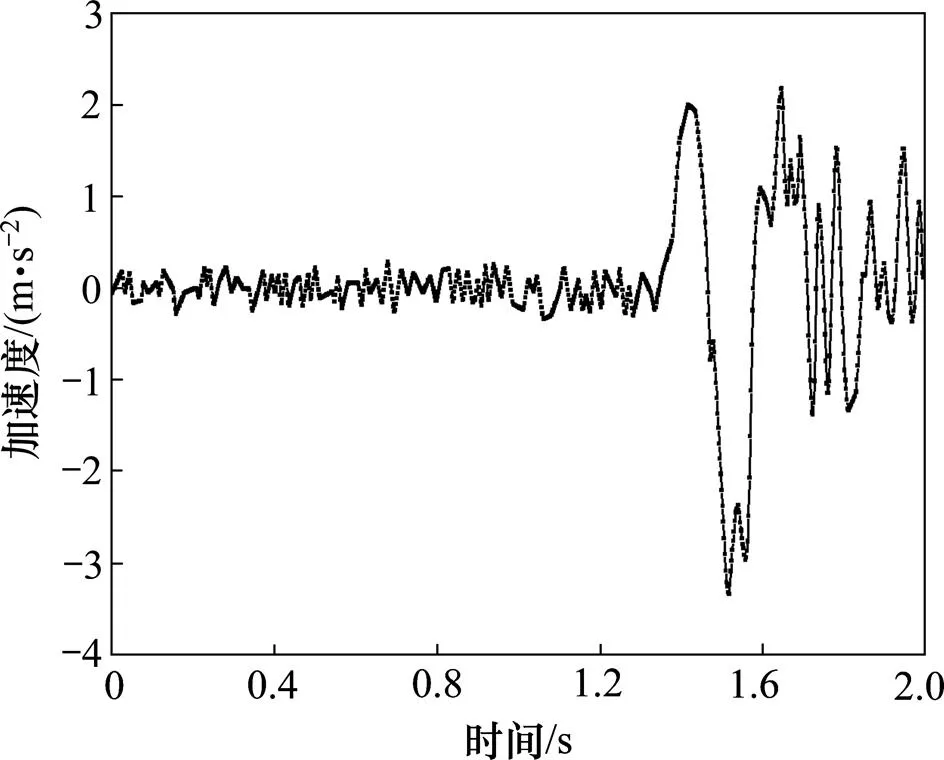
图2 地震波时程曲线
从图3可以看出:远离坝体的土体测点1和2加速度时程变化规律一致,而土体顶部测点3的加速度变化规律与1和2的加速度变化规律正好相反,即在地震波输入初期与末期,测点1的加速度反应比土体中部测点2的加速度反应大,而在地震波输入中期,2的加速度反应比1的加速度反应大。出现此变化规律的原因是在地震波输入初期,土体处于弹性工作阶段,随着地震波由下而上传播,加速度反应也随着波的传播路径减小;而到地震中期,由于土体的非线性性质,出现波的放大效应,导致土体从下部到上部动力反应增大;到震动末期,土体塑性变形后晶体间重新进行排列,其动力反应又随着地震波由下而上而减小。而坝体下土层顶部测点3的加速度动力反应与1和2的加速度动力反应正好相反。这是由于土体受到上部坝体的约束,两者之间的相互作用导致土体反应与下部自由土体的变化规律不一致,这也正好说明了考虑土−坝动力相互作用的重要性。

1—S1;2—S2;3—S3

1—S3;2—B1
从图4可以看出:坝底中部与土体上层中部测点的加速度反应变化规律一致,且幅值相差不大,但土体的加速度幅值在地震中后期比坝体的大。这是因为坝体刚度与土体刚度相差较大,在地震波幅值输入不变的情况下,由于坝体与土体接触部位的相互作用,由此产生的接触阻尼会消耗一部分能量,因而传播到坝体上的地震波能量减小,其动力反应也相应地比土体的小。
图5所示坝体右侧下方土体测点9与竖向相应坝体位置2的加速度时程曲线变化规律一致,地震波输入初期与后期坝体的动力反应均比土体的大,峰值出现在震动后期,而震动中期土体反应比坝体的略大。这是因为地震波从基底中部输入,向周围传播的过程中土的非线性会放大波的震动效应,导致上部坝体内加速度峰值比离震源较近的土体的加速度峰值大。
对比图6和图7中坝体中部及边部竖向相应位置测点加速度时程曲线可以看出:在震动初期与后期,坝体上面的测点加速度反应均比下面测点加速度反应大,且峰值均出现在震动后期,只有在震动中期,坝体下部测点比上部测点的动力反应强,且相差幅度较大。从图6和图7中的1,3,4和5时程曲线可以看出:随着坝体高度的增加,其加速度幅值也相应增大,且竖向位置的变化规律基本相似。
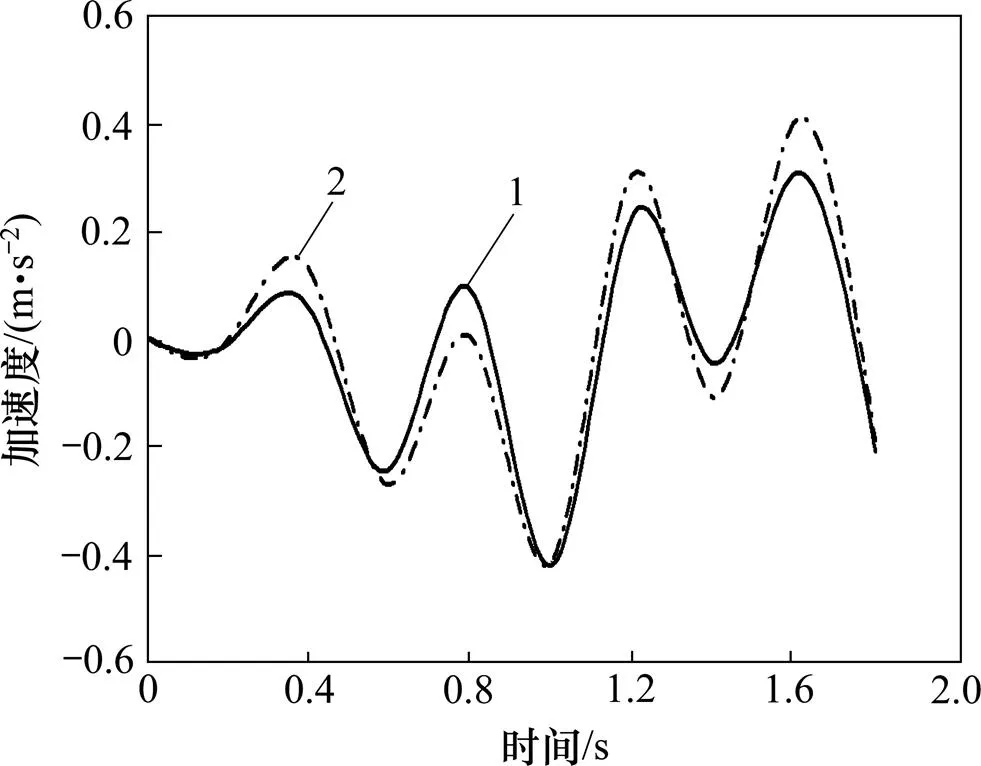
1—S9;2—B2
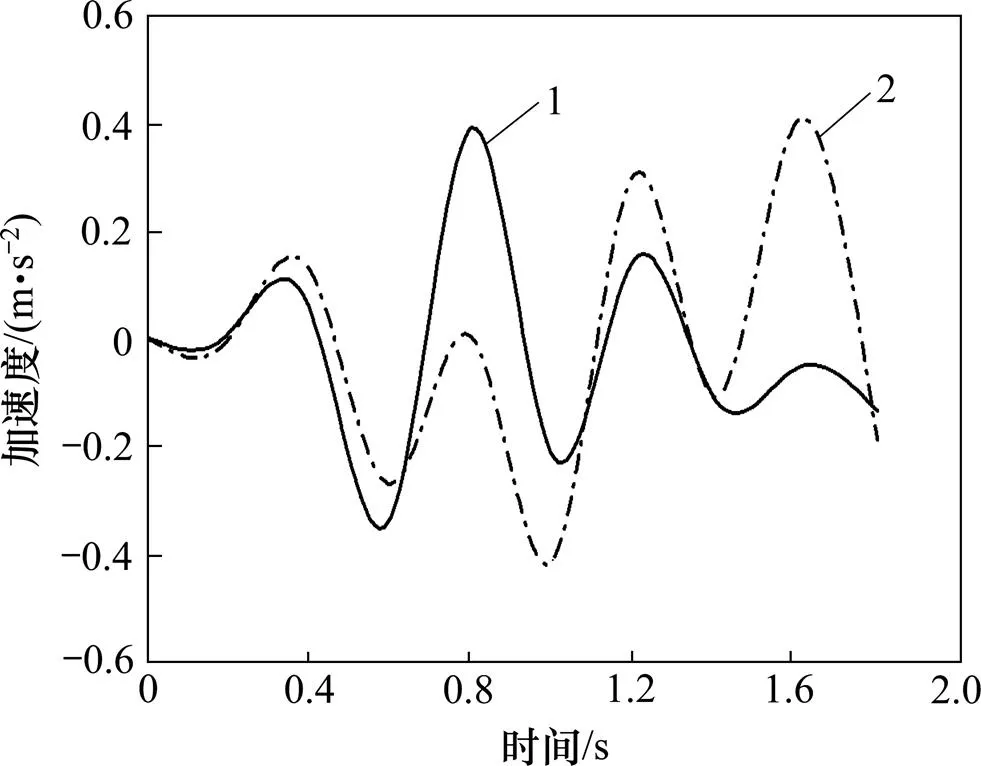
1—B1;2—B3

1—B4;2—B5
图8~10所示为砂土不同深度位置测点的位移时程曲线。从图8和图9可以看出:随着土体深度增加,其位移反应幅值相应增大,土层上部即接近坝体的土体位移反应要小很多,且其时程变化规律与土体下部与中部的相反,幅值变化峰值均出现在震动初期或后期。这说明在震动中期,由于土体非线性以及土与坝体间的接触非线性产生阻尼效应,对地震动能量的消耗起到了重要作用。
从图10可以看出:上、下3个测点的位移反应变化规律基本一致,且峰值均出现在震动末期。这与坝体下面土体的位移反应变化规律不同。土层上部测点位移反应变化与坝体下土体的变化相反,且3个测点的位移反应幅值比坝体下的土体反应幅值要大很多。这说明土体动力反应不仅与地震波输入有关,而且与坝体与土体间动力相互作用有关。因此,在工程设计过程中,必须考虑地基土与坝体之间的相互作用。

1—S4;2—S5;3—S6

1—S7;2—S8;3—S9
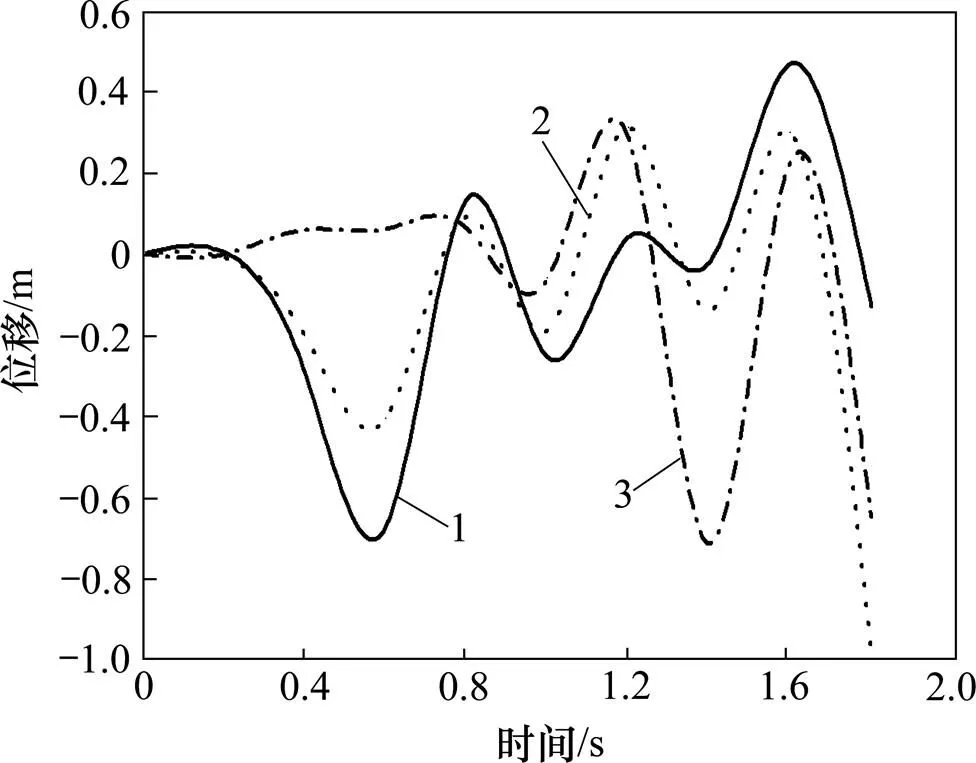
1—S10;2—S11;3—S12
4 结论
1) 在地震波的输入过程中,由于土体的非线性性质出现地震波的放大效应,土体从下部到上部的加速度动力反应逐渐增大,而坝体底部土层加速度动力反应与中下部土层加速度反应正好相反,土体与上部坝体二者之间的相互作用导致土体反应与下部自由土体的变化规律不一致。
2) 由于坝体与土体接触部位的相互作用,由此产生的接触阻尼会消耗一部分能量,导致传播到坝体上的地震波能量减小,其动力反应比土体的小。
3) 随着坝体高度增加,其加速度幅值也相应增加,且在竖向位置其变化规律基本相似,表明坝体动力反应不仅与土的性质有关,而且与坝体高度和位置有关。
4) 随着土体深度的增加,土体位移反应幅值相应增大,土层接近坝体的土体位移反应较小,其时程变化规律与土体中下部的相反,峰值均出现在震动初期或后期,这说明土体非线性以及土与坝体间的接触非线性阻尼效应对地震动能量的消耗起到了重要作用。
在今后的研究中,应考虑深覆盖层地基深度及分布的影响、土中初始剪切模量的影响以及水与坝体间相互作用的影响,以便更全面地考虑土体与坝体以及周围介质间的动力相互作用。
[1] 邱流潮, 刘桦. 混凝土坝−基岩地震动力相互作用时域有限元分析[J]. 岩石力学与工程学报, 2005, 24(20): 3713−3718.QIU Liuchao, LIU Hua. Finite element analysis of seismic concrete dam-foundation rock interaction in time domain[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(20): 3713−3718.
[2] Bycroft G N, Mork P N. Seismic response of dam with soil-structure interaction[J]. Journal of Engineering Mechanics, 1987, 113(9): 1420.
[3] Dakoulas P. Nonlinear response of dams founded on alluvial deposits in narrow canyons[J]. Soil Dynamics and Earthquake Engineering, 1990, 9(6): 301.
[4] Seiphoori A, MohsenHaeri S, Karimi M. Three-dimensional nonlinear seismic analysis of concrete faced rockfill dams subjected to scattered P, SV, and SH waves considering the dam-foundation interaction effects[J]. Soil Dynamics and Earthquake Engineering, 2011(31): 792−804.
[5] 潘家军, 王观琪, 江凌, 等. 基于ABAQUS 的高混凝土面板堆石坝地震反应三维非线性分析[J]. 水力发电学报, 2011, 30(6): 80−84.PAN Jiajun, WANG Guanqi, JIANG Ling, et al. ABAQUS three-dimensional nonlinear analysis of seismic responses of high CFRD[J]. Journal of Hydroelectric Engineering, 2011, 30(6): 80−84.
[6] Alembagheri M, Ghaemian M. Damage assessment of a concrete arch dam through nonlinear incremental dynamic analysis[J]. Soil Dynamics and Earthquake Engineering, 2013(44): 127−137.
[7] 周建烽, 王均星, 陈炜, 等. 线性与非线性强度的土石坝坝坡稳定分析下限法[J]. 岩土力学, 2015, 36(1): 233−239.ZHOU Jianfeng, WANG Junxing, CHEN Wei, et al. Lower bound method for slope stability of earth-rockfill dam with linear and nonlinear strengths[J]. Rock and Soil Mechanics, 2015, 36(1): 233−239.
[8] Zhao P P, Shao M A, Melegy A A, et al. Soil water distribution and movement in layered soils of a dam farmland[J]. Water Resource Management, 2010(24): 3871−3883.
[9] Lizarraga H S, Lai C G. Effects of spatial variability of soil properties on the seismic response of an embankment dam[J]. Soil dynamics and Earthquake Engineering, 2014(64): 113−128
[10] 何益斌, 夏栋舟, 黄欣荣, 等. 土−桩−框架结构动力相互作用非线性有限元模拟[J]. 沈阳建筑大学学报(自然科学版), 2008, 24(3): 428−432.HE Yibin, XIA Dongzhou, HUANG Xinrong, et al. Nonlinear finite element analysis of soil-pile-frame structure-interaction system[J]. Journal of Shenyang Jianzhu University (Natural Science), 2008, 24(3): 428−432.
[11] Martin P P. Nonlinear method for dynamic analysis of ground response[D]. Berkeley: University of California, 1975: 75−76.
[12] Hardin B O, Drnevich V P. Shear modulus and damping in soil measurement and parameter effects[J]. Journal of the Soil Mechanics and Foundation Engineering Division, ASCE, 1972, 98(6): 603−624
[13] 孙静. 岩土动剪切模量阻尼试验及应用研究[D]. 哈尔滨: 中国地震局工程力学研究所, 2004: 34−38. SUN Jing. Laboratory experimental and application study on dynamic shear modulus ratio and damping ratio of soils[D]. Harbin: China Seismological Bureau. Institute of Engineering Mechanics, 2004: 34−38.
[14] 冯领香,魏建国, 王森林, 等. 一种可自调步长的改进Newmark算法[J]. 河北农业大学学报, 2004, 27(3): 111−114. FENG Lingxiang, WEI Jianguo, WANG Senlin, et al. The improved Newmark algorithm with adaptive step size[J]. Journal of Agricultural University of Hebei, 2004, 27(3): 111−114.
[15] 许美, 李黎, 齐正斌. 面板堆石坝有限元接触问题模拟方法研究[J]. 人民长江, 2008, 39(5): 82−84. XU Mei, LI Li, QI Zhengbin. Research on simulation method for contact issue of faced rockfill dam by limit element[J]. Yangtze River, 2008, 39(5): 82−84.
(编辑 陈灿华)
Dynamic characteristics of soil-rockfill dam-dynamic-interaction(SRDI) system based on nonlinearity of soil
XIA Dongzhou1, LIU Yingzhi1, LIU Jianhua2
(1. School of Civil Engineering and Architecture, Changsha University of Science and Technology,Changsha 410114, China;2. School of Traffic and Transportation Engineering, Changsha University of Science and Technology,Changsha 410114, China)
Based on Davidenkov soil model with proper parameters, the simulation of soil nonlinearity was realized by finite element method. The dynamic property of soil-rockfill dam-dynamic-interaction(SRDI) system was studied by ANSYS finite element method, and some problems such as the boundary condition of soil, state nonlinearity of contact boundary between soil and dam, radiation damping of soil, and the coupling damping ratio of soil and dam were considered. The results show that acceleration and displacement of soil increase sharply with the decrease of soil depths, and the dynamic response decrease due to the material damping and contact boundary damping of soil and dam, which improves the earthquake-resistance capability of soil-rockfill dam-interaction system, and provides reference for rockfill dam design and practice.
nonlinearity; soil-rockfill dam-dynamic-interaction (SRDI); radiation damping; earthquake-resistance capability
10.11817/j.issn.1672-7207.2015.09.043
TV641.4
A
1672−7207(2015)09−3481−07
2015−01−07;
2015−03−12
国家自然科学基金资助项目(51378083,51408060);湖南省自然科学基金资助项目(13JJ3071) (Projects(51378083, 51408060) supported by the National Natural Science Foundation of China; Project(13JJ3071) supported by the Natural Science Foundation of Hunan Province, China)
夏栋舟,博士,讲师,从事土−结构动力相互作用与抗震防灾减灾等研究;E-mail: 16400386@qq.com
