列车撞击荷载下盾构隧道双层衬砌管片结构的动力响应特性
2015-10-13晏启祥李彬张蒙陈诚
晏启祥,李彬,张蒙,陈诚
列车撞击荷载下盾构隧道双层衬砌管片结构的动力响应特性
晏启祥1,李彬1,张蒙2,陈诚1
(1. 西南交通大学交通隧道工程教育部重点实验室,四川成都,610031;2. 中铁工程设计咨询集团有限公司,北京,100020)
通过建立三维列车编组撞击有限元模型,获得不同列车编组、列车行驶速度、斜向撞击角度下列车的脱轨撞击荷载时程曲线。采用HHT时间积分法和混凝土塑性损伤模型,研究双层衬砌在不同列车撞击速度和撞击角度下,管片衬砌的应力、变形、速度、加速度、拉压损伤因子及损伤面积等动力响应。研究结果表明:列车撞击荷载主要与列车行驶速度、斜向撞击角度以及列车编组数量有关;撞击力时程曲线在一定条件下出现第2个峰值,动力响应随着列车撞击速度和撞击角度的增大而增大,受拉损伤平均值及其最大值均大于受压损伤平均值和最大值,得出拉压损伤与撞击速度和角度的相互关系。
双层衬砌;列车撞击荷载;管片衬砌结构;动力响应;拉压损伤
目前,国内高速列车的运行安全已日益引起人们的高度关注,高速列车可能脱轨撞击有较大弯道和坡道的盾构隧道并导致隧道结构被破坏,这一威胁已在我国高速铁路建设背景下逐渐显现。国内公路盾构隧道采取防撞墙、防撞墩等非隧道本体结构来应对车辆撞击问题。对于整体质量大、速度高的列车编组,通常采用在管片衬砌内部模筑二次衬砌形成的双层衬砌结构加以应对,如设计目标速度为350 km/h的广深港客运专线狮子洋隧道、沪通铁路黄浦江水下隧道及论证中的琼州海峡跨海通道隧道方案等。尽管国内已经认识到水下盾构隧道管片衬砌遭受列车碰撞的可能性,并采取双层衬砌的防撞措施,但防撞衬砌的设计基本靠经验进行,缺乏应有的理论和实践依据。由于目前国内缺乏对双层衬砌撞击动力学及其防撞效果的研究,尚未揭示不同列车撞击荷载下二次衬砌对管片衬砌保护程度,因此,开展不同列车撞击荷载下盾构隧道双层衬砌管片结构的动力响应特性的研究显得很有必要。国内外近20 a来一直在研究列车被动防护技术,1997年美国制定列车撞击相关安全规范,对单节车辆与刚性墙撞击到列车多体撞击进行大量研究[1];田口真[2]在美国科罗拉多州进行单台整车的撞击试验;姚松等[3]模拟薄壁结构的车辆吸能部件碰撞,并将研究成果成功应用在吸能列车上,取得较好的效果;房加志等[4]利用ABAQUS有限元软件探讨高速列车铝合金材料的耐撞性。上述研究基本都是关注车辆的耐撞性,通过事先假定撞击荷载进行研究,目的是开展列车的防撞性设计以保护车上人员的安全。在混凝土或钢筋混凝土材料的冲击力学研究方面,目前主要集中在结构混凝土材料动态本构模型上,如李兆霞 等[5−6]提出钢筋混凝土材料含有损伤的黏塑性本构模型;Burlion等[7]提出一种基于损伤与塑性相耦合的本构模型。由于缺乏对混凝土材料在冲击荷载作用下破坏机制的全面认识,至今仍未有一种普遍接受的材料本构模型。由于南水北调总干渠穿黄隧洞初步设计拟采用双层衬砌,我国在前期开展了少量有关双层衬砌力学特性的研究,并提出双层衬砌抗压缩模型、局部抗弯模型和抗剪压模型等[8],但国内对双层衬砌力学特性的认识和二次衬砌的具体作用依然没有一致的看法[9−11]。目前,国内列车与隧道的相互作用主要在研究隧道断面对高速列车风的影响以及高速列车风对隧道及其内部设施的影响上,如施成华等[12]研究高速铁路隧道内列车风对接触网安全性的影响,尚未有列车脱轨碰撞荷载和撞击荷载下双层衬砌盾构隧道的动力特性及其损伤评估的相关成果。鉴于此,本文作者基于动力学以及损伤分析理论,建立三维列车编组有限元模型,获得不同因素影响下的列车撞击荷载曲线,研究荷载作用下双层衬砌盾构隧道的动力响应,以揭示二次衬砌对隧道的保护作用。
1 动力学求解及损伤分析理论
采用Hilber,Hughes和Taylor时间积分法(简称为HHT法)[13]求解列车脱轨撞击结构动态响应。HHT时间积分法是由最基本的Newmark时间积分法推演而来,运用隐式HHT时间积分法可有效解决结构非线性动态问题,其对任意时间步长都具有很好的稳定性。将结构体系时刻的达朗伯尔力,与,时刻静力的加权平均值相平衡,其中为计算中某一时刻,为时间推进计算中下一时刻,得HHT时间积分法平衡方程及其位移和速度如下:
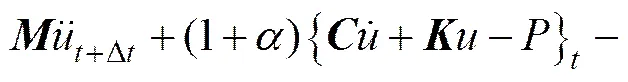
式中:为质量矩阵;为阻尼矩阵;为刚度矩阵;为列车撞击荷载;,和分别为系统位移、速度和加速度。和由权重因子决定:
式中:t为拉损伤因子;为应变与峰值应变之 比;,为拉应力对应的拉应变,为与峰值拉应力对应的峰值拉应变,;,t为峰值拉应力。
在受压条件下,压损伤因子c为
式中:c为压损伤因子;,为压应力对应的压应变,为与峰值压应力对应的峰值压应变,,c为峰值压应力;;。
对于C50混凝土的管片衬砌,其弹性模量为 34 500 MPa,泊松比为0.2,材料进入塑性后应力与非弹性应变、损伤因子与非弹性应变的相互关系见表1。

表1 管片混凝土的拉压损伤演化参数
2 列车撞击荷载的确定
由于国内尚未有列车脱轨实例和相关试验数据,因此,采用数值分析法近似获取列车撞击荷载,通过建立简化的列车−刚性墙撞击三维模型得到近似的撞击力时程曲线。列车编组的材料参数如表2所示,采用薄壳单元建立铝合金型材车体模型,用嵌入泡沫芯材和玻璃钢等型材实现近似等效的车体刚度和相似的质量分布。列车编组车厢之间的连接挂钩用非线性弹簧来模拟,弹簧的刚度和阻尼参数根据国产密接式车钩缓冲装置力学性能曲线确定[15],弹簧刚度参数和阻尼参数分别为2 000 kN/m和40 kN∙s/m。

表2 列车材料参数
采用8,12与16节这3种编组数量,50,100,150,200,250和300 km/h共6种撞击速度,5.0°,7.5°,10.0°,12.5°,15.0°和17.5° 这6种撞击角度构成的108种交叉组合对相应撞击力时程进行分析。图1所示为8,12和16节3种编组的列车在300 km/h撞击速度、斜向撞击角度为17.5°的撞击刚性墙的撞击力时程曲线。由图1可以看出:3种编组的撞击力时程曲线趋势相同,数值接近,相同撞击速度和撞击角度下3种编组的撞击力时程曲线表现出相同的特点,说明列车编组的撞击力时程曲线主要与前几节车厢有关,当列车编组数超过5节后,与列车编组数的相关性减小,原因在于撞击过程极短,后续车辆的惯性力通过车钩传递到机车撞击部位时已经是撞击过程的后段,难以形成叠加效应。由于难以罗列108种交叉组合的列车撞击时程曲线,只代表性给出8节编组列车以12.5°和不同速度斜向撞击的撞击力时程曲线,以及8节列车编组以200 km/h和不同撞击角度撞刚性墙获取的近似撞击力时程曲线,分别如图2和图3所示。
从图2和图3可以看出:在同一撞击角度下,随列车撞击速度增大,撞击力时程曲线上的撞击力整体增大,其撞击持续时间也越长;在同一撞击速度下,斜向撞击角度越大,其撞击力时程曲线上的撞击力也越大。撞击力在撞击瞬间急剧增大并达到最大值,随后急速减小并震荡持续波动一定时间,当角度超过12.5°或列车速度超过200 km/h时,撞击力时程曲线还会出现第2个峰值,撞击过程作用时间根据撞击速度和角度的不同而不同,但基本处于25~40 ms。

列车编组/节:1—8;2—12;3—16

撞击速度/(km∙h−1):1—50;2—100;3—150;4—200;5—250;6—300
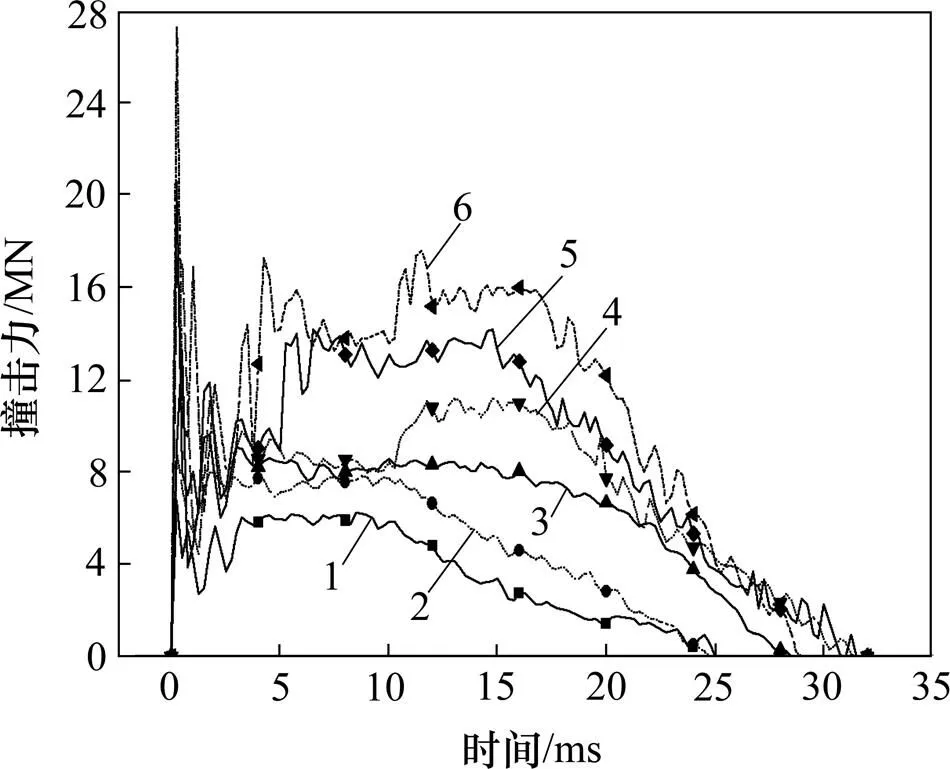
角度/(°):1—5.0;2—7.5;3—10.0;4—12.5;5—15.0;6—17.5

图4 在12.5°撞击角度下不同撞击速度的撞击力第1个峰值

图5 在200 km/h时不同撞击角度的撞击力第1个峰值
3 不同撞击荷载下管片衬砌的动力效应
在获取不同列车行驶速度和撞击角度近似撞击荷载的基础上,选取国内某水下盾构隧道盾构管片衬砌为分析对象,开展双层衬砌外部管片衬砌的撞击动力效应分析。通过对比不同撞击力作用下管片衬砌的动力响应,分析撞击速度和撞击角度对管片衬砌动力响应的影响。撞击力时程曲线选用8节编组在12.5°撞击角度下不同撞击速度,以及8节编组在200 km/h撞击速度下不同撞击角度。将获得的撞击力按实际撞击位置和作用范围以平均面力的近似形式施加在二次衬砌上。该隧道设计采用双层衬砌结构型式,隧道外径为10.30 m、内径为8.74 m、管片厚度为0.48 m、幅宽为2.00 m、混凝土二次衬砌厚度为0.30 m,所衬砌断面如图6所示。隧道周边围岩为第4系上更新统Q3和全新统Q4沉积物,主要由砂性土、风化泥质粉砂等组成。
他无意与小涵争辩。“小涵理论”有着众多的支持者,他甚至赞成其中的某些观点。不能相爱,还能相处。如果连相处都成为困难的事情,婚姻也就随之解体。他和小涵的相处是静态相处,没有过多纠缠不清的热度。小涵说要外出,他会奉献一句玩得开心;他告诉小涵要出门,小涵会回一句,我在家,你放心去吧。半夜回来,更不需要多言,他们各有各的房间。
隧道围岩采用M−C弹塑性本构关系,管片衬砌和二次衬砌采用前述的塑性损伤本构模型。模型边界采用弹簧−阻尼器系统人工边界,用连续分布的并联弹簧−阻尼器系统表示。管片衬砌混凝土采用C50混凝土,管片衬砌环间接头采用抗弯刚度等效的原则,通过弱化环间10 cm长混凝土弹性模量的方式近似模拟。砂性土、风化泥质粉砂、管片衬砌和二次衬砌分析参数如表3所示。围岩衬砌分析模型长×宽×高为90 m×60 m×60 m,如图7所示。
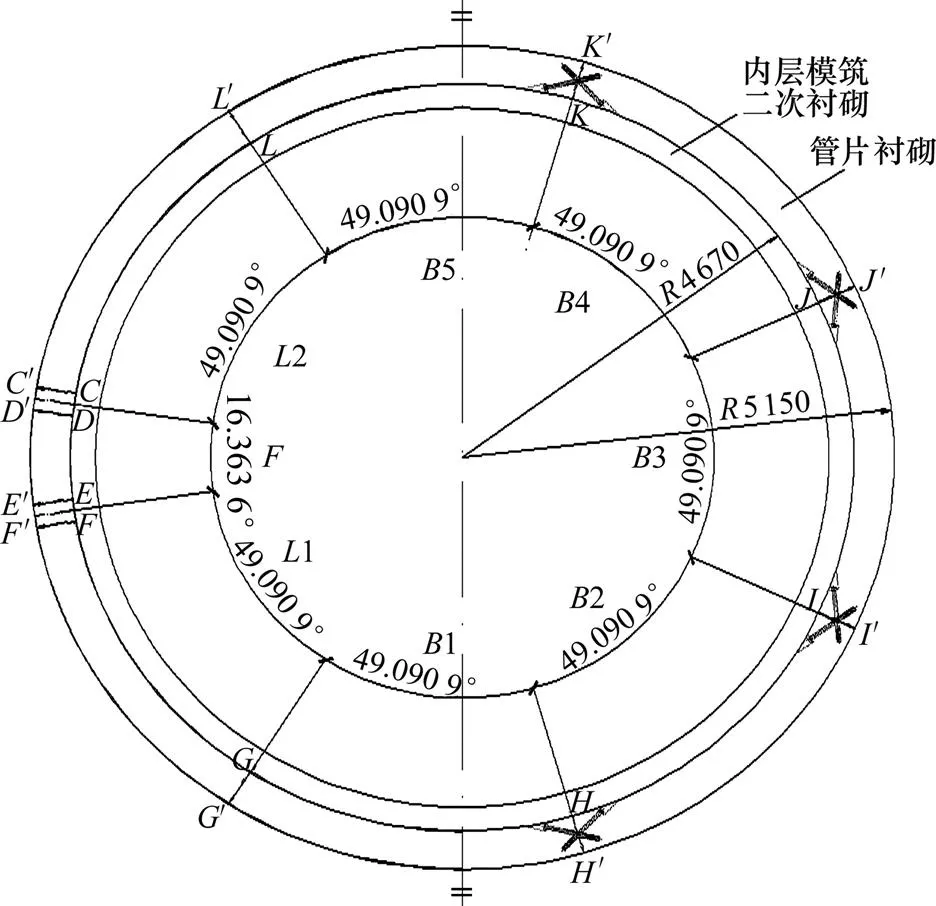
图6 盾构隧道双层衬砌

表3 基本材料参数

(a) 有限元三维模型网格图;(b) 人工边界等效弹簧−阻尼器系统
选取管片衬砌内侧一系列点作为数值分析特征点分析。以二次衬砌撞击区域中心横向水平对应的管片衬砌点为基点,水平纵向前后两侧等距离各取7个数值分析提取点,间距为0.5 m,数值分析提取点1~15位置如图8所示,其中,撞击中心点对应管片衬砌编号为8,模拟列车从左至右行驶并斜向12.5°撞击在二次衬砌上。
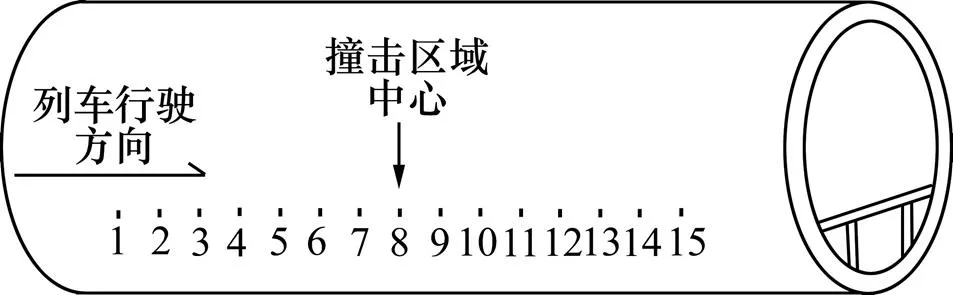
图8 数值分析提取点示意图
3.1 不同撞击速度
图9所示为撞击角度为12.5°时不同撞击速度下管片衬砌各数值提取点的峰值应力、位移、速度和加速度图。由图9可以看出:随着撞击速度的增大,管片衬砌峰值应力、位移、速度和加速度随之增大,在时速300 km/h的条件下,管片衬砌峰值应力、位移、速度和加速度最大值分别达34.5 MPa,6.75 mm,1.85 m/s和3 450 m/s2;随着撞击速度的增大,各峰值不断增大,但增幅在每个速度区间有所不同。
相同撞击速度下,各数值提取点的峰值位移、速度和加速度以撞击区域中心前方1.0 m的位置10最大,而在150 km/h以下时,峰值应力以撞击点中心区域位置8最大,当撞击速度大于150 km/h时,峰值应力可能出现在前方位置9或后方位置7。
图10所示为不同撞击速度下管片衬砌受压、受拉损伤平均值,受压、受拉损伤面积与撞击速度的关系。从图10可以看出:受压损伤平均值随撞击速度的增长表现为平稳增长,而受拉损伤值在50~100 km/h时对撞击速度较为敏感,速度从50 km/h增大到100 km/h时,受拉损伤平均值均急剧增大,但当撞击速度为100~300 km/h时增长不明显;受拉损伤面积随着撞击速度的增大表现为较平稳的增长;受压损伤面积在50~100 km/h时对撞击速度较为敏感,当撞击速度从50 km/h增大到100 km/h时,受压损伤面积急剧增长,但当撞击速度为100~300 km/h时,受压损伤面积增长较缓慢。总体而言,受拉损伤平均值和受拉损伤面积随着撞击速度的增大迅速上升到较高水平,之后缓慢增长,而受压损伤平均值和受拉损伤面积则随着撞击速度的增大而慢慢增长。

(a) 应力;(b) 位移;(c) 速度;(d) 加速度撞击速度/(km∙h−1):1—50;2—100;3—150;4—200;5—250;6—300

(a) 损伤平均值;(b) 损伤面积
1—受压损伤;2—受拉损伤
图10 管片衬砌拉压损伤与速度的关系
Fig. 10 Relationship between tensile and compressive damage of segment lining and impact velocity
3.2 不同撞击角度

(a) 应力;(b) 位移;(c)速度;(d)加速度
撞击角度/(°):1—5.0;2—7.5;3—10.0;4—12.5;5—15.0;6—17.5
图11 不同撞击角度下管片衬砌各提取点峰值应力、位移、速度和峰值加速度
Fig. 11 Peak stress, peak displacement, peak velocity and peak acceleration of segmental lining extraction point at different impact angles
在相同撞击角度下,各数值提取点的峰值位移、速度和加速度以撞击区域中心前方1.0 m的位置10最大,而峰值应力在10.0°以下时以撞击点中心区域位置8最大,当撞击角度大于10.0°时,峰值可能出现在前方的位置9或后方的位置7。
表4所示为在200 km/h撞击速度下不同撞击角度管片衬砌的拉压损伤平均值、最大值及其对应的损伤面积。由表4可见:随着斜向撞击角度的增大,管片衬砌的拉压损伤平均值、最大值及其对应的损伤面积都不断增大。从总体上看,受拉损伤平均值及其最大值均大于受压损伤平均值和最大值,受拉损伤平均值及其最大值在撞击角度达到7.5°后,继续增大撞击角度,其值分别在0.287 3~0.319 2,0.861 8~0.957 6之间变化,变化幅度不大,而受压损伤平均值及其最大值随撞击角度的增大而增大。受拉损伤面积同样随撞击角度的增大而增大,从5.0°对应的8.5 m2逐渐增大到17.5°对应的25.5 m2,而受压损伤面积只从5.0°对应的8.5 m2小幅变化到17.5°对应的13.5 m2。

表4 不同撞击角度下各参数值
4 结论
1) 列车撞击荷载主要与列车行驶速度、斜向撞击角度以及列车编组数有关,当列车编组超过5节时,编组数对撞击荷载的影响逐渐减弱。列车撞击力在撞击瞬间急剧增大并达最大值,随后急速减小并震荡持续波动一定时间。当撞击角度超过12.5°或列车速度超过200 km/h时,撞击力曲线还会出现第2个峰值;撞击荷载作用时间与列车撞击速度和角度有关,但基本处于25~40 ms。
2) 管片衬砌的各位置的峰值应力、位移、速度和加速度随着列车撞击速度的增大而增大。受拉损伤平均值及其最大值均大于受压损伤平均值和最大值。受拉损伤平均值和受拉损伤面积随着撞击速度的增大迅速上升到较高水平,之后缓慢增长,而受压损伤平均值和受拉损伤面积则随着撞击速度的增大而逐渐 增长。
3) 管片衬砌的各位置的峰值应力、位移、速度和加速度随着列车撞击角度的增大而增大。在相同撞击速度下,随斜向撞击角度的增大,管片衬砌的拉压损伤平均值、最大值及其对应的损伤面积都不断增大;受拉损伤平均值及其最大值均大于受压损伤平均值和最大值,受拉损伤平均值及其最大值随撞击角度增大快速增大,之后缓慢变化,而受压损伤平均值及其最大值随撞击角度无明显急速上升过程,表现出渐进增大趋势。
[1] Müller F. 轻轨车辆的制造[J]. 国外铁道车辆, 2000, 37(5): 7−11. Müller F. Manufacture of light rail vehicles[J]. Foreign Rolling Stock, 2000, 37(5): 7−11.
[2] 田口真. 铁道车辆抗冲撞结构的开发[J]. 国外铁道车辆, 2003, 40(6): 23−27. TIAN Kouzhen. Development of crashworthy structure of rolling stock[J]. Foreign Rolling Stock, 2003, 40(6): 23−27.
[3] 姚松, 田红旗. 车辆吸能部件的薄壁结构碰撞研究[J]. 中国铁道科学, 2001, 22(2): 55−60. YAO Song, TIAN Hongqi. Crash research on thin-shelled structure as vehicle energy-absorbing components[J]. China Railway Science, 2001, 22(2): 55−60.
[4] 房加志, 刘金朝, 焦群英, 等. 铁路客车结构大变形碰撞特性的仿真研究[J]. 中国农业大学学报, 2004, 9(4): 76−78. FANG Jiazhi, LIU Jinchao, JIAO Qunying, et al. Simulation of collision characteristics of train vehicle with large deformation[J]. Journal of China Agricultural University, 2004, 9(4): 76−78.
[5] 李兆霞. 一个综合模糊裂纹和损失的混凝土应变软化本构模型[J]. 固体力学学报, 1995, 16(1): 22−30. LI Zhaoxia. A viscoplastic model combined damage and smeared crack for softening of concrete[J]. Chinese Journal of Solid Mechanics, 1995, 16(1): 22−30.
[6] 宁建国, 商霖, 孙远翔. 混凝土材料冲击特性的研究[J]. 力学学报, 2006, 38(2): 199−208. NING Jianguo, SHANG Lin, SUN Yuanxiang. Investigation on impact behavior of concrete[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(2): 199−208.
[7] Burlion N, Fabrice G, Gilles P C, et al. Compaction and tensile damage in concrete: Constitutive modeling and application to dynamics[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 183(3): 291−308.
[8] 张厚美, 过迟, 吕国梁. 盾构压力隧洞双层衬砌的力学模型研究[J]. 水利学报, 2001, 32(4): 28−33, ZHANG Houmei, GUO Chi, LÜ Guoliang. Mechanical model for shield pressure tunnel with secondary linings[J]. Journal of Hydraulic Engineering, 2001, 32(4): 28−33.
[9] 张厚美, 连烈坤, 过迟. 盾构隧洞双层衬砌接头相互作用模型[J]. 岩石力学与工程学报, 2003, 22(1): 70−74. ZHANG Houmei, LIAN Liekun, GUO Chi. Joint interaction model for shield tunnel segment reinforced by secondary linings[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(1): 70−74.
[10] 赵德安, 雷晓燕, Swoboda G. 单、双层衬砌隧道的非线性有限元分析[J]. 中国公路学报, 2003, 16(1): 62−67. ZHAO Dean, LEI Xiaoyan, Swoboda G. Nonlinear FEM analysis for single and double lining tunnels[J]. China Journal of Highway and Transport, 2003, 16(1): 62−67.
[11] 晏启祥, 程曦, 何川, 等. 水压条件下盾构隧道双层衬砌力学特性分析[J]. 铁道工程学报, 2010, 144(9): 55−59. YAN Qixiang, CHENG Xi, HE Chuan, et al. Analysis of mechanical properties of double-layered lining of shield tunnel under water pressure[J]. Journal of Railway Engineering, 2010, 144(9): 55−59.
[12] 施成华, 杨伟超, 彭立敏, 等. 高速铁路隧道列车风作用下接触网安全性分析[J]. 中南大学学报(自然科学版), 2012, 43(9): 3652−3658.SHI Chenghua, YANG Weichao, PENG Limin, et al. Analysis of catenary’s safety under train wind action in high-speed railway tunnel[J]. Journal of Central South University (Science and Technology), 2012, 43(9): 3652−3658.
[13] 李丽. 基于ABAQUS的高速公路隧道地震动力响应研究[D]. 成都: 西南交通大学土木工程学院, 2009: 11−15. LI Li. Study on seismic dynamic response of expressway tunnel based on ABAQUS[D]. Chengdu: Southwest Jiaotong University. School of Civil Engineerin g, 2009: 11−15.
[14] GB 50010—2002, 混凝土结构设计规范[S]. GB 50010—2002, Code for design of concrete structures[S].
[15] 王娜娜, 马卫华. 自动车钩的弹簧刚度和阻尼系数对列车纵向动力学的影响[J]. 内燃机车, 2010(9): 1−3. WANG Nana, MA Weihua. Influence of spring stiffness and damping coefficient of automatic coupler on the longitudinal dynamics of train[J]. Diesel Locomotives, 2010(9): 1−3.
(编辑 刘锦伟)
Dynamic response of segment structure of double lining shield tunnel under train impact load
YANQixiang1, LI Bin1, ZHANG Meng2, CHEN Cheng1
(1. Key Laboratory of Transportation Tunnel Engineering, Ministry of Education, Southwest Jiaotong University, Chengdu 610031, China;2. China Railway Engineering Consulting Group Co. Ltd., Beijing 100020, China)
A three-dimensional numerical analysis model of the train formation was established to obtain the time-history curves of the train impact force under different train formations, impact velocities and oblique impact angles. Based on HHT time integration scheme and concrete plastic damage model, the dynamic responses of the double lining shield tunnel caused by the impact force under different impact velocities and impact angles were studied, such as stress, displacement, velocity, acceleration, tension & compression damage factor and damaged area of the segment lining. The results show that the impact force is mainly related to the train impact velocity, oblique impact angle and train formation, and the time-history curve of the impact force has a second peak interval under certain conditions. Dynamic response increases with the increase of the impact velocity and impact angle, and the average and maximum value of tensile damage are higher than those of compressive damage, respectively. The relationship between tension & compression damage, the impact velocity and angle are obtained.
double lining; train impact load; segment lining structure; dynamic response; tension and compression damage
10.11817/j.issn.1672-7207.2015.09.049
U451.4
A
1672−7207(2015)09−3527−08
2014−09−02;
2014−11−23
国家自然科学基金资助项目(51178400,51278425,U1134208);教育部新世纪人才支持计划项目(NCET-11-0713) (Projects(51178400, 51278425, U1134208) supported by the National Natural Science Foundation of China; Project(NCET-11-0713) supported by the New Century Talents Project Funded by the Ministry of Education)
晏启祥,博士,教授,博士生导师,从事隧道工程的教学与研究;E-mail: 764365015@qq.com
