负泊松比岩体颗粒流模型及模拟分析
2015-10-13金爱兵王凯杨振伟孟新秋
金爱兵,王凯,杨振伟,孟新秋
负泊松比岩体颗粒流模型及模拟分析
金爱兵,王凯,杨振伟,孟新秋
(北京科技大学土木与环境工程学院,北京,100083)
为了从微观结构角度研究岩体特殊的负泊松比效应,基于颗粒流理论和颗粒流程序(PFC),提出采用颗粒流数值模拟方法。从已知具有负泊松比效应的无机晶体材料出发,研究其内部特殊的微观结构,进而建立符合岩体情况的颗粒流模型。利用所生成模型进行单轴压缩模拟试验,得出泊松比随应力的变化曲线。基于所建模型,对岩体在低荷载水平作用下的负泊松比现象机理进行分析。研究结果表明:当轴压为0~3 MPa时,岩体试样泊松比为负值,最小泊松比为−0.059。模拟结果与室内试验结果大致吻合,验证了该颗粒流模型用于研究岩体负泊松比现象的可靠性。
岩体;负泊松比;PFC;颗粒流模型;微观结构
西蒙∙泊松定义材料负的横向应变与纵向应变之比为泊松比[1]。在通常情况下,材料的泊松比为正值,即材料在纵向拉伸时横向发生收缩。而负泊松比效应是指在材料纵向拉伸时,横向发生膨胀;受压缩时横向发生收缩。根据经典弹性力学,钱伟长等[2]从理论上严格证明在等温条件下各向同性材料的泊松比取值范围为−1~0.5,说明理论上存在负泊松比(negative Poisson’s ratio)物质。目前,在高分子材料领域已经陆续研制出一些具有负泊松比效应的材料。Lakes[3]把1个长×宽×高为110 mm×38 mm×38 mm的普通聚氨酯泡沫放入1个长×宽×高为75 mm×25 mm× 25 mm的铝制模具中,经过一系列室内试验处理后,所得泡孔单元呈内凹(re-entrant)结构,并测出其泊松比为−0.7。目前,有关内凹结构研究较多的是六边形蜂窝材料,除此之外还有其他一些结构模型[4]具有负泊松比效应,如卢子兴等[5]在前人研究基础上提出了一种部分内凹、部分规则的六边形二维多胞材料力学模型,并随之预测了模型泊松比与刚度系数随角度的变化关系,求解出其剪应变量,最终通过能量法计算出该力学模型的本构方程。而关于岩石类材料负泊松比的研究较少。王让甲等[6−7]在对一组不同类别岩样进行单轴压缩试验时,发现出现泊松比为负的情况;基于国内某海底隧道工程的岩体室内实验,涂忠仁等[8]在低荷载水平作用下观察到花岗岩泊松比为负值的现象,并利用Grima等[9−10]在对无机晶体材料研究时提出的“晶粒转动”模型进行了初步解释。但前人并未对岩体微观结构进行深入分析。由于岩石是典型的非均质、非连续材料,采用连续介质力学理论和数值模拟方法对岩体进行分析明显存在着不足,而离散单元法作为求解非连续介质力学问题的一个重要数值分析方法,却可以从微观到宏观对岩体的破坏过程进行模拟分析[11]。为此,本文作者在前人的研究内容和室内试验基础上,从岩体内部的微观结构角度出发,采用PFC程序数值模拟方法对岩体负泊松比现象进行研究 分析。
1 研究方法
根据材料泊松比定义,用公式表达即为
材料的弹性模量、体积模量、剪切模量、纵波速度p和横波速度s与材料泊松比存在如下关系:
1.1 PFC颗粒单元
基于PFC程序,采用颗粒单元构建计算模型,设定颗粒间细观接触参数,模拟介质的基本特性随应力环境的变化。当颗粒间黏结受外部作用影响发生破坏时,颗粒相互分离,实现对岩样破坏过程的模拟。在模拟颗粒黏结破坏过程中,PFC程序提供了2种基本的颗粒黏结模型[12](如图1所示):接触黏结模型和平行黏结模型,两者合称为黏结颗粒模型(BPM)[13]。本文所采用的是接触黏结模型。

(a) 接触黏结模型;(b) 平行黏结模型
由于BPM存在拉压强度比过高及内摩擦角偏低等缺陷,为克服该问题本文采用簇单元模型(CPM,如图2所示)来模拟岩体颗粒,该模型使用不规则的异形颗粒代替BPM介质中的圆形颗粒,通过增大颗粒之间的咬合及摩擦效应,克服BPM中颗粒形状失真所带来的问题[14]。
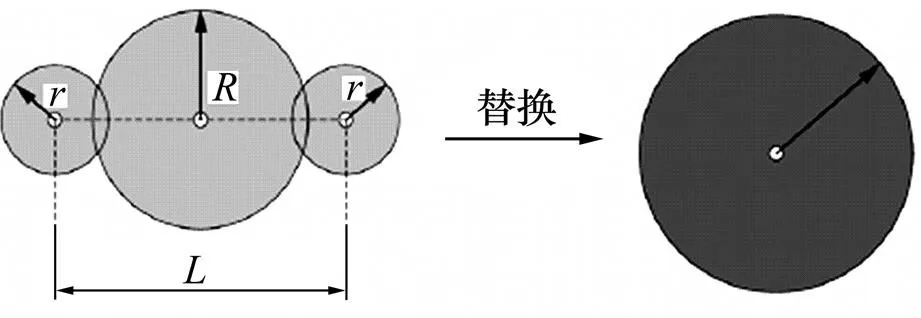
图2 簇单元模型
1.2 负泊松比岩体PFC模型
不少科学工作者已经研制出负泊松比材料,同时还提出了多种理论模型,并对其成因机理进行分析解释。Grima等[9−10]在对一些无机晶体材料研究时发现,某些晶体内部通过彼此之间的铰链连接在一起,并在微观结构上呈方格状排列,据此提出了负泊松比无机晶体材料的“晶粒转动”模型,如图3所示。
根据图3所示的“晶粒转动”模型,假设每个晶体单元的长度为,之间夹角为,则在每个单元内有

(a) 压缩;(b) 拉伸
根据式(1)的定义,泊松比瞬时变化量为
由图3和式(6)可得
联立式(5)~(7),求得该无机晶体材料的理论泊松比值瞬时变化量为−1。
基于图3所示的无机晶体的“晶粒转动”理论模型,对室内试验中所观察到的岩体负泊松比现象进行研究分析。假定部分特殊岩体具有类似图3所示理论模型微观结构,并将该模型转换成可以在离散元软件PFC中使用的颗粒流模型来研究这一现象,具体转换步骤如下:1) 将“晶粒转动”模型中的方格状排列转换成岩石颗粒的圆形球状排列,即将晶体颗粒转换成PFC中的簇单元模型(CPM);2) 将晶体颗粒间起到连接作用的铰链转化成PFC程序中所提供的接触黏结模型;3) 将试样内岩石大颗粒间的空隙用较小颗粒进行填充,进而得到更符合岩体真实情况的颗粒流模型;4) 为避免模拟试验计算结果失真,需消除PFC模型中的悬浮颗粒[15]。
对照“晶粒转动”理论模型(见图3),最终得到的负泊松比岩体颗粒流理论模型如图4所示。
2 颗粒流模拟与实例验证
2.1 颗粒流模型
在已有室内花岗岩试样单轴压缩实验的基础上来进行颗粒流模拟试验。按照国内有关试验规程规 定[16]:抗压试验应采取高径比为2.0~2.5的标准规则试件,为方便建模,本试验中的岩石试样高×直径为120 mm×60 mm。

(a) 压缩;(b) 拉伸;(c) 变换后压缩;(d) 变换后拉伸
本颗粒流模型中,定义岩体试样的墙体共4个,编号为1号、2号、3号和4号,所包围的矩形范围 (高×宽)为120 mm×60 mm。其中,1号和2号墙体为加载墙,3号和4号墙体在前期生成模型时起约束作用,在后期进行单轴压缩模拟试验时将其删除。单轴压缩模拟试验PFC数值试样通过一系列的微观颗粒构建而成。其中:用于替换BPM的簇单元(CPM)大圆颗粒半径=3.62 mm,小圆颗粒半径=0.77 mm,2个小圆颗粒圆心距=4.20 mm(的含义见图2);填充物的颗粒半径采用min~max的高斯分布,其中min=0.38 mm,max=0.40 mm;颗粒之间采用接触黏结模型。对于给定尺寸的CPM模型在区域内部的指定位置均匀生成,总数为72个;而对于给定半径范围的充填物颗粒在空隙区域内随机生成,颗粒总数为6 734个;PFC模型中总的颗粒数为6 806个。
为保证颗粒生成效果及效率,先生成小直径颗粒,再将其半径放大复原[17]。本次颗粒流模拟试验中将与周围颗粒接触数量小于3的颗粒定义为悬浮颗粒,其消除步骤为:1) 搜索悬浮颗粒,将其固定并赋予悬浮颗粒速度为0 m/次;2) 将悬浮颗粒的半径扩大20%使其与周围颗粒充分接触;3) 循环一定步数达到局部受力平衡状态,若悬浮颗粒间最大接触力小于指定容忍值时,则将此悬浮颗粒更改为普通颗粒;4) 当悬浮颗粒间最大接触力大于指定容忍值时,将颗粒半径缩小10%,重复步骤3),以此消除PFC模型中所有悬浮颗粒。最终得到的岩体试样单轴压缩颗粒流模拟试验PFC模型如图5所示。

图5 颗粒流模拟PFC 模型
2.2 模型细观参数
本次研究中模型介质细观参数校核自厦门东通道海底隧道中岩体泊松比出现负值的XASD Ⅲ级围岩(花岗岩)岩样[8],其相关宏观力学参数:单轴抗压强度为50~80 MPa;弹性模量为4.600 GPa;泊松比为0.050。经反复调试匹配,最终得到PFC数值模型的宏观力学参数:单轴抗压强度为58 MPa;弹性模量为 4.230 GPa,泊松比为0.056。此时模型所取细观力学参数如表1所示。模拟结果与试验结果基本一致,可将该组细观力学参数用于实际模型计算[18−20],利用该PFC数值模型能准确地对试样泊松比变化情况进行研究分析。

表1 PFC模型细观力学参数
注:接触黏结法向和切向刚度分别为3.26×108Pa/m和1.27×108Pa/m;法向和切向强度分别为(2×107±5×106) Pa和(2×107±5×106) Pa。
2.3 模拟过程及结果
花岗岩是一种坚硬脆性岩石,本文中PFC模型试样的单轴抗压强度为58 MPa,而本次模拟主要目的是研究低荷载水平作用下岩体的负泊松比现象,所以,本次单轴压缩模拟试验只涉及岩体破坏过程中的裂隙闭合阶段和弹性变形的初级阶段。通过前期模拟计算,确定墙体上的最终法向荷载为6.5 MPa为宜。即在本次颗粒流模拟过程中,当1号和2号墙体上的法向荷载达到6.5 MPa时就停止加载。在颗粒流模拟过程中,由于PFC程序中对加载墙只能施加速率,因此,需要通过不断调整1号和2号墙体的加载速率以控制墙体受力,从而可达到向PFC数值模型施加连续、稳定法向荷载的目的。最终得到PFC模型试样的应力−应变曲线、应变关系曲线和泊松比变化曲线如图6~8所示。模拟试验中纵向应变原始实测数据为负值,为方便作图,将其取为相反数。
从图6~8可知:1) 模拟试验的应力−应变曲线与常规室内单轴压缩试验前期低荷载作用下的应力−应变曲线特征相同,变化规律相吻合;2)段为岩体裂隙闭合阶段,段岩体已处于弹性变形阶段;3) 当PFC模型试样所受荷载较小(本试验中小于3 MPa)时,岩体泊松比为负值;4) 当PFC模型试样所受荷载较大(本试验中大于3 MPa)时,岩体的泊松比逐渐变大,并恢复为正值。
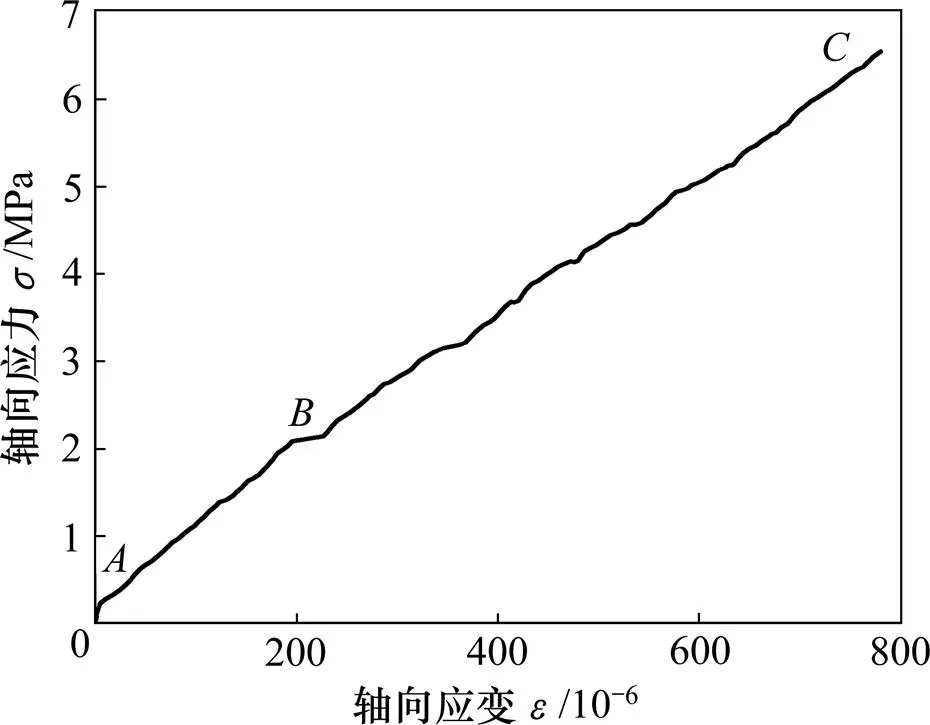
图6 模拟试验应力−应变曲线

图7 模拟试验应变关系曲线

图8 模拟试验泊松比变化曲线
2.4 对比试验
为验证基于颗粒流分析方法的负泊松比岩体PFC模型的可靠性,将模拟实验和室内单轴压缩试验[8]进行对比分析。对比试验中岩石试样为中粗粒黑云母花岗岩,试样纵高×直径为83 mm×50 mm,密度为 2 408 kg/m³。对比试验中相关测试结果如表2所示,对比试验的应变关系曲线如图9所示。
2.5 对比结果
综合颗粒流模拟试验结果与室内对比试验,结果发现:在低荷载水平作用下,部分特殊岩体会出现泊松比为负值的情况。为进一步验证负泊松比岩体颗粒流模型的有效性,将模拟试验与室内试验的泊松比变化曲线进行对比分析,其结果如图10所示。

表2 单轴压缩测试结果

图9 对比试验应变关系曲线
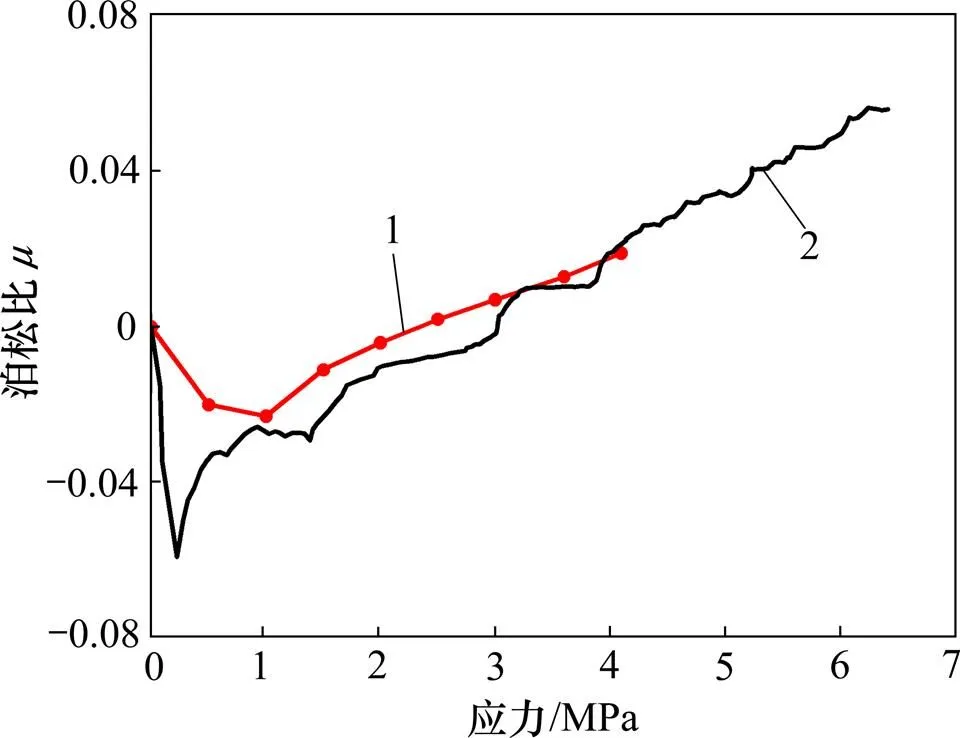
1—模拟试验;2—室内试验
从图10可以看出:1) 2条曲线走向、趋势、变化特征基本相同;2) 当荷载大于3 MPa时2条曲线基本吻合;3) 室内试验时,岩体出现负泊松比现象的荷载区间为0~2.3 MPa,最小泊松比为−0.023(相应轴压为1 MPa),模拟试验此区间为0~3 MPa,最小泊松比为−0.059(相应轴压为0.23 MPa);4) 由于室内试验应力不能连续加载,每次加载量间隔为0.5 MPa,所以,不排除荷载为0~1 MPa的区间内会存在更小的负泊松比,而这可能会使颗粒流模拟试验结果和室内对比试验结果拟合程度更好。
3 负泊松比现象形成机理分析
基于本文所提出的负泊松比岩体颗粒流模型,假定部分特殊岩体具有类似于图4所示的理论模型微观结构,则可对室内试验和模拟试验中所观测到的负泊松比现象进行合理解释。
基于上述假定,对于岩体单轴压缩试验,由图4和图8可知:阶段由于应力比较小,岩体内部结构变化缓慢,岩石颗粒间发生相对旋转、错动,内部孔隙被压密,岩样向内出现“颈缩”的现象,所以,这一阶段测量得到的横向应变为负值,计算得到的泊松比也为负值;阶段应力较大,岩体内部的大部分孔隙压密后又呈现出正常的变形规律,横向应变开始逐渐增大,并恢复为正值,之后计算得到的泊松比也逐渐增大,并恢复为正值。
4 结论
1) 研究了具有负泊松比效应的无机晶体材料,参照其特殊的“晶粒转动”模型,进而建立符合岩体实际情况,具有负泊松比效应的颗粒流(PFC)模型。
2) 基于颗粒流分析方法,利用负泊松比岩体PFC模型进行了数值模拟试验,试验中出现与已有室内试验相同的结果,即部分特殊岩体会出现负泊松比效应。
3)将颗粒流模拟试验与室内试验进行对比,两者的泊松比变化特征相吻合,低荷载时岩体泊松比为负,高荷载时恢复正值,两者结果具有高度相似性,表明本文所提出的负泊松比岩体PFC模型可用于研究岩体的负泊松比效应。
4) 基于部分特殊岩体具有类似于本文所提出负泊松比岩体颗粒流理论模型微观结构的假定,对岩体的负泊松比现象进行分析,即低压压缩时模型颗粒间发生相对旋转、错动,岩样横向出现“颈缩”现象,横向应变为负值,泊松比也为负值。
[1] 史炜, 杨伟, 李忠明, 等. 负泊松比材料研究进展[J]. 高分子通报, 2003(6): 48–57. SHI Wei, YANG Wei, LI Zhongming, et al. Progress of materials with negative Poisson’s ratio[J]. Chinese Polymer Bulletin, 2003(6): 48–57.
[2] 钱伟长, 叶开沅. 弹性力学[M]. 北京: 科学出版社, 1956: 76–79. QIAN Weichang, YE Kaiyuan. Elastic mechanics[M]. Beijing: Science Press, 1956: 76–79.
[3] Lakes R. Foam structures with a negative Poisson’s ratio[J]. Science, 1987, 235(2): 1038–1040.
[4] Smith C W, Grima J N, Evans K E. A novel mechanism for auxetic behavior in reticulated foams: missing rib foam model[J]. Acta Materialia, 2000, 48(17): 4349–4356.
[5] 卢子兴, 赵亚斌. 一种有负泊松比效应的二维多胞材料力学模型[J]. 北京航空航天大学学报, 2006, 32(5): 594–597. LU Zixing, ZHAO Yabin. Mechanical model of two-dimensional cellular materials with negative Poisson’s ratio[J]. Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(5): 594–597.
[6] 王让甲, 樊冀安, 高学之. 岩石负泊松比的探讨[J]. 探矿工程, 1996(4): 17–19. WANG Rangjia, FAN Jian, GAO Xuezhi. Note on rock with negative Poisson’s ratio[J]. Exploration Engineering, 1996(4): 17–19.
[7] 王让甲. 岩石声波分级和岩石动弹性力学参数的分析研究[M]. 北京: 地质出版社, 1997: 96–101. WANG Rangjia. Study on classification of rock’s sound wave and parameters of rock’s dynamic-elastic mechanics[M]. Beijing: Geology Publishing House, 1997: 96–101.
[8] 涂忠仁, 杨强. 岩体负泊松比试验研究[J]. 岩土力学, 2008, 29(10): 2833–2836. TU Zhongren, YANG Qiang. Test research on negative Poisson’s ratio of rock mass[J]. Rock and Soil Mechanics, 2008, 29(10): 2833–2836.
[9] Grima J N, Evans K E. A novel mechanism for generating auxetic behavior in reticulated foams: missing rib foam model[J]. Journal of Material Science Letter, 2000, 19(17): 1563–1565.
[10] Grima J N, Alderson A, Evans K E. An alternative explanation for the negative Poisson’s ratios in α-cristobalite[J]. Materials Science & Engineering A, 2006, 423(2): 219–224.
[11] 蒋明镜, 陈贺, 刘芳. 岩石微观胶结模型及离散元数值仿真方法初探[J]. 岩石力学与工程学报, 2013, 32(1): 15–23. JIANG Mingjing, CHEN He, LIU Fang. A microscopic bond model for rock and preliminary study of numerical simulation method by distinct element method[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(1): 15–23.
[12] Cho N, Martin C D, Sego D C. A clumped particle model for rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(7): 997–1010.
[13] Potyondy D O, Cundall P A. A bonded-particle model for rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(8): 1329–1364.
[14] 余华中, 阮怀宁, 褚卫江. 岩石节理剪切力学行为的颗粒流数值模拟[J]. 岩石力学与工程学报, 2013, 32(7): 1482–1490. YU Huazhong, RUAN Huaining, CHU Weijiang. Particle flow code modeling of shear behavior of rock joints[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(7): 1482–1490.
[15] Itasca Consulting Group. PFC2D(particle flow code in 2 dimensions) fish in PFC2D[M]. R Minneapolis, USA: Itasca Consulting Group, 2008: 20–22, 83–85.
[16] 赵文, 曹平, 章光. 岩石力学[M]. 长沙: 中南大学出版社, 2010: 23–25. ZHAO Wen, CAO Ping, ZHANG Guang. Rock mechanics[M]. Changsha: Central South University Press, 2010: 23–25.
[17] 周喻, 吴顺川, 张晓平. 岩石节理直剪试验颗粒流宏细观分析[J]. 岩石力学与工程学报, 2012, 31(6): 1245–1256. ZHOU Yu, WU Shunchuan, ZHANG Xiaoping. Macro- and meso-analyses of rock joint direct shear test using particle flow theory[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(6): 1245–1256.
[18] 周喻, 吴顺川, 焦建津, 等. 基于 BP 神经网络的岩土体细观力学参数研究[J]. 岩土力学, 2011, 32(12): 3821–3826.ZHOU Yu, WU Shunchuan, JIAO Jianjin, et al. Research on mesomechanical parameters of rock and soil mass based on BP neural network[J]. Rock and Soil Mechanics, 2011, 32(12): 3821–3826.
[19] 吴顺川, 周喻, 高斌. 卸载岩爆试验及PFC3D数值模拟研究. 岩石力学与工程学报, 2010, 29(增2): 4082–4088.WU Shunchuan, ZHOU Yu, GAO Bin. Study of unloading tests of rockburst and PFC3D numerical simulation[J]. Journal of Rock Mechanics and Engineering, 2010, 29(Suppl 2): 4082-4088.
[20] 王莉, 谭卓英, 周喻, 等. 煤样巴西劈裂试验中声发射特性的细观模拟[J]. 北京科技大学学报, 2014, 36(3): 275–282. WANG Li, TAN Zhuoying, ZHOU Yu, et al. Mesoscopic simulation of the acoustic emission characteristic of coal samples in Brazilian test[J]. Journal of University of Science and Technology Beijing, 2014, 36(3): 275–282.
(编辑 罗金花)
flow code model and simulation of rock mass with negative Poisson’s ratio
JIN Aibing, WANG Kai, YANG Zhenwei, MENG Xinqiu
(School of Civil and Environment Engineering, University of Science and Technology Beijing, Beijing 100083, China)
In order to study the specific phenomenon of negative Poisson’s ratio of rock mass in the perspective of microstructure, a method of numerical simulation using particle flow theory and particle flow code (PFC) was proposed. An applicable PFC model of negative Poisson’s ratio of rock mass was constructed by studying the specific internal microstructure of inorganic crystals materials. A Poisson’s ratio curve of rock specimen was obtained in a numerical experiment of rock uniaxial compression using the PFC model. Based on the PFC model, the mechanism of negative Poisson’s ratio of rock specimen at low load level was interpreted. The results show that Poisson's ratio is negative when the axial compression is 0 to 3 MPa, and the minimum value is −0.059. The results of numerical simulation agree with the test data. The reliability of the PFC model used to study negative Poisson’s ratio of rock mass is verified.
rock mass; negative Poisson’s ratio; particle flow code(PFC); particle flow code model; microstructure
10.11817/j.issn.1672-7207.2015.09.035
TU45
A
1672−7207(2015)09−3422−07
2014−09−24;
2014−11−01
国家自然科学基金资助项目(51074014);中央高校基本科研业务费专项资金资助项目(FRF–SD–12–002A) (Project(51074014) supported by the National Natural Science Foundation of China; Project(FRF–SD–12–002A) supported by the Fundamental Research Funds for the Central Universities)
金爱兵,博士,副教授,从事岩土工程灾害治理研究;E-mail: jinaibing@ustb.edu.cn
