收入、房价与金融稳定性*——源自异质面板门槛模型的解析

沈 悦 郭培利



收入、房价与金融稳定性*——源自异质面板门槛模型的解析

沈 悦 郭培利

（西安交通大学经济与金融学院 陕西西安 710061）

本文以线性和非线性估计对比研究了不同收入的35个大中城市内房价对均衡值的偏离和房价的百分比波动分别作用于金融稳定性的效应。结果表明：无论房价偏离还是房价波动对金融稳定性的影响均显著存在收入门槛效应，前者为双门槛，后者为单门槛。不同门槛区间内房价与金融稳定性关系不同，中、低收入下支持价值偏离理论，高收入下支持价值抵押理论。房价偏离和房价波动的作用程度相差5倍以上。以房价偏离进行非线性估计被证明更科学。

收入 房价偏离 金融稳定性 非线性

一、引 言

房地产作为银行贷款的经常性抵押品，其价格波动对各国金融稳定的重要性毋庸置疑。世界多次金融危机均与房价波动关联：如2007年美国“次贷危机”、1999年日本泡沫经济崩溃、1997年东南亚金融危机以及我国海南房产泡沫等。关于房价与金融稳定性的研究在学术界一直是热议的焦点，且已形成一定理论。最近有学者如潘和王（Pan和Wang，2013）在研究二者作用时将收入的影响效应也考虑在内。收入水平影响着住房支付能力、国民财富增长等，与房价和金融稳定性的关系确实密切。细察我国经济现实，收入较高的一线城市北、上、广、深以及三线城市温州、神木等，房价波动剧烈，“跑路潮”等金融不稳定事件也发生频繁，收入中等和较低的城市内房价与金融稳定性变化就相对平和。由此本文推测收入水平会影响房价与金融稳定性的关系，不同收入水平下房价对金融稳定性的效应会不同。

关于房价与金融稳定性的关系，目前业界从金融加速器分析形成了两种对立的观点：一是价值抵押理论，认为房价上涨可以提升金融稳定性。房价上涨通过提高抵押资产价值推高了金融资本，由此降低借款者的违约可能性，减少金融资产的风险，从而提升了金融体系稳定性（Daglish，2009）。二是价值偏离理论，认为房价上涨会破坏金融稳定性。房价上涨将造成逆向选择和道德风险（Allen和Gale，2001），金融机构以不合理的低利率为客户提供大量贷款，房价预期也鼓励投资者借款，非理性繁荣下房价严重偏离均衡值，金融危机在经济或政策逆转时可能毫无征兆发生。那么，对于我国城市众多、财富差距较大的特殊国情，每个城市究竟该以哪一观点作为经济发展的指导？不同收入城市内房价与金融稳定性的关系具体如何？怎样才能更科学合理地对三者关系进行判定？基于以上考虑，本文试图解决以下问题：（1）我国房价对金融稳定性的影响是否存在收入的门槛效应；（2）若存在，那么高、中、低收入区间内房价与金融稳定性关系如何；（3）不同的房价变化测度标准对金融稳定性的影响是否存在差异。

二、文献综述

不少学者围绕房价和金融稳定性问题进行了理论探讨。申（Shin，2008）以房地产作为唯一资产模拟价格变动，发现资本金价值随价格变化而波动产生了风险，破坏了金融稳定性。古德哈特等（Goodhart et al.，2009）引入包含异质性的房产和银行，研究了抵押贷款、个人违约等如何将最初的房价冲击转化为金融不稳定。达格利什（Daglish，2009），帕里格若瓦和桑托斯（Paligorova和Stantos，2012）发现金融稳定性对房价变化高度敏感，尤其在房价下降时，若同时存在利率上升，则有极大可能导致部分客户无法偿还贷款，金融风险只能由银行自身承担。安德烈和阿尔塞（Andre和Arce，2012）模拟银行高度竞争化的特殊环境得出房价冲击的短期经济稳定效应比长期更强烈的结论。赫尔（Hull，2015）考虑如何稳定金融市场和降低不良贷款时开发出了一种可变更抵押贷款协议，通过绑定房价指数和主要债务实现。细查以上文献，在分析房价与金融稳定性的关系时所采用指标多为房价或其指数的百分比变化，近年已有学者认为应将房价对长期均衡值的偏离也考虑在内。斯捷潘尼扬等（Stepanyan et al.，2010）肯定了房价波动与多种金融因素关联后，就提出应加强房价对均衡值偏离的关注度，认为这是目前该研究领域的薄弱之处。克特尔和波格斯扬（Koetter和Poghosyan，2010）创新性展开了相关研究，分离出德国房价对均衡值的偏离，然后采用面板logit模型检验了房价变化对金融稳定性的价值抵押和偏离效应。潘和王（Pan和Wang，2013）也利用PMG估计分离了美国房价对均衡值的偏离，并同时采用房价百分比变化和房价偏离两个指标对比检验了银行不稳定性的响应状况。国内学者中仅邱崇明、李辉文（2011）率先使用了房价偏离测度，吸纳国际先进思想，在国内房价与银行稳定性研究中通过协整理论、probit估计发现我国房价上涨更倾向于在偏离回归效应下生成银行不稳定。由此可见，国内文献有关房价对均衡值偏离的研究几乎为凤毛麟角，同时采用多种房价指标进行金融稳定效应对比的文献更是暂时空白。

不过国内学者在房价与金融稳定性关系研究方面成果不少。如武康平等（2004）构建基于中国制度背景的一般均衡模型，揭示了过度繁荣环境下房价持续上涨将导致金融失衡的共生性关系。张晓晶、孙涛（2006）通过分析驱动房地产周期的增长面、宏观面与制度面因素得出房地产周期与金融稳定息息相关的结论。宋凌峰、叶永刚（2010）采用或有权益资产负债表方法发现过高和过低的房价都会增加房地产行业金融风险。谭政勋、王聪（2011）利用多元GARCH和动态随机一般均衡模型共同解释了房价、信贷及其联合波动作用于我国金融稳定性的经验机制。然而显然这些研究采用的均是线性方法，我国区域经济差距悬殊，变量之间很可能存在非线性关系。上文中潘和王（Pan和Wang，2013）的成果除了吸纳房价偏离思想外，最大贡献就是较之其他更进一步挖掘出房价与银行不稳定性之间存在收入增长影响下的非线性效应。早其几年的研究戈茨（Goetz，2009）也证实了资产价格对金融稳定性的影响在跨越门槛值前后存在明显的非线性结构突变。不过该研究在分类样本时通过强制划分资产价格下降程度进行，主观意念偏重。康和刘（Kang和Liu，2014）将中国内地和台湾的房价划分为不同层次，研究出台湾的高房价比内地在次贷危机中所受影响更深重，但也是采用外生性标准分类样本。搜集相关文献发现非线性结构解析近年才崭露头角，国内相关研究不多。徐晶（2013）对35个大中城市分析得出房价上涨的稳定效应有着阶段性的不同效果，在不同经济发展水平地区存在明显差异。赵杨等（2011）在时间维度区分了房价波动对居民消费、经济增长的阶段性效应，并结合收入进行了房地产财富效应的对比。但这些均为房价对宏观经济稳定的作用，具体至金融稳定性的非线性分析国内还未出现。高波等（2013）以动态GMM证实收入差距扩大是引发城市房价租金比升高的最主要因素。可见对中国房价与金融稳定性的分析纳入收入的非线性影响十分必要。

本文的创新之处在于：（1）以门限向量自回归（Threshold Vector Auto-regression, 又称“门槛模型”）获取的收入门槛值分类数据，从而进行房价与金融稳定性关系在异质样本间的非线性结构解析。此处取代了一般文献中强加外生性标准分离样本的方法，使得分析结果更加科学可靠。（2）采纳并构建了房价对均衡值的偏离指标（以下均简称为“房价偏离”）来分析房价与金融稳定性的关系，并同时使用房价的同比波动指标（以下均简称为“房价波动”）更深刻的进行对比挖掘，克服一般文献中单一角度论证欠周密的不足。

三、研究假设与模型设计

（一）假设提出

从理论上讲，收入、房价与金融稳定性三者之间相互关联。第一，房价变化与金融稳定性波动存在着千丝万缕的联系。金融机构的抵押、按揭贷款在房价变化时均因资产价值上升或下降而调整自身风险敞口或抵御能力；而房地产市场的荣衰则直接是资产价格波动下金融机构调整信贷利率和规模产生的结果。第二，金融稳定性与收入水平在风险投资、财富分配等作用下也相互制约。金融稳定与金融危机环境下投资者可获得的收入预期差别较大；高、低收入水平下资金投放的不同也直接影响着金融稳定性的强弱波动。第三，房价与收入之间因抵押资产价值、住房支付能力的牵连也存在着相互的影响。房价上涨必然增大居民的固定资产投资性收入，而收入上涨也会因提高了居民住房支付能力使整体房价水平被缓慢推升。因此，收入是房价与金融稳定性的重要连接纽带。

具体来看，收入较低时，居民财富大多用来消费，甚至无力支付房产，房价变化与此类群体关联不大，其金融稳定效应也较小。收入中等时，居民可累积部分财富用来购买或投资房产，房价变化紧密关联着此类群体的住房支付能力或投资预期收益，其金融稳定效应随着财富储蓄、信贷支持等的关联也相应增强，但此类群体收益及能力均有限，房价急速上涨或下跌时的非理性投资、违约偿贷等将会使金融稳定性遭受极大波动。收入较高时，财富分配在消费、投资、储蓄等渠道中选择余地大，是否投资或消费房产成为可选择性决策，因而带来的金融效应也具有不确定性，但不可置否地，对于此类群体而言投资至关重要，房地产又是偏好标的，所以此处房价变化对金融稳定性具有风向标的重要价值。综上可知，不同收入水平下房价变化对金融稳定性的影响必然不同。鉴于此，本文提出：

假设1：房价对金融稳定性的影响存在收入的门槛效应。

更进一步，中、低收入水平下，由于居民趋利性心理作用强烈，有限理性的局部思维方式很可能造成低概率风险的忽略，尤其对于房价上涨预期下成功示范效应带来的集体性行为，极大可能使得短期内风险迅速累积，使得金融稳定性遭受极大威胁，通常只有缓慢降低房价才能强制更改投资路径来逐步分散不良影响。高收入水平下，金融虚拟资产的利益诱惑已远超房产的缓慢收益，但选择前者也会使风险威胁出现乘数效应，因此大幅增加房产价值吸引投资从虚拟资产转向固定资产，才可平衡风险稳定整体金融系统。因而可看出，中、低收入水平时房价上涨偏向在偏离均衡值较大幅度时积累不易察觉的金融风险；高收入水平时房价上涨则偏向通过资产抵押价值的调整提升金融稳定性。鉴于此，本文提出：

假设2：中、低收入水平下房价对金融稳定性的影响支持价值偏离理论；高收入水平下房价对金融稳定性的影响支持价值抵押理论。

然而在研究房价和金融稳定性关系时常用的指标为房价波动，近年被证明效用良好且更加实用的房价偏离指标在国内研究中却非常罕见。房价波动的测度与基期数据选取的关联很强，在持续上涨时不会出现负数；而房价偏离却与区域综合经济相关，即使持续上涨也可能因低于均衡值而出现负向的反响修正。二者的描述统计会有较大区别，因此被推测对金融稳定性的影响也会存在较大差异。鉴于此，本文提出：

假设3：不同测度标准的房价偏离或房价波动对金融稳定性的影响也不相同。

（二）理论模型

关于房价偏离和房价波动对金融稳定性影响的分析，如何测度房价对均衡值的偏离是一难点，克特尔和波格斯扬（Koetter和Poghosyan，2010）针对德国78个地区提出过解决方案；而在同步考虑收入水平影响的条件下，另一需解决的关键就是怎样依据收入分离样本，潘和王（Pan和Wang，2013）使用美国286个大都市异质面板的收入、房价和银行数据做出过类似研究。综上，本文将模型设计如下：

首先，描述房价与其相关变量的长期关系。房价决定因素一般考虑住房需求与供给两个方面（史永东、陈日清，2009；Stepanyan et al.，2010），收入水平、人口密度、房价增长预期等都是主要的住房需求驱动；而由于区域分割、信息不对称等固有属性，房地产投资、土地短缺等也极大限制了住房供给。因此，本文将房价描述为：

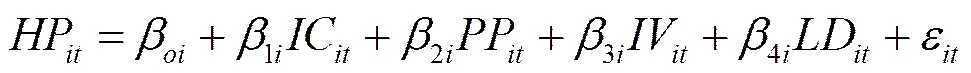
其中是35个大中城市的房地产价格；表示居民人均可支配收入；、、分别为人口密度、房地产投资、土地购置面积；为误差项；和分别表示城市和时间。、、的一阶滞后与房价存在着显著的协整关系，将式（1）整合为式（2）所示的一阶自回归分布滞后模型：

（2）

IV与IV­-1，LD与LD-1，以及IV­-1、LD-1与HP-1之间高度相关，多重共线性明显，所以不能直接利用式（2）回归。在房价滞后一期时，式（2）的误差修正形式为：

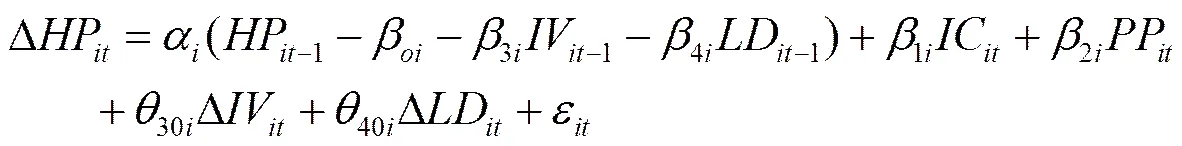
速度调整系数、截距项0i以及短期调整系数30i、40i随城市而变化，1i、2i、3i、4i为长期调整系数。其中预期为负，这就暗示房价对市场不均衡的反应有：随着长期正向偏离均衡值，房价下降；随着长期负向偏离均衡值，房价上升。对于式（2）和（3）的参数之间有如下关系：

（4）

通过估算可得误差修正项HPD-1= HP-1-- IC-1- PP-1- IV-1- LD-1，这一结果也就是房价对均衡值的偏离，并能够在下文分析中作为金融稳定性的一项决定因素。

其次，依据收入水平分离样本。收入水平被设定为与房价指标互动的门槛变量，利用汉森（Hansen，1999）提出的门限向量自回归模型取代一般文献中强加外部约束进行样本分离的方法，本文确定了收入门槛值，然后对我国35个大中城市10年间的面板数据进行了高、中、低收入城市的科学划分。关于门槛值的真实性和显著性需要进一步检验。相关步骤在实证分析中详述。

最后，根据分类后的异质性样本，在不同收入区间内分别估计房价偏离、房价波动对金融稳定性的影响。具体来讲，金融稳定性指标被作为房价偏离或房价波动、收入水平、相关金融因素等的一个因变量来进行估计，门槛模型设定为：

HPD-1是房价偏离的一期滞后估计结果；表示金融稳定性变量；代表相关金融变量和其他控制因素，为个体固定效应，e为误差项。在此背景下，根据门槛变量IC-1是大于还是小于门槛值将样本分类。如果回归斜率1和2不同，以房价波动变量为例，式（5）可写为：

（6）

其中，是表示收入区间的辅助函数。如果存在两个门槛值1和2，以房价偏离变量为例，式（5）可表示为：

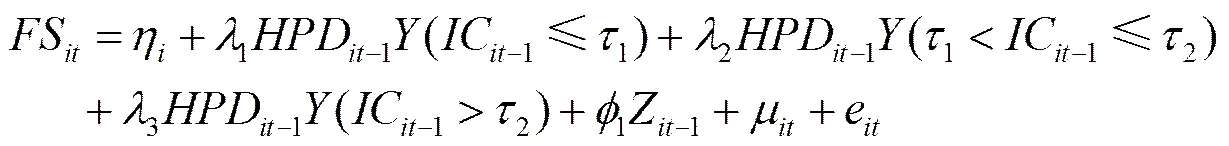
四、假设检验与实证分析

（一）变量选取及数据处理

本文将研究范围界定在收入差异具有一定代表性（如图1所示）且能将不可移动的房地产资产异质性考虑在内的35个大中城市区域。这些地区房价围绕我国整体均值有着相当的波动，房地产市场的城市间震荡差异较大。基于房价变化多取决于经济发展和人口增长的考虑以及已有文献关于住房需求、供给的理论分析，本文选定居民人均可支配收入、全市人口密度、房地产投资完成额、土地购置面积作为房价偏离测度的决定性因素。对于房价波动则以2003年为基期计算房价的百分比波动值。以上数据均来自《中国房地产统计年鉴》和《中宏产业数据库》。金融稳定性指标的选择关系重大，国外文献中不良贷款已成为一个常用变量（Kauko，2012），银行破产率（Cebula et al.，2011）、危机概率（Koetter和Poghosyan，2010）等也有被使用。然而我国区域金融对以上指标的采集或推算尚不完善，地区性金融统计数据中可获得的最相关变量即为《中国城市统计年鉴》中的金融机构各项存、贷款余额，翟光宇（2013）证明存贷比数据对流动性等金融风险的效应分析有效。因此，对本文来讲，金融机构存贷比在研究35个大中城市金融稳定性时即最适用变量。此外，根据房地产市场、金融稳定性波动来源和地区数据的可获得性，在设定门槛模型时国内生产总值、抵押贷款按揭贷款、财政收支比、工资增长额、消费增长额等被作为控制变量使用，数据均来自《中国城市统计年鉴》。鉴于所有可获得变量统计时间的一致性，本文选取2003-2012年为期限，表1展示了以上所有变量的描述性统计结果。为保证模型分析的稳定性，对数据进行了量纲差异消除及不平稳序列取差分或对数，房价同比波动转化为以2003年为基期的定基比数据等处理步骤。篇幅所限，不予陈述。

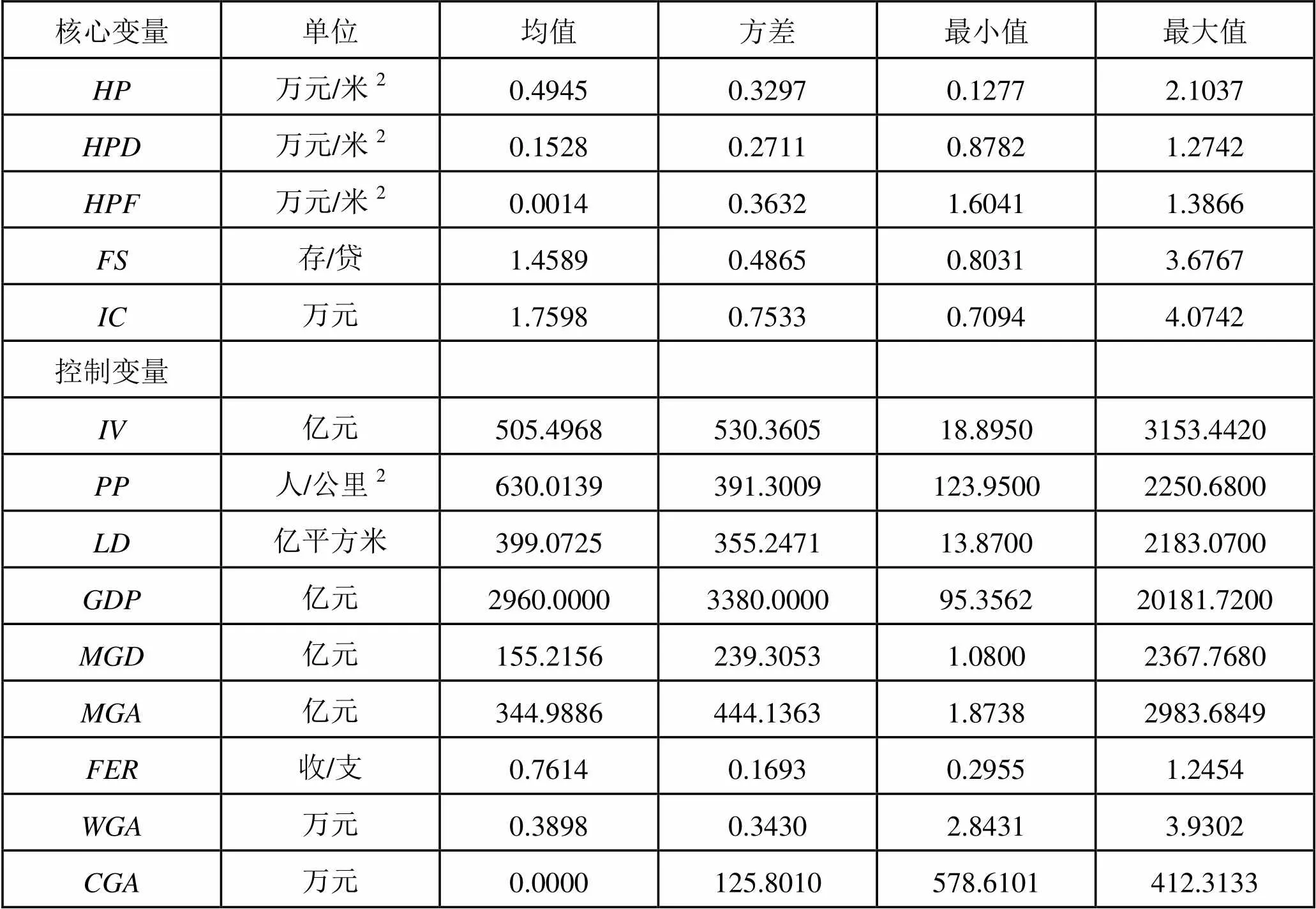
表1 35个大中城市相关变量的描述性统计量（2003-2012）

图1 35个大中城市收入水平层次图①图2 模型（A）第一门槛值检验

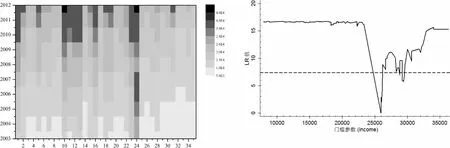
图3 模型（A）第二门槛值检验   图4 模型（B）单一门槛值检验

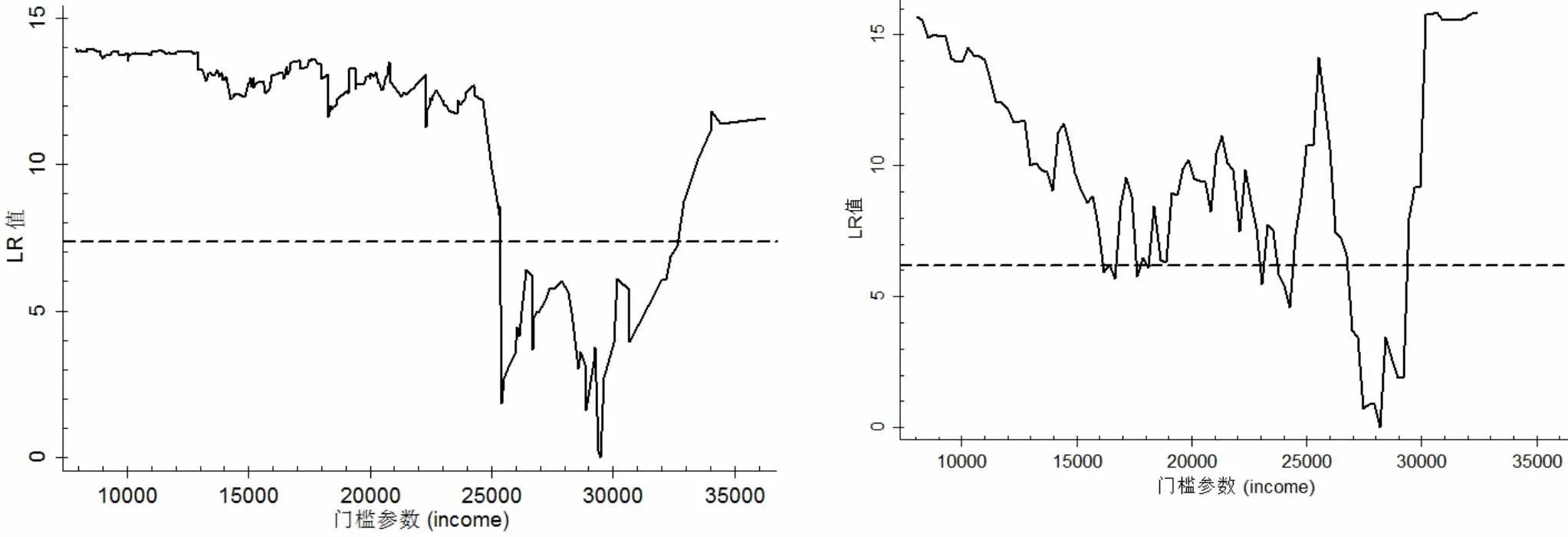
（二）房价偏离的测度

对于房价偏离的测度，由于式（2）和（3）随机误差项存在异方差和自相关，对比动态面板数据的估计方法后本文认为GMM（广义矩估计）更为有效，而且GMM为稳健估计，所得到的参数估计量比其他方法更合乎实际。表2列举了GMM得到的相关系数估计结果，根据式（4）的参数转换关系便可计算出的估计值房价偏离、房价波动以及原始房价的描述性统计量在表1中均已列示，其中和的均值正负不同，绝对值相差约1500，最小值的统计也差别甚大，由此可初步认定假设3的推测合理，采取房价偏离和房价波动两种指标对金融稳定性进行研究有着相当的意义和价值。

表2中P值的显著统计表明GMM方法的选择与使用是有效的。与预期和其他文献一致，在1%的水平上显著为-0.1860，表明我国上一年度房价对均衡值的偏离有18.60%在本年度被调整。根据相关文献方法，本文计算了房价在冲击下对长期均衡值调整的半衰期-（2）/（1+），得到了3.38年的结果，即在外部条件不变的情况下，我国房价从目前状态调整至均衡值需约3年半时间。克特尔和波格斯扬（Koetter和Poghosyan，2010），潘和王（Pan和Wang，2013）分别对德国、美国房价研究后得到的半衰期估计值为6.79年和2.75年。不同国家调整周期的不同应与当地房地产市场是否有效以及国家政策、经济环境相关。在此这一结果为我国房价向长期均衡值进行调整提供了参考。

表2 房价偏离测度的相关系数估计结果

注：***、**、*分别表示在1%、5%、10%水平下显著。

长期调整系数中房价的收入弹性1i不足0.10，这与潘和王（Pan和Wang，2013）对美国286个大都市房价收入弹性的估计值0.57差距较大，但与史永东、陈日清（2009）的研究结论比较一致。考虑到我国部分城市房价收入比甚至是美国数据的7、8倍，造成原因有统计口径、数据计算方法不同等，较为复杂，此处亦认为结果合理；房地产投资对房价的影响最强烈且为负的1.7640，据此分析我国房地产市场投资已接近饱和，继续增加只会加剧竞争而压低房价；其次人口密度增长对房价影响也相当明显，系数2i显示人口密度和房价几乎呈现同倍增长。短期调整系数30i对房价的作用也比较强烈，同样表明房地产投资对房价影响程度深重，但区别在于短期内投资效应为正，即会迅速推高房价，而在长期则导致竞争激烈迫使房价下降。综合这些估计结果，长期来看房地产投资、人口密度是推动我国房价上涨的重要因素；而短期内房地产投资是房价上涨的主要推力。人口密度增大造成的房价上涨很难调整，投资推动引起的房价上涨则相对容易改变。

（三）门槛值的获取与检验

遵从理论设计本文考虑了两种模型（A）和（B）。其中（A）为在门槛变量收入水平限制下房价偏离对金融稳定性的影响，对应式（6）；（B）为收入限制下房价波动对金融稳定性的影响，对应式（7）。在估计式（6）和（7）时，首先必须消除个体效应的影响，实证中可从每个观测值中减去组内平均值实现。然后进行是否存在收入门槛效应的非线性分析。从搜索一个门槛值开始，将门槛变量取值范围内的任一值作为初始值0赋给，以OLS估计方程得出对应的残差平方和（0）。再用同样的方法在区间内选取多个数值求得（），根据残差平方和最小化原则，使得（）最小的0就是可能的门槛值。对于多门槛模型基于同样的原理，直到第（+1）个门槛值不显著为止。估计出门槛值后，其他参数值也就能够相应确定。

接下来需检验门槛值的显著性和真实性。汉森（Hansen，1999）提供了F检验、极大似然估计等判断标准。对于单、双或三门槛模型方法均类似，限于篇幅，仅介绍单门槛模型检验方法。设定原假设和检验统计量为：

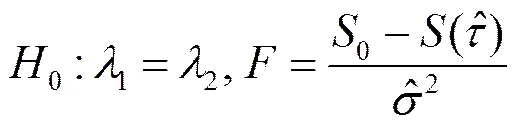
0表示不存在门槛效应，0为0条件下方程估计的残差平方和，且有0≥（）。为随机误差项方差的一致估计。在求得时的残差后可得：

（9）

若拒绝原假设0，则存在门槛效应。但因门槛值事先未定，F不服从2分布，故可使用“自抽样”（Bootstrap）模拟F的渐进分布来分析。本文利用Stata12.0软件得到如表3所示的F统计量，结果显示（A）应建立双门槛模型，（B）为单门槛模型。由此证明（A）和（B）均存在门槛效应，假设1的推测合理有效，即无论房价偏离还是房价波动对金融稳定性的影响均存在收入的门槛效应。

进一步需构造似然比统计量LR检验门槛值的真实性，汉森（Hansen，1999）认为当（）>-2（1-（1-）0.5）时门槛值真实（为显著性水平），其中：

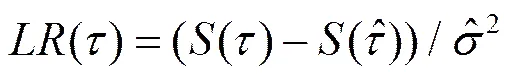
似然比统计量LR可作为门槛变量的函数进行绘制，如图2、3为模型（A）中检验第一、二门槛值时与LR的互动，图4是模型（B）的绘制结果。与零轴相交处即为模型的门槛值，虚线以下为95%置信区间，全部检验结果汇总至表4。可知房价偏离模型（A）的收入“分水岭”分别为25936元和29505元，房价波动模型（B）的“分水岭”为28205元，二者门槛效应不一致，再次证明假设3的推测合理有效。

表3 门槛效应检验结果

注：***、**、*分别表示在1%、5%、10%水平下显著。

表4 门槛值估计结果及置信区间

（四）门槛估计结果分析

通过以上门槛检验步骤，显著证明了房价对金融稳定性的影响存在收入门槛效应的假设1。根据内生性估计的门槛值，本文将模型（A）的样本划分为≤25936、25936＜≤29505、＞29505的高、中、低收入城市三类，将模型（B）的样本划分为≤28205、＞28205的高、低收入城市两类，进而分区间对模型参数估计。为了更加直观的分析模型结果，除门槛效应外，本文也采用面板固定效应模型对（A）、（B）估计，进行线性和非线性的结果对比。

表5 模型（A）和（B）的线性与非线性估计结果

注：***、**、*分别表示在1%、5%、10%水平下显著，括号内为t值。

如表5所示，第一，从面板固定效应模型的线性估计结果看，（A）中房价偏离和（B）中房价波动均在1%显著水平上对金融稳定性产生正向的强化作用，不同之处在于1单位正向的冲击影响为0.1963，而则远大于为0.9051。这一结果与业界房价上涨可以加强金融稳定性的学者观点互为佐证，尤其在影响程度方面也与部分文献近似。不难看出，这是由于模型（B）的指标计算和固定效应估计方法均与已有文献略同。的计算方法剔除了与基期相关的房价累积波动影响，因此仅为效应的46%。此处证明了假设3“不同房价变化测度方法对金融稳定性影响不同”推论的有效性，所得结论稳固，然而无法解释部分城市房价上涨却伴随频繁“跑路潮”的经济现实。

第二，从非线性门槛模型估计结果看，双门槛模型（A）中收入低于29505元的城市群和单门槛模型（B）中收入低于28205元的城市群房价上涨会破坏金融稳定性，高于这些收入标准的其他城市则在房价上涨时加强金融稳定性。具体来看，模型（A）的低收入水平下，1单位正向冲击对金融稳定性影响仅为-0.0929，比较微弱。这与低收入居民购房意愿不强，财富多用来消费，割裂了投资、储蓄的金融效应有关，负向的效应暗示了房价上涨加压居民支付能力的窘况，因此房价下降才能稳定金融市场。中等收入水平下，房价偏离对金融稳定性的作用在1%水平显著且影响较大，为-0.8526。该收入人群盈利欲望强烈而风险偏好不强，因此房产投资较多。当房价正向偏离时，上涨预期和信息不对称下低利率或低门槛的放贷和铤而走险的投资渠道异常开放，极易造成逆向选择的集体性行为，在政策或环境突变时将通过资金链断裂、信贷违约等流动性风险、道德风险使金融风险快速膨胀，强烈破坏金融稳定性。中、低收入水平下的分析均与价值偏离观点“房价上涨破坏金融稳定性”一致。高收入水平下，的系数显著为正向0.2996，与中、低收入水平下效应相反且仅约为其三分之一。富裕人群财富投资较多，金融虚拟资产收益较高且回笼较快，而房产收益不高却风险较小，因此只有房价大幅上涨才能吸引投资决策在最优选择中增大房产投资比重，使金融资本通过抵押资产价值上升的渠道而增值，进而降低信贷违约可能性，弱化金融风险，增强金融系统稳定。因此高收入水平下与的关系符合价值抵押观点“房价上涨提升金融稳定性”。模型（B）对和的分析与（A）总体一致，仅作用强度有异。低收入水平下影响为-0.6360，更接近在中等收入时的效应，这与门槛值28205和（A）的第二门槛值29505相差不大有关。高收入水平下对影响为2.8864，几乎是在高收入时效应的9倍，如此大的差异显著体现了一般文献中因指标计算导致的金融不稳定夸大。此处模型（A）和（B）同时证实了假设2关于“中、低收入水平下房价对金融稳定性的影响支持价值偏离理论；高收入水平下房价对金融稳定性的影响支持价值抵押理论”的论断，也再次验证了假设3。

第三，对比线性和非线性估计结果，模型（A）的线性固定效应估计更接近非线性双门槛模型中高收入区间估计结果；模型（B）的线性估计数值上与非线性模型低收入区间估计系数接近，方向却与高收入区间估计结果一致，可见模型（B）稳定性不如（A）。模型（A）和（B）的线性估计均过于粗糙，仅能说明和对作用的大致趋势。非线性门槛模型分区间细化了房价对金融稳定性的影响，可针对单一城市进行差别化指导，而且单、双门槛估计结果大约一致，相互论证，由此可知非线性门槛模型比线性固定效应分析可靠性更强。此外，无论模型（A）还是（B），也无论线性还是非线性估计，所有控制变量的系数均正负一致且大小相差不多，由此可知文中选取这些变量来缩小模型误差达到了预期效果。综合以上分析，可知房价偏离模型（A）的非线性门槛估计结果稳定性和可靠性最佳。

五、结 论

本文通过理论分析发现收入不仅对城市房价、金融稳定性都存在着直接影响，作为关联纽带也间接作用于二者关系，因而采用我国35个大中城市2003至2012年的异质面板数据构造了线性固定效应和非线性门槛模型，将房价对金融稳定性的影响在不同收入城市中进行了实证检验。具体得到如下结论：（1）房价对金融稳定性的影响存在收入的门槛效应，且从房价对均衡值的偏离分析存在双门槛值，从房价的同比波动分析存在单一门槛值。（2）无论房价偏离还是房价波动，在中、低收入水平下均支持“房价上涨破坏金融稳定性”的价值偏离理论；跨越门槛值进入高收入水平后则支持“房价上涨提升金融稳定性”的价值抵押理论。（3）不同测度方法的房价偏离和房价波动对金融稳定性作用程度差异较大，后者约为前者的5至9倍。（4）收入水平、人口密度是驱动我国房价偏离的重要因素，在当前环境下房价调整至均衡值需用时约3.38年。（5）非线性门槛模型下房价偏离对金融稳定性的影响效应被证明相对最稳定和可靠。

为此，本文提出以下政策建议：

第一，把握时机适当提高高端住宅、投资型住房、改善性住房销售价格；尽可能调整刚需型住宅价格回归均衡值，拉开与前者的支付差距。高收入群体对房产的偏好在于投资和改善性居住，主要关注房价预期波动如何，对房价均衡值不甚敏感；又因固定资产投资相较金融虚拟资产风险小，因此一定程度提高此类房产价格既可吸引高收入群体投资，又可稳定金融市场平衡，达到共赢互利的效果。对于刚性需求购房者，迫切需要质量可靠、价格低廉的紧凑型房屋，若此类房价也长期高于均衡值就只能望房兴叹。刚需群体占据着我国相当比例，基础层次需求的长期不得满足不仅对金融市场甚至社会发展都将造成严重后果。

第二，以调整房价来稳定区域金融市场时应综合考虑当地收入水平、人口密度等状况，否则可能适得其反。我国幅员辽阔，城市之间经济发展差距较大，一味地认为打压房价便可利国利民的口号不可取，“一刀切”管理模式完全不符合我国宏观调控。具体来讲，收入较高的城市群如北、上、广、深等适合有控制和规划地部分提升别墅、高档小区等房价增幅；而大部分中、低收入城市则应依据居民住房支付能力和房地产市场供求来稳定当地房屋销售价格，而非全国性跟风房价变化。

第三，在数据信息、技术能力支持的条件下，采用更加科学可靠的测度和评估方法衡量我国房价变化、金融监管、收入差距等经济状况，可产生更为合理有效、针对性强的政策指导。目前我国政府评估采用的方法手段与社会技术更新步调不很一致，信息统计和披露程度也较国际相对保守。区域金融市场不良资产、总贷款负债比等国际公开数据在我国搜集仍较为困难；非线性门槛估计等国际广泛应用模型在我国使用仍较为有限。21世纪科技日新月异，虽然我国整体庞大，但仍然必须杜绝尾大不掉的弊端，为了国计民生，及时学习和应用时新技术，提升业务质量。

最后，虽然本文得出了一些有益的结论，但鉴于国内城市金融数据的可获得性，仅选取了35个大中城市的10年数据为样本，且变量确定方面受到一定限制，所以在双门槛模型的低收入城市中所得结论不甚显著。随着我国信息披露强度扩大，未来以更多城市的相关数据研究收入限制下房价对金融稳定性的影响将有更具体和重大的指导价值。

1. 高波、王文莉、李祥：《预期、收入差距与中国城市房价租金“剪刀差”之谜》[J]，《经济研究》2013年第6期。

2. 邱崇明、李辉文：《房价波动、银行不稳定和货币政策》[J]，《财贸经济》2011年第3期。

3. 宋凌峰、叶永刚：《中国房地产行业宏观金融风险研究——基于金融稳定的视角》[J]，《经济管理》2010年第12期。

4. 史永东、陈日清：《不确定性条件下的房地产价格决定：随机模型和经验分析》[J]，《经济学（季刊）》2009年第1期。

5. 谭政勋、王聪：《中国信贷扩张、房价波动的金融稳定效应研究——动态随机一般均衡模型视角》[J]，《金融研究》2011年第8期。

6. 武康平、皮舜、鲁桂华：《中国房地产市场与金融市场共生性的一般均衡分析》[J]，《数量经济技术经济研究》2004年第10期。

7. 徐晶：《房价上涨与经济增长的退耦分析》[J]，《管理世界》2013年第9期。

8. 翟光宇：《存贷比监管指标是否应该放松——基于中国上市银行2007—2012年的季度数据分析》[J]，《经济理论与经济管理》2013年第6期。

9. 张晓晶、孙涛：《中国房地产周期与金融稳定》[J]，《经济研究》2006年第1期。

10. 赵杨、张屹山、赵文胜：《房地产市场与居民消费、经济增长之间的关系研究——基于1994-2011年房地产市场财富效应的实证分析》[J]，《经济科学》2011年第6期。

11. Allen, F. and Gale, D., 2001, Comparing Financial Systems [M], MIT Press, Cambridge, PP155-160.

12. Andre, S. J. and Arce, O., 2012, “Banking Competition, Housing Prices and Macroeconomic Stability” [J],, Vol.122, PP1346-1372.

13. Cebula, R., Koch, J. and Fenili, R., 2011, “The Bank Failure Rate, Economic Conditions and Banking Statutes in the U.S.” [J],, Vol.39(1), PP39-46.

14. Daglish, T., 2009, “What Motivates a Subprime Borrower to Default?” [J],, Vol.33, PP681-693.

15. Goetz, V. P., 2009, “Asset Price and Banking Distress: A Macroeconomic Approach” [J],, Vol.5, PP298-319.

16. Goodhart, C. A. E., Tsomocos, D. P. and Vardoulakis, A. P., 2009, “Modeling a Housing and Mortgage Crisis” [R], Central Bank of Chile Working Paper, No.547.

17. Hansen, B.E., 1999, “Threshold Effects in Non-dynamic Panels: Estimation, Testing and Inference” [J],, Vol.93, PP345-368.

18. Hull, I., 2015, “The Macro-financial Implications of House Price-indexed Mortgage Contracts” [J],, Vol.127, PP81-85.

19. Kang, H. H. and Liu, S. B., 2014, “The Impact of the 2008 Financial Crisis on Housing Prices in China and Taiwan: A Quantile Regression Analysis” [J],, Vol.42, PP356-362.

20. Kauko, K., 2012, “External Deficits and Non-performing Loans in the Recent Financial Crisis” [J],, Vol.115, PP196-199.

21. Koetter, M. and Poghosyan, T., 2010, “Real Estate Prices and Bank Stability” [J],, Vol.34, PP1129-1138.

22. Paligorova, T. and Stantos, J. C., 2012, “Monetary Policy and Bank Risk-Taking: Evidence from the Corporate Loan Market”[J],, Vol.7, PP1-57.

23. Pan, H. R. and Wang, C., 2013, “House Prices, Bank Instability and Economic Growth: Evidence from the Threshold Model” [J],, Vol.37, PP1720-1732.

24. Shin, H. S., 2008, “Risk and Liquidity in a System Context” [J],, Vol.17(7), PP315-329.

25. Stepanyan, V., Poghosyan, T. and Bibolov A., 2010, “House Price Determinants in Selected Countries of the Former Soviet Union” [R], IMF Working Paper.

（YH）

① 35个大中城市：1北京，2天津，3石家庄，4太原，5呼和浩特，6沈阳，7大连，8长春，9哈尔滨，10上海，11南京，12杭州，13宁波，14合肥，15福州，16厦门，17南昌，18济南，19青岛，20郑州，21武汉，22长沙，23广州，24深圳，25南宁，26海口，27重庆，28成都，29贵阳，30昆明，31西安，32兰州，33西宁，34银川，35乌鲁木齐。

*本文得到国家自然科学基金项目（71373201）和西安交通大学重大重点招标项目（skz2014003）的资助。