薄壁箱梁的弯曲纵向位移函数与剪力流

李丽园，周茂定，张元海



薄壁箱梁的弯曲纵向位移函数与剪力流

李丽园，周茂定，张元海

(兰州交通大学土木工程学院，甘肃兰州，730070)

以薄壁箱梁的弯曲理论为基础，从分析微板剪力流出发，结合弹性理论中求解平面应力问题的假设，推导考虑薄壁箱梁各板面内剪切效应时的弯曲纵向位移函数，同时从理论上导出剪力滞翘曲位移函数。运用能量变分原理及铁木辛柯深梁理论的假设简化并求解考虑各板面内剪切效应的纵向位移函数，并给出数值算例。研究结果表明：按本文推导的考虑各板面内剪切效应的位移函数计算的简支梁跨中截面正应力与实测值及有限元值吻合良好，剪应力与挠度较以往方式求解的结果更为准确，且箱梁挠度及腹板剪应力计算值相对于初等梁的结果均有明显增加，最大增量达到21%。

薄壁箱梁；面内剪切效应；能量变分法；挠度；剪力流

在现代桥梁建设中，薄壁箱梁有着重要的应用，对其弯曲力学性能研究的文献已有很多[1−4]。众所周知，在弯曲荷载作用下，薄壁箱梁由于各翼板剪切效应的影响，其纵向位移模式不再符合平截面假定，从而产生剪力滞效应，国内外许多学者已对此做了大量研究。 Reissner[5]首先引入能量变分法求解无翼缘板矩形薄壁箱梁的剪力滞效应，后来能量变分法被国内外学者应用于带悬臂板箱梁的剪力滞效应分析。对于剪力滞翘曲位移函数的形式，不同学者的假设也各不相同，有抛物线[4−7]、余弦函数[2]及悬链线[8]等多种形式。对于不同宽度翼缘板的剪力滞翘曲位移函数的修正方式，各学者也是观点各异[2, 9−13]。对于薄壁箱梁腹板剪切效应的研究，一直沿用铁木辛柯深梁理论[14]。然而，已有文献中将薄壁箱梁腹板和翼板的面内剪切变形分别提出不同的概念来分析，不便于理解，且只分析各板剪切效应对翼板正应力和箱梁挠度的影响，几乎没有文献研究各板剪切效应对薄壁箱梁剪应力的影响，对于剪力滞翘曲位移函数仍采取人为假定方法，缺乏理论证实。本文作者将在已有文献的基础上，通过对薄壁箱梁微元的分析，结合弹性理论中平面应力问题假设及铁木辛柯的深梁理论，推导出系统考虑薄壁箱梁各板面内剪切变形的弯曲纵向位移函数，并通过算例及ANSYS有限元对比分析，得出按此位移函数计算的正应力、剪应力和挠度的计算精度有较大 提高。

1 考虑面内剪切效应的位移函数

图1所示为薄壁箱梁在任意竖向分布荷载()作用下的受力简图。图中采用正交笛卡儿坐标系，坐标原点位于截面形心处。

(a) 坐标系及荷载；(b) 横截面

任取上述薄壁箱梁微板d×d如图2所示,为壁厚，为沿梁周边的横向坐标，σ为纵向正应力，为板面内剪切剪力流。

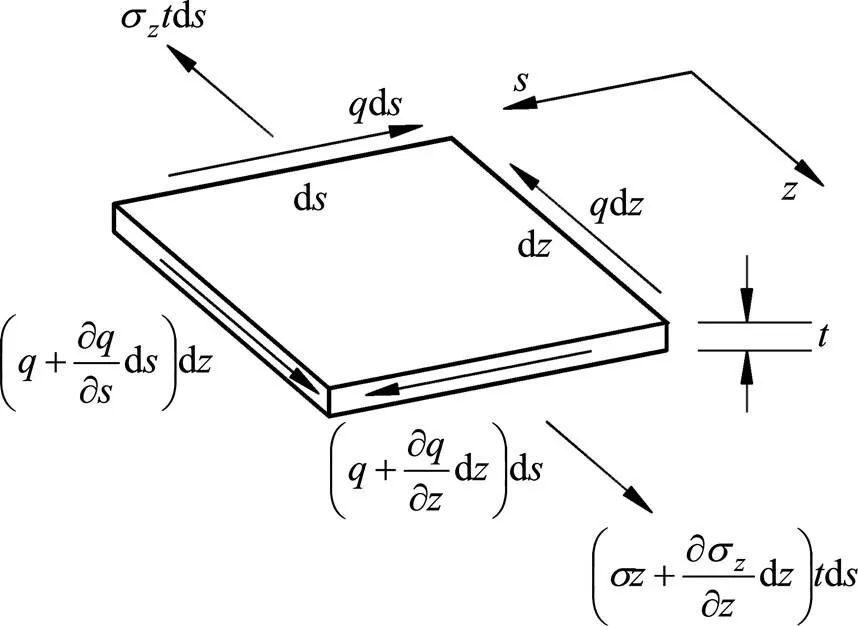
图2 薄壁单元中剪力流

根据力沿轴方向平衡条件可得微分关系式[13]：

对于微元薄板，若忽略面外的拉伸(或压缩)则转化为弹性力学中的平面应力问题，因而可得其位移与应变关系如下[16−17]：

式中：为纵向位移；为横向位移。

对图1所示的关于轴对称的薄壁箱梁截面，在弯曲荷载作用下，通常忽略截面沿周边的挤压变形，即认为ε=0；而在初等梁理论下，忽略各板的面内剪切变形，即认为=0，按此假设将会影响求解精度，因而需考虑薄壁箱梁各板面内剪切变形的影响。按上述假设下，薄壁箱梁的弯曲正应力σ计算公式如下[18−19]：

将式(5)代入式(1)结合弯矩与剪力的关系以及薄壁箱梁的弯曲理论[3,13]可得图1所示截面弯曲剪力流的一般计算公式为

式中：0()为相应开口截面剪力流。若将图1截面的开口选在顶板中心0点处时，式(6)等号右边第2项为0，因而其剪力流计算式如下(逆时针为正)：

现以顶板为例进行分析，其弯曲剪力流为

式中：y为箱梁截面水平形心轴至顶板中面的距离。仍忽略顶板沿周线的位移()，由式(4)可得：

式中：为剪切弹性模量。对式(9)积分整理后可得：

式中：0()为顶板中心(坐标起始点)的纵向位移，式(10)为考虑顶板面内剪切变形后箱梁顶板纵向位移沿横向的表达式。由式(10)可得，箱梁顶板与腹板交界处1点的纵向位移为

若令

并采用坐标表示顶板任一点横向位置，则式(10)可转换为

同样，对底板积分起点取截面左右对称中心点2处，对悬臂板积分起点取悬臂边缘3点处，可得底板和悬臂板的纵向位移分别为

此时薄壁箱梁截面的各翼板的纵向位移可用1()和4()表示。

从图3可以看出：腹板剪力流分布为二次函数，若设5点处剪力流为5()，则腹板任意一点剪力流为

式中：为腹板中线与轴的夹角。由式(15)及式(4)可得：

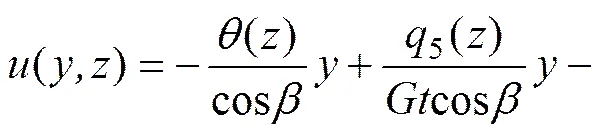
式(17)可表示箱梁截面腹板任意一点纵向位移函数。由式(17)可求得1()和4()表示如下：

若令

；

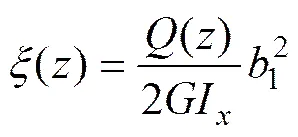
此时箱梁截面的各板元纵向位移可表示为

若求得5点处的纵向位移则可求得薄壁箱梁考虑各板面内剪切效应时的弯曲位移函数。

在材料力学中计算梁的弯曲内力时，通常将梁简化为截面中性轴处的一条线，因而腹板上也必然存在纵向位移为零的中性点[18]。对薄壁箱梁在不考虑各板面内剪切效应时，形心轴与中性轴重合，若考虑了剪切效应时，会导致中性轴与形心轴发生偏离。

当箱梁发生竖向挠曲时，由胡克定律和式(2)可知，截面上一点的正应力(,,)可表示为

对于不受轴力的受弯梁而言，箱梁横截面上应力总和应为零[15]，即：

结合式(20)~(22)可得：

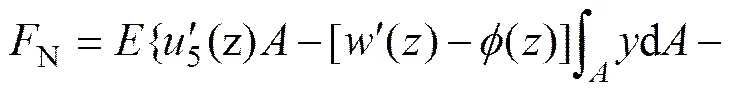
式中：

称式(24)为剪力滞翘曲位移函数。分析式(23)，由截面对称性可知，大括号内第2项和第3项为0，若令第4项积分后的结果为×(z)，其中

式中：A，A和A分别为箱梁顶板、两侧悬臂板、底板的截面积，则由式(23)和(25)可得：

式中：为截面面积，=−。从式(26)可知：5()为形心轴处相对于实际中性轴(纵向位移为零处)的纵向位移，具体可参见图4。

(a) 横截面；(b) 侧立面(纵向位移分布)

图4 翘曲位移函数及纵向位移简图

Fig. 4 Sketch map of warping displacement function and longitudinal displacement

由式(20)，(24)和(26)可得修正后薄壁箱梁剪力滞翘曲位移函数：

至此，便推导完成了薄壁箱梁考虑各板面内剪切变形后弯曲纵向位移函数。

2 能量变分法求解

由于涉及未知参数较多，对于各板考虑面内剪切变形位移函数的求解将十分困难。为了简化分析，可根据铁木辛柯深梁理论的假设，针对本文研究的薄壁箱梁即假设腹板有一均匀的剪切变形，亦即箱梁全截面有一转角()，忽略()项对腹板剪切的影响。按上述假设则式(20)的位移函数中()将为0，若令()=()−()时，则箱梁截面的纵向位移可表示为

(,,)=−(z)+ω(,)() (28)

薄壁箱梁正应变能e为

各翼板剪切变形剪应变能π为

腹板剪切变形引起全截面的应变能π为

式中：A为翼板面积；为不均匀剪切修正系数。

外荷载势能π为[12]

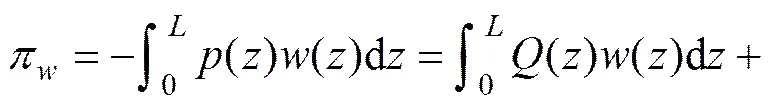
总势能为：

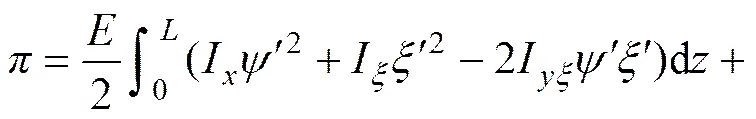
根据最小势能原理的驻值条件，可知δ0，对式(33)进行变分并整理简化后可得：

由上述基本方程式(34)~(36)消去和后，可得关于的微分方程为

在考虑腹板剪切变形能量后，并不影响翼板剪力滞翘曲位移函数的微分形式。

通过式(37)和(38)可得边界条件为

当通过式(39)解出()后，由式(34)和(35)即可积分计算()和()。()表达式为

式中：*()为求解()时与荷载有关的特解。

根据实际边界条件及荷载形式，求得()和()后，代入式(21)便可求得相应正应力(,,)。

通过求出的考虑各板面内剪切变形后的正应力(,,)，代入式(1)后，两边关于积分后可得：

式中：q()为积分起点处的剪力流，其可根据薄壁箱梁弯曲理论计算剪力流时的变形协调条件来求得。从而可求得薄壁箱梁考虑各板面内剪切变形后的剪 力流。

3 数值算例

3.1 简支梁正应力

有机玻璃制作的简支箱梁模型的横截面如图5所示[4]，在跨中截面梁顶腹板位置作用对称集中荷载，总值为=272.2 N。计算跨度=800 mm，材料弹性模量为3 000 MPa，泊松比为0.385。

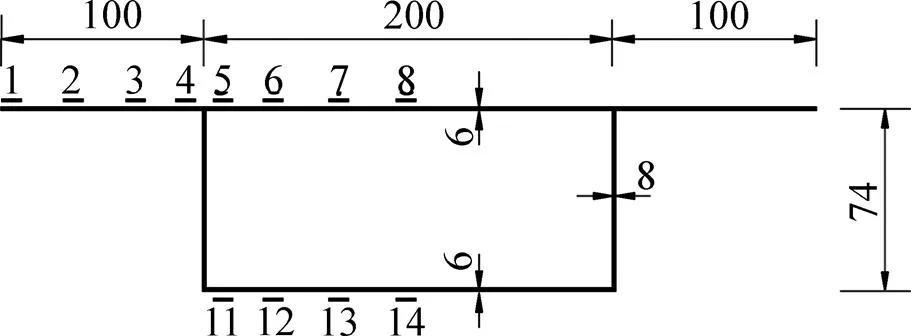
单位：mm

按照本文建立的薄壁箱梁弯曲纵向位移函数求得跨中截面应力连同文献[4]提供的实测值和空间有限元计算值列于表1中，以便比较。

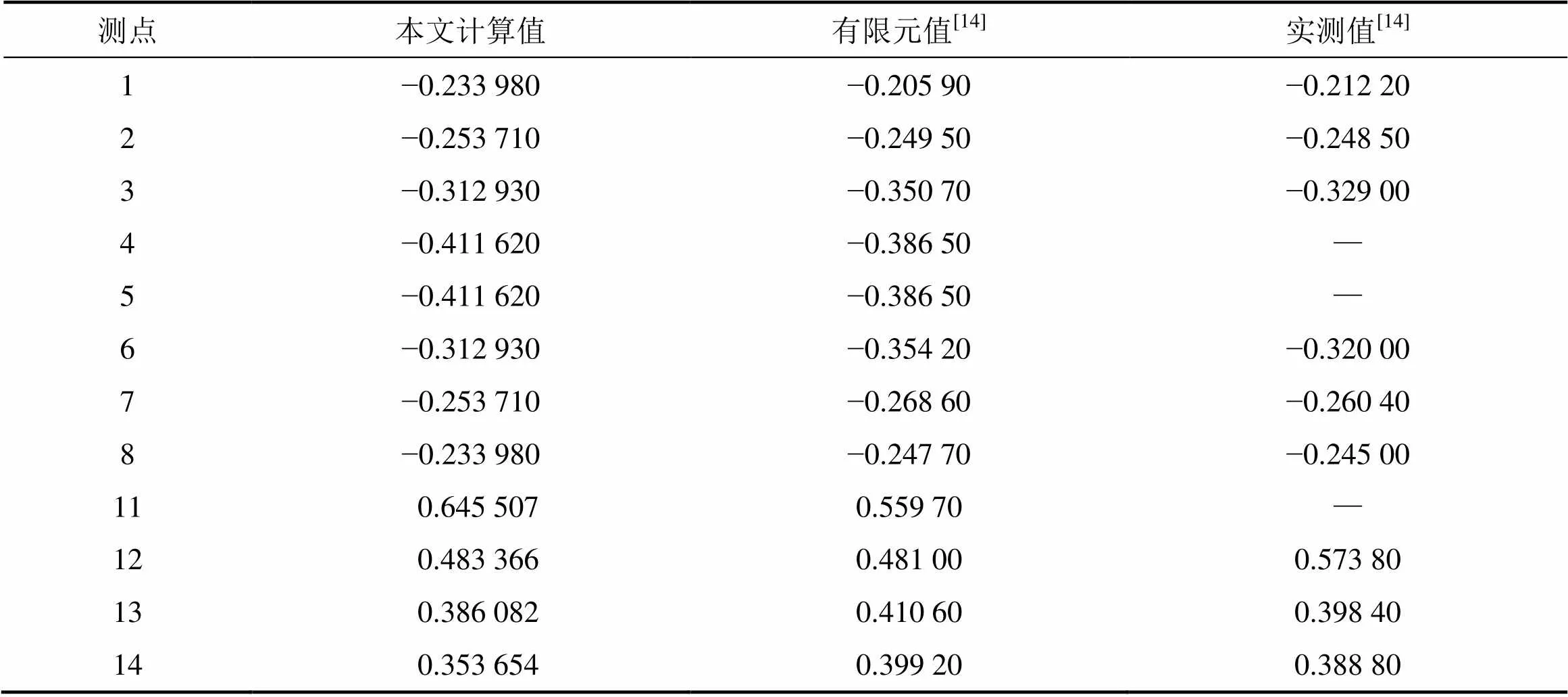
表1 简支箱梁模型跨中截面应力

通过表中计算值与有限元和实测值的对比可知：本文计算值与有限元及实测值吻合良好，少数值的偏差是应力集中引起，说明本文推导的位移函数合理。

3.2 简支梁挠度及剪应力

从前面的理论分析可知：当考虑各板的面内剪切变形后，薄壁箱梁的挠度和弯曲剪力流将会改变，为了说明此情况，仍以3.1节中的算例模型为例分析。

运用ANSYS中的shell63单元建立空间有限元模型[20−21]，共划分为1 158个节点和1 520单元，跨中集中荷载施加于腹板与顶板交界点，约束两端底板竖向位移及一端的纵向、横向位移。分别计算考虑和不考虑薄壁箱梁各板面内剪切变形的挠度和截面的弯曲剪应力，并将结果与ANSYS计算值对比。

为方便表示，现定义相对位置参数和如下。

对于顶板：1；对于悬臂板：3+1；

对于底板：2；对于腹板：/；纵向位置：。

3.2.1 挠度对比分析

考虑和不考虑薄壁箱梁各板面内剪切变形时跨中最大挠度分别为0.235 mm和0.192 mm，而ANSYS计算值为0.249 mm，考虑面内剪切效应后挠度计算值与ANSYS接近，较不考剪切效应时精度可提高22%，全部挠度结果对比如图6所示。

1—不考虑剪切效应；2—考虑剪切效应；3—ANSYS计算

3.2.2 剪应力对比

为了减小应力集中影响，取0.45处截面上、下翼板及腹板剪应力进行对比；为研究顺桥向变化趋势，取底板=0.8处各点剪应力进行对比，结果如图7所示。

(a) 上翼板；(b) 下翼板；(c) 腹板；(d) 底板χ为0.8处

从图7可知：考虑各板面内剪切效应时的剪应力计算值与ANSYS分析值吻合良好；各板弯曲剪应力值与以往文献不考虑剪切效应时[1,3]求得的值有较大差异，上、下翼板剪应力有大幅减小，且不再为直线形，腹板最大弯曲剪应力有大幅增加，此问题在薄壁箱梁设计时，应予以重视；对比底板=0.8处沿梁纵向变化趋势可知，在跨中集中荷载附近剪应力与传统方法求解值相差较大(支点处的约束导致ANSYS计算值出现差异)，说明薄壁箱梁各板的剪切效应不仅引起正应力的改变，也使剪应力有较大变化。

4 结论

1) 从薄壁箱梁微元板的分析出发，结合弹性力学平面应力问题的假设，推导了考虑薄壁箱梁各板面内剪切效应时的弯曲位移函数，并引入铁木辛柯深梁理论的假设对考虑各板面内剪切效应的位移函数进行简化，结合能量变分原理对其进行求解。

2) 按照建立的考虑薄壁箱梁各板剪切效应的位移函数求得的正应力值与实测值和有限元值吻合良好。考虑剪切效应时剪应力及挠度与ANSYS结果吻合较好；与不考虑剪切效应时的计算值相比，薄壁箱梁上(下)翼板处剪应力值有大幅度减小，而挠度和腹板剪应力有大幅度增加，最大增量可达21%，因而薄壁箱梁设计时应予以重视。

[1] 郭金琼, 房贞政, 郑振. 箱形梁设计理论[M]. 2版. 北京: 人民交通出版社, 2008: 1−50. GUO Jinqiong, FANG Zhenzheng, ZHENG Zhen. Design theory of box girder[M]. 2nd ed. Beijing: China Communications Press, 2008: 1−50.

[2] 倪元增, 钱寅泉. 弹性薄壁梁桥分析[M]. 北京: 人民交通出版社, 2000: 90−98. NI Yuanzeng, QIAN Yinquan. Elastic analysis of thin-walled beam bridges[M]. Beijing: China Communications Press, 2000: 90−98.

[3] 包世华, 周坚. 薄壁杆件结构力学[M]. 北京: 中国建筑工业出版社, 2005: 1−20. BAO Shihua, ZHOU Jian. Structural mechanics of thin-walled bar[M]. Beijing: China Building Industry Press, 2005: 1−20.

[4] 张士铎, 邓小华, 王文州. 箱形薄壁梁剪力滞效应[M]. 北京: 人民交通出版社, 1998: 111−132. ZHANG Shiduo, DENG Xiaohua, WANG Wenzhou. Shear lag effect in box girders[M]. Beijing: China Communications Press, 1998: 111−132.

[5] Reissner E. Analysis of shear lag in box beams by the principle of the minimum potential energy[J]. Quarterly of Applied Mathematics, 1946, 4(3): 268−278.

[6] 韦成龙, 曾庆元, 刘晓燕. 薄壁箱梁剪力滞分析的多参数翘曲位移函数及其有限元法[J]. 铁道学报, 2000, 22(5): 60−64. WEI Chenglong, ZENG Qingyuan, LIU Xiaoyan. Warping displacement function and finite element method for calculation of shear lag effect in box girder[J]. Journal of the China Railway Society, 2000, 22(5): 60−64.

[7] 吴幼明, 罗旗帜, 岳珠峰. 薄壁箱梁剪力滞效应的能量变分法[J]. 工程力学, 2003,20(4): 161−165. WU Youming, LUO Qizhi, YUE Zhufeng. Energy-variational method of the shear lag effect in thin walled box girders[J]. Engineering Mechanics, 2003, 20(4): 161−165.

[8] 甘亚南, 周广春. 薄壁箱梁纵向剪滞翘曲函数精度选择的研究[J]. 工程力学, 2008, 25(6): 100−106. GAN Yanan, ZHOU Guangchun. An approach for precision selection of longitudinal shear lag warping displacement function of thin-walled box girders[J]. Engineering Mechanics, 2008, 25(6): 100−106.

[9] 张元海, 白昕, 林丽霞. 箱形梁剪力滞效应的改进分析方法研究[J]. 土木工程学报, 2012, 45(11): 153−158. ZHANG Yuanhai, BAI Xin, LIN Lixia. An improved approach for analyzing shear lag effect of box girders[J]. China Civil Engineering Journal, 2012, 45(11): 153−158.

[10] 蔺鹏臻, 刘凤奎, 杨军, 等. 箱梁剪滞翘曲位移函数的定义及其应用[J]. 计算力学学报, 2012, 29(5): 789−794. LIN Pengzhen, LIU Fengkui, YANG Jun, et al. Definition and application of shear-lag warping displacement functions for box girders[J]. Chinese Journal of Computational Mechanics, 2012, 29(5): 789−794.

[11] 甘亚南, 周广春, 赫中营. 曲线梯形箱梁静力分析的多参数翘曲位移函数法[J]. 铁道学报, 2011, 33(7): 104−109. GAN Yanan, ZHOU Guangchun, HE Zhongying. An proach to multi-parameter warping displacement function for static analysis of curved trapezoidal thin-walled box girders[J]. Journal of the China Railway Society, 2011, 33(7): 104−109.

[12] 周茂定, 李丽园, 张元海. 薄壁箱梁的剪力滞翘曲位移函数研究[J]. 中国公路学报, 2015, 28(6): 67−73. ZHOU Maoding, LI Liyuan, ZHANG Yuanhai. Research on shear-lag warping displacement function of thin-walled box girders[J]. China Journal of Highway and Transport, 2015, 28(6): 67−73.

[13] 周茂定, 李丽园, 张元海.弹性常数在薄壁箱梁剪力滞分析中的影响[J]. 公路, 2015, 60(6): 57−60. ZHOU Maoding, LI Liyuan, ZHANG Yuanhai. Influence of constant in the shear lag analysis of thin-walled box girders[J]. Highway, 2015, 60(6): 57−60.

[14] 张元海. 箱形梁桥剪力滞效应及温度效应理论研究及其应用[D] . 成都: 西南交通大学土木工程学院, 2008: 66−70. ZHANG Yuanhai. Theoretocal study and application of shear-lag and temperature effect in box-girder bridges[D]. Chengdu: Southwest Jiaotong University. School of Civil Engineering, 2008: 66−70.

[15] 黄剑源. 薄壁结构的扭转分析(上册)[M]. 北京: 中国铁道出版社, 1983: 1−37. HUANG Jianyuan. Torsional analysis of thin-walled structures (Part one)[M]. Beijing: China Railway Publishing House, 1983: 1−37.

[16] 徐芝纶. 弹性力学(上册)[M]. 北京: 高等教育出版社, 2006: 9−-45. XU Zhilun. Elasticity mechanics (Part one)[M]. Beijing: Higher Education Press, 2006: 9−45.

[17] Timoshenko, Goodier. 弹性理论[M]. 第3版. 徐芝纶, 译. 北京: 高等教育出版社, 2013: 1−50. Timoshenko, Goodier. Theory of elasticity[M]. 3rd ed. XU Zhilun, transl. Beijing: Higher Education Press, 2013: 1−50.

[18] 孙训方, 方孝淑, 关来泰. 材料力学(上册)[M]. 北京: 高等教育出版社, 2002: 90−155. SUN Xunfang, FANG Xiaoshu, GUAN Laitai. Material mechanics (Part one)[M]. Beijing: Higher Education Press, 2002: 90−155.

[19] 吴亚平, 程耀芳, 康希良. 工程力学简明教程[M]. 北京: 化学工业出版社, 2005: 121−126. WU Yaping, CHENG Yaofang, KANG Xiliang. The introductory tutorial on engineering mechanics[M]. Beijing: Chemical Industry Press, 2005: 121−126.

[20] 吴鸿庆, 任侠. 结构有限元分析[M]. 北京: 中国铁道出版社, 2000: 368−424. WU Hongqing, REN Xia. The finite element analysis of structure[M]. Beijing: China Railway Press, 2000: 368−424.

[21] 王新敏.ANSYS工程结构数值分析[M]. 北京: 人民交通出版社, 2007: 30−100. WANG Xinmin. ANSYS numerical analysis of engineering structures[M]. Beijing: China Communications Press, 2007: 30−100.

Longitudinal displacement function and shear flow of thin-walled box girders in bending

LI Liyuan, ZHOU Maoding, ZHANG Yuanhai

(School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

On the basis of the bending theory of thin-walled box girders, and in combination with the hypothesis for solving plane stress problems in elasticity theory, bending longitudinal displacement function considering each plate in-plane shear effect of thin-walled box girders was derived. At the same time, the shear lag warping displacement function was derived theoretically. The displacement mode considering in-plane shear effect of all plates was simplified and solved by using the principle of energy variation and Timoshenko hypothesis of deep beam theory, and the numerical example was given. The results show that the calculated stresses at mid-span cross section of a simply supported box girder by using the displacement mode with shear effect are in a good agreement with the measured values and the finite element analysis results. There are large differences between the calculated shear stresses which considering all plates’ shear effect and the traditional calculation results. Compared with previous methods, the shear stress and deflection calculated in this research are more accurate; what’s more, the shear stress of webs and deflection of the box girder increases, the biggest growth reaches 21%.

thin-walled box girder; in-plane shear effect; energy variation method; deflection; shear flow

10.11817/j.issn.1672-7207.2015.10.049

U448.213

A

1672−7207(2015)10−3928−08

2015−02−11；

2015−04−25

国家自然科学基金资助项目(51268029，51068018，51468032)(Projects (51268029, 51068018, 51468032) supported by the National Natural Science Foundation of China)

张元海，博士，教授，博士生导师，从事薄壁箱梁与特殊桥梁设计理论研究；E-mail：zyh17012@163.com

(编辑 陈爱华)