梅涅劳斯（Menelaus）定理的十种证明

杨春波

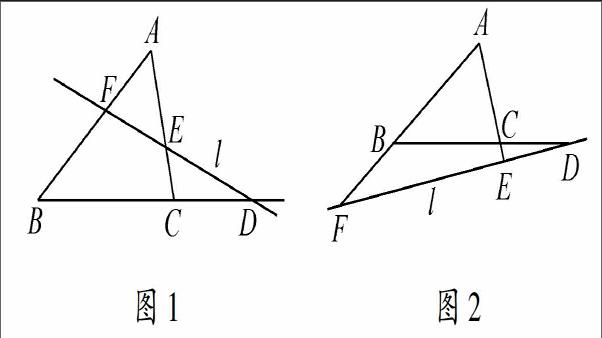
梅涅劳斯定理是平面几何学以及射影几何学中的一项基本定理，具有重要作用，其具体内容为：设直线l分别与△ABC的三边（或边的延长线）相交于点D、E、F，则有AFFB·BDDC·CEEA=1.

直线l与三角形的三边相交，有两种情形：（1）其中两个交点在边上，一个交点在边的延长线上，如图1；（2）三个交点均在边的延长线上，如图2.图1图2

梅涅劳斯定理在处理直线形中线段长度比例的计算时，尤为快捷.值得一提的是，其逆定理也成立，可作为三点共线、三线共点等问题的判定方法.下面给出梅涅劳斯定理的十种精彩证明，证明中仅以图1作为示例.

证法1平行线法

如图3，过点C作CG∥DF交AB于点G，则BDDC=BFFG，CEEA=GFFA，故

AFFB·BDDC·CEEA=AFFB·BFFG·GFFA=1.

图3图4

证法2共边定理法

如图4，由共边定理知AFFB·BDDC·CEEA=AEDBED·BEDCED·CEDAED=1.

证法3共角定理法

如图1，由共角定理知

△AEF△BFD=AF·EFFB·DF，BFDCDE=BD·DFDC·DE，CDEAEF=DE·CEEA·EF，

三式相乘得1=AF·EFFB·DF·BD·DFDC·DE·DE·CEEA·EF=AFFB·BDDC·CEEA，得证.

注共边定理和共角定理源自于张景中院士的面积法[1]，下面是定理的具体内容.

共边定理若直线AB和PQ相交于点M（如图5，有4种情形），则有PABQAB=PMQM.

图5图6

共角定理如图6，若∠ABC和∠XYZ相等或互补，则有ABCXYZ=AB·BCXY·YZ.

证法4辅助平面法

如图7，过截线l作平面α，设顶点A、B、C到该平面的距离分别为dA、dB、dC，则有

AFFB=dAdB，BDDC=dBdC，CEEA=dCdA，

三式相乘即得证.

图7图8

该证明曾在网上被大量转载，被称为令人感动的证明.文[2]中也收录了该证明，并称“上面这种方法恐怕是最帅的一种了.它解决了其他证明方法缺乏对称性的问题，完美展示了几何命题中的对称之美”.其实，何必要在空间中作一个辅助平面呢，且看单墫先生在文[3]中给出的精彩证明.

证法5垂线法

如图8，分别自A、B、C向l作垂线，设垂线段的长度分别为p、q、r，则

AFFB=pq，BDDC=qr，CEEA=rp，

三式相乘即得证.

证法6正弦定理法

在△AEF、△BDF、△CDE中，由正弦定理得

AFFB·BDDC·CEEA=AFEA·BDFB·CEDC=sin∠AEFsin∠AFE·sin∠BFDsin∠FDB·sin∠EDCsin∠CED，

因∠AEF=∠CED，∠BFD+∠AFE=180°，∠EDC=∠FDB，故上式右端乘积为1，得证.

证法7向量法

设AF=λFB，BD=μCD，CE=γEA，即证λμγ=1.

DE=DC+CE=1μ-1CB+γγ+1CA=1μ-1AB-（1μ-1+γγ+1）AC；

EF=AF-AE=λλ+1AB-1γ+1AC.

由D、E、F三点共线，知DE与EF共线，故1μ-1·1γ+1=λλ+1（1μ-1+γγ+1），整理即λμγ=1.

证法8坐标法

设A（x1，y1），B（x2，y2），C（x3，y3），且AF=λFB，BD=μDC，CE=γEA，则

F（x1+λx21+λ，y1+λy21+λ），D（x2+μx31+μ，y2+μy31+μ），E（x3+γx11+γ，y3+γy11+γ）.

设直线l的方程为ax+by+c=0，代入点F的坐标，即

ax1+λx21+λ+by1+λy21+λ+c=0，

解得λ=-ax1+by1+cax2+by2+c，同理有

μ=-ax2+by2+cax3+by3+c，γ=-ax3+by3+cax1+by1+c，于是λμγ=-1，即AFFB·BDDC·CEEA=1.

这样的坐标法并没有建立坐标系，而是直接设出点的坐标，运算过程对称、简洁！

证法9质点法[4]

设（1+r）F=A+rB，（1+s）E=A+sC，两式相减消去点A得

（1+r）F-（1+s）E=rB-sC，

此式表明FE与BC交于一点，即（r-s）D=rB-sC，于是AFFB·BDDC·CEEA=r·sr·1s=1.

质点法直接让几何学里最基本的元素——点参与运算，稍微修改就可得向量证法：在△ABC所在平面内任取一点O，设AF=rFB，AE=sEC，则有

（1+r）OF=OA+rOB，（1+s）OE=OA+sOC，

两式相减得（1+r）OF-（1+s）OE=rOB-sOC，又FE与BC交于点D，故有

rOB-sOC=（r-s）OD，

则BD=srCD，于是AFFB·BDDC·CEEA=r·sr·1s=1.

以上过程中点O是任意的，并不起实质性作用，完全可以省略不写，用一个字母表示向量，这就是质点几何了.质点法的最新研究成果是建立了能处理希尔伯特交点类命题的仿射几何机器证明算法MPM（Mass-Point-Method），并编写了Maple程序，验算了几百个非平凡命题，不仅效率高，程序自动生成的证明也有可读性，这一工作是广州大学邹宇博士在张景中院士的指导下完成的.最后给出梅涅劳斯定理的机器证明，算作第十种证法.

证法10机器证明Points（A，B，C）；Mratio（D，B，C，r1）；Mratio（E，C，A，r2）；Inter（F，D，E，A，B）；ratioproduct3（A，F，F，B，B，D，D，C，C，E，E，A）A，B，C（1+r1）D=B+r1 C（1+r2）E=C+r2 AF=（A B）∩（D E）D-r1（1+r2）E[]1+r1=-r1r2 A1+r1+B1+r1F=r1r2 A-1+r1 r2-B[]-1+r1 r2A-F=-F-B[]r1 r2B-D=r1（D-C）C-E=r2（E-A）[AF][BD][CE][][FB][DC][EA]=-1

参考文献

[1]彭翕成，张景中.仁者无敌面积法[M].上海：上海教育出版社，20116.

[2]顾森.思考的乐趣：Matrix67数学笔记[M].北京：人民邮电出版社，20127.

[3]单墫.平面几何中的小花[M].上海：华东师范大学出版社，20113.

[4]彭翕成.向量、复数与质点[M].合肥：中国科学技术大学出版社，20145.

[5]张景中，彭翕成.绕来绕去的向量法[M].北京：科学出版社，20109.