弹道导弹目标特性分析及雷达回波模拟*

孟路稳，周 沫，察 豪，温东阳，张润哲，朱倪瑶

(海军工程大学电子工程学院，武汉430033)

1 引言

弹道导弹具有射程远、突防性强、杀伤破坏威力大等特点，已成为现代防御系统的重大威胁。根据弹道导弹从发射点到目标落点过程中的受力情况，可将导弹的飞行过程分为助推段、自由段和再入段[1]。自由段是弹道导弹飞行时间最长的一段，约占导弹飞行时间的80% ～90%，故自由段被认为是弹道导弹防御的关键阶段[2]。地基雷达在弹道导弹防御系统中起着重要的支撑作用，能够探测弹头目标进而确定弹头的结构特征、运动特性等。导弹的雷达回波数据是研究弹道导弹探测和识别的基础，然而在外场实测回波数据具有代价高、干扰因素多等缺点，因此导弹的雷达回波模拟仿真是一种有效解决方案。

文献[3]从雷达散射截面和一维距离像两方面对建立的空间目标进动模型和宽带雷达回波信号模型进行了验证。文献[4]基于移动散射点模型得到了宽带雷达中段目标的回波模型。但由于弹头高速运动，对脉冲内的影响不能忽略，上述文献均未对此进行考虑，并且大多文献仿真的回波信号是针对弹头平动补偿后的进动情况，没有考虑平动的影响。

本文分别对弹头的运动特性、结构特性、电磁散射特性进行分析，建立自由段弹头的平动模型和微动模型;以此为基础，引入准静态的思想，考虑散射中心的散射强度和空间位置随姿态变化的特性，建立了弹头的宽带线性调频(Linear Frequency Modulation，LFM)雷达回波模型。仿真回波不仅蕴含弹头的运动特性以及目标散射特性随姿态、频率等的变化，同时也包含弹头的微动调制特性，对回波数据进行处理得到的弹头距离像验证了仿真的有效性。

2 自由段弹头的平动模型

在满足椭圆弹道基本假设[5]下，自由段导弹飞行在由速度矢量和地球引力矢量所决定的弹道平面内，如图1所示。其椭圆弹道方程为[6]

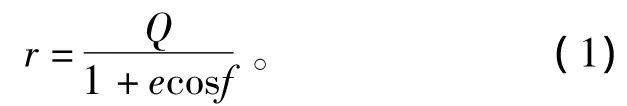
式中，r为地心矢径，e为偏心率，Q为半通径，f为极角。

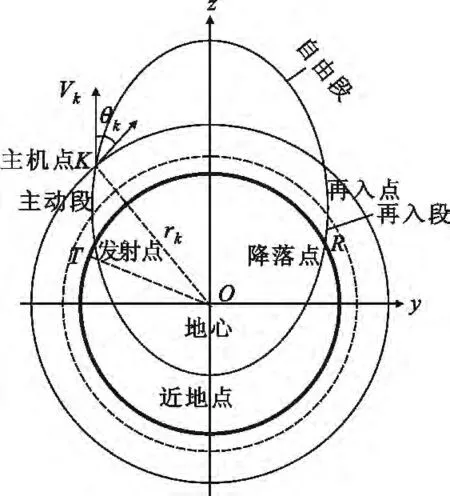
图1 弹道导弹的椭圆轨道示意图Fig.1 Sketch map of elliptical orbit of ballistic missile

自由段导弹的飞行轨迹与导弹关机点有关。设导弹关机点与地心的距离为rk，速度为Vk，弹道倾角为 θk，则由文献[7]可得

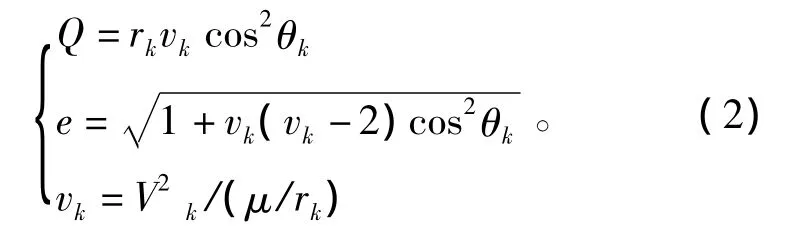
式中，vk为一中间变量;μ为地心引力常数，其值为μ =3.986 ×1014m3/s2。

若保证导弹飞行轨道为椭圆轨道，则偏心率需满足e＜1。此时椭圆轨道的长半轴a和短半轴b分别为

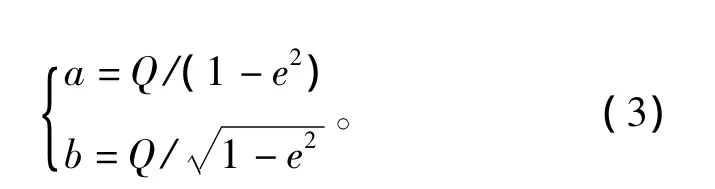
为得到弹道导弹在不同时刻的速度和位置信息，需借助开普勒方程进行求解。开普勒方程[6]为

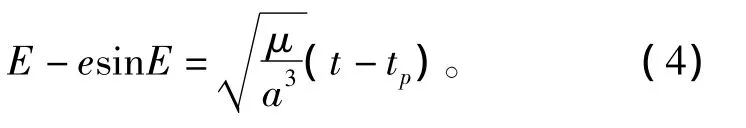
式中，E为偏近地角，具体定义见文献[5];tp为导弹飞过近地点的时间。

导弹的任一时刻的速度和速度倾角为

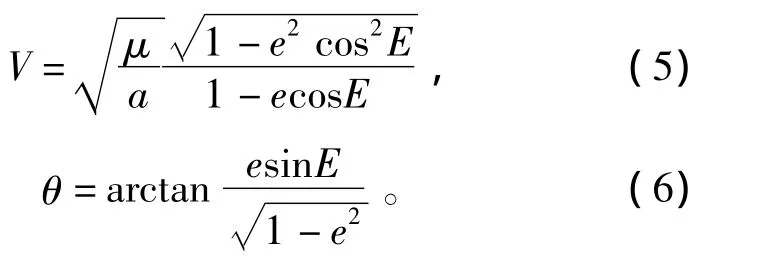
式中，地心矢径r与偏近地角E的关系为

实际情况下，由于弹道导弹攻击目标时导弹的发射点和落点位置是预先设定好的，所以本文事先设定导弹的发射点和落点的位置，然后求解出导弹关机点处的运动参数，进而求解出自由段导弹的运动参数。

设导弹发射点和落点位置的经纬度分别为(λT，φT)、(λR，φR)，则导弹发射点与落点之间的射程角βc可表示为

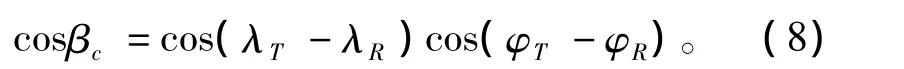
由文献[6]可知，射程角与弹道运动参数的关系表达式为

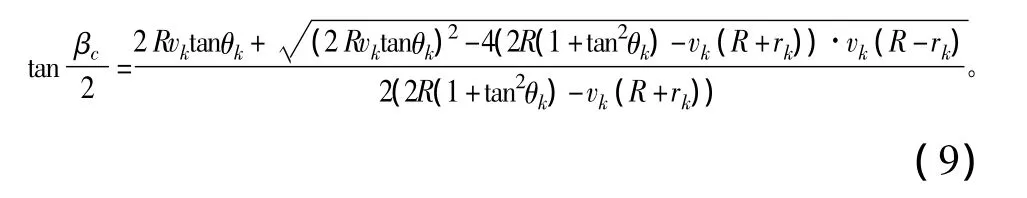
由式(8)、(9)可以看出，在发射点和落点预先设定的情况下，若已知导弹关机点至地心的距离rk，则导弹的关机点速度和其速度倾角的关系就是确定的。

设定弹道导弹的发射点位于东经45°、北纬0°，落点位于东经135°、北纬0°，导弹关机点距离地心的距离为rk=6.471×103km，则可得出关机点处的速度与速度倾角的关系曲线，如图2所示。

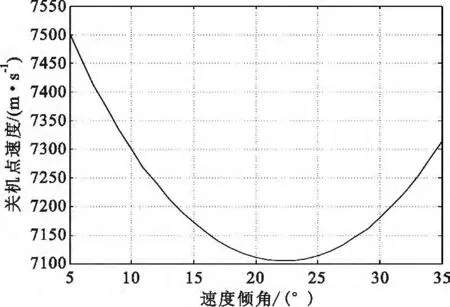
图2 关机点速度与速度倾角的关系曲线Fig.2 Curve of shutdown point speed and angle

从图2可以看出，对于预定的发射点和落点，若知道导弹关机点距地心的距离，则存在一个最佳关机点速度倾角θkopt，当导弹以此速度倾角进入自由段时，所需要的速度最小，导弹的能量得到了充分的利用，此时的弹道称为最小能量弹道[5]。因此在进行弹道设计时，应使θk最可能地控制在最佳速度倾角θkopt附近。鉴于此，本文仿真采用最小能量弹道，易得最佳速度倾角为22.23°。至此，若已知导弹的发射点和落点以及导弹关机点至地心的距离，应用以上各式可求解出任一时刻t导弹所具有的运动参数r(t)、V(t)、θ(t)。现将导弹运动参数解算的步骤归纳如下:

step 1:由弹道导弹的发射点和落点位置以及rk，根据式(5)、(6)、(8)、(9)求出最小能量弹道条件下导弹关机点处的运动参数Vk、θk;

step 2:根据式(2)、(3)求解椭圆弹道的几何参数 Q、e、a、b，并由式(7)求解偏近地角 Ek;

step 3:取导弹关机点时间tk=0，由式(4)求得导弹经过近地点的时间tp;

step 4:对于任意时刻 t，将求得的 e、a、tp代入式(4)，采用迭代法[10]反解开普勒方程，进而求出任一时刻t所对应的偏近地角E(t);

step 5:由式(1)、(5)、(7)求得任意时刻 t导弹的运动参数 r(t)、V(t)、θ(t)。

3 弹头微动模型

实际飞行的弹头除了作轨道运动外，还存在微动特性[8]，图3给出了弹头目标的微动模型。弹头在本体坐标系O－xyz中沿Oz放置，坐标原点为弹头质心。弹头的微动包括绕弹体对称轴Oz的自旋以及绕进动轴ON的进动，其中设自旋角速度矢量为wspin，大小为Ω;进动角速度矢量为 wconi，大小为wn。Q－ABC为雷达坐标系，雷达位于坐标原点Q;同时为便于处理，引入了参考坐标系O－XYZ，原点为O，其始终与雷达坐标系平行。

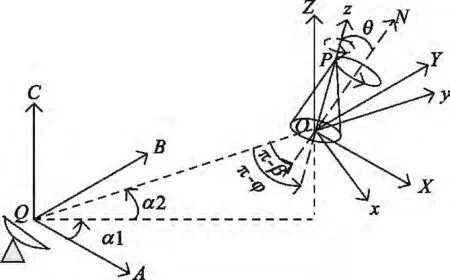
图3 弹头的微动模型Fig.3 Micro model of a warhead

设初始时刻点P在本体坐标系中的坐标为r0，则其在参考坐标系的坐标为

式中，Rotinit为目标坐标系与参考坐标系之间的旋转变换矩阵，其由初始时刻两者之间的欧拉角确定。并由Euler－Rodrigue旋转公式可得自旋转换矩阵

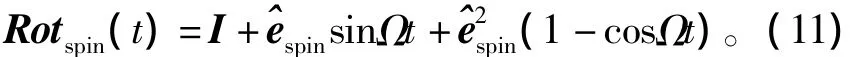
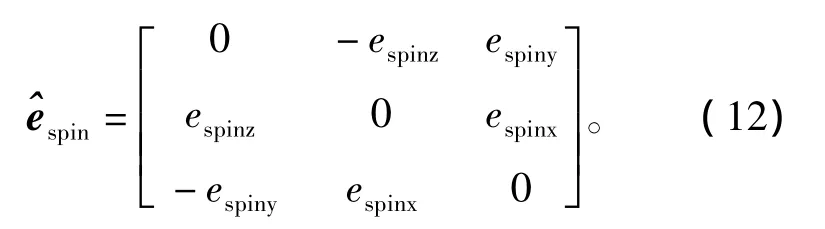
同理，可得t时刻的进动转换矩阵Rotconi(t)。故考虑弹头自旋和进动时，点P在参考坐标系中的坐标为

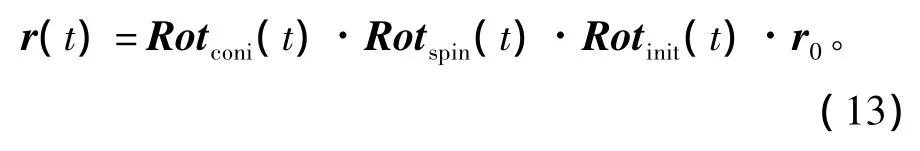
若初始时刻弹头在雷达坐标系中的方位角和俯仰角分别为α1、α2，雷达相对弹头的径向矢量为n=(cosα2cosα1，cosα2sinα1，sinα2)，则点 P 在径向上的投影为

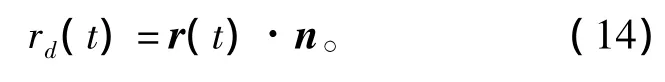
图3中夹角φ为弹头的视线角;θ角为弹头纵对称轴与进动轴之间的夹角，即进动角;雷达视线与弹头进动轴之间的夹角为β，若弹头不存在平动，则进动轴与雷达视线的夹角为一常数，此时β角称为平均视线角。而实际情况中，平均视线角是时刻变化的，需要根据坐标系的转换以及空间几何关系确定。则由图3中的空间几何关系可得弹头视线角的表达式为

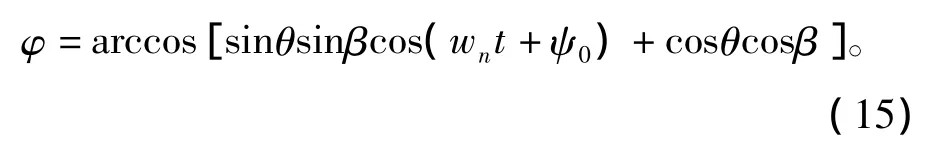
式中，wn为旋转角速度，ψ0为初始相位角。

4 弹头的宽带LFM雷达回波模型

归一化线性调频信号[9]可表示为

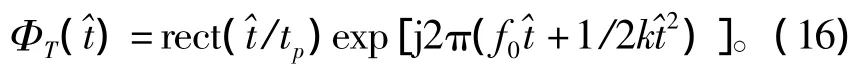
式中，tp为脉载频;rect(·)为矩;f0为载频;rect(·)为矩形包络;=t－nT，T为脉冲周期，n为脉冲周期数。若弹头相对于雷达波长处在光学区，此时弹头的尺寸远大于波长，弹头不能再被当作点目标进行处理，而是等效为多散射中心进行处理[10]。由于脉冲宽度多在微秒级，弹头的宏观运动速度相对光速是很小的，可认为弹头在脉冲宽度内作匀速直线运动，同时引入准静态技术的思想，即把每个脉冲看作是处于平衡状态，而整个脉冲串是由一系列接替的平衡状态组成，如图4所示。图中显示的是每一脉冲周期开始时刻参考中心对应的距离和多普勒频率。

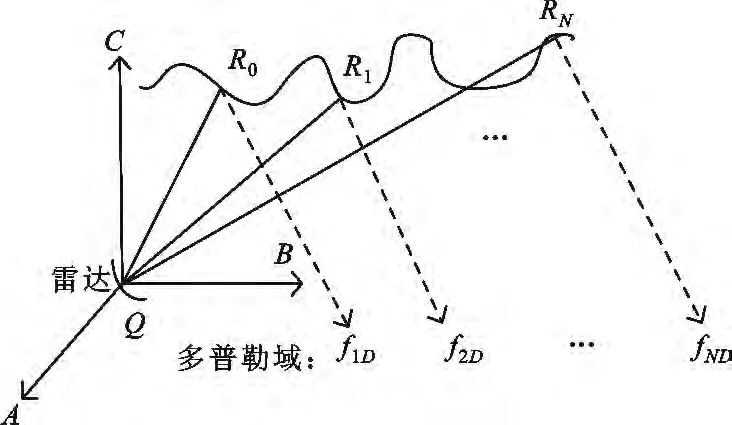
图4 准静态技术示意图Fig.4 Curve of quasi－ static

设弹头由M个散射中心组成，且在第一个脉冲开始时刻的径向速度为vr。考虑脉内运动对回波的影响，则可得第一个脉冲经弹头反射得到的回波信号为

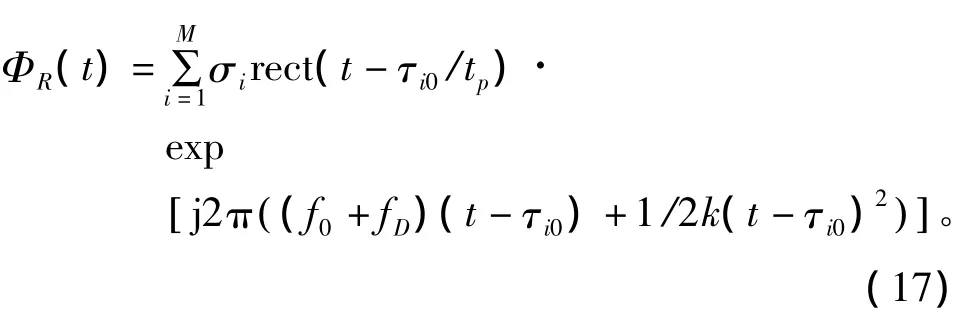
式中，τi0为第i个散射中心与雷达的距离引起的时延，其值为τi0=2Ri0/t;σi为散射强度;fD为由径向速度引起的多普勒频率，其值为fD=ftD+fmD，其中ftD=2vr/λ为平动引起的多普勒频率，λ为波长，fmD为进动引起的微多普勒频率，其值为

式(17)为第一个脉冲的反射回波，对于整个脉冲串，只需求出每个脉冲开始时刻对应的径向距离和多普勒频率，进而得到整个脉冲串的回波信号。

5 仿真结果与分析

设雷达的载频f0=10 GHz，脉冲宽度tp=1 μs，带宽Β=100 MΗz，脉冲重复周期Τ=1 ms。并设置雷达位于东经43°、北纬6°，导弹关机点距离地面100 km，导弹发射点位于东经45°、北纬0°，落点位于东经135°、北纬0°。仿真弹头采用文献[10]中的平底锥弹头，其结构如图5所示，其中设置参数a=1 m ，b=0.06 m ，γ=12°。平底锥弹头主要有3个散射中心，分别是球冠和底部边缘上的两点，各个散射中心的散射强度随姿态角的变化而变化，并且选取底部中心点为相位参考点。弹头的进动角为θ=10°，进动角速度为 wn=0.2π rad/s。

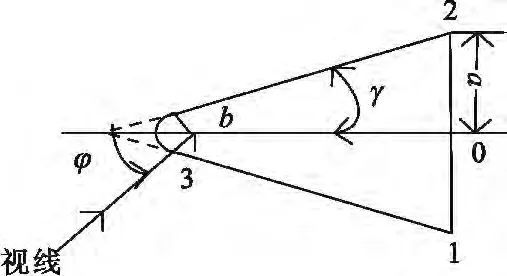
图5 弹头结构图Fig.5 Structure of a warhead

由上可得自由段弹头的最小能量弹道如图6所示。可以看出弹头的轨道呈椭圆形，关机点距离地面100 km，与理论分析一致。同时给出弹头视线角随观测时间的变化图，如图7所示。

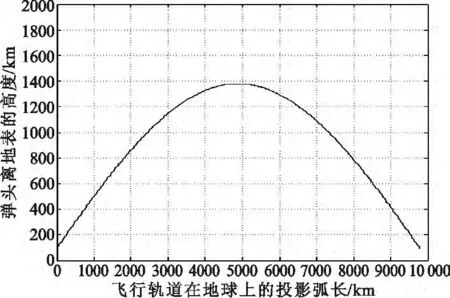
图6 弹头的最小能量弹道Fig.6 Minimum energy trajectory of a warhead

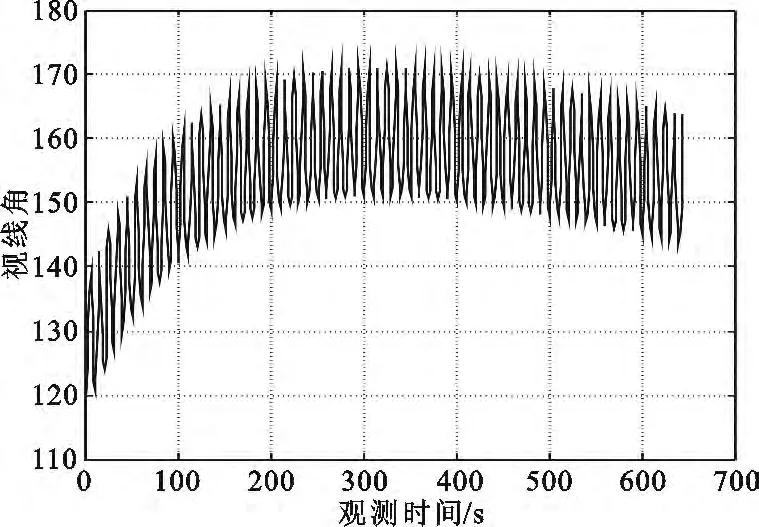
图7 弹头视线角Fig.7 Attitude angle of a warhead

从图7可以看出，弹头姿态角总体上先增大后减小，这是由弹头质心平动引起的，同时其上叠加有周期性振荡，这是由弹头进动引起的。

下面对未考虑微动和考虑微动两种情况下的弹头回波进行仿真，其波形分别如图8和图9所示。

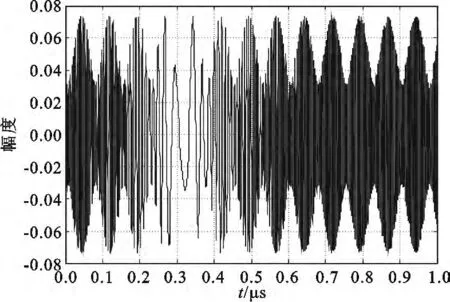
图8 未考虑微动时弹头的回波Fig.8 Warhead echo when micro is not considered

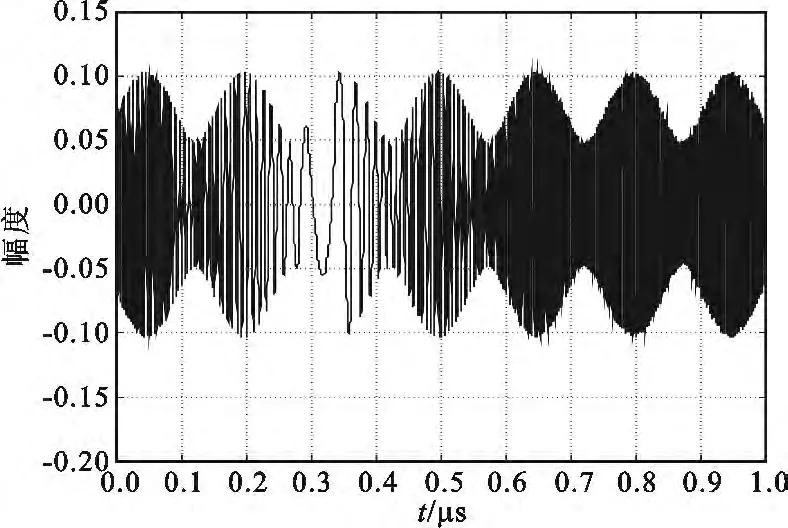
图9 考虑微动时弹头的回波Fig.9 Warhead echo when micro is considered

从图8和图9中弹头回波波形上均不能看出弹头的结构特征，但对比两种情况下的回波波形可以发现:与未加微动时相比，加微动后弹头回波波形的轮廓发生了变化，并且其幅度值相对于未加微动时增大了。这是由于未加微动和加微动两种情况下的弹头姿态角不一样，造成弹头散射中心的散射强度以及在雷达视线上的空间分布发生了变化，其反应在回波上就是两种情况下的回波强度和轮廓不一致。为进一步说明两种情况下弹头回波的区别，下面对得到的两种回波数据进行处理，得到未加微动时弹头的一维距离像(High Resolution Range Profile，HRRP)和加微动时弹头的一维距离像，其结果分别如图10和图11所示。

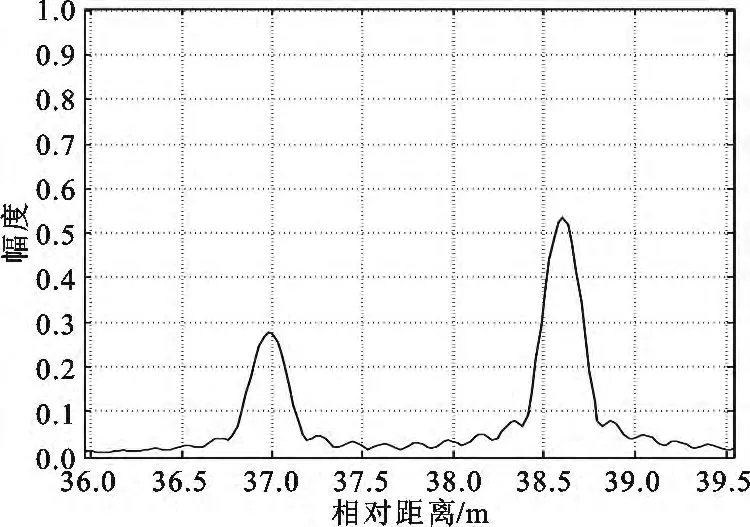
图10 未考虑微动时弹头的一维距离像Fig.10 Warhead HRRP when micro is not considered

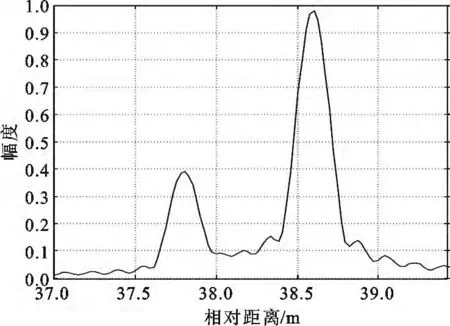
图11 考虑微动时弹头的一维距离像Fig.11 Warhead HRRP when micro is considered

对比图10和图11可知，两种情况下弹头的一维距离像中均出现两个峰值点，可以分析出此时对弹头散射特性起作用的有两个散射中心。由图7可知，在观测时间内，弹头的姿态角变化范围为[120.1°，170.9°]，理论计算可知此时只有散射中心1、2起作用，散射中心3的散射强度为0，仿真结果与理论计算结果一致，说明了仿真的正确性。同时也可以看出，两个距离像中峰值点的幅度以及峰值点之间的相对距离不一致，说明了两种情况下弹头相对于雷达视线的姿态角不同，与对弹头回波分析得出的结果一致，验证了所建模型的可行性。

6 结束语

本文建立了自由段弹头的最小能量弹道以及弹头的微动模型，并对弹头结构进行了分析，以此为基础给出了弹头的宽带LFM雷达回波信号模型。仿真结果表明:本文模型能够较好地复现自由段弹头的回波信号，反映出弹头的运动特性以及弹头散射特性随姿态角变化的特点，同时也能反映微动调制引起的弹头姿态角、距离像的变化，为后续自由段导弹目标的特征提取和目标识别奠定了基础。

[1]康猛，王春花，郝明，等.弹道目标进动周期特征提取研究[J].现代雷达，2010，32(11):29 －32.KANG Meng，WANG Chunhua，HAO Ming，et al.A Study on Precession－period Extraction Method of Ballistic Targets[J].Modern Radar，2010，32(11):29 －32.(in Chinese)

[2]刘维建，陈建文.弹道类目标进动周期特征提取方法研究[J].现代雷达，2009，31(7):62 －68.LIU Weijian，CHEN Jianwen.A Study on Precession Period Extraction Method of Ballistic Targets[J].Modern Radar，2009，31(7):62 －68.(in Chinese)

[3]马超，许小剑.空间进动目标的宽带雷达特征信号研究[J].电子学报，2011，39(3):637 －642.MA Chao，XU Xiaojian.Modeling of Wideband Radar Signature for Precession Space Objects[J].Acta Electronica Sinica，2011，39(3):637 －642.(in Chinese)

[4]薛爱军，王晓丹，宋亚飞，等.中段目标宽带雷达回波仿真及分析[J].计算机仿真，2013，30(8):23－26.XUE Aijun，WANG Xiaodan，SONG Yafei，et al.Simulation and Analysis of Radar Echo Based on Moving Scattering Center Model[J].Computer Simulation，2013，30(8):23 －26.(in Chinese)

[5]张毅，肖龙旭，王顺宏.弹道导弹弹道学[M].2版.长沙:国防科学技术大学出版社，2005.ZHANG Yi，XIAO Longxun，WANG Shunhong.Ballistic Missile Ballistics[M].2nd ed.Changsha:National University of Defense Technology Press，2005.(in Chinese)

[6]胡万秋.弹道中段目标进动特征提取方法研究[D].长沙:国防科学技术大学，2010.HU Wanqiu.Study on Precession Character Extraction in Ballistic Midcource[D].Changsha:National University of Defense Technology，2010.(in Chinese)

[7]呼玮，杨建军，龙光正，等.弹道导弹被动段动态RCS建模与仿真[J].电光与控制，2010，17(4):22 －25.HU Wei，YANG Jianjun，LONG Guangzheng，et al.Dynamic Modeling and Simulation of RCS for TBM’s Post－Boost Guidance Phase[J].Electronics Optics＆Control，2010，17(4):22 －25.(in Chinese)

[8]陈翱.基于RCS序列的弹道中段目标微动提取技术[J].现代雷达，2012，34(6):78 －81.CHEN Ao.A Micromotion Extraction Technique for Target in Intermediate Trajectory Based on RCS Sequence[J].Modern Radar，2012，34(6):78 －81.(in Chinese)

[9]孟路稳，周沫，曾浩，等.高分辨雷达目标回波信号模拟与分析[J].电讯技术，2014，54(10):1396 －1400.MENG Luwen，ZHOU Mo，ZENG Hao，et al.Simulation and analysis of target echo signal of high－resolution radar[J].Telecommunication Engineering，2014，54(10):1396 －1400.(in Chinese)

[10]黄培康，殷红成，许小剑.雷达目标特性[M].北京:电子工业出版社，2005.HUANG Peikang，YIN Hongcheng，XU Xiaojian.The Characteristics of Radar Target[M].Beijing:Publishing House of Electronics Industry，2005.(in Chinese)