一种关于牛奶的多阶段动态定价研究

沈超

（上海海事大学信息工程学院，上海　201306）

一种关于牛奶的多阶段动态定价研究

沈超

（上海海事大学信息工程学院，上海201306）

0　引言

牛奶在销售过程中，由于金黄色葡萄球菌的增多容易变质和腐败，而对牛奶在不同阶段的定价和调价是个不易掌握的问题。在超市里，一般袋装牛奶的保质期只有45天，盒装牛奶的保质期通常是3-6个月，在保质期内，商家要多次对牛奶进行调价以便更快地售完。因此，如何科学地降价、降多少价才是最合理的，既要对消费者的健康负责，又要确保商家的销售利益最大化。美国牛奶分级定价机制考虑的是地区、经济、法律法规等综合因素，而我们在定价时主要以食品安全和商家利益最大化为目标，来研究多阶段动态定价问题［1］。

我们已经研究出一种金黄色葡萄球菌生长模型，该模型具有很高的正确分类率，从中引出一个参数牛奶的质量指标。本文在建立多阶段定价模型时会引进这个质量指标参数，尝试用遗传算法求解，希望得到分阶段最优的价格决策。

遗传算法是以决策变量为运算对象的，通过生物上的染色体和基因等进行遗传操作，求解优化问题。遗传算法可以直接以目标函数为搜索信息，通过选择、交叉和变异等运算产生新一代群体，遗传算法易于找到收敛于问题的最佳解。遗传算法的应用研究比理论研究更为丰富，在众多科学和工程问题中都有广泛的应用前景。

1　基于金黄色葡萄球菌生长模型的多阶段动态定价研究

金黄色葡萄球菌生长模型是利用支持向量机和粒子群优化算法建模的，从模型中得到的状态值引入牛奶的质量指标参数，放在本文的定价模型中作为输入，质量指标参数能够准确地反映出牛奶新鲜和质量程度。

在支持向量机建模中，主要将金黄色葡萄球菌的生长状态分为不生长、生长和生长过渡三类，建立模型以预测分类。核函数是 RBF函数金黄色葡萄球菌的生长主要受温度、水活性、PH值的影响，温度、水活性、PH值作为输入，状态值作为输出。数据集分成训练集和测试集，建立训练集的模型并计算测试集的正确分类率，求出惩罚系数c和核宽度系数g，惩罚系数c是误差的惩罚度，核宽度系数g是支持向量间的相互影响程度。

在粒子群优化方法中，主要对支持向量机模型进行优化，就是求最优的c和g，粒子群算法在此就不作介绍。得到最佳的c为41.4394，g为6.9125，精度为92.57%。

本文引入的质量指标通过金黄色葡萄球菌生长模型预测的状态值求出，反映了牛奶中金黄色葡萄球菌的生长状态，其值在［0，1］之间。假设牛奶中共有100个金黄色葡萄球菌，有20个菌处于生长状态，另外80个处于不生长或生长过渡状态，则质量指标的值=（1-20）/100=0.8。

（1）质量指标

牛奶在销售过程中，随着金黄色葡萄球菌状态值的改变而慢慢变得不新鲜，消费者也越来越不愿意购买牛奶了。我们假设质量指标与销售数量是成正比的关系，随着质量指标的降低，销售数量也降低，为此商家也要降低各阶段的定价。当质量指标低于一定值时，说明牛奶必须下架了。

质量指标是由金黄色葡萄球菌生长模型得出的，金黄色葡萄球菌的状态值有生长、不生长和生长过渡三种状态，牛奶的质量指标与金黄色葡萄球菌的状态值有关，我们可以根据金黄色葡萄球菌生长模型预测得到状态值，计算出质量指标。质量指标越低，说明牛奶中金黄色葡萄球菌状态值为生长状态，则牛奶就有腐败变质的风险，这时商家就应该对牛奶进行降价销售。

随着时间的推移，新鲜牛奶必然要变得不新鲜的。真实的销售情况是，其质量指标是不断降低的，销售量也会降低。在这里，我们不详细考虑消费者的需求量，例如不同季节牛奶的需求量是不一样的。

（2）变量定义及假设

设牛奶的单位进货成本为c，牛奶的总进货量为T，第λ阶段卖出牛奶的数量为nλ，第λ阶段时牛奶的定价（销售价格）为pλ，各阶段的价格向量P=（p1，…，pN）。Fλ是牛奶的质量指标，反映了牛奶中金黄色葡萄球菌的状态，其值由金黄色葡萄球菌生长模型得到，Fλ在［0，1］区间，且设所有阶段的总收益为Y（P），另外假设质量指标与销售量是成正比且有线性关系的。

（3）零售商收益最大化模型

约束条件：0＜FN＜Fλ＜F1（F1=1，低于FN时牛奶变质），

则收益最大化的模型如下：maxP（Y（P）），T和P= （p1，…，pN）是决策变量。

之前有国内学者利用迭代法和LINGO软件求解优化问题，最后求出收入的最大值［2］。由于求解方法的局限性，对于优化问题我们考虑用遗传算法求解。

该模型实际上是求单目标多因素的最大值，所以我们拟用遗传算法求解。遗传算法使用目标函数作为适应度函数就可以确定进一步搜索的方向和范围，并且遗传算法可以求得收敛于问题的最佳解。

2　遗传算法

遗传算法（Genetic Algorithm，GA）的操作对象是染色体、个体等种群，每一个染色体都对应问题的一个解。从初始种群出发，利用适应度函数在种群中选择个体，使用交叉和变异来产生下一代种群，模仿生命的进化进行不断演化，直到满足期望的终止条件。遗传算法引入了以下概念：

（1）个体：染色体带有特征的实体，遗传算法的基本单位；

（2）种群：每代所产生的染色体总数称为种群，一个种群包含了该问题的一些解的集合；

（3）种群大小：在种群中个体的数量；

（4）适应度：表示某一个体对于环境的适应程度。

开始时，我们根据目标函数产生初始种群的大小。接着，计算种群中个体的适应环境的能力，即适应度值，给予种群一定的选择概率、交叉概率和变异概率，继续繁殖，再计算适应度值。直到得到的适应度值满足条件或达到迭代次数时终止，否则继续更新适应度值。最后输出收敛于问题的最佳解。

遗传算法流程图如下：

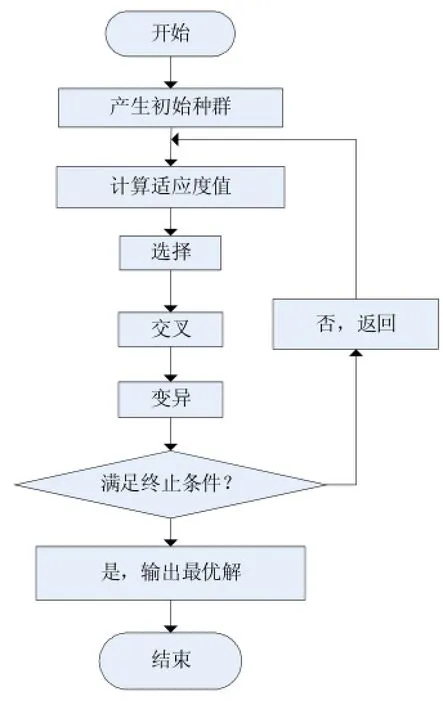
图1　遗传算法流程图

3　MATLAB仿真

在MATLAB r2013a环境安装遗传算法工具箱GAOT，编写目标函数放在工作目录下。再使用两个核心函数，初始种群的生成函数和遗传算法调用函数，得到最优解［3］。

国内学者在研究不等周期下批发量和多阶段定价时，通常建立二阶段、三阶段等不同的利润模型，求出最优批发量、每阶段的最优价格决策和最大利润［4］。而我们的研究中，牛奶的定价和调价是不定的，可能会在不等周期下进行调价。下面讨论二阶段下的情况：

二阶段下，牛奶在销售过程进行一次定价p1和一次调价p2，则收益函数为则Y（P）是关于p1、p2和T的线性关系方程。我们引入真实的销售情况，光明牛奶的莫斯利安一箱是200克×12盒，保质期是150天。

假设由金黄色葡萄球菌生长模型得到的F1=1和F2=0.8，另K=500，n1=500，n2=400，第一次定价p1=54（参考超市零售价格），成本c=30，则30·T，30≤p2＜p1＜54，T≥900，作为目标函数和约束条件。

实验里，我们设定初始种群的大小为10，迭代次数为25，设定符合市场行情的p1、p2和T的区间，认为p1在［30 54］，p2在 ［30 54］，T在［900 1200］，设选择概率是0.8，交叉概率是0.8，变异概率是0.08。在迭代到第7次时收敛并得到近似最优解，迭代次数与适应度值如图2所示：

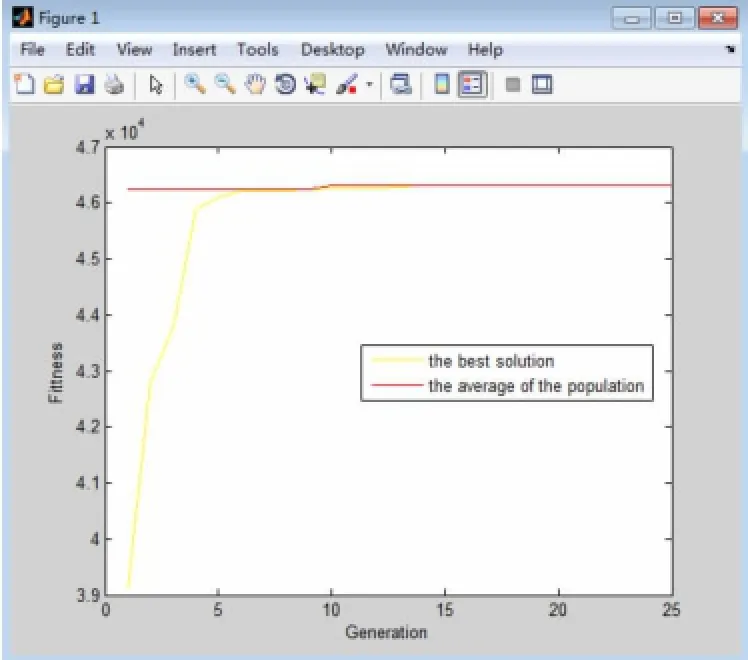
图2　迭代次数与适应度曲线（二阶段）

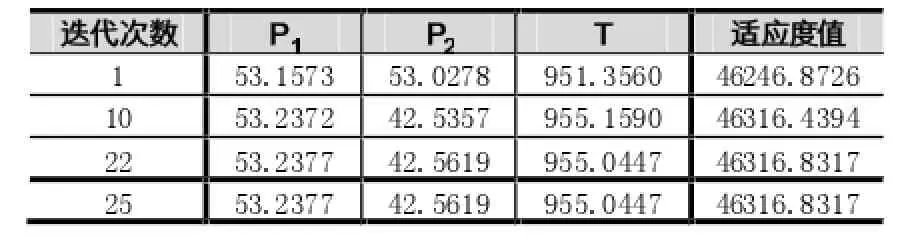
表1　二阶段价格决策

实验结果如表1所示，在第25次时，得到几乎不变的适应度值46316.8317。适应度函数值越大，则目标函数的目标值越大，此时为收敛于最佳解，得到了最大收益，得到近似最优解p1=53.2377，p2=42.5619，进货量T=955，收益Y（P）=14994。

三阶段下，牛奶在销售过程进行一次定价p1和两次调价p2、p3，则收益函数为

假设由金黄色葡萄球菌生长模型得到的F1=1和F2=0.8，另外K=500，n1=500，n2=400，n3=300，c=30，则Y作为目标函数和约束条件求解。

实验中，设定初始种群的大小为10，迭代次数为25，设选择概率是0.8，交叉概率是0.8，变异概率是0.08。设定符合市场行情的p1、p2、p3和T的区间，认为p1在［30 54］，p2在［30 44］，p3在［30 40］，T在［1200 1500］。在迭代到第8次时收敛并得到近似最优解，迭代次数与适应度值如图3所示：

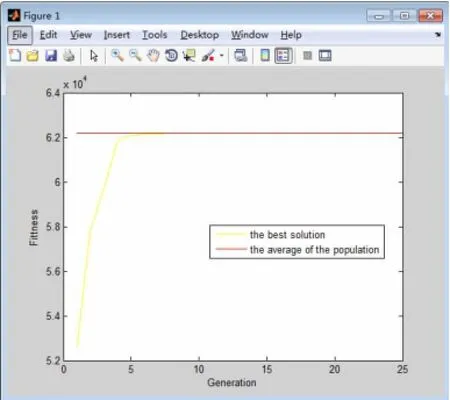
图3　迭代次数与适应度曲线（三阶段）

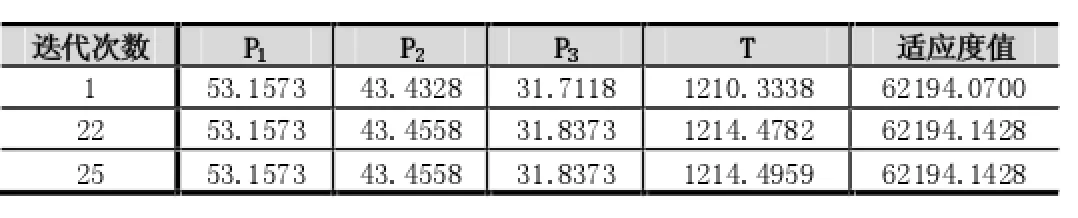
表2　三阶段价格决策

实验结果如表2所示，在第25次时，得到了最大的适应度值62194.1428，则目标函数的目标值最大，此时收敛于最佳解，求得近似最优解 p1=53.1573，p2= 43.4558，p3=31.8373，进货量T=1214.4959，收益Y（P）= 17077。

若牛奶在销售的过程中分为N阶段，需要作1次定价和N-1次调价。利用遗传算法工具箱求得的最优解可作为牛奶商家定、调价的有力依据。商家在得到收益最大化时，尽量让定价和调价变得合理，最优的价格决策在近似最优解周围附近浮动。

4　结语

本文中，我们引入牛奶的质量指标参数，建立了牛奶的多阶段定价模型，并用遗传算法求解。实验中，二阶段和三阶段的数值算例表明，遗传算法能够求得各阶段最优的价格决策和批发量，且使利益最大化，该多阶段动态定价模型能够科学地指导商家对牛奶进行定价和调价。

［1］Janet a Nuzum，Robert Yonkers.美国牛奶分级定价系统（J）.王责芳译.哈尔滨：中国乳品工业，2000

［2］潘驰宇.奶制品生产与定价（J）.北京：中国科技博览，2012

［3］雷英杰.MATLAB遗传算法工具箱及应用（M）.西安：西安电子科技大学出版社，2014

［4］胡觉亮.时变需求下非等周期多阶段定价与订货量的问题（J）.北京：纺织学报，2012

［5］刘晓峰.易逝品的动态定价机制与消费者策略行为研究［D］.上海：上海交通大学，2007

［6］唐磊.基于微生物预测的易腐食品定价研究［D］.南京：东南大学，2010

Revenue Maximization；Quality Index；Multi-Stage Dynamic Pricing Model；Genetic Algorithm；Price Decision

Research on Multi-Stage Dynamic Pricing about Milk

SHEN Chao
（College of Information Engineering，Shanghai Maritime University，Shanghai 201306）

1007-1423（2015）17-0018-05

10.3969/j.issn.1007-1423.2015.17.004

沈超（1988-），男，安徽芜湖人，硕士研究生，研究方向为微生物的数据挖掘

2015-04-09

2015-05-21

结合金黄色葡萄球菌生长模型的质量指标，提出一种牛奶的多阶段定价模型。模型以牛奶零售商的收益最大化为目标，以获得各个阶段最优的价格决策。利用遗传算法求解该模型，能够得到最优解，即各阶段最优的价格决策。

收益最大化；质量指标；多阶段动态定价模型；遗传算法；价格决策

Combined with Staphylococcus aureus growth model's quality index，carries out a multi-stage pricing model of milk.The model gets optimal price decision in each stage with the goal of revenue maximization for milk retailers.Uses genetic algorithm to sovel the model，it can get optimum results and optimal price decision in each stage.