一种变比例尺地图的导航算法

刘琰翔，陈子恬，陈俊熙

（华南师范大学计算机学院，广州　510631）

一种变比例尺地图的导航算法

刘琰翔，陈子恬，陈俊熙

（华南师范大学计算机学院，广州510631）

0　引言

变比例尺地图在日常生活十分常见，包括旅游地图、宣传材料和手绘地图等。这种地图不讲求准确性，通常强调重要建筑物和区域而省略其他的东西，并且在同一张地图中，所强调区域的比例尺可能会比其他区域大，以至整个图面的不同部分具有不同的比例尺。所以，地图往往是失真的，不能精确地反映各点的实际位置以及各条路径的实际方位和长度。这类地图是适合人们使用的，但它们并不适合用于导航，因为失真和无法估量的不准确性使地理编码和定位变得十分困难，无法作为基础地图简单地应用于传统的电子导航系统中。但是这种绘制灵活的变比例尺地图又比现今电子导航系统使用的等比例尺地图更明了生动，同时符合使用和审美的需求。

为了使这种灵活生动的变比例尺地图也能用于智能移动终端的电子导航系统中，本文提供了一种变比例尺地图导航算法来实现在这种变比例地图上定位。这种算法是使失真的变比例尺地图与智能手机上的定位功能相结合的关键技术。

1　相关工作

国内对于变比例尺地图的投影及可视化研究深入［1～3］，但在变比例尺地图导航这个领域很少有人研究。国际上，日本对此研究很多［4～6］，其中东京大学的几位学者提出了一种变比例尺导航的思想［4］。本文在此基础上，对算法进行改进并实现。

2　导航算法

本算法流程见图1，共有两个阶段：坐标转换和误差减免。

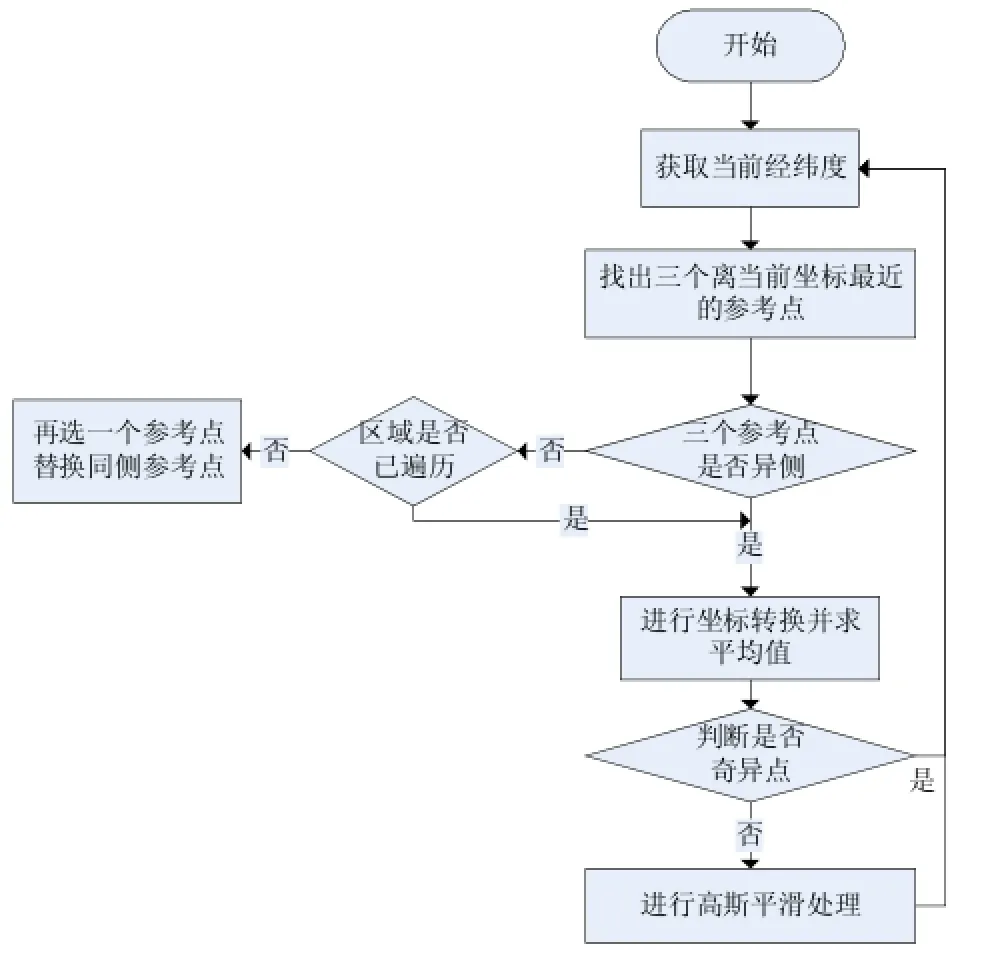
图1　导航算法流程图

首先，定义导航地图上的任意一点为p。

这里的c=（x，y）是地图上的像素坐标；l=（longitude，latitude）是地理坐标；因此，一张地图可以表示成如下形式：

通过手机或平板的GPS功能得到当前位置的l= （longitude，latitude），而需要得到的是该点在地图上的坐标c=（x，y）。首先必须存在足够多的参考点，而这些参考点的地理坐标和地图坐标都已经得知。然后，假设需要得知一点pm的地图坐标，首先就需要根据pm的地理坐标找到参考点中离它最近的两个坐标pm1和pm2。很明显，△cmcm1cm2和△lmlm1lm2是相似的（由于地球是个球体，所以△lmlm1lm2实际上是曲面三角形，但是因为各点之间的距离十分近，所以可以认为是一个平面三角形）。满足以下式子：

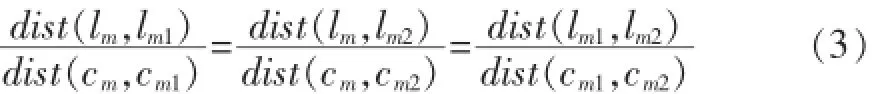
所以根据相似变换可以得到dist（lm，lm1），到dist（lm，lm2）和到dist（lm1，lm2）的距离，而lm1，lm2的坐标已经知晓。所以，问题就转变为两圆相交求相交点坐标了，如图2。由△cmkcm1和cmkcm2可以得到：

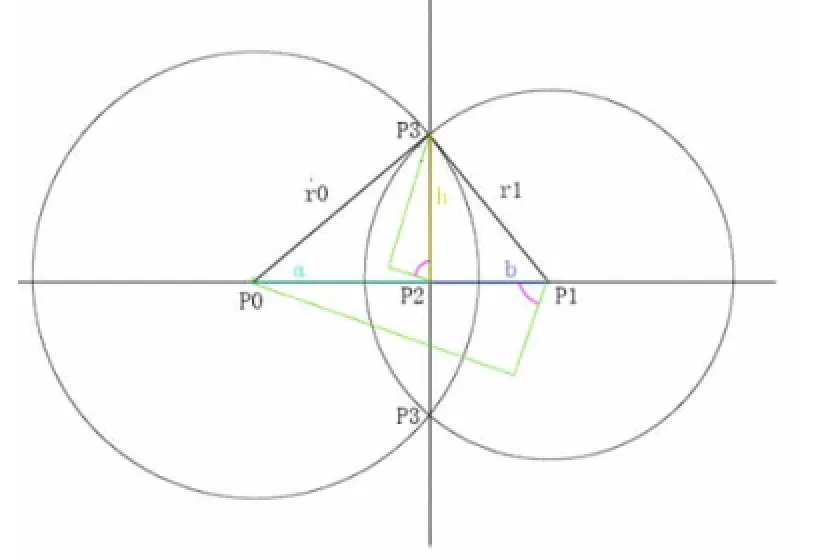
图2　两圆相交图

由d=a+b可以得到：

而cm1kcm2在同一直线上，所以有：

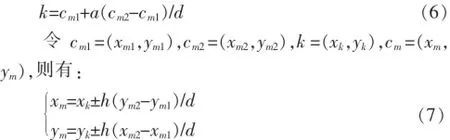
由此，便可以确定 cm=（xm，ym），该点就可以在等比例尺的地图上无偏差地转换坐标系。

自然，以上算法只能用于等比例尺地图的转换，简单方便且不需要太多参考点，但用在变比例尺地图上会出现如下误差：

（1）单方面伸缩误差

如图3所示，图3（A）是正常比例的图，而图3（B）拉伸了40%，图3（C）缩小了40%，根据该地图，点P在伸展后的地图对应的点应该是Pa，但是根据上面的算法得到的结果却会落在Pb。对于这种误差，实验发现如果游客和路线是在同一路径上的话，这种误差是可以接受的。所以在选取参考点的时候也需要尽量选取同一直线的参考点。

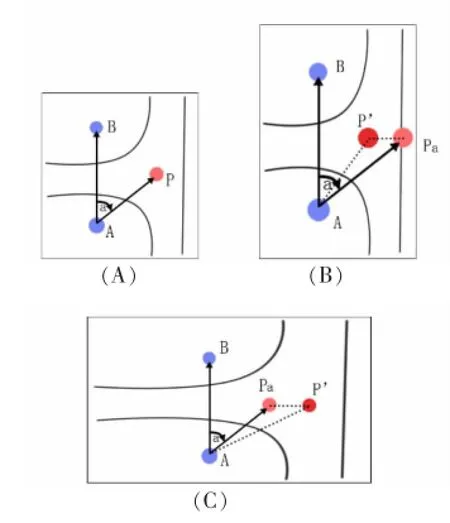
图3　单方面伸缩误差

（2）比例尺不同误差

如图4所示，图4（A）是正常尺度，而图4（B）为非常规尺度，图（B）放大了A点，缩小了B点，使得A点和B点的地图坐标发生改变，从而影响到了点P的定位。根据地图，正确的点P在变比例地图下应该落在Pa，而实际算法所得却得到Pb。

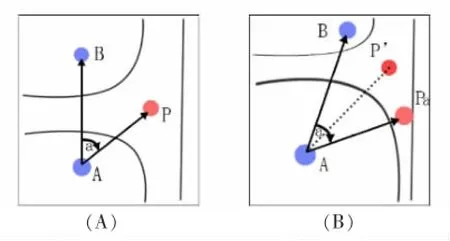
图4　比例尺不同引起的误差

（3）误差减免

对于不规则的地图，由于无法估量不同地图的失真，至今还没有一个统一的算法可以完全消除误差。然而，误差虽然无法完全免除，但本文提出一些方法可以进行减免。

主要改进如下：

①在选取参考点时，选取同一区域内的以待测点P为原点的不同象限内的三个坐标，并两两分别拿来确定P点坐标，然后将三次得到的坐标的平均值作为P点的地图坐标。

②去除奇异点。在每次坐标换算时，得到地图一点的坐标时，若与上一点坐标距离相差太大，则抛弃该点。

③在合理的地方设置更多的参考点。首先，景点坐标的设置应该设在各个景点的门口而非中间。另外，在导航过程中，用户基本上会沿着路径走，所以应该在主干路上设置更多的参考点，并且在道路的交叉路口和拐角处设置参考点。这些点多设置在景点密度不够大的区域。

④将地图分区域，加快查询参考点的效率。每次选参考点时都先将当前坐标与当前区域的中心点坐标进行比较，确定当前点落在当前区域的第几象限，然后将区域中心点换成该象限的中心点，一直进行此操作，直至区域足够小。

3　测试数据

以华师校园为例，在同一区域内测试参考点对坐标转换偏差距离的影响。

在同一区域内，在距离和位置合理的情况下，测试在同一点采取三个不同位置的参考点方案下与实际距离的偏差程度，然后再在不同地点测试，求平均值。

测试结果如表1所示。

表1　参考点对导航的影响

在同一区域内，在位置和数量合理的情况下，测试在同一点采取三个不同参考点距离的方案下与实际距离的偏差程度，然后再在不同地点测试，求平均值。测试结果如图5。

经测试发现，当合理参考点距离当前位置30米内时，导航误差是可以接受的。

在同一区域内，在距离和位置合理的情况下，测试在同一点采取三个不同参考点数量的方案下与实际距离的偏差程度，然后再在不同地点测试，求平均值。测试结果如图6。

测试发现，在半径50米的区域内当合理的参考点数量达到5个时，偏差程度便可以接受。

4　结语

为了解决传统导航在变比例尺地图上的无能为力，以及更好适应大众对于地图的需求，本文提出了一种能在变比例尺地图上导航的算法，并且从参考点位置、参考点距离和参考点数量三个方面对该算法进行测试。实验表明，在半径50米的区域内存在5个以上的参考点时，导航误差可以接受。另外，若存在3个相对于当前位置不同侧的参考点，导航效果更佳。

［1］闫超德，郭王，白建军，赵姗，武舫，贺添.变比例尺地图制图方法评述［J］.测绘科学，2014（3）：34～36

［2］李连营，司若辰，许小兰，李敏.基于地图投影思想的地图变比例尺可视化［J］.地理空间信息，2012（5）：161～163

［3］高平，冯严.导航点滴地图的多比例尺可视化的实现［J］.江西测绘，2010（4）：35～37

［4］Min Lu，Masatoshi Arikawa，Location-Based Illustration Mapping Applications and Editing Tools［J］.Cartographica.2013（48）：100-112

［5］Hideki Kaji，Masatoshi Arikawa.Personal Location Based Services on Place-enhanced Blog［J］.ACM Multimedia.2008（10）：917-920

［6］Min Lu，Masatoshi Arikawa.Map-Based Storytelling Tool for Real-World Walking Tour［J］.Progress in Location-Based Services.2013 （1）：435-451

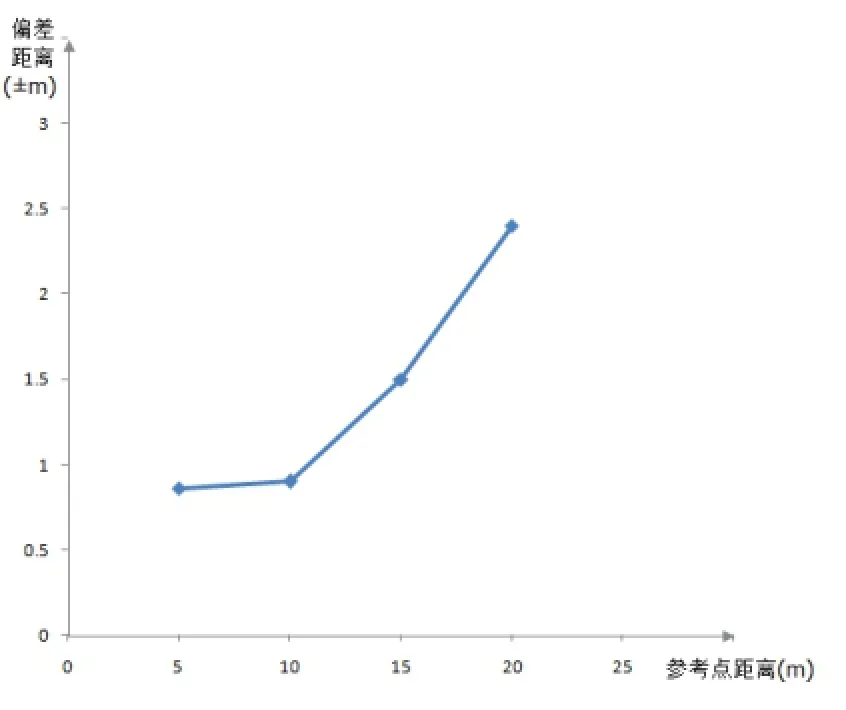
图5　参考点距离对导航的影响

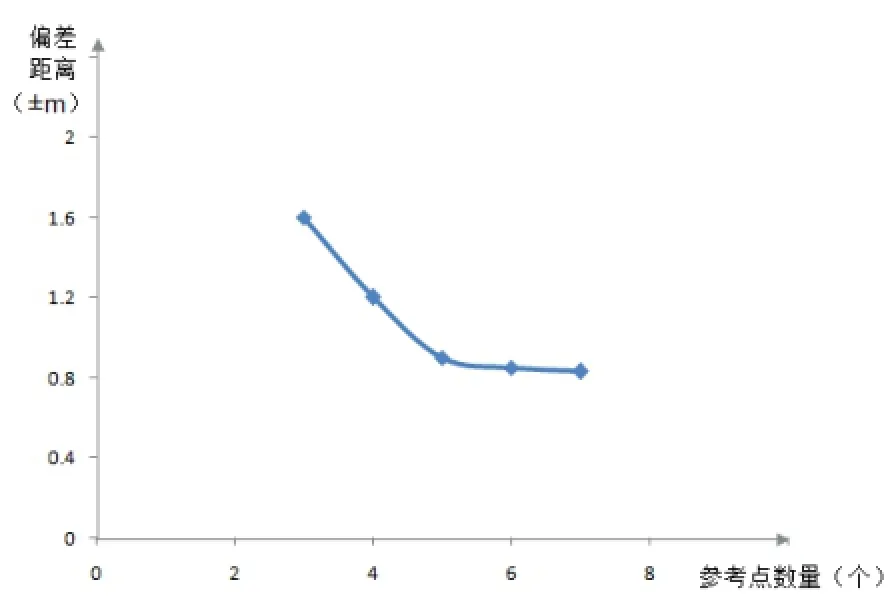
图6　参考点数量对导航的影响

Variable Scale Map；Coordinate Transformation；Deviation Reduction

Variable Scale Map Navigation Algorithm

LIU Yan-xiang，CHEN Zi-tian，CHEN Jun-xi
（College of Computer Science，South China Normal University，Guangzhou 510631）

1007-1423（2015）17-0014-04

10.3969/j.issn.1007-1423.2015.17.003

刘琰翔（1993-），男，广东揭阳人，本科，研究方向为算法设计与分析

陈子恬（1993-），女，广东汕头人，本科，研究方向为算法设计与分析

陈俊熙（1993-），男，广东云浮人，本科，研究方向为算法设计与分析

2015-04-03

2015-05-13

导航是目前基于位置的服务中尤为常见的一种服务。传统的导航服务应用于车辆驾驶和人们出行，而旅游业的发展对地图提出新的要求，也使得传统的导航服务不再适用。针对这种情况，提出一种可以应用于变比例尺地图上的导航算法。该算法的主要思想是坐标转换和误差减免。实验表明，该算法在变比例尺地图上误差小，能有效导航。

变比例尺地图；坐标转换；误差减免

Navigation is particularly common in location based service.The traditional navigation is used to driving and travel.The development of the tourism industry puts forward new requirements on the map，which makes the traditional navigation service is no longer applicable. Proposes a kind of navigation algorithm which can be used on the variable scale map.The main idea of the algorithm is the coordinate conversion and deviation reduction.The results show that the algorithm has little deviation on the variable scale map，and it can effectively navigate.