反复荷载作用下箱形压弯钢柱受力性能

李海锋，罗永峰，李德章，丁大益



反复荷载作用下箱形压弯钢柱受力性能

李海锋1, 2，罗永峰3，李德章4，丁大益5

(1. 华侨大学 土木工程学院，福建 厦门，361021；2. 福建省结构工程与防灾重点实验室，福建 厦门，361021；3. 同济大学 建筑工程系，上海，200092；4. 合肥市重点工程建设管理局，安徽 合肥，230001；5. 中国五洲工程设计集团有限公司，北京，100053)

分析16根箱形钢柱及85个数值计算构件的刚度退化特征、强度退化特征、荷载−位移变化曲线、破坏形态、应力分布规律，进而研究反复荷载作用下箱形压弯钢柱局部屈曲和整体失稳的相关作用机理。对试验数据及有限元计算结果进行统计分析，回归出反复荷载作用下箱形压弯钢柱稳定承载力的拟合公式。研究结果表明：当轴压比小于0.1或绕截面弱轴长细比小于40时，壁板局部屈曲对构件的受力性能起控制作用，腹板宽厚比对构件的延性、承载力退化、刚度退化均起主要作用；当轴压比大于0.2且绕截面弱轴长细比大于80时，构件整体失稳对其受力性能起控制作用，轴压比和长细比对构件受力性能的影响均非常显著。

箱形钢柱；拟静力试验；有限元模拟；相关屈曲；稳定承载力

箱形截面构件在2个主轴方向均有较好的抗弯性能，并且不易发生整体侧向扭转屈曲，比H形截面更适用于双向受弯构件。虽然箱形截面钢构件制作难度较大，但随着钢结构制作加工技术的进步，箱形截面钢构件的制作工艺技术日趋成熟。箱形钢构件已广泛应用于现代大型复杂钢结构之中，尤其在高层钢结构建筑和现代大跨度空间钢结构建筑中的应用越来越普遍。目前，关于反复荷载作用下箱形压弯钢柱受力性能方面的研究主要以多高层钢框架结构为研究背景，假定框架柱中间高度位置为构件的反弯点，取反弯点以下的框架柱作为研究对象，其研究成果主要集中在箱形短柱强度和局部屈曲方面。刘涛等[1]以多层钢框架结构中的箱形钢柱为研究对象，对常轴力、循环弯矩作用下箱形钢柱的滞回性能进行研究，揭示了箱形钢柱发生壁板局部屈曲后的受力性能。Su等[2−3]应用自编程序，对常轴力、循环弯矩作用下箱形截面短柱的滞回性能进行数值分析，并对数值分析结果进行了相应的试验验证。Wang等[4−7]等对高强钢焊接箱形柱的极限承载能力和滞回性能进行了试验研究与数值分析。Ge等[8−10]对反复荷载作用下钢桥墩的滞回性能进行了大量的试验研究与数值模拟工作，但其研究成果主要集中在圆柱形、箱形短柱承载力和局部屈曲方面。随着大尺寸焊接箱形钢构件在现代大跨度空间钢结构中的广泛应用，需针对大跨度空间结构中箱形钢柱的受力特点，进一步研究反复荷载作用下箱形钢柱的受力性能。实际上，大跨度钢结构的柱子要承受一定的轴力，同时还要承受很大的弯矩，致使此类钢柱的反弯点一般位于构件之外。对此类箱形钢柱的抗震性能进行研究时，需取整根箱形长柱为研究对象，研究其在柱顶轴力、弯矩、剪力作用下的受力性能，此方面的研究主要涉及反复荷载作用下箱形钢柱局部屈曲与整体失稳的相关作用[11]，国内外对此方面的研究较少。为进一步深入、全面地了解反复荷载作用下箱形钢柱的受力性能，本文作者根据大跨度空间结构中钢柱的受力特点，选取压弯柱为研究对象，对偏心常轴力、反复水平荷载作用下箱形钢柱的受力性能进行研究。通过分析16根箱形钢柱及85个数值计算构件的刚度退化特征、强度退化特征、荷载−位移变化曲线、破坏形态、应力分布规律等，进而研究箱形压弯钢柱的局部屈曲和整体失稳的相关作用机理，从而获得反复荷载作用下箱形压弯钢柱的主要受力特征，并提出箱形压弯钢柱的稳定承载力计算公式。

1 试验研究

为揭示反复荷载作用下箱形钢柱局部屈曲和整体失稳的相关作用机理，进行了16根箱形钢柱的低周反复加载试验。试验共设计了2类试件：第I类试件为箱形长柱，第II类试件为箱形短柱。为真实反映大跨度空间结构中箱形钢柱的受力特点，试验加载时考虑柱顶轴力、弯矩、剪力的共同作用。具体试验加载方法为在柱顶施加偏心竖向压力以等效柱顶轴力和弯矩的作用，同时在柱顶施加反复水平荷载以模拟地震和风荷载作用下柱顶的反复剪力作用。大跨度空间结构中箱形钢柱的研究方法如图1所示。试验加载示意图如图1(b)所示，试验过程及试验现象参见文献[12]。

(a) 大跨度空间结构的受力情况；(b) 箱形钢柱加载；(c) 横截面

1.1 刚度退化特征

本次低周反复加载试验采用位移加载进行控制，随着反复加载次数和加载位移的不断增加，当材料屈服后，试件的刚度不断退化。刚度退化[13]一般有以下3种定义：1) 定义刚度随着反复加载次数和加载位移接近极限值而减少为刚度退化；2) 定义在保持相同的峰值荷载时，峰值位移随反复加载次数增加而增加为刚度退化；3) 定义在位移幅值不变的条件下，结构或试件的刚度随反复加载的次数增加而降低的特性为刚度退化。本文选用第一种刚度退化定义来研究试件的刚度退化现象。为定量衡量试件的刚度退化，采用割线刚度来描述反复荷载作用下试件的刚度退化现象：

式中，K为割线刚度；V为第级加载时，本级反复加载的峰值荷载；δ为第级加载时，本级反复加载的峰值荷载所对应的位移。

为研究轴压比、柱顶弯矩、腹板宽厚比0/w等因素对试件刚度退化的影响规律，图2所示为腹板厚10 mm(0/w=33.4)，8 mm(0/w=41.8)，6 mm(0/w=55.7)试件的无量纲化割线刚度的变化曲线。其中，第I类长柱试件绕截面弱轴的长细比约为140，第II类短柱试件绕截面弱轴的长细比约为60。图2中竖轴为割线刚度K与K的比值，K为柱顶水平加载位移δ=δ时对应的割线刚度，δ为试件边缘纤维发生屈服时对应的柱顶水平加载位移，为柱顶初弯矩与横截面塑性弯矩的比值。

(a) 腹板厚度tw=10 mm，h0/tw=33.4；(b) 腹板厚度tw=8 mm，h0/tw=41.8；(c) 腹板厚度tw=6 mm，h0/tw=55.7

由图2可得：试件I-A1-2与试件I-B3-1的轴压比均小于0.1，两者的柱顶弯矩相差1.1倍，两者K/K曲线几乎重合；试件I-A2与试件I-B2的轴压比均小于0.1，两者的柱顶弯矩相差1.4倍，两者K/K曲线相差不大。表明当轴压比小于0.1时，柱顶弯矩对构件刚度退化现象的影响较小。

比较同组试件割线刚度的退化趋势可知：轴压比越大的试件，刚度退化越快，刚度退化现象越明显。如图2(a)中，试件II-A1和II-B1比试件I-A1-2和I-B3-1的轴压比大，前2个试件的割线刚度变化曲线较陡，刚度退化较快。

由图2(c)可见：当/δ＜2时，各试件K/K曲线的斜率相差较大；当/δ＞2时，各试件K/K曲线的斜率趋于相同。对于腹板宽厚比较大的构件，腹板宽厚比是影响构件刚度退化的主要因素，构件轴压比对刚度退化的影响变小。

对于腹板宽厚比较小的构件，柱顶轴压比是影响构件刚度退化的主要因素，但随着腹板宽厚比的增大，腹板宽厚比对构件刚度退化的影响不断增大，而柱顶轴压比对构件刚度退化的影响不断减小。

1.2 强度退化特征

柱顶反复水平位移加载过程中，在位移幅值不变的条件下，试件承载力随反复加载次数的增加而降低的特性称为强度退化[13]。为了反映每级反复加载时构件强度退化现象，采用同级强度退化系数λ来描述强度退化现象：

式中：λ为强度退化系数；为第级加载、第次反复加载时的峰值荷载；为第级加载、第1次加载时的峰值荷载。

为研究轴压比、柱顶弯矩、腹板宽厚比等因素对试件强度退化的影响规律，图3所示为腹板厚10 mm(0/w=33.4)，8 mm(0/w=41.8)和6 mm(0/w=55.7) 试件的强度退化系数λ随柱顶水平位移的变化曲线。图3中，正向为与柱顶初弯矩作用效应相反的柱顶推力方向，反向为与柱顶初弯矩作用效应一致的柱顶拉力方向。

(a) 腹板厚度tw=10 mm，h0/tw=33.4；(b) 腹板厚度tw=8 mm，h0/tw=41.8；(c) 腹板厚度tw=6 mm，h0/tw=55.7

由图3可知：对于腹板厚10mm(0/w=33.4)的试件，当柱顶水平位移与构件边缘纤维屈服且位移的比值/δ≥5时，构件的强度退化才比较明显；对于腹板厚8 mm(0/w=41.8)的试件，当/δ≥4时，构件的强度退化开始明显；对于腹板厚6 mm(0/w=55.7)的试件，当/δ≥2时，构件的强度退化已开始明显。表明腹板宽厚比越大，构件强度退化出现得越早。

由图3(a)可知：试件的柱顶弯矩相差较小，轴压力相差数倍，但各试件的强度退化系数λ的变化曲线基本相同。表明腹板宽厚比是影响构件强度退化的主要因素，柱顶荷载对强度退化的影响较小。

2 有限元分析

采用ANSYS软件建立考虑材料非线性、几何非线性、几何初始缺陷、残余应力影响的有限元模型，对16根箱形钢柱的低周反复加载试验进行模拟分析。有限元模拟结果与实验结果的对比情况参见文献[11]。在此基础上，设计了85个数值分析构件的基本参数，部分数值分析构件的设计参数如表1所示。其中绕截面弱轴的长细比λ分别取40，50，60，80，100和120，腹板宽厚比0/w分别取33，38，42，48，52，58，65，70和75，轴压比/(Af)分别取0.05，0.1，0.2，0.3和0.4，柱顶弯矩与截面塑性弯矩比值0/P分别取0.1，0.2，0.3，0.4和0.5。

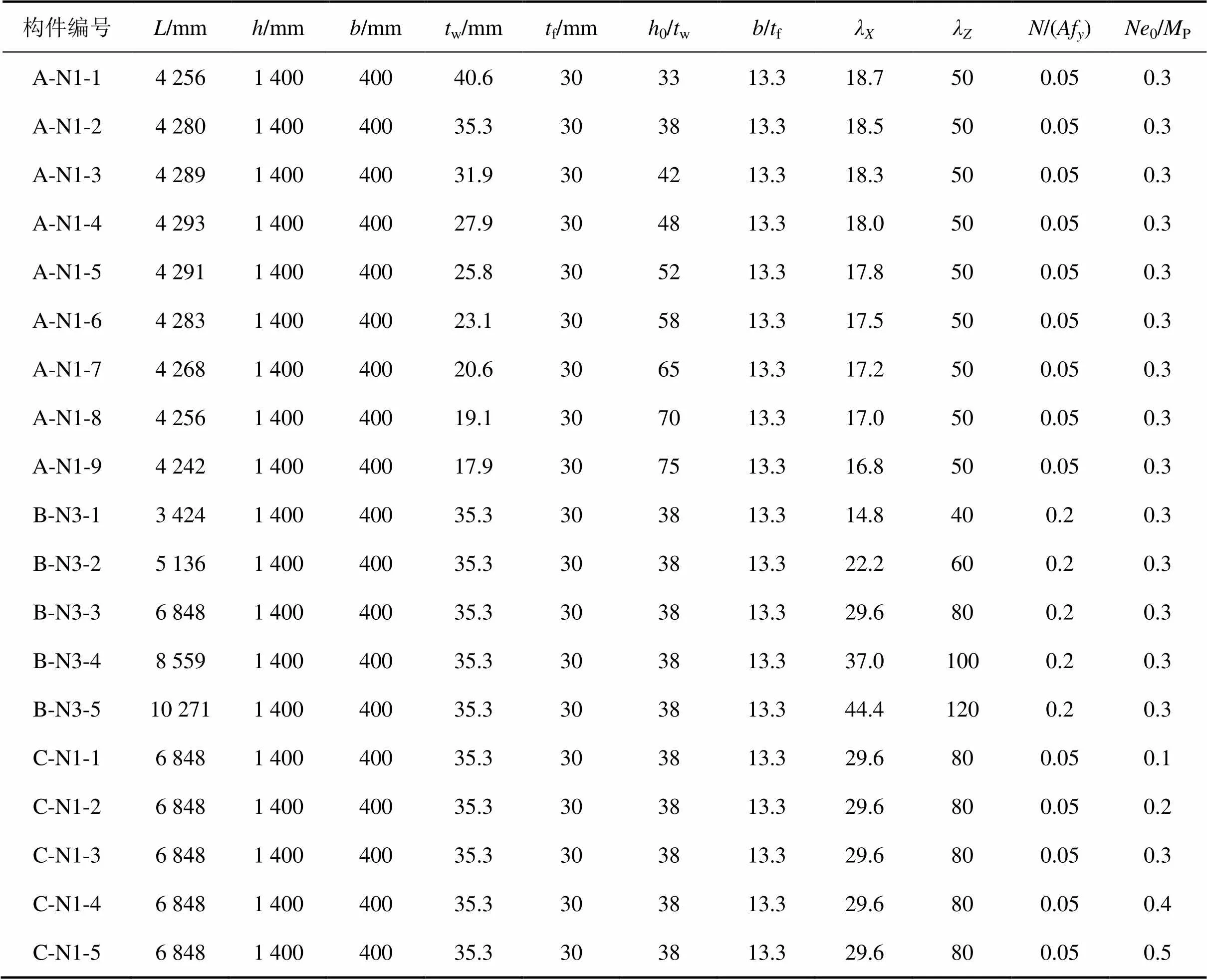
表1 部分数值分析构件的设计参数

注：λ为绕截面强轴长细比；λ为绕截面弱轴长细比；为试件横截面面积；f为箱形截面的翼缘板厚度；f为材料屈服强度；0为轴力；为偏心距；塑性弯矩P=(0.5w02+f0)f。

选取构件A-N1-6、B-N3-2、B-N3-3作为典型受力特征的代表构件进行比较分析。图4~6所示分别为3个构件的柱顶水平荷载−位移曲线、构件破坏形态及应力分布图。

(a) 荷载−位移曲线；(b) 构件破坏形态

(a) 荷载−位移曲线；(b) 构件破坏形态

由图4~6可知：构件A-N1-6经历了明显的承载力退化过程，腹板、翼缘板在柱根部位置发生了局部屈曲，构件破坏时最大Von-mises应力达345 MPa，塑性发展十分充分，构件的延性很好；构件B-N3-2经历了较为明显的承载力退化过程，腹板、翼缘板在柱根部位置也发生了局部屈曲，构件破坏时最大Von-mises应力达295 MPa，塑性发展较为充分，构件的延性较好；构件B-N3-3没有经历明显的承载力退化过程，壁板也没有发生局部屈曲，但构件发生了整体失稳破坏；构件破坏时最大Von-mises应力仅达到屈服应力235 MPa，最大应力的分布范围较广，构件的塑性发展不充分，构件的延性较差。

3 受力特征分类

综合分析16根箱形试件及85个数值计算构件的刚度退化特征、强度退化特征、荷载−位移变化曲线、破坏形态、应力分布规律等，得出反复荷载作用下，箱形压弯钢柱的3类主要受力特征如下：

1) 第1类，局部屈曲起控制作用。当轴压比≤0.1或绕截面弱轴长细比≤40时，壁板局部屈曲对构件的受力性能起控制作用，腹板宽厚比0/t对构件的延性、承载力退化、刚度退化均起主要作用。当腹板宽厚比较小时，反复荷载作用下构件局部屈曲发生较晚，塑性发展充分，承载力退化缓慢，构件的延性较好。当腹板宽厚比较大时，构件局部屈曲发生较早，承载力、刚度退化加快，构件的延性变差。对于轴压比＞0.1的此类构件，轴压比对构件受力性能的影响较为显著，轴压比越大，局部屈曲发生的越早，塑性发展越不充分，构件的延性越差。

2) 第2类，局部屈曲和整体失稳相互作用。此类构件的受力性能介于第1类和第3类构件受力性能之间，壁板局部屈曲和整体失稳对构件的受力性能均有较大影响。在反复荷载作用下，此类构件发生局部屈曲，经历明显的承载力退化过程。轴压比、腹板宽厚比、长细比、柱顶弯矩对构件的塑性发展程度、延性、承载力退化等受力性能均有较大影响，且影响是相互关联的。对于长细比较大的第2类构件，当轴压比较大时，构件整体失稳对受力性能影响最大，其受力性能接近于第3类构件的受力性能。对于长细比较小的第2类构件，壁板局部屈曲对构件受力性能的影响最大，其受力性能接近于第1类构件的受力性能。

3) 第3类，整体失稳起控制作用。当轴压比≥0.2且绕截面弱轴长细比≥80时，构件整体失稳对其受力性能起控制作用。轴压比和长细比对此类构件受力性能的影响均非常显著。在反复荷载作用下，此类构件并不发生局部屈曲，塑性发展也不充分，且不经历明显的承载力退化过程，构件的延性较差。此类构件很难达到截面塑性弯矩P。

4 稳定承载力简化计算公式

试验研究及有限元程序分析的复杂性和不易直接用于构件承载力的估算，本文根据反复荷载作用下箱形压弯钢柱的受力特点，并参考《钢结构稳定理论与设计》等[14]相关文献中关于压弯构件轴力、弯矩相关关系，构造出反复荷载作用下箱形压弯钢柱的稳定承载力计算公式如下

引入欧拉力E以考虑构件长细比对稳定承载力的影响，且由于轴力对构件稳定承载力影响较大，在式(3)中轴力与欧拉力比值构造为2幂方的关系，变量1，2，3均为腹板宽厚比h/w的函数，和分别为计算构件段范围内的最大轴压力、最大弯矩。应用优化软件1stOpt的非线性、多变量、隐函数求解等相关模块，对试验数据及有限元计算结果进行统计分析，回归出稳定承载力计算式(3)中变量1，2和3的拟合公式。

反复荷载作用下箱形压弯钢柱的稳定承载力计算公式与试验数据的相关系数[15]高达0.92，表明本文构件稳定承载力简化公式的计算精度较高。

5 结论

1) 反复荷载作用下箱形压弯钢柱的受力特征可分为3类，分别为局部屈曲起控制作用、局部屈曲和整体失稳相互作用、整体失稳起控制作用。

2) 当轴压比≤0.1或绕截面弱轴长细比≤40时，壁板局部屈曲对构件的受力性能起控制作用，腹板宽厚比对构件的延性、承载力退化、刚度退化均起主要作用。

3) 当轴压比≥0.2且绕截面弱轴长细比≥80时，构件整体失稳对其受力性能起控制作用，轴压比和长细比对构件受力性能的影响均非常显著。在反复荷载作用下，构件并不发生局部屈曲，塑性发展也不充分，且不经历明显的承载力退化过程，构件的延性较差。此类构件很难达到截面塑性弯矩。

4) 对试验数据及有限元计算结果进行统计分析，回归出反复荷载作用下箱形压弯钢柱稳定承载力的拟合公式。

[1] 刘涛, 郭彦林. 焊接箱形截面稳定承载力的直接强度设计法[J]. 工业建筑, 2009, 39(9): 36−40.
LIU Tao, GUO Yanlin. Direct strength method of welded box-section for predicting ultimate load-carrying capacity[J]. Industrial Construction, 2009, 39(9): 36−40.

[2] SU Minzhou, GU Qiang, SHEN Lin. The cyclic behaviors of box-section steel beam-columns experiment & numerical comparison[J]. Advanced Steel Construction, 2006, 2(2): 161−171.

[3] SU Minzhou, GU Qiang. Experimental and Numerical Analysis on Steel box-section beam-columns under cyclic bending[J]. Advances in Steel Structures, 2005, 1: 209−214.

[4] WANG Yanbo, LI Guoqing, CHEN Suwen. The assessment of residual stresses in welded high strength steel box sections[J]. Journal of Constructional Steel Research, 2012, 76: 93−96.

[5] 李国强, 闫晓雷, 陈素文. Q460高强钢焊接箱形压弯构件极限承载力试验研究[J]. 土木工程学报, 2012, 45(8): 67−73.
LI Guoqiang, YAN Xiaolei, CHEN Suwen. Experimental study on the ultimate bearing capacity of welded box-section columns using Q460 high strength steel in bending and axial compression[J]. China Civil Engineering Journal, 2012, 45(8): 67−73.

[6] 李国强, 王彦博, 陈素文, 等. Q460高强钢焊接箱形柱轴心受压极限承载力参数分析[J]. 建筑结构学报, 2011, 32(11): 149−155.
LI Guoqiang, WANG Yanbo, CHEN Suwen, et al. Parametric analysis of ultimate bearing capacity of Q460 high strength steel welded box columns under axial compression[J]. Journal of Building Structures, 2011, 32(11): 149−155.

[7] 施刚, 邓椿森, 班慧勇, 等. 高强度钢材箱形柱滞回性能试验研究[J]. 建筑结构学报, 2012, 33(3): 1−7.
SHI Gang, DENG Chunsen, BAN Huiyong, et al. Experimental study on hysteretic behavior of high strength steel box-section columns[J]. Journal of Building Structures, 2012, 33(3): 1−7.

[8] Ge H B, Susantha K A S, Satake Y, Usami T. Seismic demand predictions of concrete-filled steel box columns[J]. Engineering Structures, 2003, 25(3): 337−345.

[9] Osman T C, Shozo N, Kazuo T. Ultimate strain of stiffened steel box sections under bending moment and axial force fluctuations[J]. Engineering Structures, 2009, 31(3): 778−787.

[10] Osman T C, Shozo N, Kazuo T. Bending behavior of short steel cylinders under axial force fluctuations[J]. Engineering Structures, 2008, 30(3): 595−604.

[11] 李海锋, 罗永峰, 李德章, 等. 箱形钢柱受力性能分析及抗震设计建议[J]. 建筑结构学报, 2013, 34(1): 93−100.
LI Haifeng, LUO Yongfeng, LI Dezhang, et al. Mechanical behavior and seismic design suggestions of steel box column[J]. Journal of Building Structures, 2013, 34(1): 93−100.

[12] 罗永峰, 李海锋, 李德章, 等. 反复水平荷载下常偏压箱形钢柱抗震性能试验[J]. 同济大学学报(自然科学版), 2012, 40(3): 344−352.
LUO Yongfeng, LI Haifeng, LI Dezhang, et al. Experimental study on seismic behavior of eccentrically constant-compressed steel box column under cyclically lateral loading[J]. Journal of Tongji University (Natural Science), 2012, 40(3): 344−352.

[13] 罗金辉. 形钢管混凝土柱-H型钢梁框架节点抗震性能研究[D]. 上海: 同济大学建筑工程系, 2011.
LUO Jinhui. Study on Seismic Behavior of Connections between Concrete-filled L-shaped Steel Tubular Columns and H-shaped Steel Beams[D]. Shanghai: Tongji University. Department of Building Engineering, 2011.

[14] 陈骥. 钢结构稳定理论与设计[M]. 北京: 科学出版社, 2008: 67−113.
CHEN Ji. Stability of steel structures theory and design[M]. Beijing: Science Press, 2008: 67−113.

[15] 张世强, 吕杰能, 蒋峥, 等. 关于相关系数的探讨[J]. 数学的实践与认识, 2009, 39(19): 102−107.
ZHANG Shiqiang, LÜ Jieneng, JIANG Zheng, et al. Discussion about the correlation coefficient[J]. Mathematics in Practice and Theory, 2009, 39(19): 102−107.

Mechanical behavior of steel box beam-columns under cyclically lateral loading

LI Haifeng1, 2, LUO Yongfeng3, LI Dezhang4, DING Dayi5

(1. College of Civil Engineering, Huaqiao University, Xiamen 361021, China;2. Key Laboratory for Structural Engineering and Disaster Prevention of Fujian Province, Xiamen 361021, China;3. Departments of Building Engineering, Tongji University, Shanghai 200092, China;4. Hefei Administrative Bureau of Key Engineering Project, Hefei 230001, China;5. China Wuzhou Engineering Design Group Co. Ltd., Beijing 100053, China)

The degradation characteristics of stiffness and strength, load-displacement curves, failure shape and stress distribution of 16 steel box columns and 85 numerical calculated members were investigated. The interactive mechanism between local buckling and overall instability of steel box beam-columns under cyclically lateral loading was also discussed. Based on the regressive results of experimental and numerical data, the formula of stability bearing capacity of steel box beam-columns under cyclically lateral loading was fitted. The results show that when the axial compression ratio of steel box column is less than 0.1 or the maximum slenderness ratio is less than 40, the local buckling of plate has dominated effect on the mechanical behavior of steel box columns. The width-to-thickness ratio of web plate has main effect on the ductility and the degradation characteristics of stiffness and strength of the columns. While the axial compression ratio of steel box column is more than 0.2 and the maximum slenderness ratio is more than 80, the overall instability has dominated effect on the mechanical behavior of steel box columns. The effects of axial compression ratio and slenderness ratio on the mechanical behavior of the columns are both conspicuous.

steel box column; pseudo-static experiment; finite element simulation; interactive buckling; stability bearing capacity

TU391

A

1672−7207(2015)02−0676−08

2014−03−30；

2014−06−23

国家自然科学基金资助项目(51408240)，福建省教育厅科研资助项目(JA13015)(Project (51408240) supported by the National Natural Science Foundation of China; Project (JA13015) supported by the Science and Technology Program of Fujian Provincial Education Department)

李海锋，博士，讲师，从事大跨度空间结构抗震性能研究；E-mail：lihai_feng@126.com

10.11817/j.issn.1672-7207.2015.02.041

(编辑 赵俊)