摇臂转向架式星球车地形估计方法

李楠++高海波++丁亮++郭军龙++王文涛++邓宗全

摘要：针对摇臂转向架式星球车，提出一种基于摇臂转向架式星球车悬架运动学信息的星球车通过区域地形估计方法.通过分析星球车悬架正逆运动学模型，提出星球车通过区域地形估计模型.本地形估计模型将车体姿态和摇臂转角信息作为状态输入变量，可获得星球车车轮与车体相对位置，从而估计出车轮下方地形.相对于用双目相机和激光雷达地形感知方法，本方法通过车体悬架运动学信息估计地形，具有能耗低，消耗计算资源少等优点，并搭建了星球车运动学Matlab仿真平台，在多种典型工况下，验证了该方法的有效性，

关键词：星球探测平；星球探测车；地形估计；运动学

DOI： 10.15938/j.jhust.2015.03.005

中图分类号：TP242.3

文献标志码：A

文章编号：1007-2683 （2015）03-0024-05

0 引 言

在星球表面探测中，星球车用来完成对星球表面地形地貌的实地勘察、环境观测以及携带相应的科学实验仪器执行其它的探测任务.但是星球车在星球地面执行探测任务过程中，需要实时感知地形信息，以便对星球车进行运动控制和运动规划.地形感知信息是否准确，将关系到星球车运行的速度和安全，对车体控制的实时性、鲁棒性具有决定性作用.

目前，星球车对地形进行探测主要通过双目立体视觉建立数字高程图.该方法通过图像处理算法对两幅图像中相同的点进行匹配，获得地形上点相对于车体的空间坐标来估计地形.该方法可以获得较大范围的地形图像和高程信息，但该方受光照影响较大.并且需要通过复杂的图像处理算法对地形进行重构，处理数据时间较长，会消耗大量车载计算机的资源.

通过激光雷达对地面进行扫描也可以获得三维地形信息.该方法使用激光雷达和云台，通过激光测距原理测量地面与车体的相对位置.由于该方法使用主动光（发出激光）进行探测，所以该方法受光照影响较小，但发射激光需要消耗较大能量，星球车需要太阳能电池板供电，功率有一定限制，所以该方法不适合星球车使用.

本文提出了一种在星球车运动过程中通过感知车体悬架姿态来估计星球车通过区域地形方法，相比于其他星球车地形感知方法，基于星球车摇臂姿态的地形估计方法能够根据星球车车体姿态和摇臂转角信息，估计出已通过区域地形状况，车体姿态和摇臂转角信息是星球车运动控制的必要反馈变量，可以通过陀螺仪和角度传感器进行采集，所以本方法不需要额外增加专用设备就可以估计已通过区域地形信息，本方法具有能耗低，消耗计算资源少，可靠性高等优点.

1 星球车的地形估计模型建立

1.1 坐标系的建立与定义

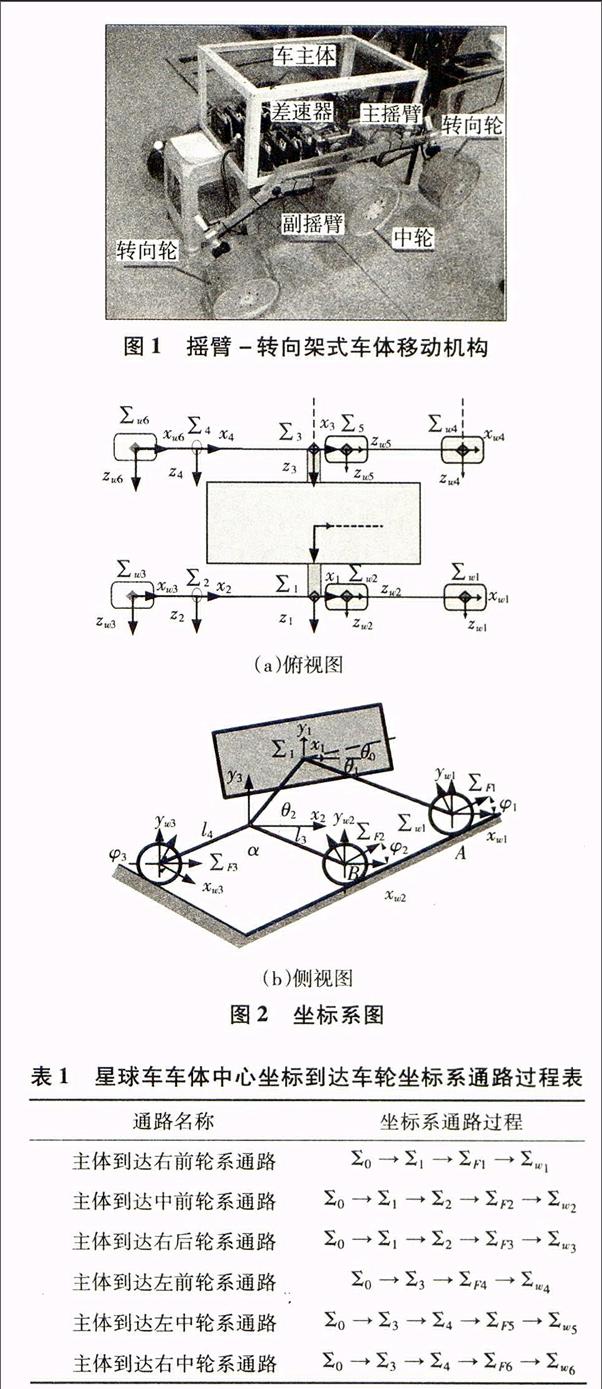
所研究的六轮探测机器人的移动机构即为摇臂一转向架式的结构，摇臂一转向架式移动机构最初是美国国家航空航天局NASA的喷气动力试验室JPL提出的，摇臂一转向架式六轮探测机器人如图l所示，主要由转向轮、中轮、主摇臂、副摇臂、差速器和车本体组成.

整个移动系统通过设置在车体内的差速器连接车体两侧的摇臂一转向架机构组成车体悬挂系统，差速器使车体的摆动幅度为左右两侧摆动角度之和的一半，如果左侧摇臂上升，右侧摇臂下降相同的角度，车体会保持不变.

建立如图2所示的六轮探测机器人坐标系，坐标系0固连在差速器.∑1原点为主摇臂右端面轴心；∑2原点为右侧副摇臂转轴轴心；坐标系∑w1 ∑w2，∑w3，∑w4，∑w5，∑W6原点分别位于右前，右中，右后，左前，左中，左后轮驱动轴中心.∑F1、∑F2、∑F3、∑F4、∑F25、∑F6原点分别位于右前，右中，右后，左前，左中，左后轮驱动轴中心，x轴方向与各车轮线速度方向相同，车体俯仰角为0。，主摇臂与车体中心夹角为 ，副摇臂与主摇臂之间的夹角为02，主摇臂支架的架杆弯角为a，副摇臂支架的架杆弯角为角 指坐标系 绕逆时针旋转至与坐标系重合所需要的最小角度，

1.2 星球车估计地形模型

由于星球车悬架是关于XI oYi平面对称结构.为简化问题，本文将在二维空间研究星球车悬架运动学问题.且星球车的主副摇臂均为刚体，可以得到车体中心坐标系到各个车轮坐标系∑wi的转换矩阵，通过转换矩阵可以得到个策论到车体中心坐标系的位置关系，从而估计出当前车轮所在区域地形信息.

坐标系y到y，的转换矩阵为：与 有关，即当 确定时，车轮相对车体中心位置具有唯一解.而车轮与地面接触，所以通过测量 估计星球车已通过区域地形信息.同理可求得另一侧的4、5、6号车轮相对车体坐标，估计另一侧已通过区域地形信息.

2 基于MATLAB的星球车运动仿真平台的建立

为验证基于悬架运动学的地形估计方法的可行性，搭建了星球车运动仿真平台.

2.1 轮地相互作用仿真

1）轮一地相互作用迭代模型

由于车轮沉陷量相对于车轮直径较小，车轮为刚性金属轮，可以认为车轮与地面之间刚体接触.无形变刚性轮在MATLAB中可以用圆表示，车轮与地面的位置关系有3种情况：相交、相切、和没有交点，其中相切和没有交点两种情况又可以分为轮子在地面之上和轮子在地面之下两种情况.车轮需要与地面接触，如图3所示，首先判断轮子与地面之间的交点个数，若为2个交点，则车轮与地面相交，车轮陷于地面之下一部分，使轮子轮心向上移动一定值；若交点个数为1个，则轮子方程与地面方程相切，轮子正常行驶与路面之上，轮子轮心不向上或者向下移动；若交点个数为0个，则轮子方程与地面方程没有交点，轮子离开了地面，使轮子坐标向下移动一定的值，迭代进入下一周期.建立的仿真框图如图3所示.

2.1 星球车悬架运动学仿真

星球车运动学仿真主要由地形模型和运动学迭代算法组成.结合轮一地作用模型和车轮悬架约束关系，可以得出星球车整车运动学迭代模型.其程序框图如7所示.

图8和图9为整车运动通过典型地形时的仿真结果.

3 星球车地形估计模型仿真验证

3.1斜坡地形下地形估计的仿真验证

在斜坡地形上，星球车沿x轴正方向运动时，图10为星球车已通过地形的估计结果.图中黑色曲线为实际地形，红色曲线为地形的估计结果.

从图10可观察到，平地和斜坡过度处，估计地形存在着一个圆角的转角，这是由于地形函数在平地与斜坡相交处产生奇异，轮子无法接触到平地与斜坡相交处的顶点，所以在交点处轮子轨迹线形成圆角.

由于斜坡路面属于分段函数，所以在做估计地形与实际地形的线性相关度分析时，考虑将采样后的数据分成两部分，一部分为上坡前的平地部分，另外的一部分为上坡后的斜面部分.对两部分分别在origin下进行线性拟合，得到了以下结果：

如表2、3所示，在平地和斜坡路面上，地形估计结果与实际地形的残差平方较小，线性相关系数和拟合相似度较高.

3.2 对于凹凸路面的MATLAB地形估计

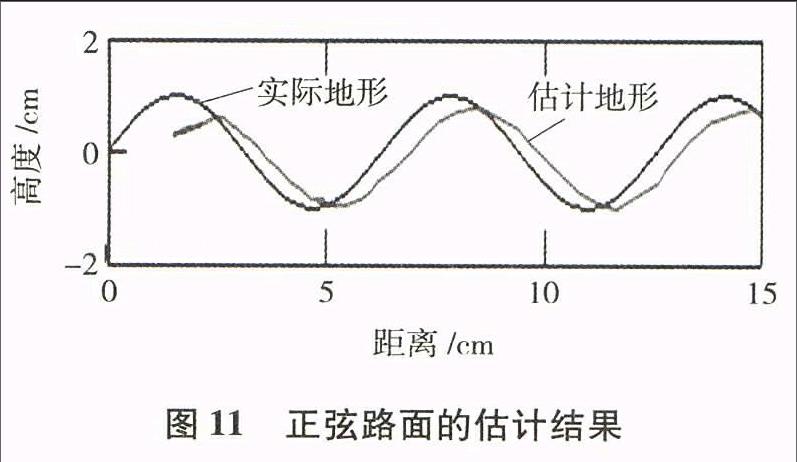
在正弦地形上，星球车沿x轴正方向运动时，图11为星球车已通过地形的估计结果，

将上述数据导人到ongm中进行线性相关性分析，得到以下结果，如表4所示：

对于连续的sm路面下估计地形与实际地形拟合度较高，但是残差平方和比较大，有一定的便宜现象.这是由于在仿真过程中没有考虑轮地接触角.轮地接触角对于地面坡度变化较敏感.在崎岖路面时，考虑轮地接触角对于估计模型的影响，并对模型进行修正.

4 结 论

本文对基于星球车悬架姿态的地形感知方法进行研究，得到了如下结论：

1）对星球车运动学进行分析，建立了基于摇臂转向架悬架的地形估计模型.

2）搭建了星球车运动学仿真平台.

3）对地形估计模型进行了仿真验证，证明了该方法的有效性，

本方法扩展了星球探测车地形探测的手段，为日后月球车、火星车等星球探测车提供了一种地形测量的新方法，经仿真验证证明该方法有效.未来工作将对该方法作一步研究，探讨轮地接触角对于地形估计的影响，并给出修正后的估计地形估计模型，以星球探测任务为导向，将本方法发展为一种可以工程化应用的新方法.