光伏组件参数拟合及输出特性研究

韩 伟，王宏华，陈 凌，吴福寿

（1.河海大学 能源与电气学院，江苏 南京 211100；2.国网浙江省电力公司检修分公司，浙江 嘉兴 314000）

0 引言

近年来，日益凸显的能源危机和环境污染，使得各国都加大了可再生能源的实施与推广，其中，基于太阳能资源的光伏发电技术以其独特的发电特性取得了广泛的发展与应用[1]。

光伏组件输出功率的大小由入射光照强度和工作温度等因素所决定[2]。通常情况下，光伏组件的制造厂商仅提供标准测试条件STC（Standard Testing Conditions）下的一条U-I特性曲线。而在工程实际中，组件很少工作在STC下，因此获知组件在不同工作条件下的输出特性就显得十分必要，同时这也是光伏组件仿真分析始终追求的目标。

经过长期的实践检验证明，光伏组件的直流物理机制模型以组件内部的电路结构研究为基础，在工程应用上具有较高的准确性[3]。该模型是一个包含多个未知参数的复杂非线性模型，然而光伏组件制造厂商的数据手册中不提供这些参数值，需要通过实际测量才能获取。因此，可根据现场装置采集的光伏组件运行数据，提取出能够准确表征实际工况的组件各模型参数。

由于光伏组件具有强烈的非线性输出特性，其模型确定和参数辨识一直是个亟待解决的难题[4]。国内外已对光伏组件仿真建模展开了大量研究，并取得了一些研究成果。常用光伏组件的等效电路数学模型主要包括双二极管模型和单二极管模型。文献[5]提出将二极管并联线性独立的电流源，组成理想的光伏电池模型，但该模型不考虑实际的串、并联电池后光伏组件的输出情况，实用性较差。鉴于数学模型存在未知参数较多、超越方程的求解复杂等问题，文献[6-7]提出忽略串联电阻或近似并联电阻无穷大的方法，简化等效模型方程个数，从而通过数值方法获取其余未知参数的准确值，但实际光伏组件中串、并联电阻值与上述假设并不完全一致。文献[8]通过求取等效电阻的方法构建光伏组件的仿真模型，然而该方法缺少必要的理论支撑。文献[9]根据光伏生产厂家所提供的STC下的实验数据，通过牛顿-拉夫逊迭代计算，即可得到相应的模型参数，但是该方法中所使用的实验数据与实际工况下的光伏组件数据存在差异，导致方法失效。

近年来，有学者将遗传算法GA（Genetic Algorithm）、粒子群优化 PSO（Particle Swarm Optimization）算法和神经网络NN（Neural Network）算法等智能优化算法引入光伏组件的参数辨识和优化中，利用迭代减小误差从而得到参数的最优辨识值[10-14]。尽管这些方法的辨识误差相对较小，但GA优化时间较长且易陷入局部最优；PSO算法的参数辨识精度有所提高，但优化时间依然较长。总而言之，利用智能优化算法的参数辨识方法虽然相对于数学分析参数近似求解的方法在精度和可靠性方面有明显的优势，但大部分传统优化算法仍有容易陷入早熟和优化时间长等缺点。人工鱼群算法AFSA（Artificial Fish Swarm Algorithm）是近年国内兴起的一种群智能算法，它通过仿生模拟鱼群的觅食、群聚、追尾行为达到搜索最优解的目的[15]。该算法具有对初值和参数选择不敏感、鲁棒性强等特点，能够较好地克服局部最优，具有良好的全局搜索能力。同时，将其与Nelder-Mead方法[16]相结合形成改进人工鱼群算法IAFSA（Improved AFSA）应用于光伏组件模型参数辨识中，增强了算法在全局搜索与局部搜索的平衡性，降低了算法的迭代次数，进一步提高了参数辨识的准确性和可靠性。因此，本文通过IAFSA最小化目标函数，使得光伏组件仿真模型输出与实际系统输出误差达到最小，从而求解出光伏组件模型各参数。

此外，光伏组件的输出特性是随光照强度、环境温度和组件参数等不断变化的非线性函数，因此要准确地模拟出实际光伏组件的输出U-I特性，必须事先获知模型各参数随光照和温度的变化关系。本文首先由多组不同工况下的U-I特性曲线提取出该组件对应的5个模型参数值，再通过最小二乘法对模型各参数随光照强度和温度对应的经验表达式进行拟合修正，在此基础上可预测出任意工况下的模型各参数值及其输出特性曲线；最后，通过其中2种工况下实验数据与仿真输出的对比验证，证明了该方法的正确性和有效性。

1 光伏组件数学模型及目标函数

1.1 光伏组件数学模型的提出

光伏电池单体的数学模型主要包括双二极管模型和单二极管模型[10]。为降低计算复杂度，同时有效兼顾计算精度和复杂程度两者之间的平衡，在实际应用中单二极管等效模型更易被广泛使用，本文即选用该模型进行研究，其等效电路模型如图1所示[17]。

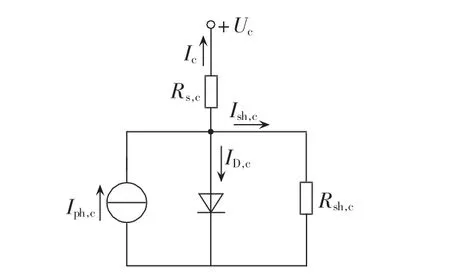
图1 单二极管等效电路模型Fig.1 Equivalent circuit model with single diode

由图1可知，在STC下该模型主要包括：光生电流 Iphref，c、二极管电流 IDref，c、二极管反向饱和电流ISDref，c、二极管理想品质因数 nref，c以及等效串 /并联电阻 Rsref，c和 Rshref，c。

根据图1所示的等效电路，可写出如式（1）所示的KCL方程：

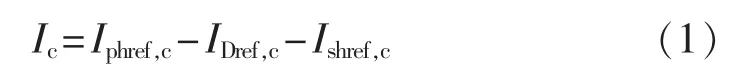
同时，肖克利方程给出了流过PN结的电流与端电压的关系，因而单二极管电流方程可表示为：

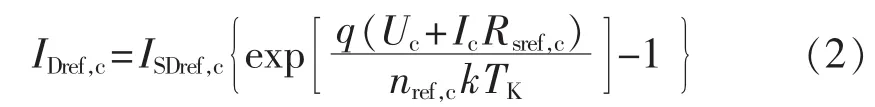
其中，q为电子电荷量，q=1.602×10-19C；k为玻尔兹曼常数，k=1.381×10-23J/K；TK为热力学温度（常温近似为300 K）。

并联漏电阻中流过的电流可表示为式（3）：

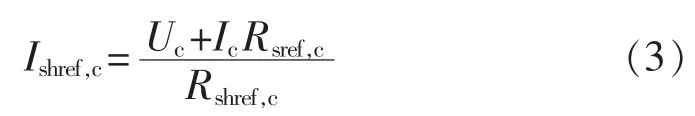
将式（2）、（3）代入式（1）中，光伏电池单体的终端电流方程可改写成式（4）：

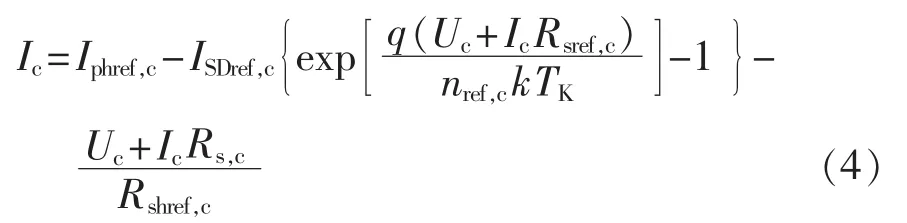
通常用户所使用的光伏发电装置并非单个的光伏电池单元，而是由多个光伏电池单元串、并联而形成的光伏组件，生产厂家所提供的实验数据也仅针对光伏组件。因此，假设光伏组件由Np个并联光伏电池组成，而每条光伏支路含有Ns个光伏电池单元串联，则实际光伏组件的KCL方程如下：

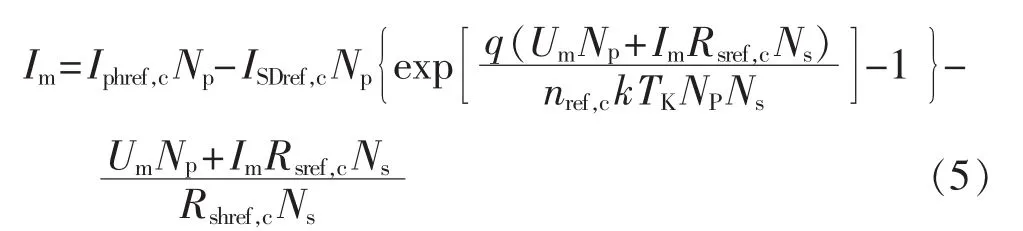
其中，Im和Um分别为光伏组件的输出电流、电压。

省略Im和Um的下标，将式（5）改写如下：

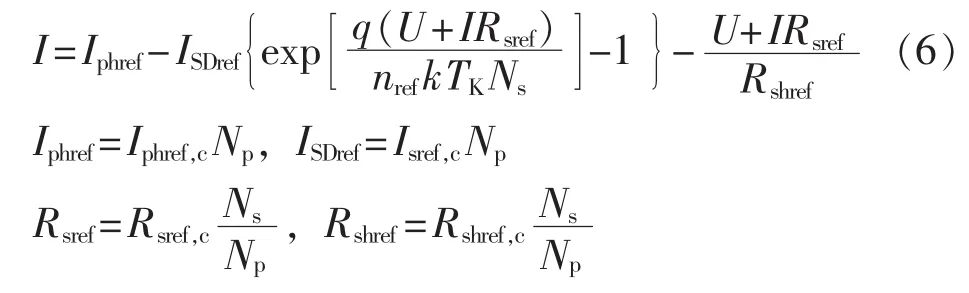
将式（4）与式（6）对比可知：光伏电池单元与组件的U-I输出特性方程形式上基本一致，唯一区别在于，式（6）中的指数项分母含有串联光伏电池单元数Ns，而该参数可以在光伏组件的用户手册中读取。因此，光伏组件的等效电路仍采用图1表示，只需对各变量下标稍作修改即可。

由式（6）可知，该方程中含有5个未知参数，分别为 Iphref、ISDref、Rsref、Rshref和 nref，而生产厂家的数据手册一般不会提供上述参数值。

工程实际中光伏组件很少工作在STC下，因此仅依靠组件生产厂商提供的STC下的一条U-I输出特性曲线获知光伏组件在STC下的基准参数值，结合经验公式进而准确模拟出任意工况下的输出特性[18]。通常，可根据如下传统参数变换关系式得到光伏组件在任意工况下的各参数值：

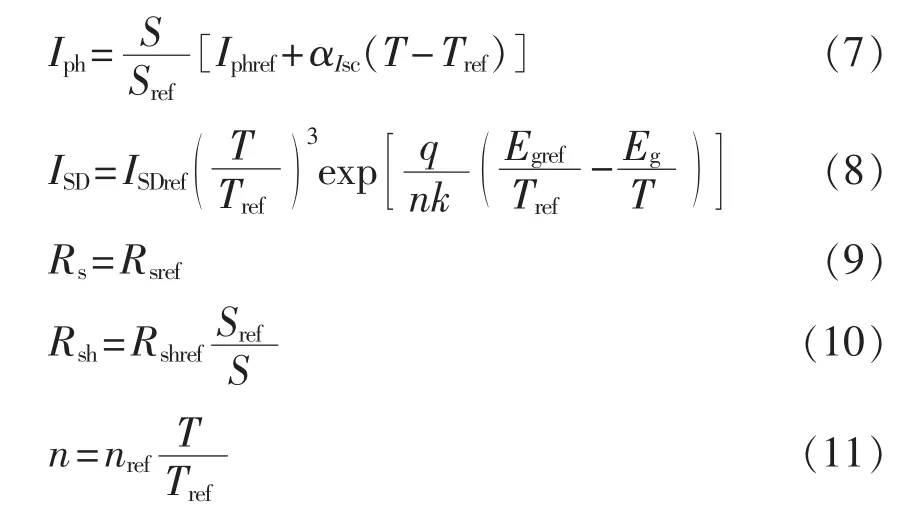
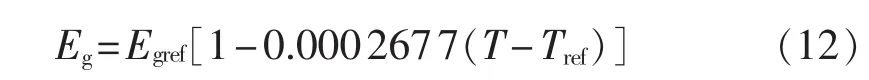
其中，S为当前光照强度；Sref为光照强度基准参考值，其值常取 1000 W/m2；αIsc为电流温度系数，其值常取0.0025；Eg为材料的能带宽度，对于硅电池而言，Tref=25℃时其能带宽度基准值Egref=1.121 eV。

将STC下的各参数值代入式（7）—（12），即可求出当前工况下的各参数值，进一步代入式（6）求解可预测出当前工况下光伏组件的输出电流值。

1.2 目标函数的建立

显然由式（6）可知，光伏组件的理论模型是一个具有隐式且非线性的超越方程，直接进行函数求解相对困难。目前较多采用数值法、解析法和曲线拟合法等，但上述方法均存在缺陷。本文基于光伏组件的数学模型特点并结合智能算法的优越性，提出通过IAFSA来提取该模型中的未知参数。在进行IAFSA求解光伏组件模型参数之前，需建立恰当的目标函数。对式（6）作如下变形：

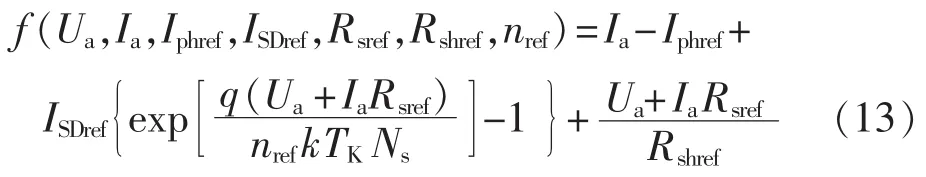
其中，Ua、Ia分别为任意一组U-I实测曲线中的电压、电流采样值。

实际上，光伏组件参数辨识问题可以归纳为一个优化问题，它的基本思想是通过最小化目标函数以求取参数最优值。本文中光伏组件模型已确定，Iphref、ISDref、Rsref、Rshref和 nref是需要辨识的参数，通过最小化实测值和仿真模型输出值之间的误差，使得模型输出尽可能地吻合实测采样值，从而所得的辨识参数值也就逼近于对应工况下的真实参数值。

本文选取的目标函数为均方根误差（RMSE）指标：

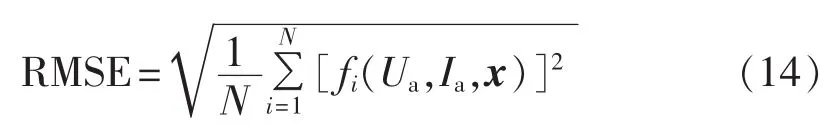
其中，x= （Iphref，ISDref，Rsref，Rshref，nref）为待求解的参数；fi（Ua，Ia，x）为第 i组实测值和仿真模型输出的差值。因而光伏组件参数辨识问题就归结为一个常规的优化问题，即求解min RMSE。

图2即为光伏组件的参数辨识策略。首先模型初始化一组参数值x，针对相同的实测采样值，模型仿真输出结果与现场实测值均输入误差估计环节以计算目标函数RMSE值；随后通过IAFSA，根据RMSE值的大小更新x，以校正仿真模型的输出值。循环执行上述辨识过程，直至RMSE值达到最小后，即可辨识出最优化模型参数值x。

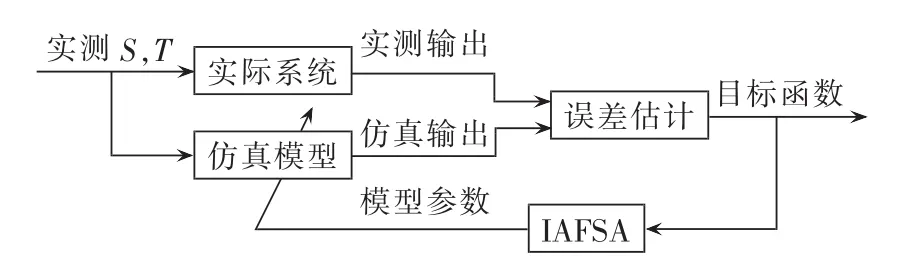
图2 光伏组件参数辨识策略Fig.2 Strategy of PV module parameter identification

2 IAFSA

2.1 AFSA

AFSA模拟自然界中鱼的集群觅食行为，采用了自下而上的寻优模式，通过鱼群中个体之间的协作使群体达到最优选择的目的[19-20]。每条人工鱼探索自身当前所处的环境，选择执行其中的一种行为算子，通过不断调整个体的位置，最终集结在食物密度较大的区域周围，取得全局最优值。

如图3所示，一条虚拟人工鱼的当前位置为X，其感知范围为V，位置XV为其在某时刻的视点所在的位置，如果该位置的食物浓度高于当前位置，则考虑向该位置方向前进一步，即到达位置Xnext；如果位置XV不比当前位置食物浓度更高，则继续巡视感知范围内的其他位置。巡视的次数Tn越多，则对感知范围内的状态了解越全面，从而对周围的环境有一个整体认知，这有助于其作出相应的判断和决策。当然，对于状态多或无限状态的环境也不必全部遍历，允许一定的不确定性对于摆脱局部最优从而寻找全局最优是有帮助的。

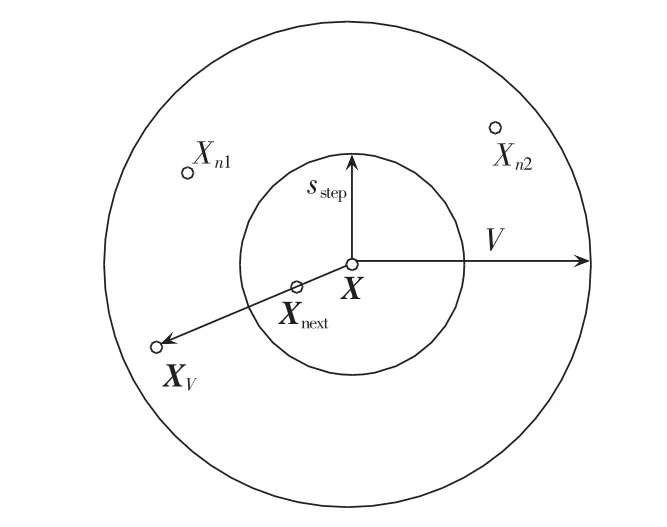
图3 人工鱼的感知范围和移动步长Fig.3 Visual scope and moving step of artificial fish

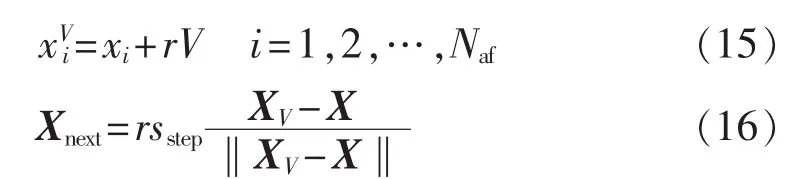
其中，r为[-1，1]区间内的随机数；sstep为人工鱼每次移动的最大步长，合理的步长设置关系到算法的收敛性。

算法中的觅食行为奠定了算法收敛的基础，聚群行为增强了算法收敛的稳定性和全局性，追尾行为增强了算法收敛的快速性和全局性。人工鱼通过对环境的感知来自主协调搜索机制，该算法最终能寻优到全局最优值附近，从而使优化问题求解。

2.2 Nelder-Mead方法描述

Nelder-Mead方法也称下山单纯形法，不同于线性规划的单纯形法，它用于求 m 元函数 f（y1，y2，…，ym）的无约束最小值。该方法由Nelder和Mead于1965年发现，故该方法又简称NM法。其算法思想是在m维空间中，由m+1个顶点可以组成“最简单”的图形，叫单纯形。NM法就是先构建一个初始的，包罗给定点的单纯形（两维空间中，单纯形是三角形；三维空间中，单纯形是锥形），然后搜索的每一步中，使用可能的4种方式（反射、扩大、压缩和收缩）产生离当前单纯形比较近的点，在新的点上函数值会和单纯形各个顶点上的值比较，一般会有1个顶点被替代，产生1个新的单纯形；重复以上步骤，直至单纯形的函数值小于预设阈值。

2.3 IAFSA

AFSA具有对参数、初值和目标函数等要求低，分布并行寻优、全局收敛性好等诸多优点，但算法后期难免出现收敛速度降低等缺陷。NM法的优势在于概念简洁、无需微分，每次迭代仅需不超过2次函数求值，收敛速度快，但也存在对初始值敏感问题。

因此，本文提出先通过AFSA对目标函数进行全局搜索，获得最优解域之后转成NM法进行快速精确搜索，既提高了收敛速度，同时又提高了搜索精度。此外，NM法的引入，并未明显增加光伏组件参数辨识算法的计算复杂度。

本文所提基于IAFSA的光伏组件参数辨识流程图见图4。

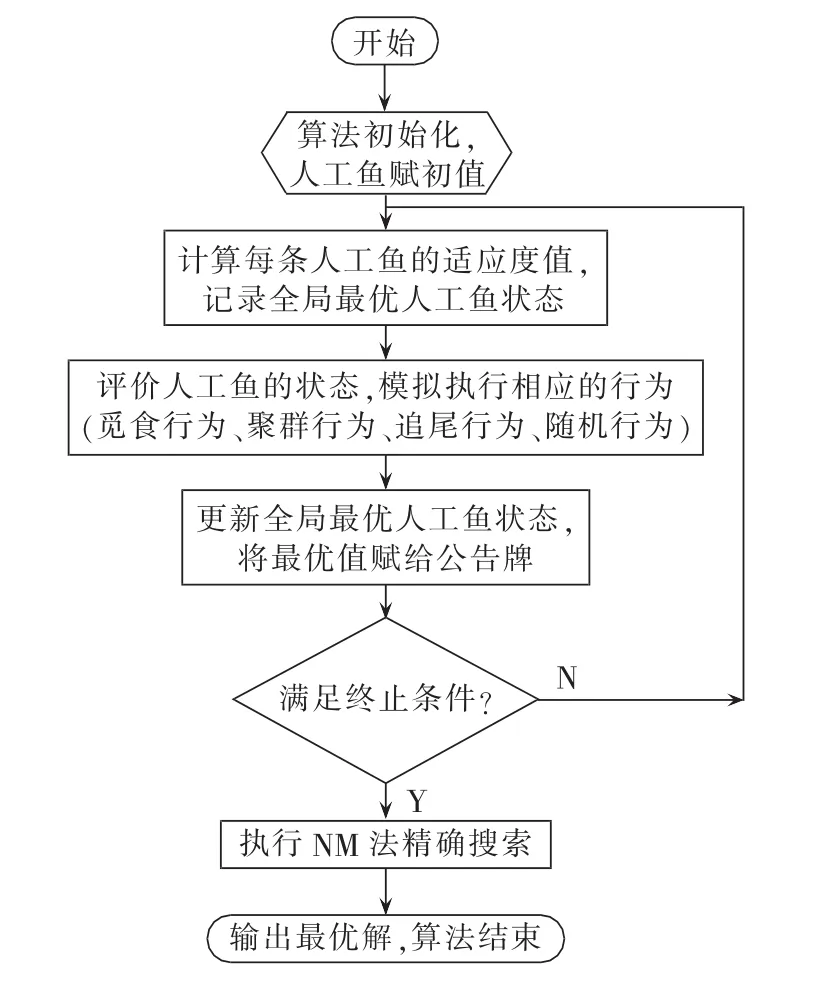
图4 改进人工鱼群算法流程图Fig.4 Flowchart of improved artificial fish swarm algorithm

3 光伏组件参数拟合及实验验证

本文应用IAFSA对任意工况下的光伏组件模型进行准确参数辨识，并利用最小二乘法对组件各参数变换公式进行拟合修正[21]。为了验证所建立的光伏组件参数拟合模型精度，本文搭建基于可编程电子负载的光伏组件户外实验平台，该装置通过电子负载等效阻抗的改变，使光伏组件工作于U-I特性曲线上不同工作点，且同步测量当前电流与电压值。利用所建立的实验平台测试采样数据，对比验证所提出的光伏组件拟合公式的精度。

3.1 组件参数辨识

文中所涉及到的AFSA主要参数如表1所示。表中，Sp为种群数目；Nmax为最大迭代次数；δ为拥挤度因子；εstop为迭代终止条件。实验选用的光伏组件类型为常州天合光能TSM-250PC05A（多晶硅，其中Ns=60），根据经验数据，其参数取值范围如表2所示。NM法以fminsearch函数的形式添加到AFSA优化过程中，其参数采用默认设置即可。

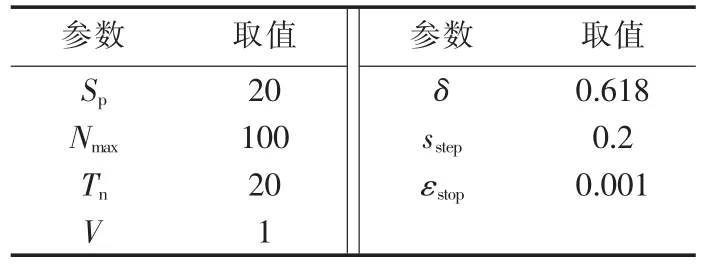
表1 参数设置Table1 Parameter settings

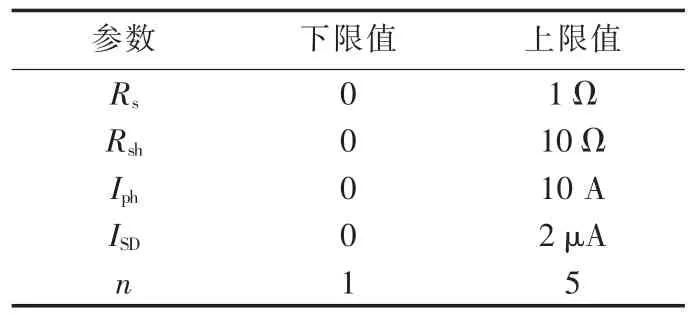
表2 光伏组件的参数上、下限Table2 Upper and lower limits of PV module parameters

PVSYST软件使用的光伏组件模型是以数学模型为基础，并通过实测对输出数据进行修正而获得的，本文通过PVSYST获取TSM-250PC05A型光伏组件在任意运行工况下的U-I特性曲线。

为了验证IAFSA辨识模型参数的精确性和快速性，对光伏组件模型在光照强度950 W/m2、温度25℃下的一组测量数据分别采用Newton法、GA、AFSA和IAFSA进行参数辨识并作对比实验，其中上述算法中各参数依据文献[22]设定。表3给出了各个算法分别运行20次后的最优辨识参数值，从表中可知，利用IAFSA得到的目标函数RMSE值最小，表明其能够获取最接近实际的模型参数值；同时该算法在参数辨识精度和计算时间上取得了较好的平衡。与此同时，IAFSA中由于引入NM法，增强了算法的全局搜索能力和局部挖掘能力，使模型参数辨识的精度和速度较AFSA有了较大的提高。

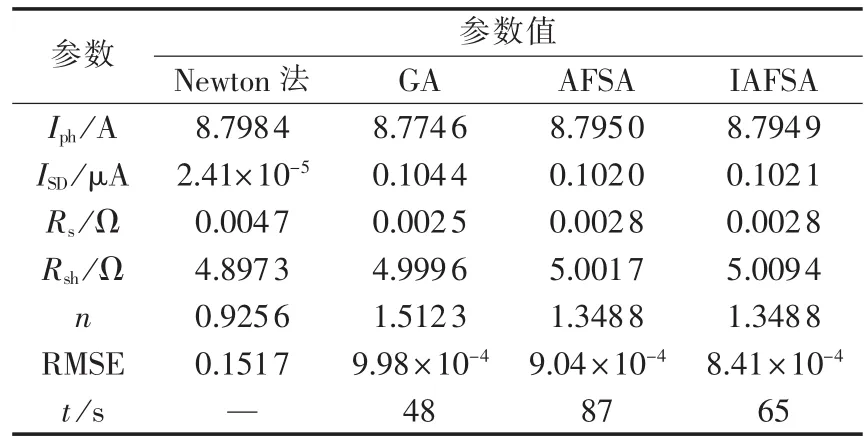
表3 不同算法辨识的光伏组件参数值Table3 PV module parameters identified by different algorithms

此外，为进一步说明IAFSA的有效性，本文对每组光伏组件的U-I特性曲线进行32个点的采样，并将其代入到IAFSA中进行模型参数辨识，选取其中4组光伏组件的参数辨识值列入表4。

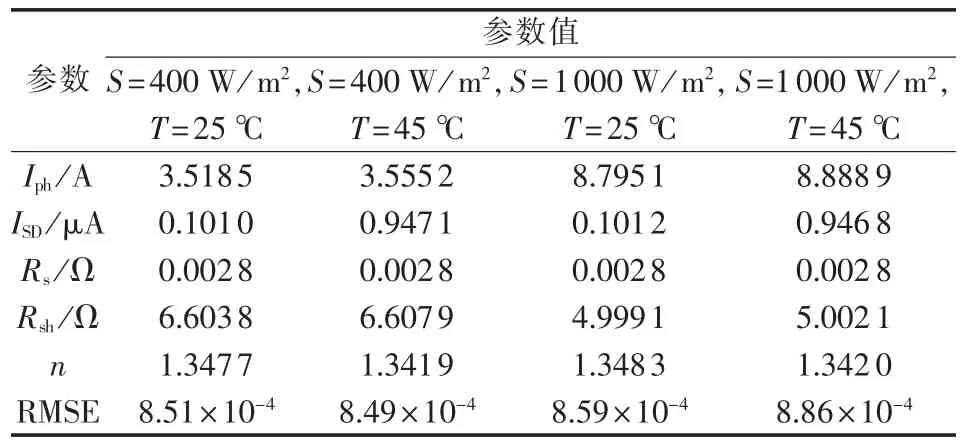
表4 4组光伏组件的参数辨识值Table4 Four groups of identified PV module parameters

由表4可知，基于IAFSA优化所得到的目标函数RMSE值均很小，说明上述参数辨识结果与光伏组件的真实参数值非常接近，能够满足光伏组件精确建模的要求。

基于上述参数辨识值，在MATLAB/Simulink环境下搭建光伏组件的五参数仿真模型。图5所示为4种不同工况下模型仿真结果与实测值的对比图，明显可知基于参数辨识所搭建的仿真模型输出较好地匹配了实测值，满足光伏组件工程建模的要求。

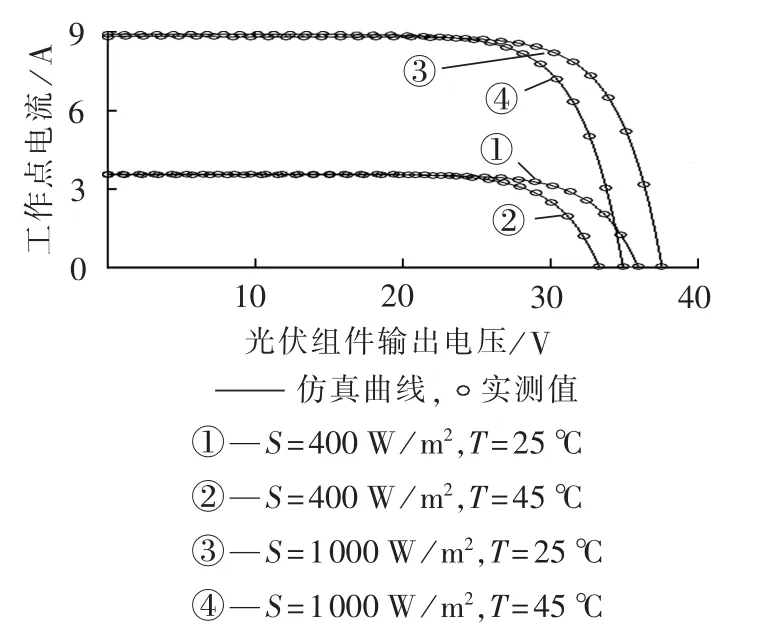
图5 光伏组件参数的仿真与实测值的对比Fig.5 Comparison between simulative and measured PV module parameters

3.2 组件参数公式拟合

此外，表4中的辨识参数值表明当光照强度和工作温度发生变化时，组件的输出特性曲线会发生变化，其参数本身也处于不断的变化中。因此，通过组件在STC（S=1000 W/m2，T=25℃）下的标准参数值，并确定各模型参数随光照强度和温度的变化关系即可准确预测出组件在各种工况下的输出特性[23]。

然而，传统的组件参数转换公式是依据不同特性曲线而确定的经验函数，对于不同材质的光伏组件均采用统一的转换公式[7，18]。由实测数据以及数学模型的计算结果可知，不同材质的光伏组件模型中参数随外界运行条件的变化而变化，但其变化趋势不尽相同，因此，对于任一实际运行的光伏组件而言，需针对其不同材质进行参数拟合，尽可能实现仿真模型输出与实测值的一致性。

同样以TSM-250PC05A型光伏组件为例，假定工作条件为：S取值100～1000 W/m2，T取值15～60℃。其中，光照强度的取值间隔为100 W/m2，温度的取值间隔为5℃，则共计100组不同的运行工况。针对每一种工况通过IAFSA进行参数辨识并将其进行描点，得到各参数的三维图如图6—10所示。

由图6可知，光生电流Iph近似地随光照强度呈现线性变化，它对光伏组件U-I特性有着最为显著和直接的影响。通过最小二乘法对其进行拟合，得到Iph的近似拟合表达式为：

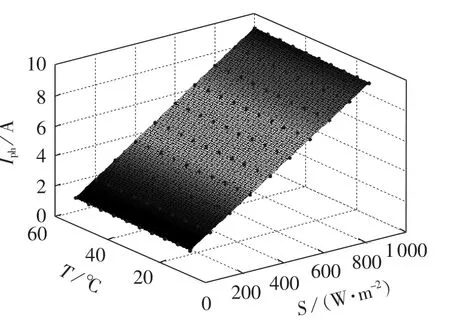
图6 参数Iph随光照和温度的变化趋势Fig.6 Variation of Iphalong with radiation and module temperature

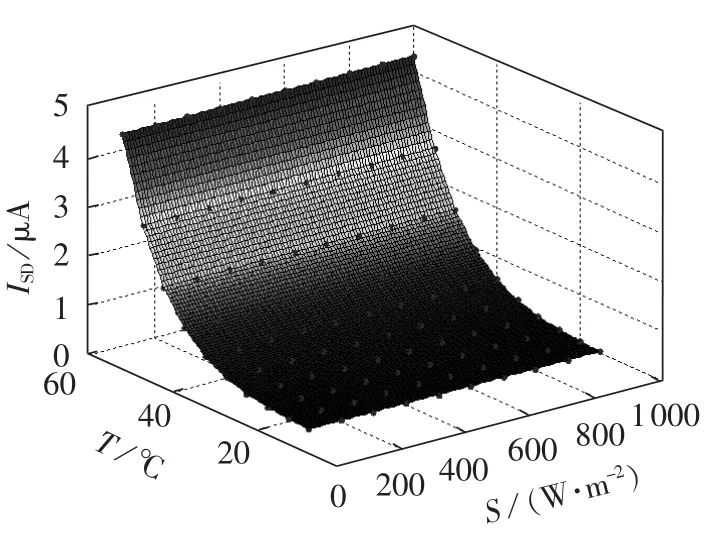
图7 参数ISD随光照和温度的变化趋势Fig.7 Variation of ISDalong with radiation and module temperature

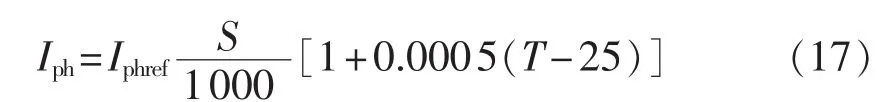
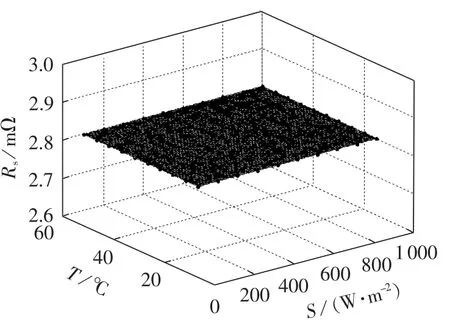
图8 参数Rs随光照和温度的变化趋势Fig.8 Variation of Rsalong with radiation and module temperature

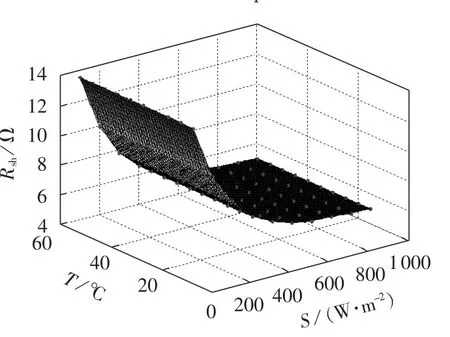
图9 参数Rsh随光照和温度的变化趋势Fig.9 Variation of Rshalong with radiation and module temperature

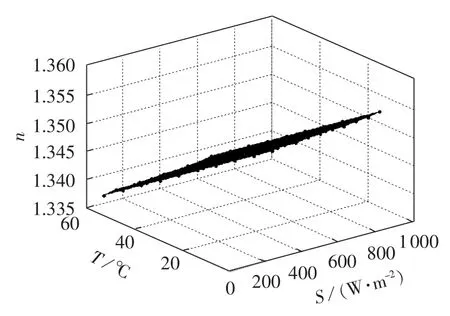
图10 参数n随光照和温度的变化趋势Fig.10 Variation of n along with radiation and module temperature

由图7可知，二极管反向饱和电流ISD随温度变化明显，该参数影响光伏组件的输出电压。通过最小二乘法对其进行拟合，得到ISD的近似拟合表达式为：

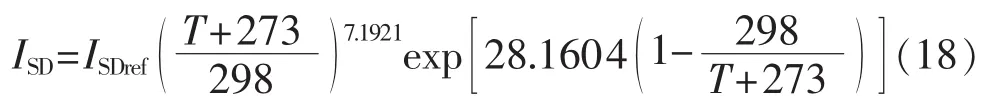
理论上，串联电阻Rs影响光伏组件最大功率点附近的U-I曲线形状。由图8可知，Rs在不同的工况下变化不明显，基本上呈现为一恒定数值。通过最小二乘法对其进行拟合，得到Rs的近似拟合表达式与式（7）基本一致。

并联电阻Rsh则对光伏组件U-I曲线中短路点附近的斜率有影响，Rsh数值越大，则曲线在短路点附近越平行于横轴。由图9可知，并联电阻Rsh随入射光照强度会发生变化。通过最小二乘法对其进行拟合，得到Rsh的近似拟合表达式为：

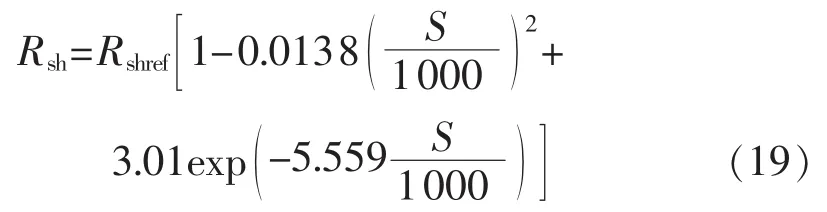
二极管理想因子n对组件的输出电压有较大影响。由图10可知，n随温度会发生变化，通过最小二乘法对其进行拟合，得到n的近似拟合表达式为：

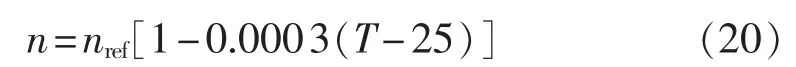
在确定光伏组件的实际工作条件后，通过上述组件参数随光照和温度的变化关系式即可获取当前工况下的各参数值，从而进行光伏组件建模与分析。

3.3 组件输出特性实验验证

基于上述理论分析，搭建光伏组件户外实验平台，平台采用TSM-250PC05A型组件。在实际运行工况下，通过日射强度计TBQ-2和温度传感器Pt100对当前光照强度和环境温度分别进行测量，需要注意的是，为了尽可能真实反映光伏组件的当前工作温度，该温度传感器安放在组件的背面。

利用该实验平台对光伏组件的每条U-I特性曲线进行256个点的实测取值（等间隔选取其中30个点）。以任意2种实际运行工况为例，传感器所测数据分别为：S=425 W/m2、T=23 ℃；S=846 W/m2、T=34℃。根据当前工况值并结合表4中所示STC下辨识出的各参数参考值，分别采用2种不同的参数变换公式获得组件对应参数值，如表5所示。

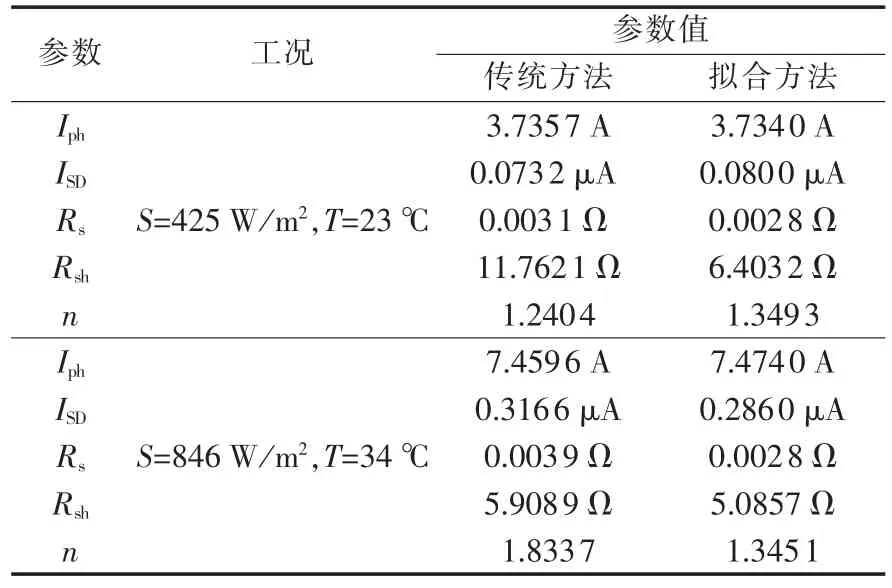
表5 2种方法获得的光伏组件参数值Table5 Two groups of PV module parameters obtained by two methods

由表5可知，通过不同方法计算的光伏组件当前参数值不尽相同，且部分参数值存在较大的误差。为更直观地表明上述各参数计算方法的准确性，将这2种方法在同一工况下的仿真结果与该组件对应的实测值分别进行对比，如图11、12所示。

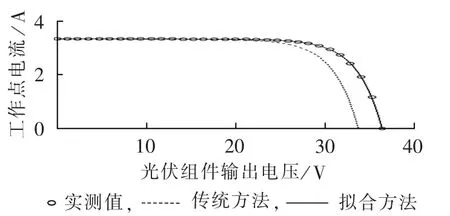
图11 采用本文方法、传统方法和实测得到的光伏组件参数对比（S=425 W/m2，T=23℃）Fig.11 Comparison of PV module parameters among proposed method，traditional method and measurement when S=425 W/m2and T=23℃

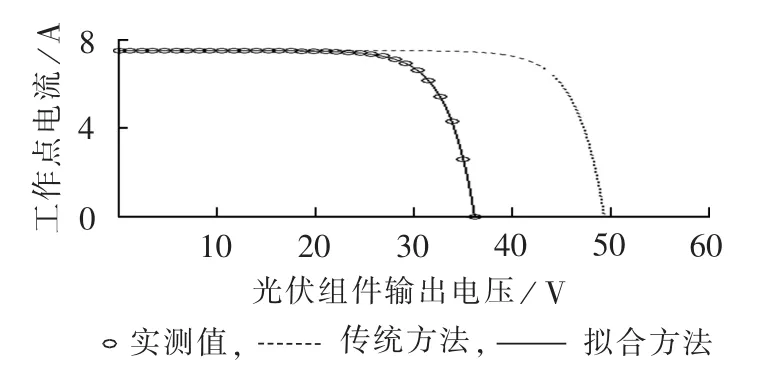
图12 采用本文方法、传统方法和实测得到的光伏组件参数对比（S=846 W/m2，T=34 ℃）Fig.12 Comparison of PV module parameters among proposed method，traditional method and measurement when S=846 W/m2and T=34℃

由图11、12可知，采用本文所提的参数拟合修正法能够准确反映当前光伏组件的参数值及输出特性，具有较高的参数辨识准确度，满足光伏组件建模与分析的精度要求；而传统公式变换法采用统一的经验变换公式，不考虑光伏组件的类型，因此必然存在较大的误差，与实测曲线吻合度较差。

综上所述，基于IAFSA和最小二乘法建立的光伏组件仿真模型，能较好地匹配实测数据值，误差值在可控范围内，户外实验数据进一步说明了本文所提的参数拟合修正法的正确性和有效性。

4 结论

本文引入IAFSA对光伏组件进行参数辨识。在对不同工况下的光伏组件输出特性曲线提取出对应模型的5个参数值，通过最小二乘法对各模型参数随光照强度和温度对应的初始经验公式重新进行拟合。该拟合修正公式相较于传统经验公式更为精确，能更好地反映出不同材质光伏组件的参数变化趋势，且通过该方法能够获得光伏组件在任意光照强度和温度下的输出特性曲线。通过2组不同工况下实验数据与仿真输出的对比验证，证明了本文所提方法的有效性和准确性。该拟合修正公式的提出有利于光伏功率预测和故障诊断等问题的进一步研究，同时具有较高的工程应用价值与推广意义。下一步的工作将重点研究不同材质光伏组件拟合公式的区别及其参数的物理意义。

致 谢

本文实验平台是在河海大学（常州校区）丁坤副教授的帮助下完成的，在此向丁坤副教授表示衷心的感谢。