一种高铁供电事故气象因素关联模型的分析方法

程宏波，何正友，王 玘，姜晓锋，母秀清

（1.西南交通大学 电气工程学院，四川 成都 610031；2.华东交通大学 电气与电子工程学院，江西 南昌 330013）

0 引言

中国已成为世界上高速铁路（简称高铁）运营里程最长、运营速度最快、在建规模最大的国家。随着越来越多的高铁投入运营，人们对高铁的关注已逐步转向如何保持高铁的安全正点运行、提高高铁的服务质量、改善乘客的出行体验上，提高高铁的运营和服务质量已成为一个实际而又迫切的问题。

牵引供电系统是高铁列车的动力来源，一旦出现故障将会导致高铁列车失电停运，造成列车晚点，影响旅客的正常出行，给铁路部门的声誉带来不良的社会影响。引发高铁牵引供电系统故障的原因是多方面的，恶劣的气象条件是诱发高铁牵引供电系统故障的一个重要因素，媒体报道的大部分高铁停电事故都和恶劣天气有关[1-5]。根据气象条件对高铁牵引供电系统可能受到的影响进行预测和评估是可靠的高铁调度管理的重要内容之一。

当前对高铁牵引供电系统设备状态的评估大多基于设备本身的监测信息，未考虑外部气象环境对牵引供电系统状态的影响[6-7]。文献[8]运用系统致灾理论对人为因素、设备因素、环境因素、管理因素的危机征兆进行了考察和研究，总结了铁路交通灾害的致灾风险及成因规律；文献[9]则对泥石流对铁路运输造成的危害进行了风险评估并提出防治的措施；文献[10-11]在对恶劣天气进行建模的基础上，对考虑恶劣天气影响的牵引供电系统风险评估的指标体系和评估方法进行了研究。这些文献多从定性的角度进行分析，得到了铁路运输受气象环境因素影响这一结论，但是未对具体的影响规律以及分析这一规律的方法进行研究。在公路交通领域，文献[12]建立了高速公路的交通事故时空分析模型，分析了影响其故障的相关因素，文献[13-15]则对智能交通愿景下的时空数据分析及融合方法进行了研究。这些方法都可为分析牵引供电系统的故障提供借鉴。

本文分析了牵引供电系统工作状态与气象因素之间的关系，确定了影响高铁牵引供电系统工作状态的气象因素，建立了高铁牵引供电系统事故起数的气象分析模型并对模型进行检验，利用建立的模型实现对高铁牵引供电系统工作状态的提前预测和预警。高铁牵引供电系统事故灾害的气象条件分析及预警对提高高铁牵引供电系统的可靠性、保证高铁的安全正点运营将会产生重要意义。

1 影响牵引供电系统安全的气象因素分析

由于牵引供电设备多为露天布置，工作状态易受外部气象环境如风、雨、雪、雷电、雾霾等的影响，而且我国的高速铁路多架设于高架桥上，牵引供电系统受各种气象条件的影响更为明显。理论上，考虑气象环境的影响因素越多越好，但根据一般性、简单性和实用性原则，本文对可能影响牵引供电系统工作状态的气象因素分析如下。

a.风速的影响。风对牵引供电系统的影响主要体现在接触网上：接触网在风的作用下可能会使线索的内力超过许用值，引起导线拉断；风引起的接触网振动会导致结构疲劳；大风引起接触网舞动影响受电弓的正常受流。风的作用强度和风速的平方成正比，因此当风速增大到超过一定程度之后，对接触网设备的影响更为突出。

b.降水的影响。降水对牵引供电系统的影响主要体现在设备绝缘性能的变化上：降水增加空气湿度，影响绝缘性能；绝缘表面的污秽受潮后易出现污闪；水流在设备表面易造成短路情况。

c.温度的影响。温度会影响牵引供电系统接触线的工作状态，温度的变化会引起接触线驰度的变化，进而对接触线的张力产生影响。

d.雷击的影响。雷击是影响牵引供电系统供电可靠性的重要因素之一。由于接触网露天架设，部分高铁线路架于高架桥上，极易受到雷击的影响。雷击接触网会产生过电压，可能引起绝缘子损坏，造成线路跳闸。同时，过电压会侵入牵引变电所，引起站内设备的损坏。

e.相对平均湿度的影响。相对平均湿度对牵引供电系统的影响与降水的影响相似，多是对设备的绝缘产生不利影响。

图1为2010—2012年某供电段牵引供电系统故障统计及该地区的气象因素的变化情况，时间按春夏秋冬4个季节的顺序排列。图中列出了风速、温度、降水量、雷击次数以及平均相对湿度的变化情况，从图中可以看到，牵引供电系统的故障与雷击次数之间的关系明显，3 a的雷击次数高峰基本对应当年的故障次数高峰；故障高峰期和温度高峰期也具有高度的一致性，两者都出现在每年的夏季；故障次数与风速、月平均降水量以及平均相对湿度之间也呈现出一定的相关性。

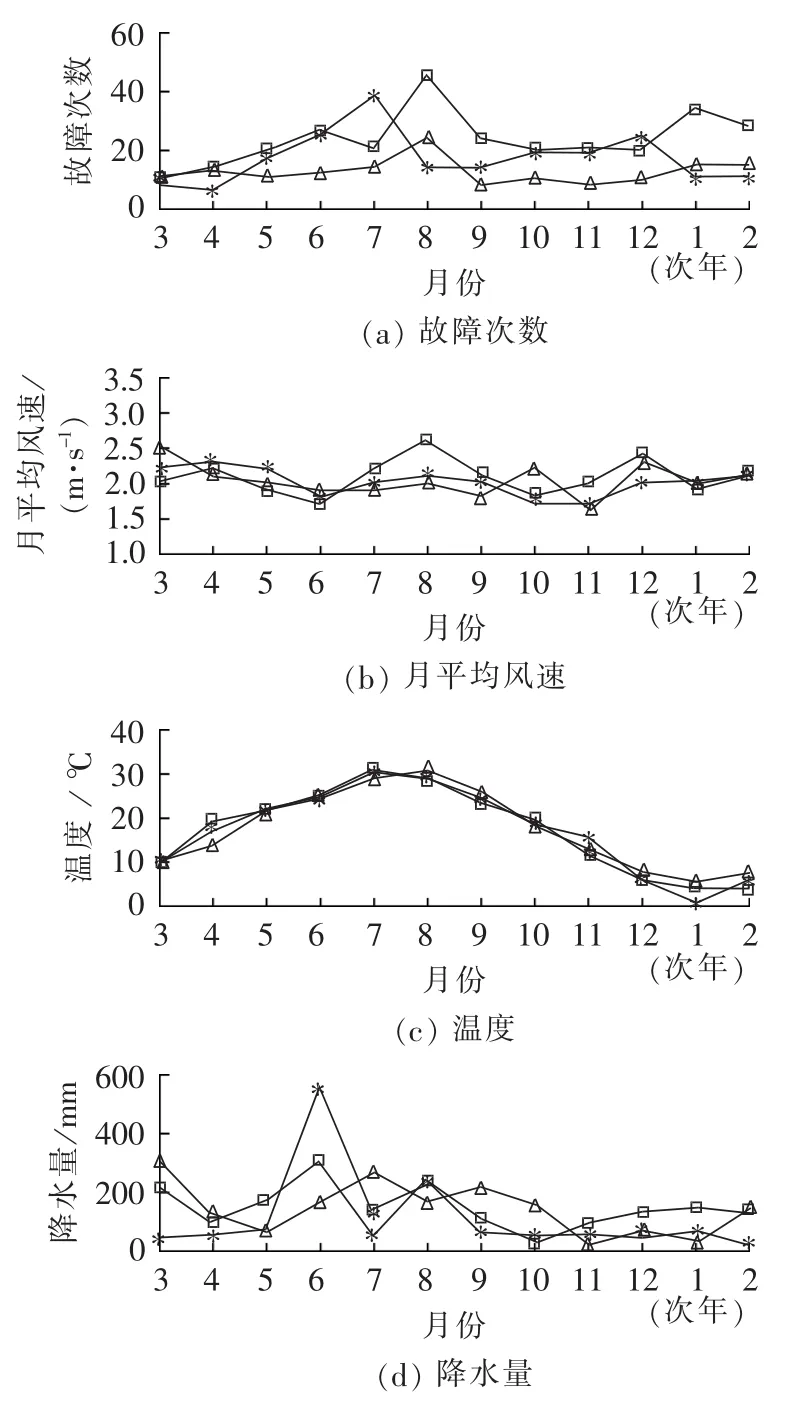
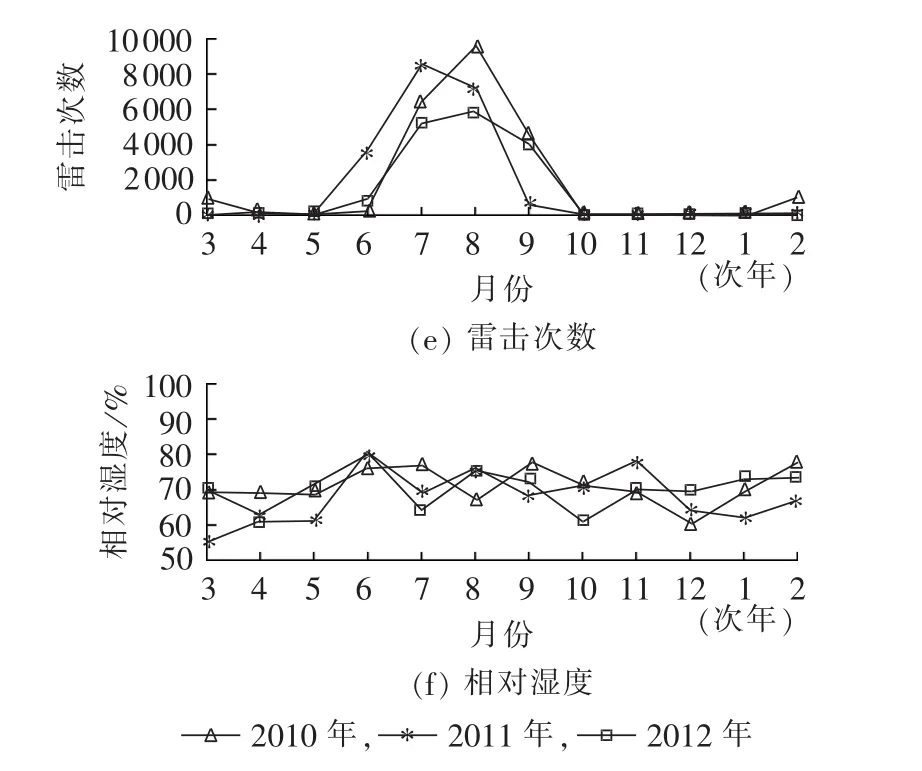
图1 某段牵引供电系统事故起数与该地区气象条件之间的关系Fig.1 Relationships between traction power supply system accident times and meteorological factors of a power supply section

相关系数可以反映出统计变量相互之间的关系密切程度，以气象因素的月平均统计值作为变量x，牵引供电系统的月事故起数作为变量y，两者之间的相关系数为：

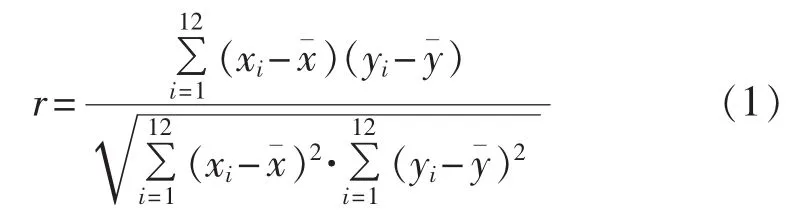
其中，xi（i=1，2，…，12）为某一气象因素在第 i个月的平均值；为该气象因素在 1a内的平均值；yi（i=1，2，…，12）为牵引供电系统在第i个月的事故起数；为该段牵引供电系统1a内的平均故障次数。

表1列出了该段牵引供电系统2010—2012年的事故起数与对应的气象条件之间的相关系数。

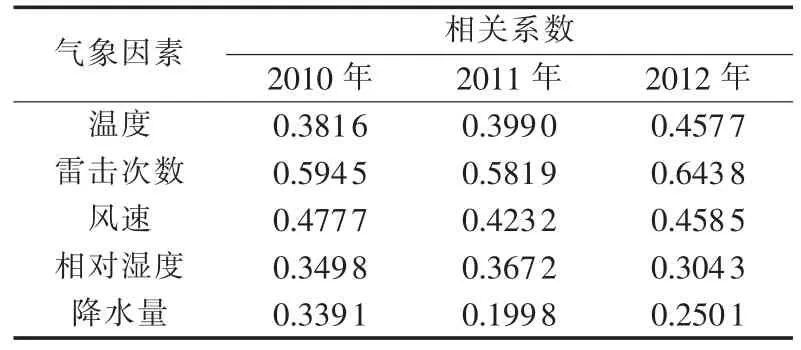
表1 某段牵引供电系统事故起数与气象条件的相关系数Table 1 Correlation coefficients between traction power supply system accident times and meteorological factors of a power supply section

从表1中可以看到，气象因素与牵引供电系统事故起数之间都呈正相关。相关程度划分为：为低度线性相关，为显著性相关，0.7≤为高度线性相关[16]。根据该划分，雷击次数、风速与牵引供电系统的事故灾害之间为显著性相关；温度与事故起数之间在2012年呈显著性相关，在2010年和2011年则呈低度线性相关；相对湿度、降水量则和牵引供电系统的事故起数之间呈低度线性相关。

相关系数表明牵引供电系统的故障次数和气象条件之间存在联系，但具体的联系关系则需做进一步的分析。

2 牵引供电系统事故的气象关联分析模型

2.1 模型变量的选元方法

从前面的分析可以看到，影响牵引供电系统工作状态的因素是多方面的，其中有些因素影响较为显著，有些因素的影响则较为轻微，如何从众多的因素中确定对牵引供电系统事故影响比较重要的因素作为气象分析模型的自变量，对于整个分析模型的确定非常重要。

在建立回归模型时，选择自变量的基本指导思想是少而精，虽然滤除部分自变量有可能导致估计量产生有偏性，但可以降低拟合偏差的方差。

逐步回归选元将变量逐个地引入，每当引入一个自变量后，对已选入的变量进行逐个检验，当原引入的变量由于后面变量的引入而变得不再显著时，将其剔除，这个过程反复进行，直至无显著的自变量加入和剔除为止。采用逐步回归法对牵引供电系统事故灾害气象分析模型的变量进行选择的基本思路如下[12]。

a.确定显著性检验最大F值及其对应的变量。利用牵引供电系统的事故起数y与气象因素xj（j=1，2，…，m；m 为参与分析的气象因素个数）分别进行回归分析，得到其显著性检验F值，若最大的F值在给定的显著性水平α=0.05下满足 F＞F0.05（1，n-2）（n为观测值的个数），那么对应的气象因素与事故起数之间存在显著的线性关系，该气象因素将首先被选中。

b.对其他变量进行偏F检验。在剩下的m-1个变量中再利用偏F检验来选择一个变量加入到模型中，偏F统计量为：

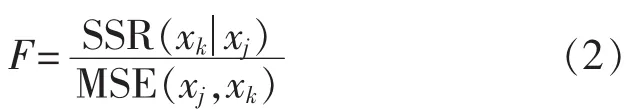
同样，若偏 F 统计量 F＞F0.05（1，n-l-1），则认为在给定的显著性水平α=0.05下线性关系是显著的，该自变量被选中。

c.针对引入变量重新进行F检验。每当引入一个自变量以后，采用F检验方法对已在模型中的每个变量重新进行显著性检验，如果检验不显著，则去掉该变量，再重复进行步骤b和c；否则保留该变量，重复进行步骤b和c。直到待选的全部变量根据给定的显著性水平，再没有一个变量能够被选入或剔除时为止。

可以看到，逐步回归选元是一个不断吐故纳新的过程，对牵引供电系统事故影响不重要的气象因素最终是不会被引入的，即使开始时被引入最后也会被剔除。

2.2 牵引供电系统事故的气象关联模型建立

在选定了影响牵引供电系统工作状态的气象因素作为变量之后，需要进一步明确牵引供电系统的事故起数与气象变量之间的具体关系，以便实际工作中能根据气象条件的变化情况来确定牵引供电系统工作状态的变化程度。其核心问题为参数的估计及评价问题。

用Y表示牵引供电系统事故灾害的统计样本，X表示气象因素的观测样本，Y关于X的总体回归模型可表示为：

用 B=[β0，β1，β2，…，βn]T表示回归系数，则回归方程可表示为：

因此，回归模型建立的关键和核心在于对回归系数B的估计，利用最小二乘估计法可得：

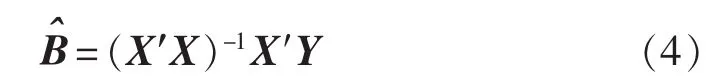
其中，X′为X的转置。

当求得各变量的回归系数 β0、β1、…、βn后，线性关联模型可写为：

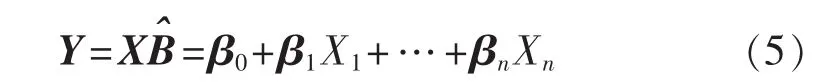
在估计出回归方程后，需要对回归模型的效果进行诊断，本文采用方程拟合优度指标R2和残差分析来反映方程拟合的好坏。拟合优度指标为：

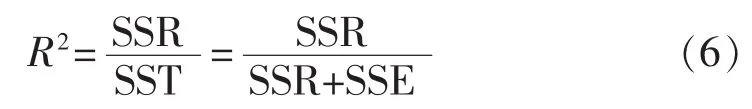
其中，回归平方和SSR反映了自变量对总离差的贡献；残差平方和SSE反映了误差项对总离差的贡献。拟合优度R2越大，表明拟合越好。

2.3 基于关联模型的牵引供电系统事故起数预测

在回归模型通过以上各种检验后，就可根据气象条件的某一个观测样本X0来对牵引供电系统的事故起数的平均值进行预测。

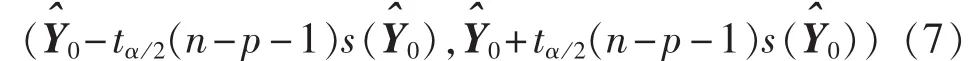
3 实例分析

以铁路某供电段2010—2012年的牵引供电系统故障为研究对象，分析该段牵引供电系统故障灾害与该地区气象条件之间的关系，建立牵引供电系统事故灾害起数与气象因素之间的关联模型。牵引供电系统的故障统计数据包括该供电段管辖下的所有牵引变电所及全部接触网的故障，气象资料来源于该地区气象局的资料统计。

将该供电段2010—2012年牵引供电系统的事故情况进行整理，分别得到牵引供电系统这3 a中每月的事故起数，将其作为因变量y；将该地区的对应气象情况进行整理，分别得到该地区这3 a中每月的月平均温度 xt、雷击次数xl、月平均降水量 xr、月平均风速xw、月平均相对湿度xh，将其记为自变量x=（xt，xl，xr，xw，xh）。 变量 y 与 x 的变化情况如前文图1中所示。

首先在不进行回归选元的情况下，直接对故障次数与气象因素的5个变量进行回归分析，得到故障次数y与气象因素之间的关系：

各项因素前的系数称为回归系数，是根据统计样本由式（4）通过最小二乘估计得到的，体现了故障次数与气象因素之间的相依程度。

回归后所得的残差区间杠杆图如图2所示。残差杠杆图显示，残差均匀分布在0点线附近，但第17组数据出现高杠杆点，说明第17组数据为异常观测点，在拟合时应予以剔除。返回的统计值中检验参数R2=0.6914，说明模型拟合得不是很好，F检验值为1.9673＞p，符合要求。但与显著性概率相关的p值为0.1824＞0.05，这说明回归方程中有些变量可以剔除。

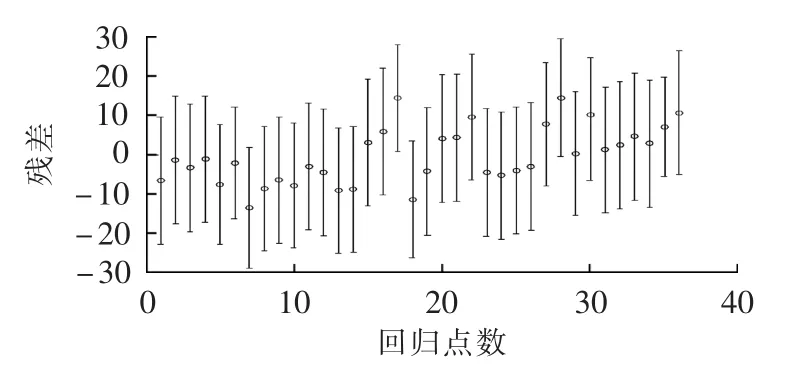
图2 回归分析所得的残差杠杆图Fig.2 Residual lever diagram by regressive analysis

进行逐步回归选元后，得到的回归方程为：

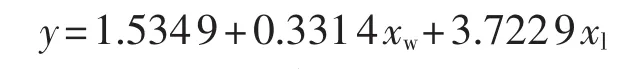
此时，回归方程中保留了原始变量xl、xw，分别为月雷击次数和月平均风速。此时模型的评估参数分别为：R2=0.8493，F 检验值为 7.4761＞p，与显著性概率相关的p值为0.027 4＜0.05。以上指标值表明回归效果比较理想。回归结果表明牵引供电系统的故障次数和雷击次数及平均风速紧密相关，这与实际情况的经验判断相一致。

从表2中的数据可以看出，对模型的变量进行选元后，回归的情况要更好，拟合优度R2进一步提高，均方根误差 RMSE（Root Mean Square Error）进一步减小，表明拟合的结果更为理想。

表2 2种回归模型的评估参数比较Table 2 Comparison of evaluation parameters between two regression models

利用选元之后的模型对该段牵引供电系统2013年3—5月的故障次数进行了预测，预测情况如表3所示。

表3 回归模型对牵引供电系统事故预测情况Table 3 Results of traction power supply system accident prediction by regression model

从表3可以看到，利用回归模型对牵引供电系统的事故起数进行预测具有一定的可行性，其95%置信区间预测能够大致反映故障发生的次数范围，但由于牵引供电系统的运行状态受多方面因素的影响，除气象条件外，还易受一些外部突发情况的影响，因而在当前样本有限的情况下，根据气象情况进行的预测较实际情况更为保守。随着智能化牵引供电技术的实施，监测的气象信息逐步丰富，积累的故障数据逐渐增多，偶发情况对统计的影响将会随着样本的增多而逐步地减小，统计和预测的结果将会更为精确，其预测结果将能为牵引供电系统的运营管理提供参考。

4 结论

牵引供电系统工作于外界自然环境中，常受到自然环境的影响，各种大风、雷雨等天气都会对牵引供电系统的状态产生较大影响。本文在分析影响牵引供电系统工作状态的各种气象因素的基础上，提出利用多元回归分析来挖掘牵引供电系统的事故起数和该地的气象条件之间的对应关系，建立事故起数和气象因素之间的回归模型，并利用该模型对故障次数进行预测。通过某段牵引供电系统事故起数和气象条件之间的回归分析结果验证了所提方法的可行性。未来，随着牵引供电系统事故样本数据的逐渐积累，回归分析的结果将更趋于准确，其预测的结果也将更接近实际。