基于实证数据和模糊控制的多时间尺度风储耦合实时滚动平抑波动

刘春燕，晁 勤，魏丽丽

（新疆大学 电气工程学院，新疆 乌鲁木齐 830047）

0 引言

以风能为原动力的风力发电系统，由风速变化引起的风电功率波动对电力系统安全性和稳定性的影响越来越受到人们关注。文献[1-3]通过内蒙古和东北风电场实际数据分析充分给予了论证，提出了建立有效的风电功率预测系统方案；但并未涉及解决风电波动的方法。随着储能技术水平不断提高，经济成本降低，在风电场出口侧安装储能装置平抑其输出功率波动[4-7]，是目前解决平抑风电波动的方法之一。文献[8-11]研究了单一储能或混合储能平抑风电功率波动的有效性与可行性。文献[12-13]提出采用正态分布和低通滤波器的方法确定平抑目标制定储能容量。文献[14]对风电场日出力曲线和储能容量关系进行了研究。文献[15-16]基于模糊控制理论和机会约束规划对混合储能进行充放电控制和容量配置。但上述文献均没有涉及多时间尺度风储耦合及储能容量配置和充放电控制策略研究。

本文提出基于某风电场出力实证数据在秒级（3 s）、分钟级（10 min）、小时级（1 h、3 h）多时间尺度上采用概率统计法研究风电波动规律和风储耦合特性，采用实时5点滚动法制定多时间尺度平抑风电波动目标，兼顾国网规定的多时间尺度风电波动限值进行目标修正，并利用储能分时跟踪平抑风电波动目标，合理确定多时间尺度储能配置容量和充放电控制策略，考虑储能经济性，采用补偿度进一步修正储能容量，并采用模糊控制原理优化荷电状态（SOC）达到不过充过放的优化控制策略。

1 基于实证数据的风电出力多时间尺度波动特性分析

1.1 风电出力间歇性及随机性论证

对某风电场（259.5MW）2011年1月1日至12月31日数据进行分析与统计，如图1所示（截取某连续4天实际出力（标幺值），时间尺度为10 min）。结果表明：风电出力具有间歇性（第1天风电出力第50个采样点至第67个采样点始终为0）和随机性（连续4天毫无规律）。

图1 某风电场连续4天的风电出力Fig.1 Wind power output of a wind farm for four successive days

风电出力在不同时间尺度（秒级（3 s）、分钟级（10 min）、小时级（1 h、3 h））呈现不同波动特征，因此，有必要分时段研究风电功率波动特征，找出平抑波动最佳方案。

1.2 多时间尺度风电出力波动特性分析及统计

1.2.1 风电出力波动分析统计方法

风电出力波动分析统计方法主要从风电出力在不同时间尺度下的变化率及幅度和分布概率角度进行，定义如下4个计算公式。

a.风电功率波动变化率ΔPb。

设 P（t+1）为当前时刻风电出力，P（t）为前一时刻的风电出力，PN为总装机容量，则ΔPb为：

b.风电功率波动幅度平均值Pavr。

设风电场某时间段风电变化功率为ΔP，n为风电场出力时间段数，则Pavr为：

c.风电功率波动变化量标准差D为：

d.风电功率波动变化率分布概率G。

设NΔPb为风电功率变化率某数值出现的次数，Ntotal为风电功率变化率出现的总次数，则G为：

1.2.2 基于实证数据的风电波动量与国网规定对比分析

国家电网规定风电波动不同时间尺度必须限制在一定范围内（简称“国网限值”，下同），如表1所示。

表1 风电场最大功率变化率国网推荐值Table 1 Maximum wind power variation recommended by State Grid

根据式（1）和式（4）以及国网限值对某区风电场（259.5 MW）实证数据进行1 min和10 min最大变化量分别大于15 MW和50 MW的概率统计，结果如表2所示。

表2 某风电场风电变化率概率统计表Table 2 Statistics of wind power variation rate of a wind farm

统计结果表明：风电波动超标率较高，需要加装储能平抑，但是国网的规定只是2个时间尺度，对不同储能装置不完全吻合其充放电特性，有必要增加超短（秒级）和超长（小时级）时间风电波动分布特性分析，以利于风储耦合研究。

1.2.3 多时间尺度风电出力波动特性分析及统计

a.单台风机与风电场输出功率对比分析。

图2为某 259.5 MW 风电场与其中某 1.5 MW单台风电机组每10 min出力（标幺值）对比图（为使图形清晰化，一年样本数据中只选择其中144个采样点）。从图中可以看出：由于风电场内各台风电机组排列方式、风速及尾流效应等因素的影响，在相同时间内，单台风电机组出力波动要比风电场出力波动大。风电场较单台风电机组输出功率波动具有“平滑效应”。因此建议大规模风机并网以风电场配置储能较宜。

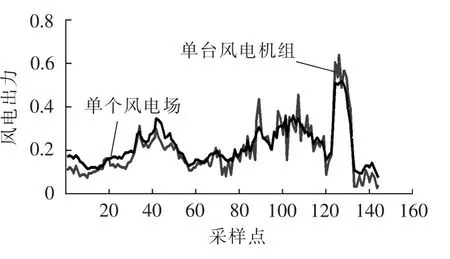
图2 单台风机、单个风电场输出功率对比Fig.2 Comparison of power output between single wind turbine and whole wind farm

b.多时间尺度风电功率变化率对比分析。

对上述同一算例系统中单台风电机组和风电场在每一时间段内实测输出功率数据进行统计分析，由于现场风电最小采集时间间隔为3 s，国网规定限值是1 min和10 min，目前已安装的大部分储能容量最大充放电时间为4 h，因此涉及的时间尺度为3 s、10 min、1 h、3 h。

在各时间尺度下，应用式（2）和（3）对单台风电机组和风电场功率波动幅度平均值和风电功率波动变化量标准差进行统计，表3为风电场统计结果。

表3 各时间尺度波动幅值和标准差Table 3 Fluctuation amplitude and standard deviation for different time scales

由表3可知，不同时间尺度风电波动特征不同。

在各时间尺度下，应用式（1）和（4）对单台风电机组和风电场功率波动变化率分布概率进行统计，如图3和图4所示（图中风电出力变化率为标幺值）。由图可知，风电出力变化率集中于0值附近，满足正态分布。

对单台风电机组和风电场输出功率变化率各个时间尺度在装机容量的20%内、[20%，40%）、[40%，90%）范围分布概率累计和最大分布概率及风电出力波动最大波动量（标幺值）进行统计，如表4和表5所示。由表可知，在短时间尺度内，风电出力变化率分布较集中。在长时间尺度，即小时级以上，风电出力变化率分布不集中。

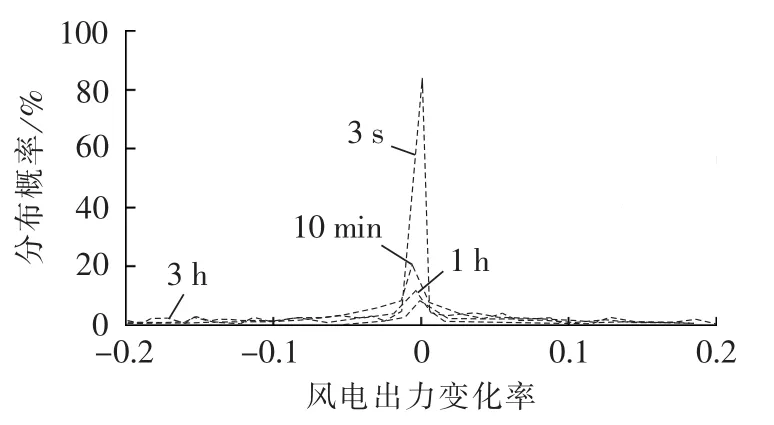
图3 多时间尺度下单台风电机组出力变化率情况Fig.3 Power output variation rate of single wind turbine for different time scales

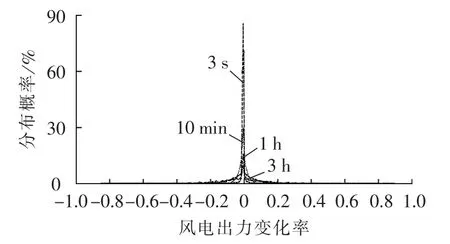
图4 多时间尺度下单个风电场出力变化率情况Fig.4 Power output variation rate of whole wind farm for different time scales

表4 各时间尺度输出功率变化率[20%，40%）、[40%，90%）概率统计Table 4 Probability of power output variation rate within [20%，40%） and within [40%，90%）for different time scales

表5 各时间尺度风电功率波动最大分布概率和最大波动量Table 5 Maximum probability and fluctuation of wind power for different time scales

由表1可知该风电场国网规定的10 min最大变化量不允许超过50／259.5=0.2即20%，1 min最大变化量不允许超过15／259.5=0.06即6%，而图4和表4均表明各时间段风电场波动变化率主要分布在装机容量的20%内，变化率在[20%，40%）的概率虽然较[40%，90%）的概率稍高但都很小，因此确定将变化率概率在[20%，40%）的波动量抑制到20%以内，虽然平抑效果不完美，但所配置的储能容量不需要很大。

下面分析算法在一段时间内对运动目标的持续跟踪定位效果.假设目标的初始位置为[50,50]Tkm，以速度[-500,-500]Tm/s运动，测量误差σ=102m，利用仿真1中的布站方式，每1秒对目标进行1次定位.不同算法对目标的跟踪定位性能如图6所示.

2 基于模糊控制的风储耦合实时滚动平抑波动储能容量及控制策略

2.1 兼顾国网限值制定风储耦合实时滚动平抑波动目标

本文运用实时采样5点滚动平均算法制定能够跟随实际风电功率变化的平抑目标曲线，再兼顾国网限值修正平抑目标曲线达到风电功率变化率在20%规定范围内。计算公式如下。

a.实时采样5点滚动平均算法求目标Pt（t）：

b.国网限值修正得到最终平抑目标值Pzt（t）：

其中，ΔPv为国网限值。

以时间尺度10 min（风电场）为例（下同），采用式（5）和式（6）对某风电场进行计算，如图5所示为平抑目标与风电实际功率（均为标幺值，后同）曲线（为清晰起见，截取图中部分数据）。根据数据显示，平抑目标在一定程度上平滑了风电实际功率波动。

图5 风电实际功率与平抑目标Fig.5 Actual wind power and smoothing target

2.2 考虑补偿度并跟踪目标构建储能容量及控制策略

2.2.1 确定储能充放电控制策略

如图6所示，当风电实际功率大于平抑目标值时，能量流向储能；当实际功率小于平抑目标时，能量从储能流出；当风电实际功率等于平抑目标时，储能不动作。

2.2.2 确定储能额定功率

由图6计算差值得到各点储能充放电功率值，但依据表5可知，最大波动量达到0.8950 p.u.，储能功率配置偏大，经济性差，本文采用概率统计法对差值功率进行概率统计，只需补偿[20%，40%）范围的波动，即确定一定补偿度后求取储能额定功率。

图6 储能充放电控制策略示意图Fig.6 Schematic diagram of energy storage charging／discharging control strategy

若储能容量选择风电场装机容量，折算标幺值为1，对图6进行储能充放电功率与充放电次数概率统计，如图7和图8所示（图中储能充放电功率为标幺值）。结果表明：储能充放电功率大部分在风电场装机容量的30%以内，完全吻合了[20%，40%）范围。当补偿度为0.9时，储能充放电功率为15%，即38.92 MW。

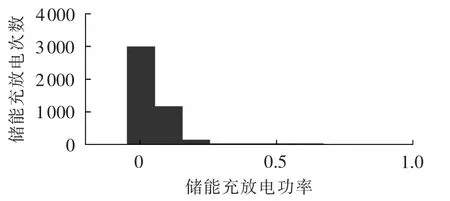
图7 储能充放电概率分布Fig.7 Probability distribution of energy storage charging／discharging

图8 储能充放电功率累计概率Fig.8 Cumulative probability of energy storage charging／discharging power

图8表明，如果接近全额补偿，储能充放电功率需要风电场装机容量的30%。

2.2.3 确定储能额定容量

对图6进行风电实际功率与平抑目标所围成的各面积概率统计计算，如图9和图10所示（图中横轴均为标幺值），储能充放电容量多数在风机装机容量的30%以内。若累计概率达到90%以上，储能额定容量为风机装机容量的20%，即51.9 MW·h。

2.3 采用模糊控制法优化SOC修正控制策略

由上述确定的储能额定容量与额定功率是建立在100%完全充放电基础上，势必造成储能过充过放，对储能造成损害。因此本文采用模糊控制法优化SOC，进一步修正控制策略，避免储能过充过放，延长储能使用寿命。

图9 储能容量概率分布Fig.9 Probability distribution of energy storage capacity

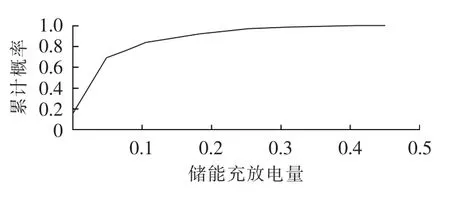
图10 储能容量累计概率Fig.10 Cumulative probability of energy storage capacity

模糊控制系统框图如图11所示。其中输入量为储能剩余SOC和储能装置充放电功率Pe，输出为储能修正功率。隶属度和模糊规则如图12和表6所示。

图11 优化SOC控制策略图Fig.11 Strategy of optimal SOC control

图12 输入、输出隶属度函数Fig.12 Input and output membership functions

表6 模糊控制规则Table 6 Fuzzy control rules

储能装置处于充电运行方式，Pe＞0：

储能装置处于放电运行方式，Pe＜0：

其中，Eoriginal为储能装置初始容量；Pe为储能装置充放电功率；ηc为充电效率；ηd为放电效率；EN为额定容量。

采用中心法求得储能修正值，得到修正后的储能功率为 P′e（t）=Pe（t）+ΔPe。

当储能剩余电量不充足时，适当减小储能放电功率，避免储能过放，反之亦然。

图13给出了有无模糊控制时剩余SOC变化情况。从图中可以看出，加模糊控制策略后，剩余SOC在0.2～0.8范围波动，避免储能装置枯竭或者饱和，在一定程度上延长使用寿命。

图13 剩余荷电状态变化Fig.13 Variation of remaining SOC

2.4 储能平抑多时间尺度风电功率波动效果分析

风储耦合平抑多时间尺度风电波动方法总体流程如图14所示，得到10 min风储合成出力（标幺值）总体效果如图15所示。

从图15中可以得出，加装储能之后，风电实际输出功率得到平抑，有多数点跟踪上平抑目标，部分采样点没有跟踪上平抑目标，是因为补偿度选取0.9和SOC优化造成，但误差不大，总体效果良好。

考虑到秒级风电出力波动变化率多数在装机容量的5%以内，只有个别风电出力变化率超出5%，满足国网1min限值6%的要求，并且平抑秒级波动可通过风电机组桨距角和变频器进行控制。所以本文主要分析分钟级和小时级风电出力变化率所需储能功率与容量。

表7给出了储能装置10 min、1 h、3 h额定功率和额定容量配置，表中单台风机1.5 MW，单个风电场259.5 MW。

根据表7计算结果得出：风电出力变化率在分钟级所需要的储能容量较小时级小。随着时间尺度增加，平抑风电出力变化率所需储能容量增加。在平抑风电出力时，考虑储能装置的响应时间和功率密度，分钟级波动可采用功率型（超级电容器）或能量型（铅酸蓄电池）储能装置，小时级波动只能采用能量型储能装置。

图14 储能平抑风电输出功率变化率流程图Fig.14 Flowchart of wind power output variation restraint with energy storage

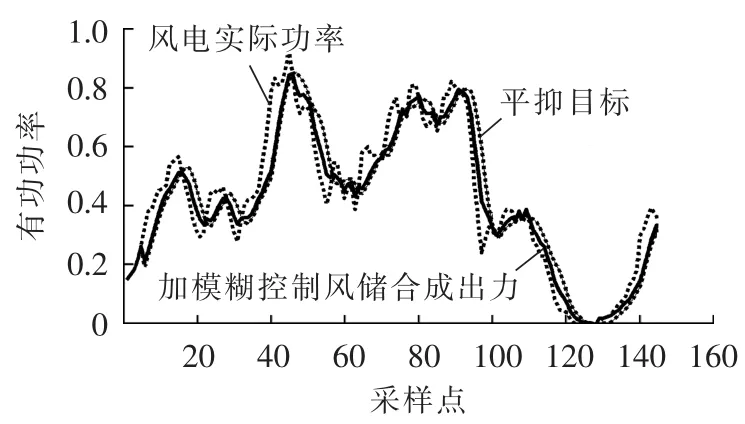
图15 风储合成总体效果Fig.15 Overall effect of wind-storage coupling

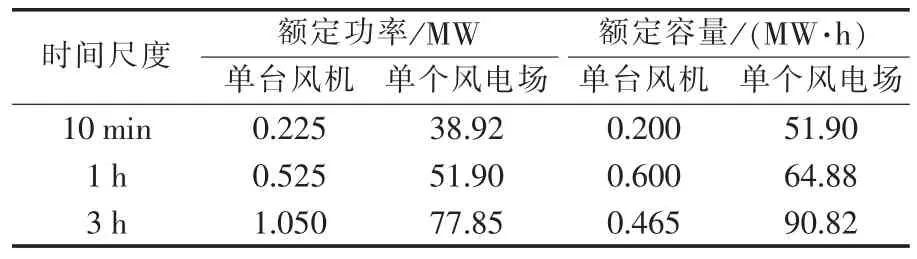
表7 不同时间尺度储能容量和功率配置Table 7 Configuration of energy storage capacity and power for different time scales

3 结论

本文基于风电出力长时间实测历史数据，对于单台风电机组和风电场输出功率在不同时间尺度下的波动特性进行了量化分析对比，制定了平抑多时间尺度风电波动的储能容量和控制策略，所得主要结论如下。

a.随着时间尺度的增加，风电输出功率变化率增加，主要分布在装机容量的20%以内。

b.考虑平抑风电输出功率所需储能的成本，采用实时采样5点滚动法兼顾国网限值制定平抑目标，基于概率分布方法和引入补偿度确定储能额定功率及额定容量。研究表明，随着时间尺度的增加，储能额定容量和额定功率也增大，但不超过风电装机容量的30%，经济性较好。

c.通过模糊控制能够更好地优化储能充放电功率，使得储能装置避免枯竭或者饱和，延长储能使用寿命。