基于特征向量法的电池储能装置最佳安装地点选择
2015-09-19杜冰心王德林
杜冰心,王德林
(西南交通大学 电气工程学院,四川 成都 610031)
0 引言
储能技术能够对电网进行能量调节和管理,实现动态功率补偿,从而极大地增强电网运行控制的主动性。电池储能因其能量密度较高、响应时间短、对场地要求低、寿命及效率相对高,且成本低廉、制造技术成熟、能够实现大规模生产等优点,广泛使用于UPS、电能质量调节、负荷的削峰填谷等方面,具有广阔的发展前景和巨大的应用潜力,是大规模储能技术的重要发展方向之一。电网运行工况确定以后,储能装置的布局将直接关系到对系统有功、无功功率的补偿效果,而且关系到储能的利用率和电网的经济效益。因此,需要选择储能装置在电网中合适的接入点,使其最大效能地改善系统的稳定性。本文采用电池储能装置(CBEST)旨在提高电力系统稳定性。目前针对电池储能在电力系统中最佳位置选择的研究甚少。考虑到电池储能在提高系统稳定性中所起的作用与FACTS装置类似,故本文参考了FACTS装置的选址方法。
国内外学者对FACTS装置在电网中接入点选择的方法进行了大量深入探讨,并取得了不少研究成果[1-8]。文献[1]中指出留数是状态矩阵可控性因子与可观性因子的乘积,其大小表征了控制器移动特定特征值的能力,故可用留数作为储能控制器有效性的衡量指标。文献[2]利用特征根变化与留数的关系确定PSS/FACTS的最佳装设地点,考虑了系统的可控性和可观测性,但忽视了FACTS装置自身控制系统对系统振荡的影响。文献[3]最早提出采用特征向量法分析发电机的振荡模态,首先求取全系统状态矩阵的特征值和特征向量,通过分析各振荡模态的特征向量,确定对该振荡模态影响最大的发电机组。文献[4-5]采用灵敏度分析法分析了超导储能装置不同安装位置对系统特征值的影响。仿真结果表明:若某节点的灵敏度越大,其有功功率和无功功率变化对整个系统的影响也越大,该节点应为功率调节设备的最佳安装地点。另外,网络损耗最小的灵敏度分析方法的基本思想是将储能装置作为一个负荷来分析,将能量输送过程中的网络损耗作为目标函数,进行容量优化和安装方案的选择[6]。近年来,Tabu 算法[7]、遗传算法[8]等智能算法也被应用到储能装置的安装选址问题中,为大规模复杂电力系统的储能优化布局开辟了新的思路。
本文首先建立了CBEST的数学模型,其静态控制采用可独立输出有功、无功功率的发电机模型;暂态计算采用简单的一阶惯性环节来模拟电池的充放电过程[9-11]。通过求解不同运行工况下主导极点对应的特征向量模值,并依据模值的大小对CBEST接入点的优先次序进行排序,以指导CBEST接入点的选择。在PSS/E中利用自定义功能建立了有功功率控制系统数学模型,采用以发电机转子角速度偏差作为输入信号的比例-积分-微分(PID)控制[12-15];最后在IEEE 9节点系统中通过在不同地点设置不同类型的故障,分析各工况下CBEST的最佳接入位置。
1 CBEST的数学模型
本文在PSS/E仿真中采用的CBEST模型是EPRI推荐使用的RP2123-27。CBEST是将电池组、功率转换系统组合而成的模块化的通用电池模型,能够模拟电池的充放电特性,并经过电压源换流器接入电力系统,通过调整电池端电压实现与电网之间的功率交换。储能装置控制器能够独立控制换流器的直流电压和交流合成电压,进而控制CBEST的有功和无功功率。CBEST模型不仅对转换器的交流电流值进行限幅,而且对充放电功率进行限制,以保证电池储能装置工作在安全的环境下。
PSS/E的潮流计算中,CBEST等效为容量足够大、能够满足系统功率需求的发电机,而且为了削弱短路电流的冲击作用,一般设其阻抗为较大的数值。CBEST的数学模型主要包括有功输出、无功输出及限幅环节,其各部分的数学框图模型分别见图1—3。

图1 CBEST有功输出框图Fig.1 Block diagram of active power output of CBEST
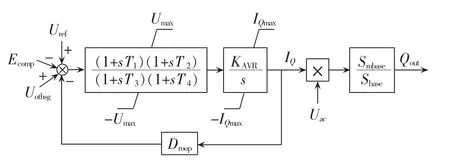
图2 CBEST无功输出框图Fig.2 Block diagram of reactive power output of CBEST

图3 CBEST有功功率控制框图Fig.3 Block diagram of active power control of CBEST
考虑CBEST的容量限制,由图1、图2得到电池储能装置的有功和无功输出表达式为:

而且有:
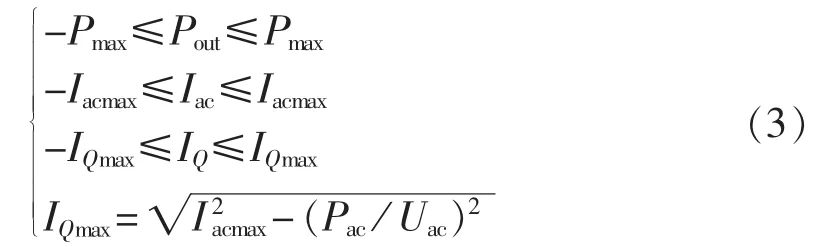
有功功率控制信号的传递函数为:

其中,Paux为储能装置的有功输入信号;Pinit为储能装置的初始输出功率,一般为0;Pout、Qout为储能装置输出有功、无功功率的标幺值;Iacmax为储能装置最大限制电流;Sbase为系统基准容量;Smbase为储能装置基准容量;ΔU 为电压偏差,ΔU=Uref-Ecomp+Uothsg,Uref为控制母线的电压参考值,Ecomp为该母线的电压实际值,Uothsg为稳定器的输出,本文未考虑PSS装置对系统的影响,因此 Uothsg=0;T1—T4为时间常数;Droop为AVR的调差系数;KAVR为AVR的增益;Uac为储能变压器低压侧电压;IQ为低压侧电流的无功分量;Pac为储能装置低压侧输出功率;各物理量的上、下限分别以下标max和min表示;Kω为增益系数;TA和TB为时间常数;Δω=ω-ω0为转子角速度偏差信号,ω0为同步角速度。
2 CBEST最佳安装位置选择的特征向量法
由于系统功率振荡主要受发电机的机械摇摆影响,因此,本文中发电机采用线性化的二阶模型。对于含n台发电机的电力系统,在第i号发电机的母线加装CBEST后,系统的传递函数框图模型如图4所示。图中Mi为第i号发电机的惯性系数,Gii为CBEST的自阻尼力矩系数[3,16],Gij为 CBEST 对第 j号发电机的互阻尼力矩系数,K1、K2为系统参数相关的矩阵。
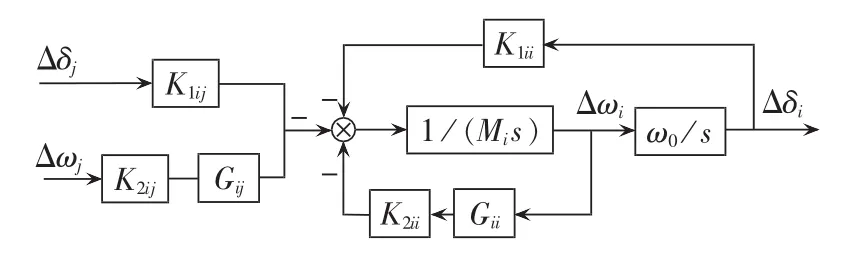
图4 多机电力系统二阶简化模型Fig.4 Simplified second-order model of multi-machine power system
对于第i号发电机有:
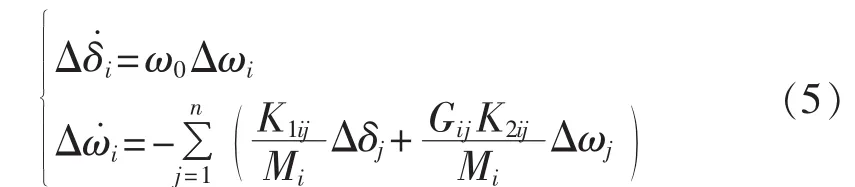
根据式(5)可写出系统的状态方程:

其中,Δδ=[Δδ1,…,Δδn]T为发电机的功角差;Δω =[Δω1,…,Δωn]T为转子角速度偏差;ω0为同步角速度;M=diag(Mi),G=diag(Gij),K1=[K1ij],K2= [K2ij](i,j=1,2,…,n)。 由文献[17]可知:

其中,Pei为第 i号发电机的电磁功率;E′qj和 δj分别为第i号发电机的暂态电势和转子角偏差,均取稳态运行点的数值。
对式(6)中的状态矩阵,设其特征值为 Li(i=1,2,…,2n),相应的特征向量为 ui= [ui1,ui2,…,ui2n]T。记 ui=[uiaT,uibT]T,若不加装 CBEST,则阻尼力矩系数Gii=Gij=0,于是式(6)的特征值可计算为:

其中,I为单位矩阵。
展开上半部分为:

下半部分为:

两式联立,可得:

可见,Li2为矩阵 -ω0M-1K1的特征值,对应的特征向量为uia。通常,将特征向量进行规格化处理,即将uia中最大者取为1.0,并将该值对应的角度取为0°。
特征向量不仅可以衡量某个模式在不同机组上表现的程度,而且可以表示不同机组功角之间的相位差。若特征向量ui中第k个分量uik的模值最大,则认为系统中第k号发电机为功率振荡的主要振源,选第k号发电机为CBEST的最佳安装位置。
3 PSS/E自定义方法
3.1 PSS/E自定义功能介绍
PSS/E用户自定义模型中,根据动态仿真控制标识符调用元件模型子程序CONEC和CONET。通常采用7种标识符实现模型调用,这7种标识符分别是 MODE、KPAUSE、MSTATE、MIDTRM、ITER、IFLAG和IBDOCU。在自定义模型子程序中,通过标识量MODE将子程序分为8个部分,文献[18-19]详细描述了MODE取值1~8的功能,限于篇幅,不再赘述。
PSS/E中元件模型的子程序代码通常使用FORTRAN或FLECS语言编写,然后再编译/连接生成动态链接库文件dsusr.dll以供调用。
书写PSS/E用户自定义模型的步骤如下[19]:
a.建立模型的微分方程及传递函数框图;
b.确定与模型相关的状态变量,并编写求取其时间导数的程序;
c.确定模型的输入、输出量;
d.按需分配整数(ICON)、常量(CON)、状态变量(STATE)、代数变量(VAR)数组的地址;
e.用FORTRAN或FLECS语言编写模型的子程序。
3.2 控制系统实现
为了验证基于特征向量法应用于储能装置选址的正确性,对储能装置接入后的电网进行机电暂态仿真。机电暂态过程的时间尺度为秒数量级,在该时间范围内反映电池特性的指标基本保持不变,可以认为电池在机电暂态过程中的充放电特性和参数是线性和时不变的[10]。因此,可借助线性系统的PID控制进行电池储能控制器设计。本文中CBEST的有功功率控制的框图模型如图3所示。由于在PSS/E的通用模型库中没有现成的控制系统模型,因此CBEST控制器的模型采用PSS/E用户自定义功能实现。
CBEST控制器自定义模型在动态输入文件(*.dyr)中的数据格式如下:

其中,BUSID为模型所连接的母线编号;IM为发电机ID;model name为自定义模型名称;IC为CONEC调用码;IT为 CONET调用码;NI为自定义模型中ICONs的数目;NC为自定义模型中CONs的数目;NS为自定义模型中STATEs的数目;NV为自定义模型中 VARs的数目;datalist为 ICONs、CONs的参数列表。
4 算例仿真
本文采用如图5所示的IEEE 9节点环形系统对特征向量指标进行验证。该系统有3台发电机和3个负荷,发电机G1为平衡节点,其余为PV节点。发电机采用6阶模型,负荷为恒功率模型,系统额定容量为100 MV·A。
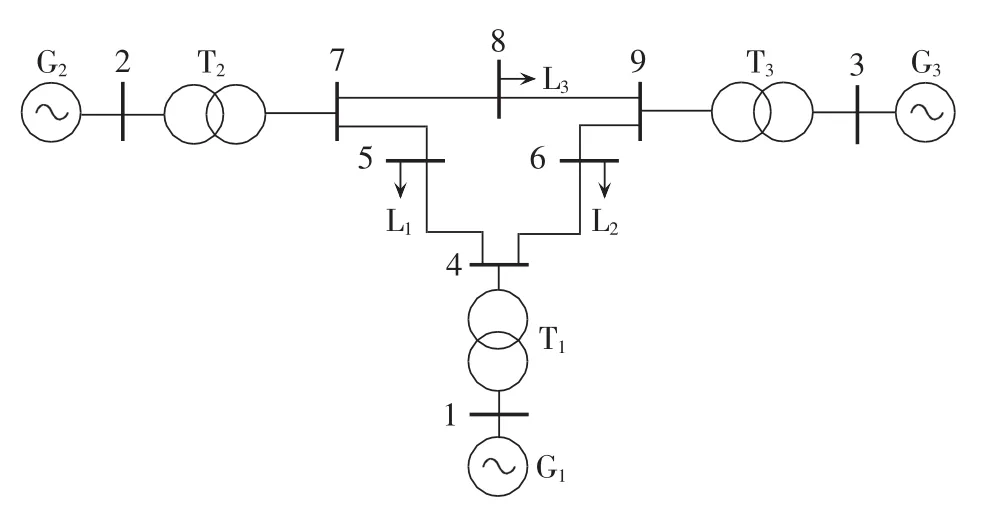
图5 IEEE 9节点系统示意图Fig.5 Schematic diagram of IEEE 9-bus power system
根据式(8)—(11),计算出 IEEE 9 节点系统的特征向量如表1所示,表中uij为特征向量ui的第j个分量。由表1可以得到该系统的主导极点为-0.03078±j0.82027,由于该模式下发电机G1对应的特征向量幅值最大,即发电机G1为功率振荡的主要振源,则选母线1为CBEST的最佳安装位置。在该模式下储能装置最优安装位置排序依次为母线1、母线 2、母线 3。
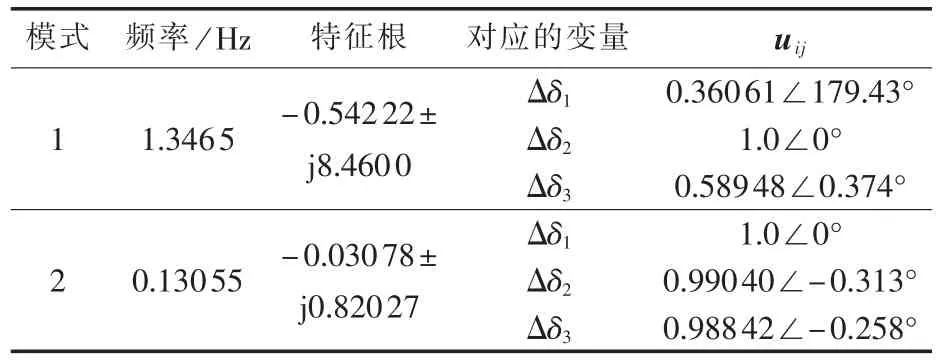
表1 IEEE 9节点系统特征向量计算结果Table 1 Results of eigenvector calculation for IEEE 9-bus system
在时域仿真中通过设置不同类型故障验证特征向量指标的有效性。图6为三相接地短路故障分别发生于母线 1、母线 2、母线 3、母线 5、母线 6,储能接至不同发电机端时,发电机G1输出有功功率(标幺值)变化情况,其他2台发电机暂态过程与G1的仿真结果一致,限于篇幅其仿真曲线在本文中不再给出。为了进一步验证本文方法的有效性,在系统的3个负荷上分别设置±50%的负荷扰动,即在t=1s时,负荷先增大到原来的150%,然后在t=1.01 s时减小到原来的50%,最后在t=1.02 s恢复到原来的大小。当CBEST接至不同位置时,发电机G1的有功功率输出波动情况如图7所示。
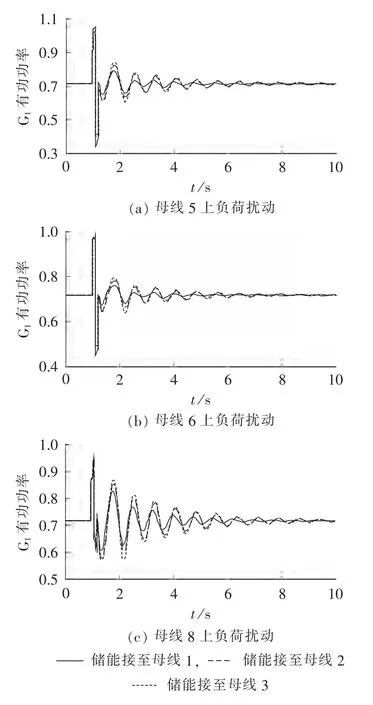
图7 负荷扰动时G1有功功率变化Fig.7 Active power variation of G1with load disturbance
从图6可以看出,无论三相短路故障发生在系统的什么位置,储能装置接在母线1上时对系统的功率振荡抑制效果最好,接在母线2上次之,接在母线3上最差。但接至母线2与母线3上的作用效果差别不大。仿真结果表明储能系统接至母线1时,系统的暂态过渡过程最短。
由图6和图7的仿真结果可以看出,在不同故障位置和故障类型下,储能最佳接入位置的选取具有一致性,即母线1为CBEST最佳装设位置,这与特征向量指标的分析结果相一致,说明IEEE 9节点系统在上述2种工况下采用特征向量指标衡量储能装置最佳装设地点具有较高的准确性。
5 结论
本文建立了CBEST的数学模型,在PSS/E中自定义了储能控制器的数学模型,采用以转子角速度偏差为输入信号的PID控制,得出结论如下:
a.基于特征向量法的基本原理,研究了其用于储能选址的可行性,通过PSS/E小信号分析法对IEEE 9节点系统进行特征值分析,计算了特征根对应的特征向量模值;
b.采用时域仿真分析了在不同运行工况下储能最佳装设位置,仿真结果表明采用特征向量指标选出的储能装设位置具有一定的准确性。
本文采用的方法和结论对于大规模电力系统中储能的优化布局具有一定的参考价值。
