基于距离保护契合因子的区域后备保护方法
2015-09-19郭雅蓉王增平
马 静,郭雅蓉,王增平
(华北电力大学 新能源电力系统国家重点实验室,北京 102206)
0 引言
随着互联大电网的发展,电网结构日趋复杂,传统的仅基于本地信息的后备保护配置与整定愈发困难;同时,系统方式复杂多变,后备保护极有可能出现配合不当或灵敏度不足的情况,因此考虑电网多源信息的广域后备保护研究势在必行[1-2]。
目前,基于广域信息改善和提高继电保护性能的研究大致分为 3 类[3]。
a.基于电气量信息实现广域后备保护功能,如基于电流信息的序电流相位比较和幅值比较的广域后备保护算法[4]、基于电压信息的故障电压比较的广域后备保护算法[5]、基于电压电流综合信息的复合方向元件算法[6-9]和综合阻抗比较算法[10]。
b.基于保护动作信息和断路器开合状态信息实现广域后备保护功能,如基于遗传算法的广域后备保护算法等[11-15],以及考虑算法容错性的广域后备保护算法等[16-19]。
c.综合利用电气量信息和保护动作信息实现广域后备保护功能,如基于保护元件与同步相量测量单元(PMU)数据多源的广域后备保护算法等[20]。
上述算法能够在不改变传统后备保护构成的基础上,通过采集广域信息构建后备保护算法。但现阶段PMU数据受到信息延时的影响,同步性不能得到保障,因此在形成广域后备保护方案时,应尽可能不依赖数据的同步性。另一方面,考虑到基于不同保护原理的保护动作信息和保护动作灵敏度均不同,为了区分不同的保护信息,在权值设置方面应尽可能克服依靠主观经验性知识带来的不确定性问题。此外,尽管现有的通信技术已经趋于完善,但通信系统仍面临着一定风险,信息缺失和错误依旧是广域后备保护系统无法忽视的问题,因此保护方案还必须具备较高的容错性。
本文提出了一种基于距离保护契合因子的区域后备保护方法。首先,将距离保护动作情况对故障识别的贡献程度定义为距离保护贡献度,并将其作为权重构建保护契合度函数和保护契合度期望函数;然后,利用保护契合度函数与保护契合度期望函数之比得到距离保护契合因子,从而识别故障线路。该方法不受信息非同步的影响,在距离保护动作信息的高位数缺失或错误的情况下,仍能准确判断故障线路,同时克服了传统权重设置依靠先前经验带来的不确定性问题,计算量小。最后,IEEE 10机39节点系统的仿真结果与贵州都匀实际系统的实时仿真系统 RTDS(Real Time Digital Simulator)仿真数据均验证了该方法的正确性和有效性。
1 距离保护贡献度
距离保护的整定原则反映了距离保护动作与其正方向发生故障的位置之间的关系。如图1所示,距离保护元件1的Ⅰ段动作,故障仅可能发生在线路L1上;距离保护Ⅱ段动作,故障可能发生在线路L1上或者线路L2的出口处,即图1中点m左侧部分;距离保护Ⅲ段动作,故障可能发生在线路L1、L2上,或者线路L3的出口处,即图1点p左侧部分。

图1 区域电网结构图Fig.1 Structure of regional power network
将距离保护动作情况与故障位置的关系量化。定义距离保护贡献度ωij为距离保护元件j动作时,故障发生在线路Li上的概率。该值反映了距离保护元件j的动作,对判断线路Li是否为故障线路的贡献程度。下面根据距离保护元件的Ⅰ段、Ⅱ段和Ⅲ段与故障线路之间的位置关系,分别推导距离保护Ⅰ段、Ⅱ段和Ⅲ段的贡献度ωⅠij、ωijⅡ、ωijⅢ。
1.1 距离保护I段贡献度
距离保护Ⅰ段只反映本线路故障,当距离保护元件j在故障线路Li上时,贡献度为1;当距离保护元件j不在故障线路Li上时,贡献度为0。由此可得距离保护Ⅰ段贡献度ωⅠij如式(1)所示。

1.2 距离保护Ⅱ段贡献度
线路上任一点故障的概率受到各种因素的影响,如线路所处的地理位置、环境、投运时间等,因此较难确定线路上任一点故障的概率。假设故障随机发生在线路任一点上,用均匀分布来模拟线路上任一点故障的概率。如当保护元件动作,表示保护范围内出现故障,将保护范围覆盖各条线路的部分的阻抗定义为距离保护元件在各线路上的有效距离等值阻抗,保护范围内任一点发生故障的概率用[1,Z]区间的均匀分布模拟,其中Z为保护元件总的有效距离等值阻抗[21]。
距离保护的保护范围是指发生金属性故障时保护的动作范围,该动作范围由整定阻抗决定[22]。如图1所示,元件1的距离保护Ⅱ段的保护范围为点m左侧的范围,即线路qm。该保护元件动作,认为故障发生在线路qm上,且线路qm上任一点发生故障的概率相同,故障发生在线路qr上的概率为lqr/lqm,发生在线路 rm 上的概率为 lrm/lqm,lqr、lrm、lqm分别为线路qr、rm、qm的长度。由于线路的距离与阻抗成正比,可得:,Zqr、Zrm、Zqm分别为线路Lqr、Lrm和Lqm的线路阻抗。距离Ⅱ段元件在各线路上的有效距离等值阻抗计算式如式(2)所示。其中,ZⅡset-j为距离保护元件j的Ⅱ段整定值;线路Li1为线路Li的上级线路,ZLi1为线路Li1的阻抗;KfLi-Li1为线路Li与线路Li1间的分支系数。

式(2)中,当距离保护元件j在线路Li上时,有效距离的等值阻抗为Li的线路阻抗ZLi;线路Li1为线路Li的上级线路,当距离保护元件j在线路Li1上时,在线路Li上产生的有效距离等值阻抗为通过分支系数折算到Li上的阻抗值。
以图1为例,保护元件1的距离Ⅱ段保护范围在L1、L2上产生的有效距离的等值阻抗分别为:

当距离保护元件1的Ⅱ段动作时,故障可能发生在L1、L2上的概率分别为保护范围在各线路上的有效距离占保护范围的总有效距离的比。由式(3)进一步得到距离保护Ⅱ段贡献度ωⅡij如式(4)所示。

其中,N为线路总数。
1.3 距离保护Ⅲ段贡献度
距离保护Ⅲ段可以反映本线路及相邻线路的故障,整定值按照对所有相邻线路都具有灵敏度整定,其保护范围通常可以延伸到相邻二级线路。
按照上述对有效距离等值阻抗的定义,距离保护Ⅲ段的保护范围在线路Li上产生的有效距离等值阻抗为:
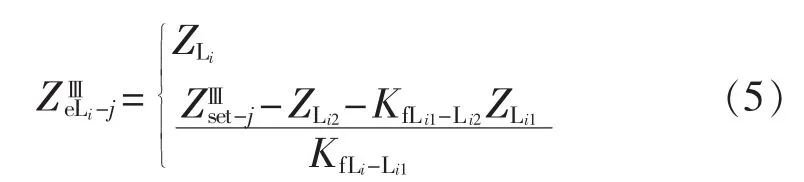
其中,线路Li1为线路Li的上级线路;线路Li2为线路Li1的上级线路为线路 Li2的阻抗为距离保护元件j的Ⅲ段整定值为线路Li和线路Li1间的分支系数;为线路Li1和线路Li2间的分支系数。当距离保护元件j在线路Li或线路Li1上时,有效距离等值阻抗为线路阻抗ZLi;当距离保护元件j在线路Li2上时,其在线路Li上产生的有效距离的等值阻抗为通过分支系数折算到Li上的阻抗值。
以图1为例,距离保护元件1的Ⅲ段保护范围在线路L1、L2上产生的有效距离等值阻抗分别为ZL1、ZL2,在L3上产生的有效距离等值阻抗为:
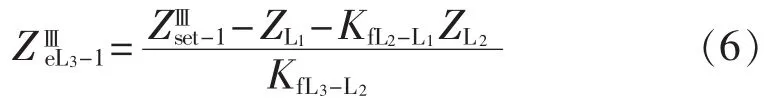
当距离保护元件1的Ⅲ段动作时,故障可能发生在L1、L2、L3上的概率分别为保护范围在各线路上有效距离占保护范围总有效距离的比。由式(6)进一步得到距离保护Ⅲ段贡献度ωⅢij为:

2 基于距离保护契合因子的故障识别方法
2.1 构建保护契合度函数
距离保护贡献度ωⅠij、ωⅡij、ωⅢij分别为距离保护元件j的Ⅰ段、Ⅱ段、Ⅲ段动作,故障发生在线路Li上的概率。将距离保护贡献度作为权重对保护动作信息进行融合,得到线路Li的保护契合度函数:
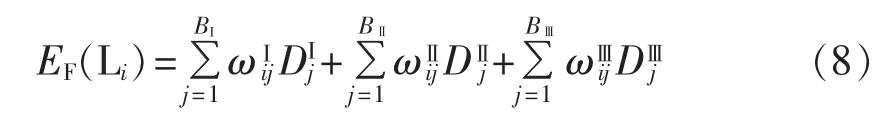
其中,DIj、DⅡj、DⅢj分别为故障发生后距离保护元件 j的Ⅰ段、Ⅱ段、Ⅲ 段的实际动作情况;BⅠ、BⅡ、BⅢ分别为距离保护Ⅰ段、Ⅱ段、Ⅲ段保护元件的数目。保护契合度函数EF(Li)为故障发生后,将各距离保护元件实际动作情况代入计算的结果。
2.2 构建保护契合度期望函数
保护契合度期望函数为假设故障发生在线路Li上,将保护元件动作情况期望值进行信息融合的计算结果。在线路不同位置发生故障,保护元件动作情况不同,因此在确定保护元件动作情况的期望值时需要考虑在线路不同位置发生故障的情况。
以图1中的系统为例。距离保护元件5和6的Ⅰ段的保护范围分别为图2中的2个椭圆部分,2个椭圆将线路L3分为A、B、C这3段,在线路L3不同位置发生故障时,各元件的距离保护I段的动作情况期望值如表1所示(0表示未动作,1表示动作;后同)。

图2 距离保护I段动作情况示例系统Fig.2 Example system for zone-I action of distance protection
故障点在 A、B、C 这 3 段上的概率分别为 λⅠA、λⅠB、λⅠC,计算式如下:
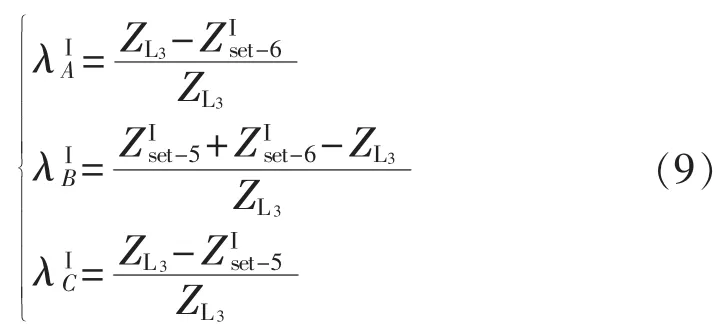
同理,距离保护元件3和8的Ⅱ段的保护范围,也可以将线路L3分为A、B、C这3段,见图3。在线路L3不同位置发生故障距离保护Ⅱ段的动作情况见表2。

表1 线路L3故障时,距离保护I段动作情况Table 1 Action status of distance protection zone-I when fault occurs on L3

图3 距离保护Ⅱ段动作情况期望值计算示例系统Fig.3 Example system for zone-Ⅱaction of distance protection

表2 线路L3故障时,距离保护Ⅱ段动作情况Table 2 Action status of distance protection zone-Ⅱwhen fault occurs on L3
距离保护元件3和8的Ⅱ段的保护范围在线路L3上分别产生的有效距离等值阻抗,可以反映图3中A段和C段的长度,故障点在A、B、C这3段上的概率分别为 λⅡA、λⅡB、λⅡC,计算式如下:

同理,距离保护元件1和10的Ⅲ段的保护范围,也可以将线路L3分为A、B、C这3段,如图4所示。在线路L3不同位置发生故障时,各元件的距离保护Ⅲ段的动作情况如表3所示。
距离保护元件1和10的Ⅲ段保护范围在线路L3上分别产生的有效距离等值阻抗,可以反映图4中A段和C段的长度,则故障点在A、B、C这3段上的概率 λⅢA、λⅢB、λⅢC分别为:
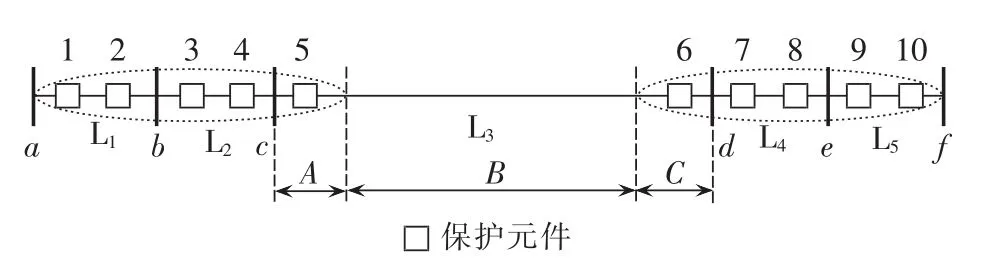
图4 距离保护Ⅲ段动作情况示例系统Fig.4 Example system for zone-Ⅲaction ofdistance protection

表3 线路L3故障时,距离保护Ⅲ段动作情况Table 3 Action status of distance protection zone-Ⅲ when fault occurs on L3

将式(9)—(11)的计算结果作为故障点在线路不同位置时,保护动作情况期望值的权重,得到线路故障时保护动作情况的期望值,则保护契合度期望函数的计算式如式(12)所示。

2.3 基于距离保护契合因子识别故障线路
定义线路Li的保护契合度函数值与保护契合度期望函数值之比为该线路的距离保护契合因子。其计算式如下:

在计算距离保护契合度期望函数值时,考虑到在线路不同位置发生故障的情况,得到的距离保护契合度期望函数值是距离保护契合度函数值的加权平均值,而不是线路某个具体位置发生故障的契合度函数值。因此距离保护契合因子并没有具体的理论值。但是距离保护契合因子的计算是对距离保护契合度函数值进行归一化处理,因此故障线路的距离保护契合因子应为一个接近1的正数。同时,Pe(Li)越大表示保护契合度函数的值越接近保护契合度期望函数的值,则线路Li是故障线路的概率越大,则保护判据为:

区域后备保护算法的具体实现过程如图5所示。
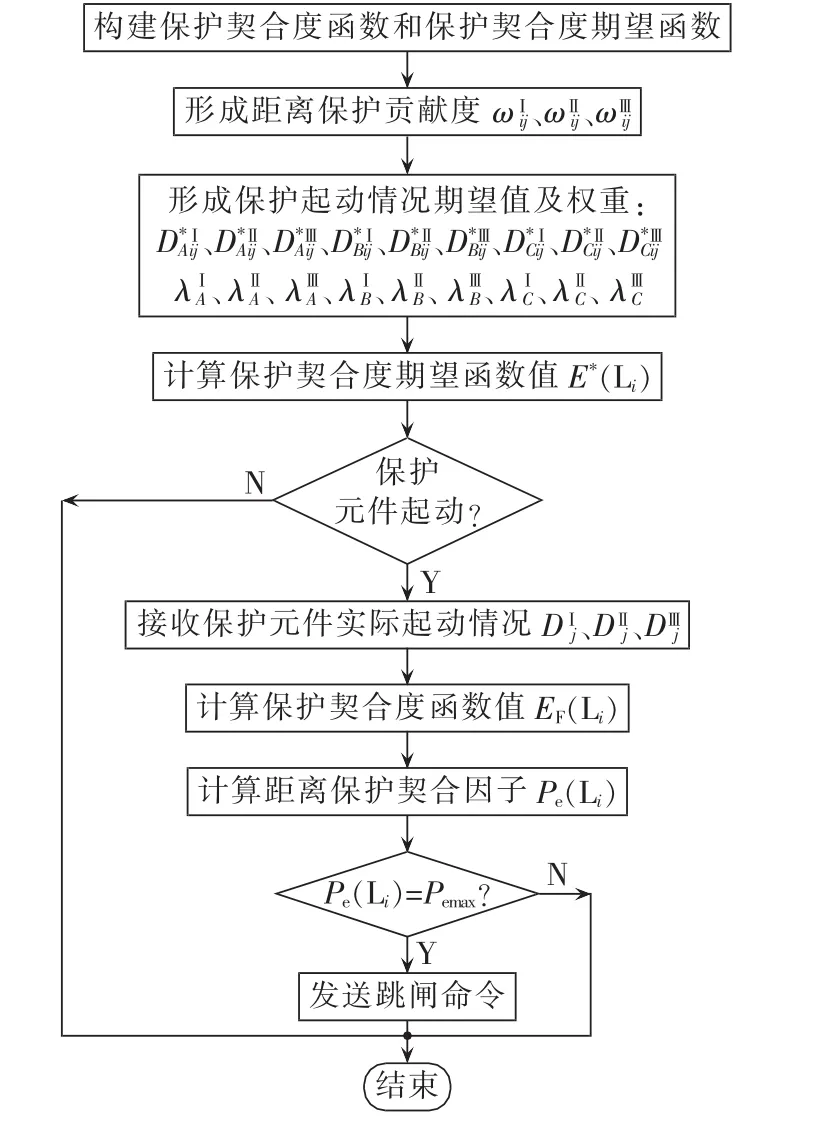
图5 本文所提故障线路识别流程Fig.5 Flowchart of proposed faulty line identification
3 算例验证
3.1 IEEE 10机39节点的系统仿真验证
为验证本文算法的正确性,利用电磁暂态仿真软件PSCAD搭建的IEEE 10机39节点的电力系统模型进行仿真验证,仿真系统图及其各支路和母线编号如图6所示。广域后备保护的构成模式为区域集中式,选取图6中虚线内所示的保护区域为仿真对象(对区域的选择没有特定的要求,所选区域不同并不影响算法的运算结果)。
在线路L8靠近母线4处发生故障。形成各距离保护元件针对每条线路的距离保护贡献度ωⅠij、ωⅡij、ωⅢij,其中对线路L8各距离保护元件的贡献度如表4所示。在实际保护装置中,相间距离保护整定值与接地距离保护整定值不同,可以分别根据整定值计算距离保护贡献度,若相间距离保护动作,则采用相间距离保护整定值计算的贡献度作为权重,若接地距离保护动作,则采用接地距离保护整定值计算的贡献度作为权重。算法不受故障类型不同的影响。

图6 IEEE 10机39节点系统Fig.6 IEEE 10-generator 39-bus system
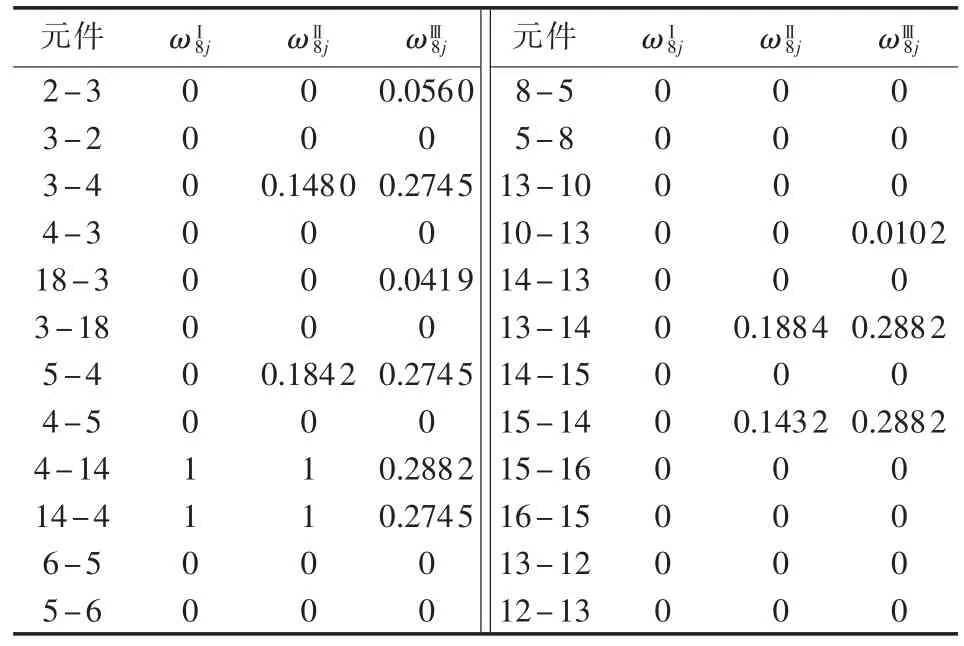
表4 距离保护元件对判断L8为故障线路的贡献度Table 4 Contribution degree to faulty L8identification by different protective elements for three zones
将距离保护贡献度作为权重,结合保护动作情况的期望值及其权重,计算保护契合度期望函数值,如表5所示。
距离保护贡献度、距离保护契合度期望函数值均可以在系统正常运行的情况时,根据保护整定值计算得到,并存储于区域主机中。故障发生后,根据保护的动作情况,只需将保护动作的距离保护元件的信息上传至区域主机,用于计算距离保护契合度函数值,并不需要再搜集整个区域的信息。区域主机接收到各保护元件实际动作情况如表6所示,仅需对15位(即动作情况为1的位数)保护动作信息进行上传,不需要对区域其他信息进行搜集。因此保护的快速性和可靠性能够得到保障。

表5 各线路保护契合度期望函数值Table 5 Value of expected protection fitness function for different lines
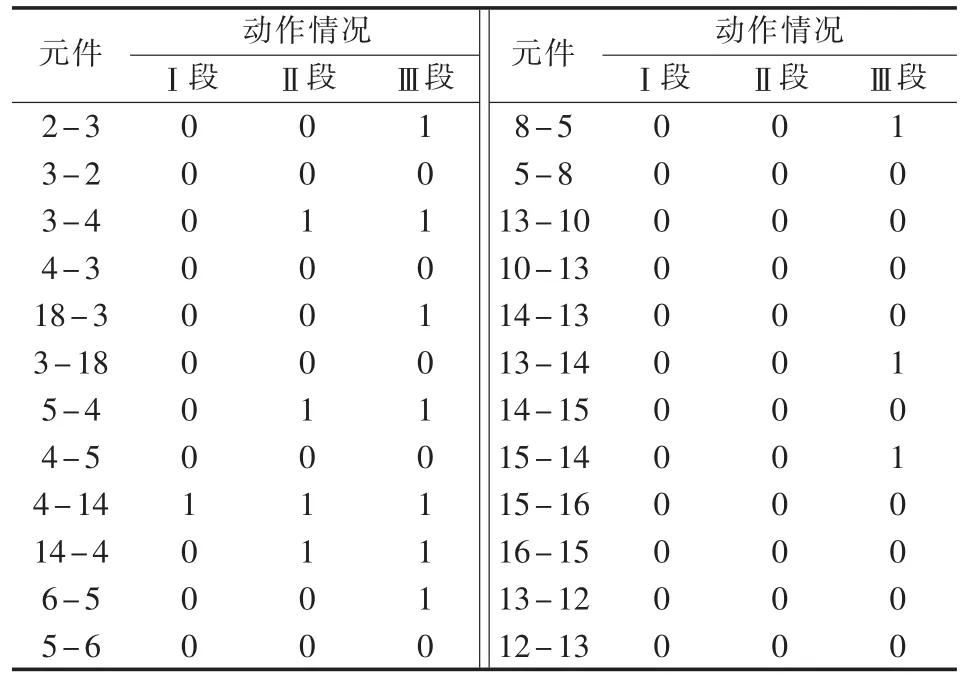
表6 线路L8故障时,各距离保护元件的动作情况Table 6 Action status of different protective elements when L8is faulty
将距离保护贡献度作为权重,由保护实际动作情况计算保护契合度函数值,如表7所示。计算保护契合度函数值与保护契合度期望函数值之比,得到距离保护契合因子,如表8所示。
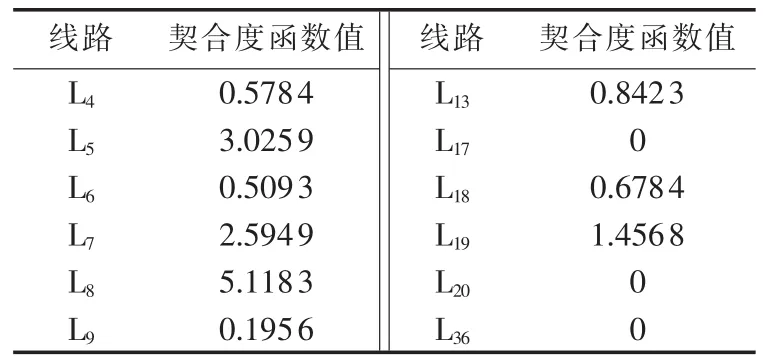
表7 各线路保护契合度函数值Table 7 Value of protection fitness function for different lines

表8 各线路距离保护契合因子Table 8 Distance protection fitting factor of different lines
考察系统的容错性,针对距离保护Ⅰ段,或纵联保护拒动或误动的情况考虑4种特殊情况,以验证本方法的正确性和有效性。
情况1:若线路L8两端的距离保护Ⅰ段均不动作,即表6中的元件4-14的I段动作值为0(此时距离保护I段不能正确判断线路L8故障)。
情况2:若线路L8两端的距离保护I段均不动作,且一端距离保护Ⅱ段拒动,即表6中的元件4-14的I段动作值为0,元件14-4的Ⅱ段动作值为0(此时纵联距离保护拒动)。
情况3:若线路L7一端的距离保护I段误动,即表6中的元件5-4的Ⅰ段动作值为1(此时距离保护I段误判线路L7故障)。
情况4:若线路L7两端的距离保护Ⅱ段均动作,即表6中的元件4-5的Ⅱ段动作值为1(此时纵联距离保护误动)。上述4种情况的距离保护契合因子如表9所示。

表9 4种情况下,各线路距离保护契合因子Table 9 Distance protection fitting factor of different lines for four conditions
由表9中数据可知,线路L8的距离保护契合因子在4种情况下均为区域最大值,满足判据式(14),由此判断线路L8为故障线路。因此,在距离保护I段拒动或误动,以及纵联距离保护拒动或误动的情况下,本方法均能正确判断故障元件。
在对容错性进行分析时,如果逐一对各种情况进行分析,很难枚举到系统可能发生的所有情况。为此,笔者将可能出现问题的所有元件进行N-3处理(超出了系统安全考虑的较严重的N-2情况),以考查本方法的有效性和可行性。如表6所示,线路L8故障后,区域内共有15位保护动作信息。对这15位保护动作信息进行分析,任意N位保护信息错误的仿真结果如表10所示。表中,Pw为错误保护信息数目占保护信息总数目的百分比;X为所有可能情况的统计个数;Y为本方法造成误判的情况数目;本方法正确判断的概率W=(X-Y)/X。
表10中数据显示,15位保护动作信息中任意3位出错,算法均能准确判断故障,且信息容错位数占保护信息总数目的百分比高达20%,表明该算法具有一定的容错性。

表10 所提方法的容错性能Table 10 Fault-tolerant performance of proposed method
本方法在进行故障判断时,只需要搜集故障发生后动作的保护信息,不需要对电气量信息进行搜集。考虑带过渡电阻的短路时,距离保护范围将缩小,动作的保护信息位数也将减少,当保护动作信息减少到0位时(即区域内所有距离保护拒动),本方法不能用于识别故障;当保护动作信息有2位及以上时(如故障线路两端距离保护Ⅲ段动作),本方法可用于识别故障。
以线路L8故障为例进行仿真,得到契合因子如表11所示。由于过渡电阻的影响,各线路的距离保护契合因子均减小,但故障线路的距离保护契合因子仍大于非故障线路,满足判据式(14),可见本方法具备一定的抗过渡电阻的能力。

表11 各线路距离保护契合因子Table 11 Distance protection fitting factor of different lines
3.2 贵州都匀实际系统RTDS仿真验证
以图7所示的贵州都匀110 kV实际系统为例,验证本方法在实际工程中的可靠性。
利用RTDS对图7中线路L6中点发生故障的情况进行分析,各保护元件的动作情况如表12所示,各线路距离保护契合因子如表13所示。

图7 贵州都匀系统Fig.7 Duyun system in Guizhou

表12 线路L6故障时,各距离保护元件的动作情况Table 12 Action status of different protective elements when L6is faulty

表13 各线路距离保护契合因子Table 13 Distance protection fitting factor of different lines
表12中,线路L6故障区域内共有10位保护动作信息,对这10位保护动作信息进行分析,任意N位数信息错误的仿真结果如表14所示。由表14中数据可知,10位保护动作信息中任意5位(N-5)信息错误(超出了系统安全考虑的较严重的N-2情况),本方法均能准确判断故障,且信息容错位数占保护信息总数目的百分比高达50%,表明本方法对实际系统具有一定的指导意义。

表14 所提方法的容错性能Table 14 Fault-tolerant performance of proposed method
4 结论
本文提出了一种基于距离保护契合因子的区域后备保护算法,本方法具有以下特点:
a.引入距离保护贡献度,作为距离保护契合度函数和契合度期望函数中的权重值,该权重值根据距离保护的保护范围定量计算得出,克服了传统权重设置依赖先验经验带来的不确定性问题;
b.本方法具有很高的容错性,保护动作信息任意3位数(容错百分比为20%)、任意5位数(容错百分比为50%)出错,故障判断的准确率仍为100%;
c.故障发生后,本方法仅需要搜集各保护的动作信息,需要上传的信息量少,且对通信系统的同步性没有要求;
d.不需要进行保护定值的计算,只需要对区域内线路的距离保护契合因子进行横向比较,进而定位故障。
