同塔双回线接地距离保护零序电流补偿系数分析及整定方法改进

2015-09-19姜宪国周泽昕杜丁香李仲青

电力自动化设备 2015年8期

姜宪国，刘宇，周泽昕，杜丁香，李仲青

（1.中国电力科学研究院电网安全与节能国家重点实验室，北京 100192；2.国家电力调度通信中心，北京 100031）

0 引言

同塔双回线路[1-2]共用杆塔，能够充分利用有限的输电走廊资源，减少占地面积，并且具有建设速度快、输电能力强等优势，因此在实际工程中得到了广泛的应用。然而受双回线零序互感[3-6]的影响，线路接地距离保护存在误动或拒动的风险，威胁系统安全。

针对零序互感问题，一种解决方法[7-8]是引入邻线的零序电流进行补偿。但由于双回线运行方式多变，常常会使补偿后的实际效果适得其反[9]，难以达到理想的保护性能，且引入邻线信息会增加保护配置复杂度。另一种方法[10-11]是根据系统运行方式实时切换零序补偿系数（K值），使继电器尽可能准确地反应故障阻抗。但该方案涉及定值自动切换，影响保护可靠性，目前现场仍无法接受。实际中，接地距离保护均采用固定K值进行计算，具体分为单K值整定和双K值整定2种策略。

本文首先比较同塔双回线4种典型系统运行方式下零序补偿系数的大小关系，并对现有单/双K值整定方法存在的问题进行了分析，分析结果表明双K值整定的性能优于单K值整定。进一步针对目前双K值整定策略提出改进方法，用于提高保护可靠性。最后通过PSCAD仿真验证所提方法的有效性。

1 同塔双回线零序补偿系数

1.1 双回线零序补偿系数表达式[10]

如图1所示，双回线一回发生接地故障时，考虑另一回对其产生的零序互感，则故障线路保护安装处电压为：

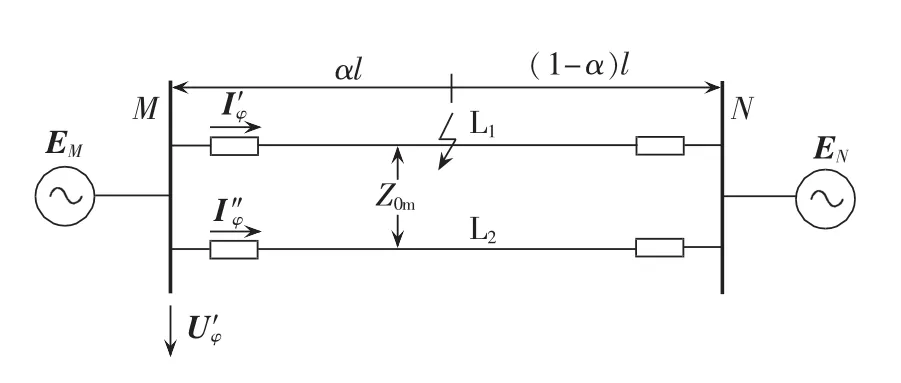
图1 同塔双回线示意图Fig.1 Schematic diagram of dual-loop lines on same tower

其中，I′φ为线路 L1故障相的电流；I′1、I′2、I′0分别为线路L1的正、负、零序电流；I″0为线路L2的零序电流；α为线路故障点与首端距离占线路全长的百分比；Z1、Z2、Z0分别为单回线路的正、负、零序阻抗；Z0m为双回线零序互感阻抗。

从而得到接地阻抗继电器的测量阻抗为：

借鉴单回线零序补偿系数的构成形式，定义双回线零序补偿系数的表达式为：

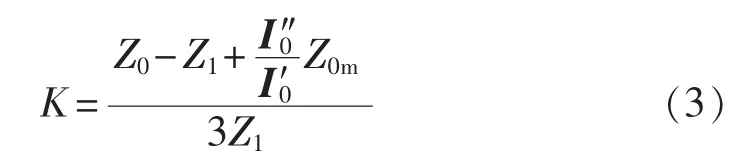
由式（3）可见，双回线零序补偿系数不仅与各回线自身参数有关，还与线间零序互感阻抗以及流过的零序电流有关。

1.2 4种典型运行方式下的零序补偿系数

此处列举双回线可能出现的4种典型的运行方式，分析中近似认为双回线的Z1、Z0和Z0m相位相同，着重比较不同运行方式下K值的大小关系。

a.双回线同时运行。

双回线同时运行且一端母线发生接地故障（见图2）时，此时存在：

可得：

图2 双回线同时运行Fig.2 Both loops are operating

b.一回线停运（两端不接地）。

如图3所示，当一回线停运时，零序互感系数与无互感的单回线路相同，表示为K2：

图3 双回线一回停运Fig.3 One loop is in outage

显然，此时的K2小于双回线同时运行的零序互感系数K1。

c.一回线检修（两端接地）。

当一回线检修而运行线一端母线发生接地故障（见图4）时，检修线路的电压平衡方程为：

从而可得：

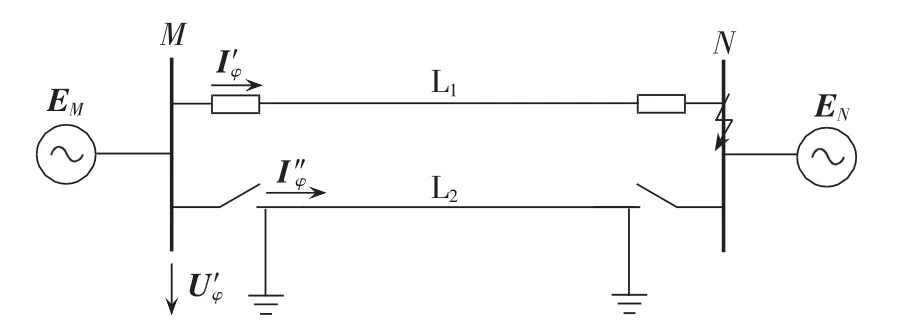
图4 双回线一回检修Fig.4 One loop is in maintenance

可见该系数小于一回线停运时的零序补偿系数K2。

d.一端母线解列运行。

双回线一端母线解列运行且解列端出口发生接地故障的示意图如图5所示。为简化分析，仅考虑线路L2与L1零序电流反向的情况，则线路L1零序补偿系数可表示为：

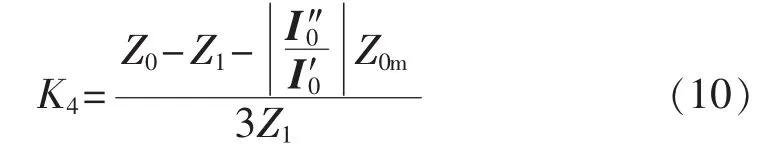
结合式（3）、（8）可得运行线路的零序补偿系数为：

图5 双回线一端解列Fig.5 One terminal of dual-loop lines is disconnected

由式（10）可见，K4的大小受线路L2零序电流与L1零序电流比值的影响，若该比值小于Z0m/Z0，则K4＜K3，反之则 K3＜K4。

综上所述，4种典型的运行方式对应故障线路的4个不同K值，其大小关系如下：

2 距离保护采用单K值存在的问题

由上文可知，同塔双回线路在不同运行方式下具有不同的零序补偿系数。因此，接地距离保护[13-16]除需要整定阻抗Zset外，还需要整定合理的零序补偿系数K。

对于距离Ⅰ段，为保证本线路末端故障不误动，在4种运行方式对应的不同K值之间，应采用最小的K值。对于距离Ⅱ段，由于要求在线路末端故障时具有足够灵敏度，因此在不同的K值之间应该选用最大K值进行计算。

2.1 单K值整定方法

目前部分双回线距离保护中采用了单K值整定方法，即距离Ⅰ、Ⅱ段采用同一个K值。其中典型的整定原则如下。

a.接地距离Ⅰ段的零序补偿系数按双回线一回检修时的K3值进行计算，Ⅰ段的可靠系数KIrel取正常值0.7。

b.接地距离保护Ⅱ段的零序补偿系数同样取K3，而其可靠系数则在原基础（KⅡrel=1.3）上乘以修正系数 KⅡx。

其中，K1为双回线同时运行时的零序补偿系数。

理论上距离Ⅱ段应选取最大值K1进行计算，而在单K值的整定原则中距离保护Ⅰ、Ⅱ段均采用了K3进行计算。为了保证距离Ⅱ段应有的灵敏度，于是对其可靠系数乘以修正系数KⅡx，以弥补单K值造成的影响。

2.2 单K值特性的定性分析

目前整定方法采用的小K值为一回线检修时对应的零序补偿系数K3，而由前文分析可知，K3并非在所有运行方式中均为最小的K值，这一问题将在后文中具体分析，本节分析单K值本身的特性。

单K值的整定方法相当于将原本零序补偿系数的问题转嫁给了整定阻抗，如果转嫁后仍能满足保护性能要求，这样处理亦无不可，但若无法满足，则可能引起保护不正确动作，以下进行具体分析。

当双回线同时运行且一端母线发生接地故障（见图2）时，为便于比较，将修正系数 KⅡx，由整定阻抗中折算到测量阻抗中，则距离Ⅱ段的测量阻抗和整定阻抗分别为：

而此时实际的零序补偿系数为K1，因而有：

结合式（14）和式（15）可知，若欲使距离Ⅱ段的测量阻抗（折算后）等于实际短路阻抗，则需要满足条件：

而式（15）的等式关系受负荷电流和各序电流分配系数的影响，通常无法满足，由此会对保护性能造成影响。

2.3 单K值特性的定量分析

为进一步分析单K值整定的保护性能，以图2为例，考虑较严重情况，假设M端系统正序阻抗ZMS1很大而零序阻抗ZMS0很小，N端系统正序阻抗ZNS1很小而零序阻抗ZNS0很大，且故障前负荷电流为0，这时若 N 端母线发生接地故障，即存在 I′φ=I′0。近似认为Z0=3Z1，针对不同的零序互感阻抗（通常为零序自阻抗的20%～80%），计算线路L1的M端保护接地距离Ⅱ段测量阻抗与整定阻抗的比值，结果如表1所示，表中粗体表示保护会不正确动作，后同。

表1 不同零序互感阻抗下的接地距离保护Ⅱ段测量阻抗Table 1 Measured impedance of grounding distance protection zone-Ⅱfor different zero-sequence mutual inductances

由表1可见，在给定运行方式下，采用单K值整定后距离Ⅱ段灵敏度会随着双回线零序互感阻抗的增加而显著降低。当零序互感阻抗达到一定值时，Ⅱ段保护发生拒动。

单K值另一种整定方法是距离Ⅰ、Ⅱ段均采用K1进行计算，并对距离Ⅰ段整定阻抗乘以修正系数 KIx：

当实际运行方式为一回线检修（见图4）时，为便于比较，将修正系数KIx由整定阻抗中折算到测量阻抗中，则距离Ⅰ段的测量阻抗和整定阻抗分别为：

而此时实际的零序补偿系数为K3，因而有：

仍按前述的运行方式计算距离Ⅰ段测量阻抗与整定阻抗的比值，结果如表2所示。

表2 不同零序互感阻抗下的接地距离保护Ⅰ段测量阻抗Table 2 Measured impedance of grounding distance protection zone-Ⅰfor different zero-sequence mutual inductances

由表2可见，当实际运行方式为一回接地检修，且故障电流中相电流与零序电流不符合3倍关系时，随着双回线零序互感阻抗的增加，距离Ⅰ段的可靠性即降低，当零序互感阻抗达到一定值时，保护即发生误动。

综上所述，单K值整定方法将原本零序补偿系数的问题转嫁给了整定阻抗，而在较严重的系统工况下，这种转嫁存在导致保护拒动和误动的可能性。

3 距离保护双K值整定方法的改进

现行保护装置中还有一种双K值的整定方法。其整定原则为：距离Ⅰ段采用一回线检修接地对应的K3值，可靠系数取0.7；距离Ⅱ段采用双回线同时运行对应的K1值，可靠系数取1.3。该整定方法分别采用不同的K值以兼顾距离Ⅰ、Ⅱ段保护的性能需求，因此较单K值更具有合理性。

3.1 传统双K值整定的问题

距离Ⅰ段要求在各种运行方式下线路末端故障不误动，理论上其K值应整定为所有运行方式中最小的K值。然而现行双K值整定中，距离Ⅰ段采用K3值进行计算，由式（11）可知，当一端母线解列运行时，存在K4＜K3的情况。此时距离Ⅰ段如仍用K3计算测量阻抗，则可能会导致可靠性下降甚至保护误动。

为明确K3与K4差异带来的影响，在图5所示网络中，假设正常时负荷电流为0，考虑较严重情况，设M端系统及N2端系统正序阻抗较大，而N1端系统正序阻抗较小，则在N1端出口发生故障时，线路L1和L2中仅有零序电流流过。同时由于高压线路两端系统通常都有零序回路，M端系统总会存在零序分流，因此设置在[0.1，0.9]之间进行考察。则在不同零序互感阻抗以及不同零序电流比时，距离Ⅰ段测量阻抗计算结果如图6所示。

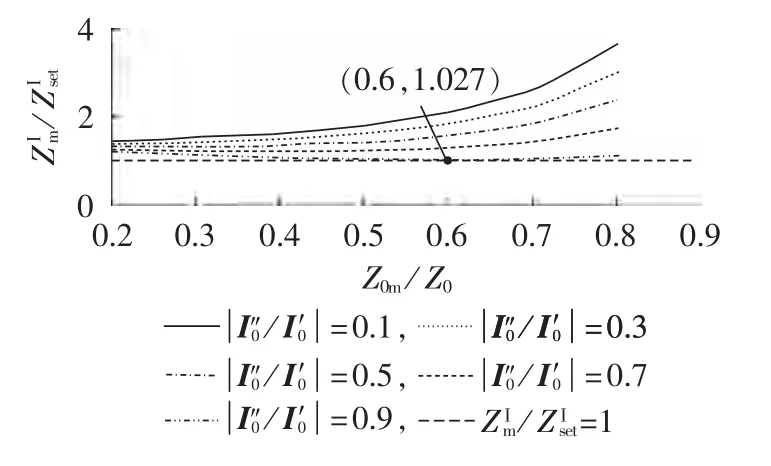
图6 采用传统双K值整定方法时接地距离保护Ⅰ段动作情况Fig.6 Performance of grounding distance protection zone-Ⅰwhen traditional dual-K setting is adopted

由图6可见，随着线路L2零序分流越大，距离Ⅰ段测量阻抗越趋近于整定阻抗。当且时，测量阻抗基本等于整定阻抗，保护很可能会发生误动。

3.2 双K值整定方法的改进

传统双K值的距离Ⅰ段之所以有误动风险，是由于其整定所采用的K值，并非各种系统运行方式下故障线路可能出现的最小K值。从理论上，对于图5所示运行方式，当线路L2零序电流与线路L1幅值完全相同、方向相反时，K4取到最小值为：

由于同塔双回线Z0m总小于Z0，因此K4.min总小于K3，即为各种运行方式下故障线路可能出现的最小零序补偿系数。若仅考虑保护可靠性，可将距离Ⅰ段的零序补偿系数直接整定为K4.min，能够保证Ⅰ段在任何运行方式下均不会误动。

但如前文所述，通常情况下M端系统总会有零序分流，因此K4不可能取到最小值K4.min。且根据保护四性的要求，在距离Ⅰ段可靠性得以保证的前提下，应尽可能提高其灵敏性，零序互感系数若整定得太小，会使Ⅰ段保护范围大幅缩小。

鉴于以上原因，对双K值方法中距离Ⅰ段零序补偿系数的整定作如下改进，即取值K3和K4.min值的加权平均数K5：

显然K5值介于K3和K4.min之间，仍按图6对应的系统运行方式分析由K5值整定的距离Ⅰ段动作情况，结果如图7所示。

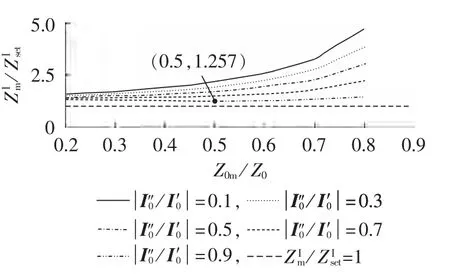
图7 采用改进双K值整定方法时接地距离保护Ⅰ段动作情况Fig.7 Performance of grounding distance protection zone-Ⅰwhen improved dual-K setting is adopted

由图7可见，采用K5值进行计算后，距离Ⅰ段在线路末端故障时可靠性明显提高，各种情况下的最小可靠系数亦达到1.257，有效防止了保护误动的可能性。

综上所述，对同塔双回线双K值方法改进后的接地距离保护整定原则为：

a.距离Ⅰ段零序补偿系数采用K5值进行计算，其可靠系数选为0.7；

b.距离Ⅱ段零序补偿系数采用K1值进行计算，其可靠系数选为1.3。

采用如上方法整定后，既能避免距离Ⅰ段超越误动，又能保证距离Ⅱ段对线路末端故障有足够灵敏度，特性良好。

4 仿真验证

利用PSCAD搭建仿真系统如图1所示，双回线线路参数为：线路长度l=200 km；单回线参数，Z1=0.01+j0.267ω /km，XC1=-j0.233 MΩ·km，Z0=0.18+j1.107ω /km，XC0=-j0.648 MΩ·km；双回线互感参数，Z0m=0.18+j0.704ω /km。 M 端系统参数，E′M=500∠0°kV，ZMS1=70.3∠80°Ω；ZMS0=80.5∠80°Ω；N 端系统参数，E′N=525∠30°kV，ZNS1=15.2∠80°Ω，ZNS0=800∠80°Ω。杆塔结构如图8所示。

图8 双回线杆塔结构Fig.8 Structure of tower of dual-loop lines

仿真故障类型包括：（1）双回线同时运行，N端出口发生单相接地故障（见图2）；（2）线路 L2停运，线路L1N端出口发生接地故障（见图3）；（3）线路L2挂地线检修，线路L1的N端出口发生单线接地故障（见图4）；（4）双回线 N 端解列运行（见图5），M 端系统电动势参数不变，阻抗参数变化为ZMS1=703∠80°Ω，ZMS0=805∠80°Ω，N1端系统参数与原N端参数相同，N2端系统电动势和正序阻抗与原N端参数相同，零序阻抗变为ZN2S0=80∠80°Ω，此时N1端出口发生单相接地故障。在以上故障类型下，计算相量的相角（保护动作判据为°，其中，Zm为阻抗继电器的测量阻抗）。故障发生在0时刻，仿真时长0.5 s，测量数据取自0.5 s时刻。

针对仿真内容对应的4种不同运行方式，得到不同的零序补偿系数，结果如表3所示。