含分布式电源的配电网三相时域仿真

徐青山，刘中泽，陈潇鹏，杨永标，黄 莉

（1.东南大学 电气工程学院，江苏 南京 210096；2.南京南瑞继保电气有限公司，江苏 南京 211102；3.国电南瑞科技股份有限公司，江苏 南京 210003）

0 引言

能源是人类赖以生存的基础，随着旧能源的长期消耗，人类面临着常规能源枯竭、环境问题凸显难题，开发清洁的新能源以节能减排、改善人类生存环境是全人类共同的责任。作为利用可再生能源的主要形式，分布式电源（DG）以投资小、清洁环保、供电可靠和发电方式灵活等优点赢得了快速发展[1-3]。配电网作为最主要的中小容量、分散式分布式电源接入网络，当分布式电源的数量及容量接入提升，可能会对配电网的运行、电能质量、局部电压稳定性等有不利影响[4-5]，其中电压稳定性属于暂态问题。

传统配电网动态元件较少，暂态研究几乎没有，而分布式电源的接入使含分布式电源的配电网、微电网的暂态研究开始得到关注[6-9]。但现有的含分布式电源暂态仿真并未深入涉及网络不对称问题，大多采用MATLAB、PSCAD、DIgSILENT等商业软件进行仿真[10-12]。自行设计仿真算法，可了解仿真中计算过程及可能带入的问题，然后进行分析，得出解决方案。

配电网潮流是配电网暂态问题研究的起点，现阶段配电网潮流计算及含分布式电源的配电网潮流计算的研究已有很多，研究问题有三相不平衡问题处理、潮流算法选择、分布式电源节点的处理等[13-16]，也存在一些问题，如配电网仿真案例节点普遍较少、部分仿真未考虑配电网不对称问题而采用单相或各序潮流计算、分布式电源接入种类及个数较少等。

暂态时域仿真有两大核心内容：一是动态元件的建模问题；二是选取的微分方程积分方法以及各类误差的控制，微分的积分方法相对比较固定，误差控制与模型接口、积分方法有关。现有研究主要有分布式电源的建模、分布式电源以及微网的并网稳定性等，存在的问题有：分布式电源建模研究较多但机网接口处理方法研究较少，建模没有通用的模型[17-18]。暂态仿真方面也主要是针对微电网，如单个分布式电源的PQ或者Vf控制，孤岛时Pf下垂参与负荷分配，分布式电源参与孤岛微电网调压、调频等[19-20]。

本文从最基础的动态元件建模入手，实现了分布式电源共性部分建模，借鉴输电网单相时域仿真方法，分析配电网存在的特殊问题，研究配电网三相时域仿真方法，解决了分布式电源与配电网的模型接口处理问题，并通过实际编写程序，最终实现含分布式电源的配电网全网机电暂态仿真。

1 分布式电源模型

配电网主要的元件有线路、负荷、分布式电源，其中线路模型一般采用准稳态模型，三相形式为：

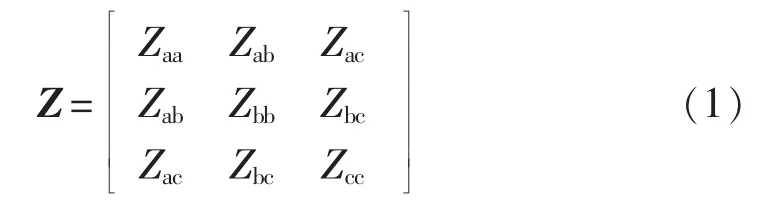
其中，Zaa、Zbb、Zcc为线路自阻抗；Zab、Zac、Zbc为线路互阻抗。

负荷一般看作恒阻抗模型，若考虑静态负荷和动态负荷可以参考输电网处理方法[21]。本部分着重就动态元件分布式电源的模型进行分析。

分布式电源的控制方式通常有3种：微电网并网状态下的PQ控制方式，微电网孤岛状态下的调速差Droop控制以及Vf控制。由于含分布式电源的配电网相当于微电网并网运行状态，所以本文只考虑了分布式电源的PQ控制。

PQ控制要求电网侧电压是对称的，此处先认为网侧电压对称（后文具体解决不对称问题），分布式电源建模还需假设忽略谐波问题，认为逆变器的输出始终是三相对称基波正弦量。

图1给出了典型的分布式电源逆变器并网拓扑，L是滤波电感，R是逆变器装置所有损耗等值电阻，ugabc是逆变器网侧电压，uabc是逆变器输出的交流电压。为简化问题，以恒定直流压源Udc代替各类分布式电源的源侧，随着储能技术和直流微网技术的发展，这样的简化也具有一定的意义。

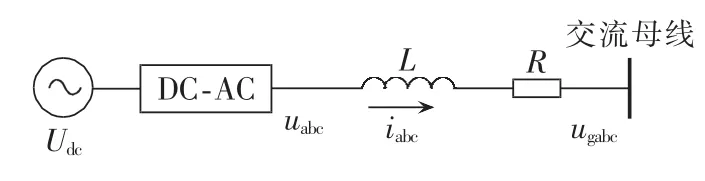
图1 分布式电源并网拓扑Fig.1 Grid-connection topology of DG

1.1 分布式电源电路标幺值模型

按图1，分布式电源电路拓扑图主要由直流电源、逆变器和滤波器构成，其中逆变器模型有2种：开关函数模型和占空比模型[2]。开关函数模型一般用于电磁暂态仿真中并进行精确的瞬时值仿真，同时也需要所有元件都采用电磁模型，本文侧重于进行有效值计算的机电暂态仿真，逆变器采用占空比模型，忽略逆变器的各种开关状态，认为逆变器输出电压是受占空比控制的对称正弦电压。

设系统侧三相对称电压为：

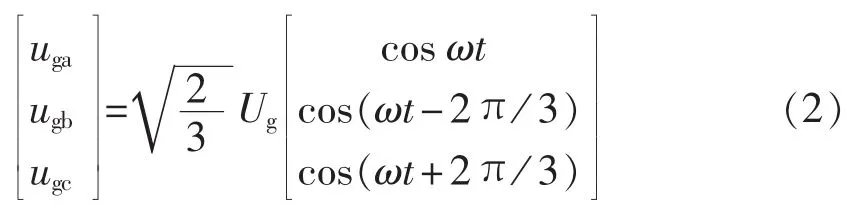
其中，Ug为网侧线电压的有效值。

假设逆变器输出电压相位超前网侧电压δ，则：

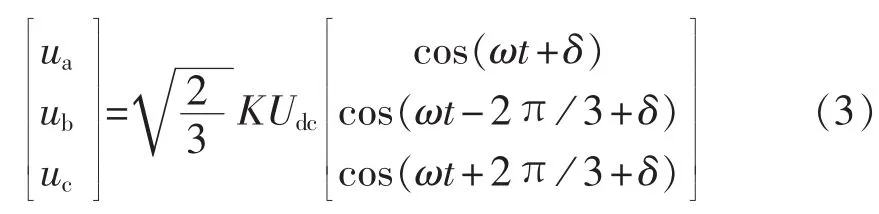
其中，K为逆变器变比，定义为逆变器输出线电压与逆变器直流侧电压的比值。

图1时域电路方程为：

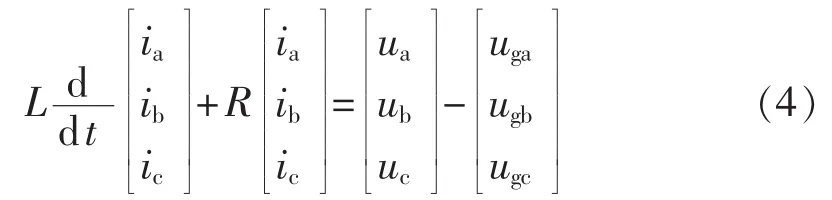
由于逆变器的控制是在dq轴进行解耦的，可采用正交Park变换得到dq轴下电路模型，变换阵相角和网侧电压相位一致，即：

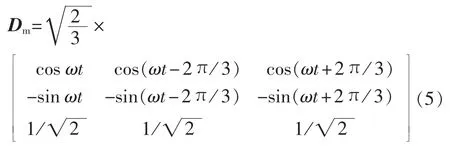
对电压向量正交Park变换有：

将式（3）代入式（4）并用式（5）变换矩阵进行正交Park变换，得到分布式电源电路模型有名值方程：

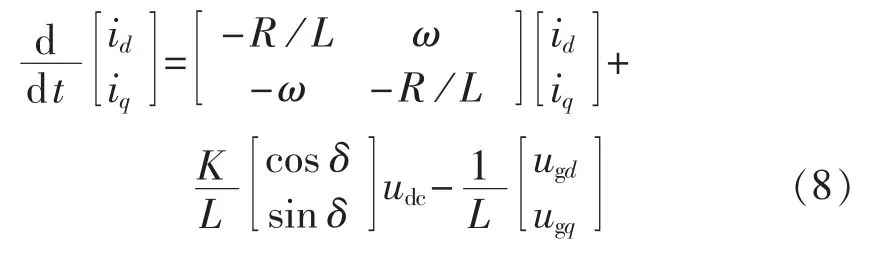
按式（6）有ugq=0，为说明原理及书写对称性，本文所有出现ugq的地方都指ugq=0，但保留变量ugq书写形式。

选择网侧基准值对各动态元件进行标幺化，使得全网动态元件与网络的接口处理变得更加简单。标幺化以后的变量、参数能够摆脱具体物理量的限制，反映出模型的数学本质特征。取网侧线电压、功率基值分别为UB、SB，则，分布式电源侧dq坐标系选，由，得，选时间基值，至此所有量的基准值都已选取完毕。

按上述基准值将式（8）进行标幺化得到分布式电源电路模型的标幺值方程：

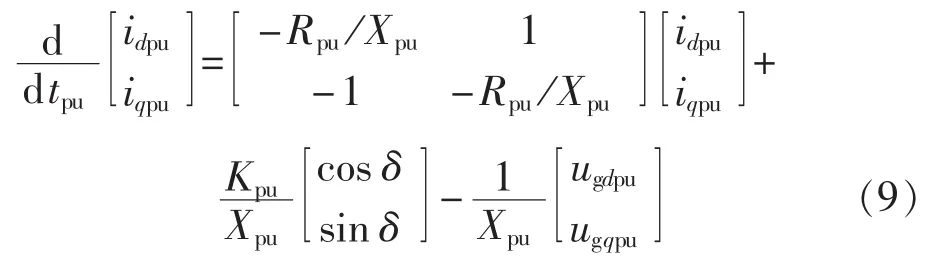
其中，下标pu表示标幺值参数。

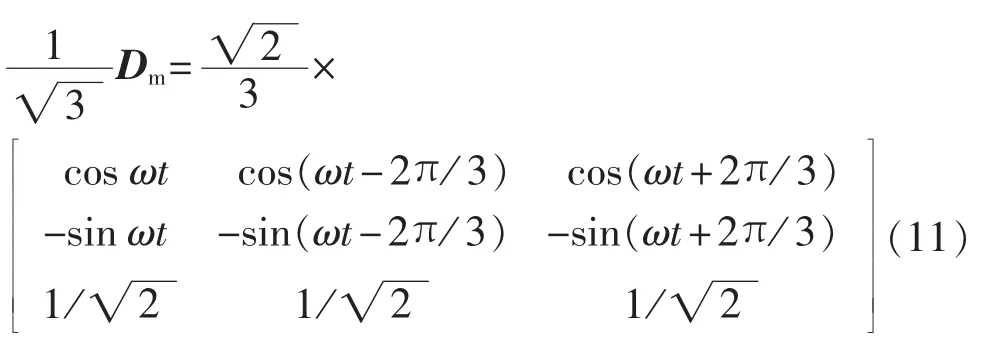
为方便书写，以下略去所有标幺值参数的下标“pu”，无特殊说明所有量都是指标幺值；以下正交Park变换都简称Park或Dm变换。

1.2 分布式电源控制器模型

分布式电源PQ控制策略是指按照给定功率参考进行输出，电网中的负荷波动带来的电压问题、不平衡问题由大电网进行平衡。PQ控制策略采用功率外环以及电流内环组成，控制方式一般可以采用PI环节。

1.2.1 功率外环

dq轴下的分布式电源向电网注入功率为：

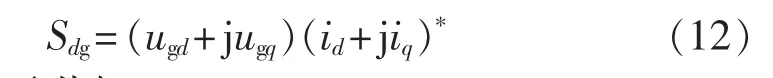
其中，“*”表示共轭。

当变换阵相角采用和网侧电压相位一致时有ugq=0，代入式（12）得：

可以通过控制 id、iq来分别控制分布式电源的有功、无功输出，即功率解耦控制，前提是式（2）、（5）成立。功率环的控制图如图2所示。

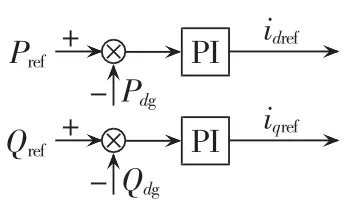
图2 功率外环控制Fig.2 Outer-loop power control

1.2.2 电流内环

功率外环控制得到了id、iq的参考输出值 idref、iqref，为实现精确的电流内环控制，需要考虑实际电路模型。对式（9）进行整理得到：

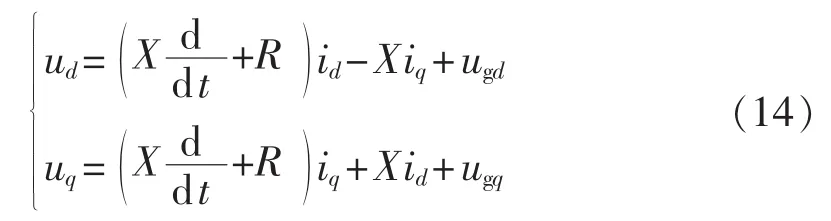
电流内环的控制是为了通过给定电流参考控制电流得到需要的电压PWM波信号，最理想的是能通过 id、iq分别控制 ud、uq。根据式（14）知逆变器输出电压、电流的dq轴量存在耦合，表现在iq影响了ud、id影响了uq，此外还受网侧电压ugd影响，可采用前馈解耦控制策略来实现去耦合，当电流环也采用PI调节器时，按此思想的控制方程为：

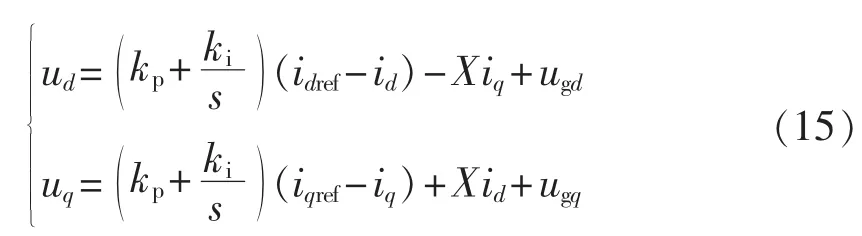
其中，kp为比例调节系数；ki为积分调节系数。

按式（15）绘制出电流内环解耦控制图如图3所示。

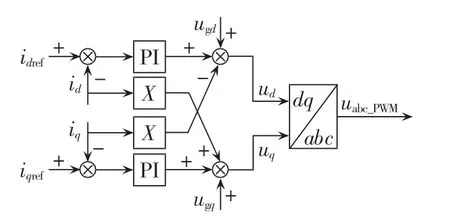
图3 电流内环解耦控制Fig.3 Inner-loop decoupled current control

综上，完整的PQ控制框图如图4所示，需要说明的是：

a.图中所有参数、变量都应当是标幺值；

b.各PI输出值和变比K可以设置一个限幅环节；

c.R+jX是滤波器和损耗环节，其逆变器侧电压由控制器输出给定，模型见式（9）；

d.全图成立的前提是网侧电压ugabc三相对称且变换阵的相位与网侧电压相位一致；

e.式（13）中 Qdg与 iq呈负相关，图中 PI3环节前必须添加负号。

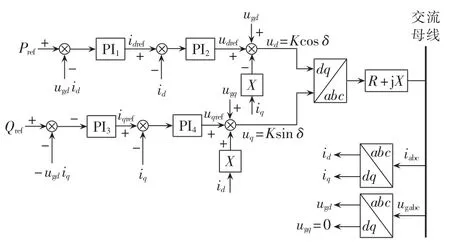
图4 分布式电源PQ控制全图Fig.4 Schematic diagram of PQ control for DG

2 配电网三相时域仿真

时域仿真要将电力系统各元件模型根据元件拓扑关系形成全系统模型，得到联立的微分方程组和代数方程组，其中网络是线性的，微分方程主要存在于动态元件中。通常以稳态潮流解为时域仿真的初值，求扰动下的数值解，观察扰动下系统各状态量或者代数量的变化曲线，以此来判断系统的稳定性。时域仿真作为一种方法，本身不存在单相与三相的差别，只是求解形式不同而已，借鉴于输电网时域仿真过程，图5给出了配电网机电暂态时域仿真的一般过程。

图5 配电网机电暂态仿真一般过程Fig.5 General process of electromechanical transient simulation for distribution network

2.1 分布式电源网侧不对称电压处理方法

无论是分布式电源的逆变器电路模型还是控制器设计都是按照网侧电压三相对称且变换阵的相位与网侧电压相位一致的前提推导的，而实际配电网存在网络不对称和运行不对称现象，必然导致各节点网络电压不对称，为此需要解决对称模型与实际不对称电网电压之间的矛盾。实际配电网各节点网络电压不对称，但正常时电压不对称度较低，按照GB/T15543—2008规定电力系统公共连接点及负荷节点负序电压不平衡度均不超过5%。由逆变器输出得到的分布式电源的注入电流也接近正弦，即电流的不对称度也较低（假设也小于5%）。按照对称分量法（φ=2π/3）：

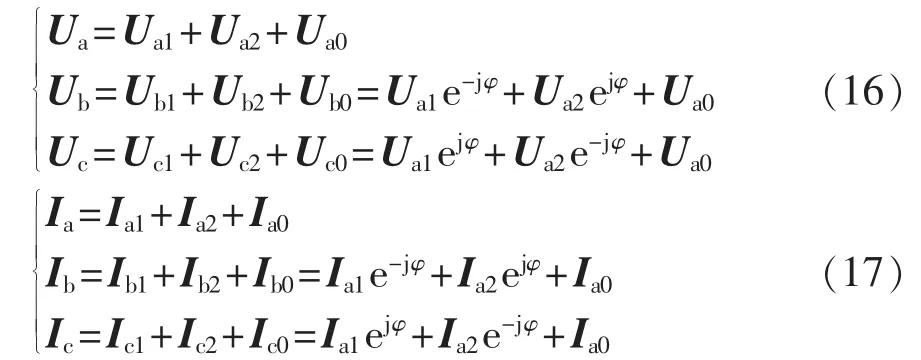
各相功率：

结合式（16）—（18），三相功率求和可得：

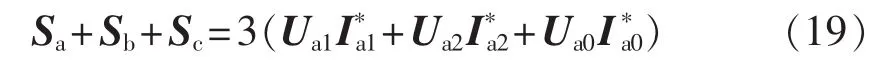
其中，下标 a、b、c 分别表示 a、b、c 相变量；下标 1、2、0分别表示各变量正序、负序、零序分量。

因此，注入功率中负序及零序占的功率比会小于0.25%，分布式电源的注入功率绝大多数是正序功率。PQ控制下分布式电源的功率给定是对称的正序功率，只要控制住分布式电源是正序功率注入就可解决这一矛盾。

本文对不对称电压的处理方法是：测量得到网侧三相电压后求取正序电压，忽略零序分量和负序分量，Dm的相角选择与正序电压一致。这样按本文分布式电源模型计算得到的电流是正序，注入正序电流，即便网侧电压不对称，由于正序电流与负序、零序电压构成的三相功率求和为零，故分布式电源只有正序功率注入。

2.2 初值计算

初值计算作为时域仿真的初始状态，主要是为了求出全系统的各状态量的初值以及动态元件中一些未给定的初始代数量。初值计算以潮流计算为前提，利用稳态潮流得到的代数量进行计算。初值计算正确与否可通过观察各代数量、状态量时域仿真曲线在扰动之前是否是直线来判断。

2.2.1 三相稳态潮流修正

三相时域仿真初值采用三相潮流计算结果，关于配电网的三相潮流计算，不少文献都有研究，方法主要是前推回代法与牛顿法以及2种方法的改进方法。传统三相潮流计算注入点的各相功率都是按照式（16）计算的，由于节点电压的不对称，按此式计算分布式电源的注入电流，即便是对称的三相功率也会得出不对称的电流，分布式电源的注入功率就会包含负序和零序功率，与实际情况不符合，计算得到的初值也不对。

为消除负序和零序功率，在潮流计算中要修正分布式电源的注入电流，只要注入电流为正序，无论注入电压对称与否，注入功率Sia+Sib+Sic只有正序注入功率。由于牛顿法是利用注入功率代替了注入电流得到非线性方程组继而迭代求解，无法直接改变注入电流为正序，本文选择三相前推回代法。

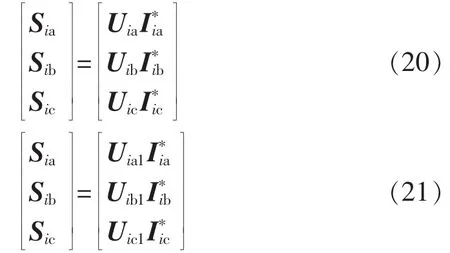
求解注入电流时，负荷节点的注入电流按式（20）求解不变，分布式电源节点的注入电流按式（21）计算，其中Uia1、Uib1、Uic1是各时步迭代式分布式电源节点电压的正序分量。收敛判断时，负荷节点处的功率偏差求解也不变，分布式电源节点利用三相功率求和得到正序功率，与给定三相功率作差得到功率偏差。

2.2.2 各代数量、状态量初值求解

三相潮流结束以后，可以得到分布式电源节点的三相电压、三相注入电流（对称的），求取出网侧电压正序分量、电压正序分量a相电压相角以及电流a相相角，利用Park变换对正序电压ugabc_1和三相对称电流 iabc利用状态量变换，得到 ugd0（ugq0=0）、id0、iq0。

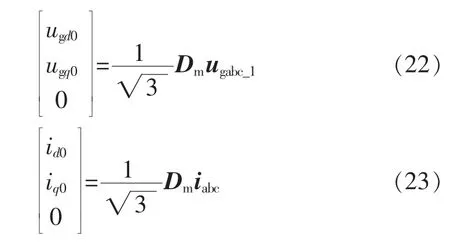
其中，下标0表示初值。

状态量初值求解，利用稳态时状态量是稳定值，从而有状态量的微分为0、PI环节的输入为0，代入微分方程求解。由式（9）有：

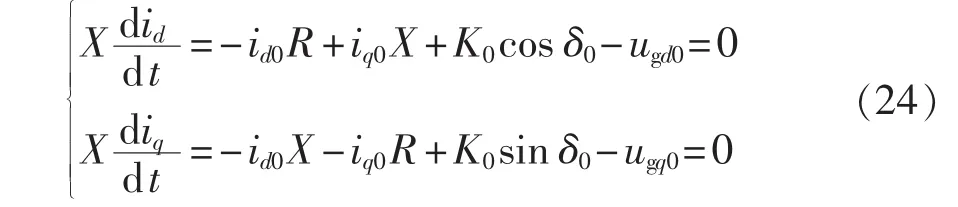
得：

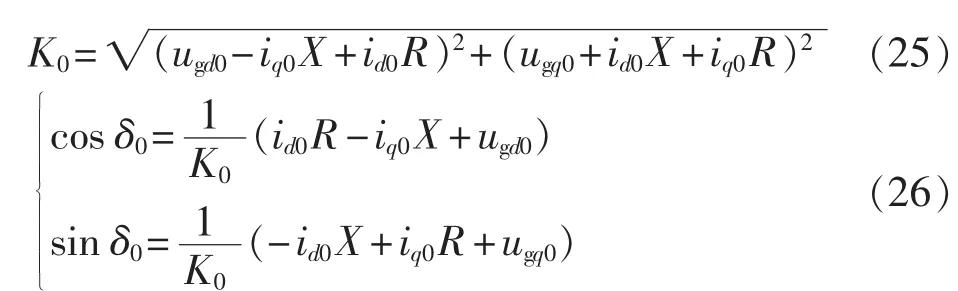
由δ0的正弦、余弦可得其值：

2.3 状态量求解

常见的积分方法分为显式积分与隐式积分方法两大类：隐式积分方法具有良好的数值精度和数值稳定性，常和牛顿法结合使用，突出的问题是隐式积分法编程复杂，牛顿法又需要求解变常数雅可比矩阵，计算速度慢；显式积分方法编程简单、计算速度较快，但也存在交替求解、模型接口带来的迭代误差以及数值稳定性问题。本文采用显式的改进欧拉法，迭代误差通过迭代法进行降低或消除，数值稳定性问题采用降低步长解决。

改进欧拉法包括预测环节和校正环节，具有2阶精度，以下以状态量id和iq的第n+1步值求解为例说明，其余PI环节中存在的状态求解类似。

式（9）得 id、iq的微分方程为：

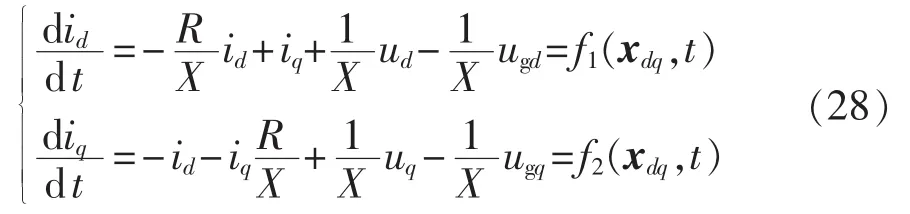
其中，xdq表示 id、iq、ugd、ud、uq变量组。

当已知第n步状态量、代数量时，即已知idn、iqn、ugdn、udn、uqn，预测环节：

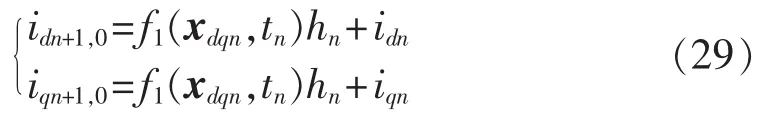
其中，hn为第n步求解第n+1步的步长。

预测环节结束后根据预测得到的所有状态量，进行全网代数量求解，得到xdqn+1，0，再进行校正环节：

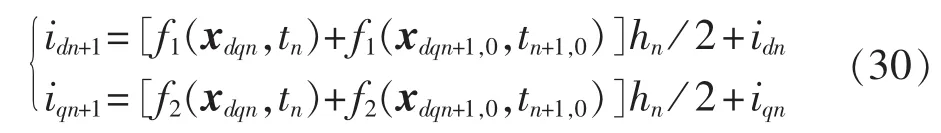
2.4 代数量求解

将负荷看作恒阻抗模型，利用稳态潮流解各相电压值计算出负荷的等效导纳。

将各节点各相导纳并入三相节点导纳矩阵的各相自导纳中。网络采用线性方程，即：

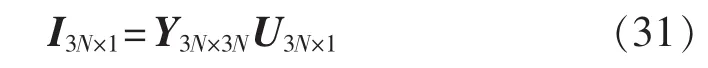
其中，N为节点个数；Y为包括恒阻抗负荷在内等效三相网络节点导纳矩阵。时域仿真过程中，当完成一步状态量求解后，需要进行一步代数量求解，即网络方程式（31）的求解。

各时步恒阻抗负荷节点注入电流为0，存在注入电流的节点有分布式电源节点、平衡节点，当求出各时步以上2种节点注入电流后，可利用式（31）求解得到该时步U。

如果存在静态负荷或异步电动机负荷，则这样的负荷不能并入网络，需要解决各时步负荷的注入电流，而且现有异步电动机负荷也是基于对称模型，可以采用本文分布式电源的不对称问题处理方法类似处理。

2.4.1 分布式电源注入电流求解

分布式电源PQ控制策略模型成立的前提是变换阵Dm始终要与网侧对称的电压相位一致，一则配网中可以包含多个分布式电源，二则在时域仿真各时步中网侧电压相位是不断变化而且不对称的。不对称的问题前已提出采用对称分量法求取正序电压分量，以正序电压分量代替实际网侧电压值，各时步计算时Dm矩阵需要跟踪网侧变化的正序电压相角。

当采用改进欧拉法求解出第n+1步的状态量idn+1、iqn+1，需要进行反 Dm变换得到第 n+1 步 Ia、Ib、Ic，根据式（5）有：

其中，In+1为第n+1步输出电流的有效值；δin+1为第n+1步电流相位超前第n步Dm的相位角。故第n+1步电流有效值为 In+1，a 相相位角为 αn+δin+1（αn是第 n时步各个分布式电源网侧电压正序分量a相相角），以此幅值和相角构造出对称的三相电流，即为分布式电源的三相注入电流。

从上面也可以看出逆变器接口的分布式电源机网接口注入电流求解较为方便，不同于异步电动机、同步电动机等旋转设备，分布式电源网侧注入电流是状态量，不受网侧电压影响，故不存在模型接口误差问题。

综上，分布式电源与网络接口如图6所示。

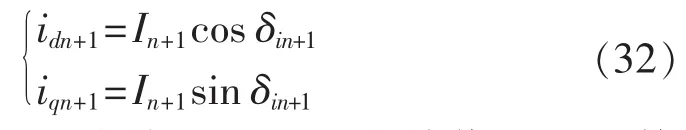
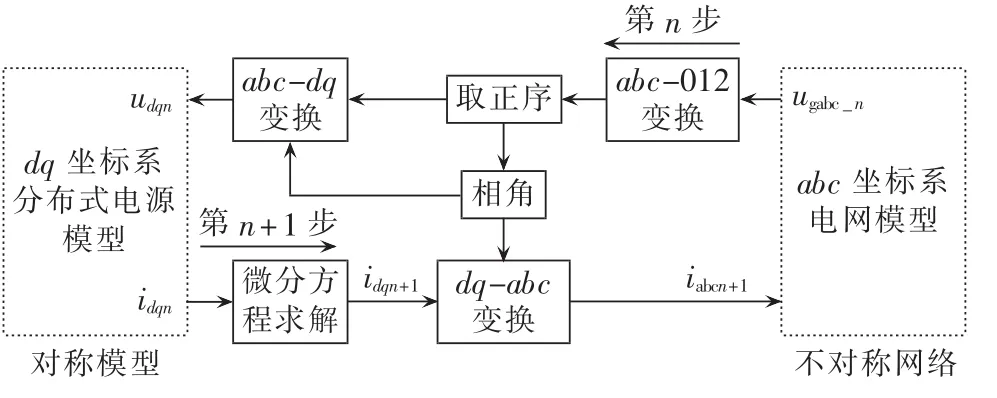
图6 分布式电源与网络接口处理Fig.6 Interfacing between DG and network

2.4.2 平衡节点注入电流

输电网平衡节点是动态元件同步电动机，可以通过机网接口处理方法，得到平衡节点的注入电流。而配电网的平衡节点一般是由上级变压器充当，注入电流不能通过动态元件状态量的求解来解决。但平衡节点在配电网计算中看作电压幅值和相角始终不变的节点，俗称“大电网”，配电网时域仿真各时步平衡节点注入电流需要新的方法求解。

观察式（31），恒阻抗负荷节点注入电流为0，分布式电源注入电流可以求出为已知量，这样电流向量仅有平衡节点的三相电流未知，电压方面，除平衡节点电压已知其他节点三相电压都未知，总3N个未知数，而方程个数也是3N，本质上式（31）仍是线性方程组的求解问题，与常规线性方程组Ax=b不同的是，式（31）左右两侧都有未知数，可以将未知的平衡节点注入电流移到右侧，将已知的平衡节点电压移到左侧，将式（31）转换为Ax=b形式进行求解，限于篇幅，本文不再给出具体求解细节。

2.5 扰动处理

本文考虑的扰动有负荷的突变、分布式电源的投切，其中负荷看作恒阻抗负荷，时域仿真时已经并入网络，突变时只需要修改网络导纳矩阵。分布式电源切除时，置脱网标志位，后续相应的所有代数量、状态量置0处理；分布式电源并网时，并网点电压、相角瞬间获取。所有扰动时，还需要进行一步代数量跃变计算，包括分布式电源内部的代数量跃变。

3 案例测试

3.1 6节点测试算例

构建的配网测试案例如图7所示，取UB=380 V、SB=100 kV·A，线路阻抗、分布式电源参数、负荷功率及扰动信息分别如表1—3所示（考虑四重扰动，分别是DG1投入、节点3负荷突变、DG1功率输出增加、DG2切除）。利用本文的模型及时域仿真方法，编写程序，选取步长为100 μs，仿真结果如图8—11所示，图中电压均为标幺值，后同。从曲线可以看出，投入分布式电源及分布式电源输出功率改变时，功率曲线能较快上升既定目标，波动一段时间后维持稳定，负荷突变及分布式电源切除时，功率曲线变化较小；任何扰动时刻，电压曲线变化明显，其中投入分布式电源和分布式电源输出功率改变时，电压需要经过较长时间维持稳定，负荷变化和分布式电源切除时，电压突变后恢复稳定，速度极快。整体来看，功率曲线能实现给定控制，电压曲线与实际负荷、分布式电源功率水平一致。

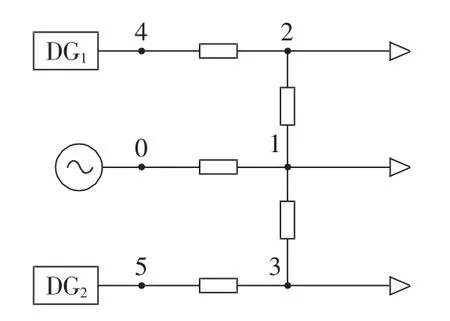
图7 6节点算例Fig.7 6-bus system for test

3.2 IEEE 33节点测试算例

进一步选用IEEE 33节点拓扑作为本文的暂态测试案例，如图12所示，在节点 5、16、22处接入分布式电源，考虑四重扰动下暂态仿真，分布式电源接入及功率信息如表4所示。仿真结束后，选用分布式电源有功功率、无功功率、接入点电压以及负荷波动处电压绘制仿真曲线，如图13—16所示。根据曲线图可发现 0.5 s投入DG3时离 DG3较远的 DG1、DG2输出有功、无功变化很小；2.5 s切除DG1时DG2、DG3的功率曲线几乎无变化；4.5 s节点24负荷突增时DG2、DG3功率曲线也几乎无变化；任何波动时刻，电压曲线变化较明显，但变化幅度非常小，负荷波动时电压突变后恢复稳定，速度极快，分布式电源投切或者输出改变，节点电压曲线需要相对较长时间恢复稳定。整体上四重扰动下，各曲线都能较快恢复到稳态状态，这是由于源节点的Vθ模型很强大，而且相比整个网路的总负荷，3个分布式电源的有功输出只占25%左右（以有功为例，若除去始终接入的DG2，比例只有16%左右），负荷的波动量占11.95%，波动量幅度不是特别大。

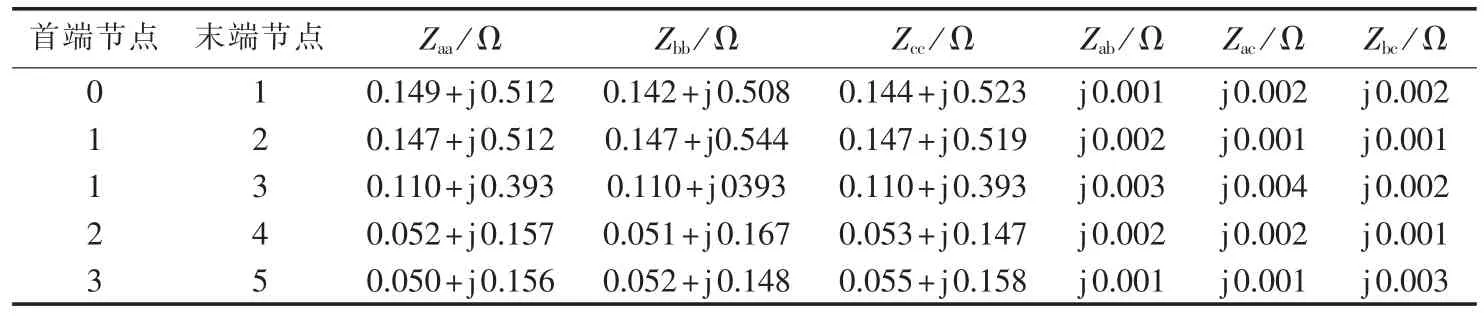
表1 支路数据参数Table 1 Parameters of branches

表2 分布式电源电路及控制器参数Table 2 Parameters of DG circuit and controller

表3 负荷功率及扰动信息Table 3 Information of load power and disturbance

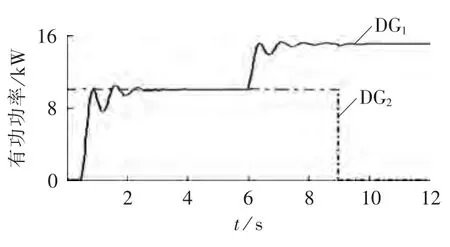
图8 分布式电源有功功率曲线Fig.8 Active power of DGs

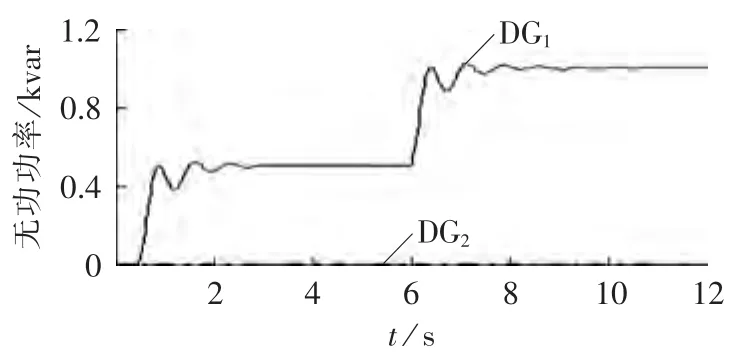
图9 分布式电源无功功率曲线Fig.9 Reactive power of DGs

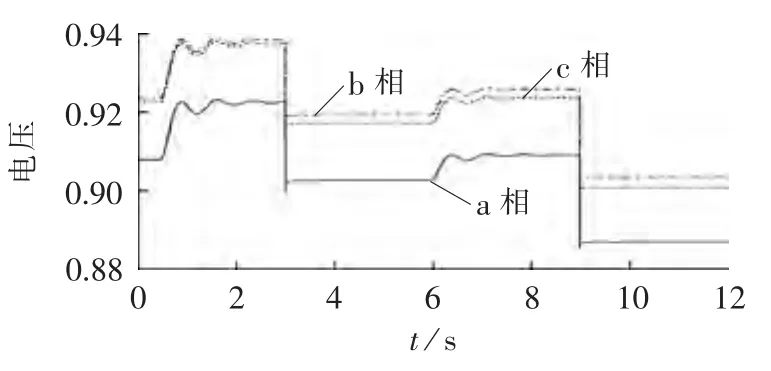
图10 负荷波动点电压曲线Fig.10 Voltage of load fluctuation point

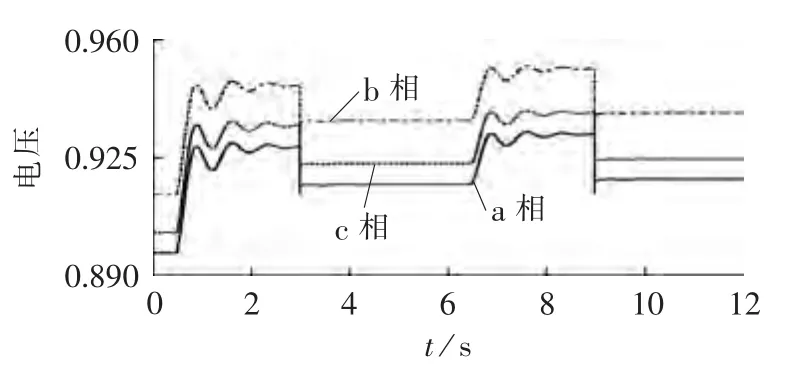
图11 DG1节点电压曲线Fig.11 Voltage of DG1

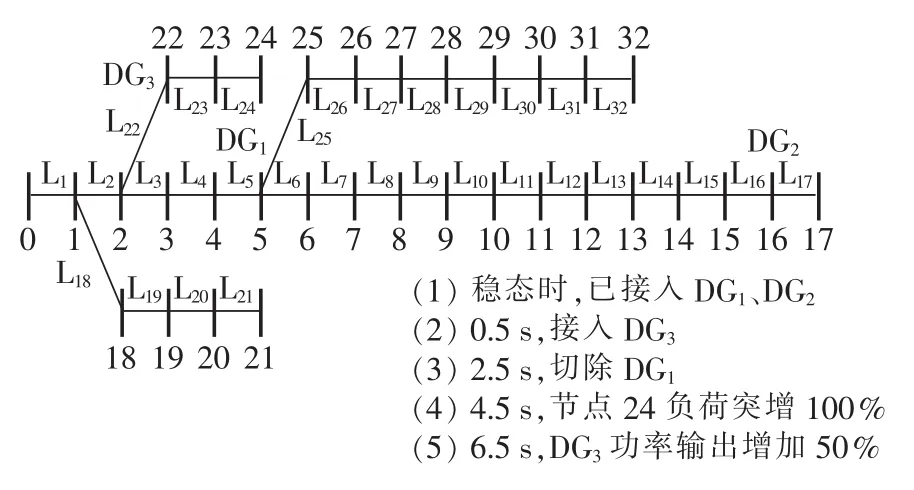
图12 IEEE 33节点算例图Fig.12 IEEE 33-bus system for test

表4 IEEE 33节点系统分布式电源接入及功率信息Table 4 Information of grid-connected DGs and powers of IEEE 33-bus system

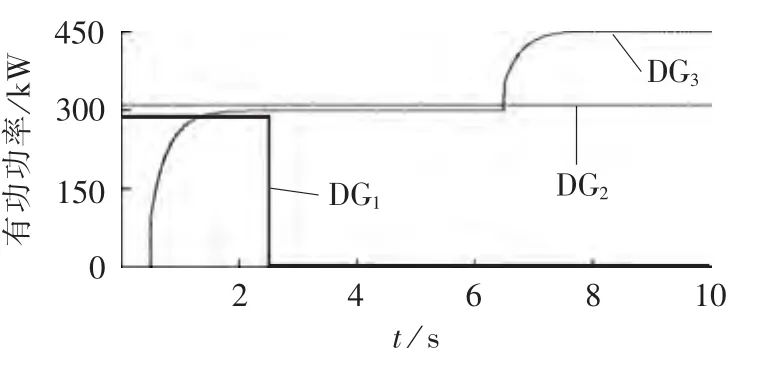
图13 分布式电源有功功率曲线Fig.13 Active power of DGs

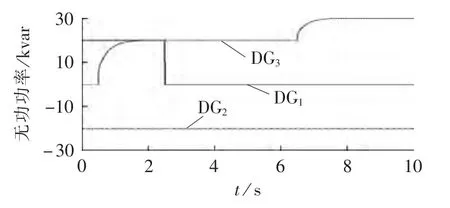
图14 分布式电源无功功率曲线Fig.14 Reactive power of DGs

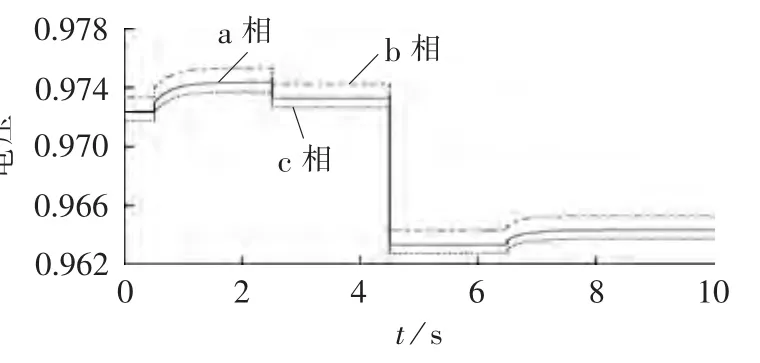
图15 负荷波动点电压曲线Fig.15 Voltage of load fluctuation point

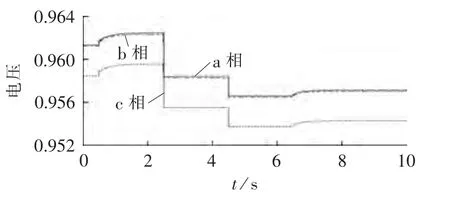
图16 DG1节点电压曲线Fig.16 Voltage of DG1

4 结论

本文提出的配电网三相机电暂态时域仿真以分布式电源为动态元件，解决了分布式电源的电路模型及标幺化、控制器建模，针对分布式电源对称模型与配电网不对称节点电压的矛盾，提出了提取正序分量、Park变换阵跟踪正序分量相角的解决方法，实现了多重扰动下配电网的三相时域仿真，测试案例表明本文的所有理论工作是正确的。不足的是本文并没有对多样的分布式电源源侧进行建模研究，分布式电源的输出特性与实际有一定差距，本文也没有对分布式电源中PI参数的优化进行探索。此外，本文的配电网源节点采用Vθ模型过于理想，不同于输电网的同步机平衡节点模型，同步机也是动态元件，其输出受到最大励磁、原动机最大输入、原动机转动惯量等束缚，不会随意突变，而Vθ模型注入电流、注入功率是代数量，可以瞬间突变进行全系统功率匹配，这也是当恒阻抗负荷突变、分布式电源切除时，电压曲线能瞬间恢复稳定的原因。