基于负荷区域划分的配电变电站规划模型
2015-09-19杜晓东
彭 文,杜晓东,石 敏
(华北电力大学 控制与计算机工程学院,北京 102206)
0 引言
配电变电站规划在配电网规划过程中起着承上启下的重要作用,规划方案的优劣直接影响配电网网络结构、运行维护经济性和供电可靠性。因此,科学合理的配电变电站规划一直是国内外学者研究的重要课题。
近年来,有关配电变电站规划的研究工作取得了长足进步,形成了多种模型和算法。文献[1]提出一种配电变电站参考模型帮助管理者有效地进行投资估计。文献[2]提出一种将电压降、变电站容量等因素考虑进规划模型的变电站选址定容规划模型。文献[3]提出基于改进遗传算法的变电站位置及容量改造与规划方法。文献[4]提出一种结合遗传算法与交替定位分配算法的混合遗传算法解决变电站选址规划问题。文献[5]考虑变电站投资和运行费用以及地理信息对规划方案的影响,建立变电站选址定容模型。文献[6]建立基于区间层次分析法,考虑用地性质、交通情况、防洪排水、地质地貌、施工条件等因素的地理信息因子和变电站建设、运行等费用的变电站规划模型。文献[7]在变电站规划模型中,考虑负荷预测结果误差对规划结果的影响,采用三角模糊数描述负荷的不确定性,并根据投资费用的模糊期望值构造适应度函数。文献[8]提出了变电站选址和定容方法,并采用层次分析法计及地理环境因素对初选变电站的位置进行修正。文献[9]运用启发式和专家系统方法对变电站位置进行规划。文献[10]采用动态规划方法建立变电站的多阶段优化规划模型,决定各阶段所投建的变电站数目、容量类型和供电范围。文献[11]建立基于区间层次分析法,并考虑用地性质、交通情况、防洪排水、地质地貌、施工条件等因素的地理信息因子和变电站建设、运行等费用的综合规划模型。
对上述规划模型进行分析后发现,为了降低问题复杂度,这些规划模型都将网络负荷与配电变电站之间的关系简化为直接相连,忽略了配电变电站出线数量有限的客观实际。文献[12]建立了综合考虑配电变电站规划和配电网线路规划的数学模型,并提出了两层改进的遗传算法与一层最短路算法相互嵌套的求解方法。该模型虽然在一定程度上解决了此问题,但配电变电站规则与线路规划彼此独立,未考虑相互之间的影响。
本文提出一种基于负荷分区的配电变电站规划模型,首先根据网络负荷总量确定合理的出线条数,并采用改进的K-means聚类算法对网络负荷进行区域划分。然后选择一个网络负荷作为整个区域与配电变电站的连接点,该网络负荷称之为源负荷。最后应用果蝇优化算法求解配电变电站的位置,在迭代过程中分2步评价果蝇个体:根据配电变电站的位置为每个分区设置一个源负荷,基于“先主干后支路”原则以源负荷为起始点建立分区内负荷间的网络连接;将分区内网络负荷总量叠加于源负荷,建立配电变电站与源负荷间的放射连接。此外,本文将地理因素引入规划模型,通过惩罚因子与奖励因子来影响规划方案的投资成本,使规划结果更贴近于实际。
1 配电变电站规划模型
配电变电站规划问题可表述为:已知目标年的负荷大小和分布,在满足供电可靠性的前提下,以投资年费用最小为目标,确定待建配电变电站的位置、容量及配电网的结构。
传统的配电变电站规划模型中年费用包括:配电变电站投资与运行年费用;低压侧线路综合投资年费用;低压侧线路网损年费用。其目标函数如下:
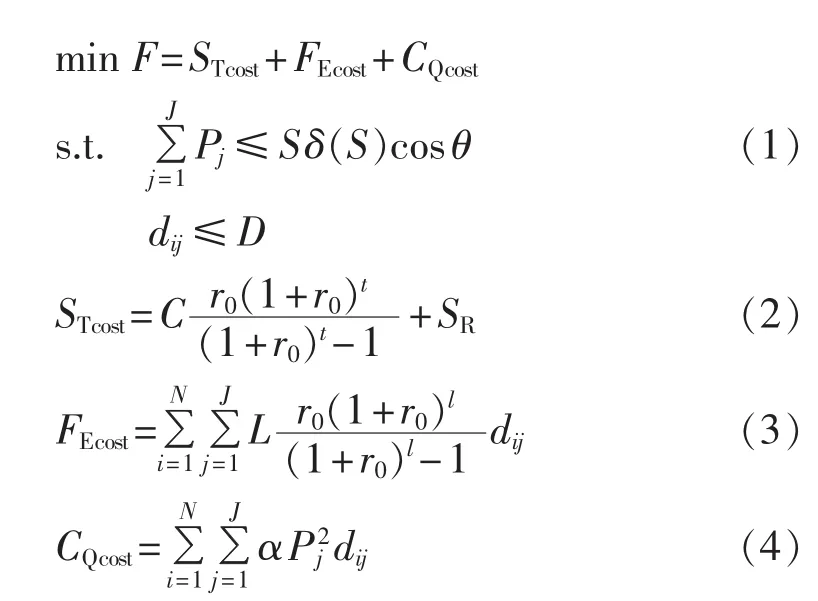
其中,STcost为配电变电站的投资及运行年费用;FEcost为变电站低压侧线路综合投资年费用;CQcost为变电站低压侧线路网损年费用;C为新建变电站的投资费用;r0为贴现率;t为变电站折旧年限;SR为新建变电站的运行费用;N为新建变电站个数;J为网络电负荷数量;L为单位长度线路投资费用;l为变电站低压侧线路折旧年限;dij为变电站i与网络负荷j之间的线路长度, (Xi,Yi)和(lxj,lyj)分别为变电站 i和网络负荷 j位置坐标;α为线路网损折算系数,,α1为单位电能损耗折价系数,α2为线路单位长度电阻,α3为线路年损耗小时数,U为线电压,cos θ为功率因数;Pj为网络负荷的有功功率;S为新建变电站总容量;δ(S)为新建变电站的最大负载率;D为供电半径。
上述规划模型中配电变电站的出线费用和网损年费用仅是估算值,其精确值需要在配电网线路规划后才能得出,因此得到的规划方案往往与预期目标有一定差距。针对此情况,本文将网络负荷划分区域,先对区域内的负荷进行线路规划,然后建立配电变电站与区域之间的连接,同时加入地理优化因子使规划模型更加符合实际。修改后的规划模型为:
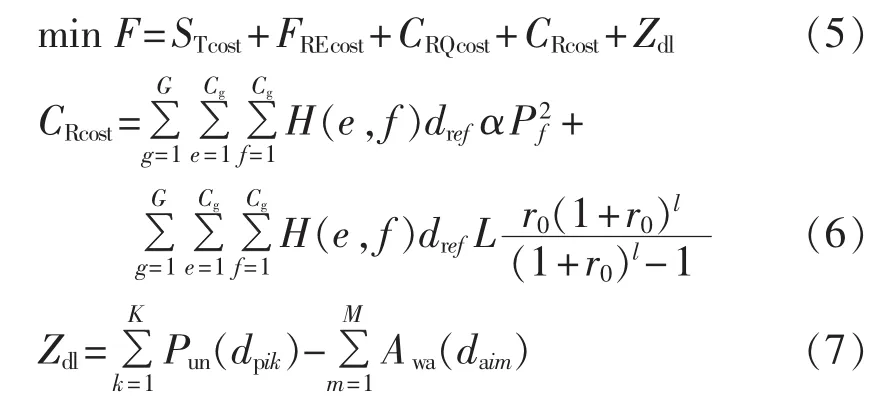
其中,FREcost和CRQcost分别为配电变电站与源负荷间线路的投资和运行年费用;CRcost为区域内线路投资费用和网损费用;Zdl为地理因子;G为区域划分个数;Cg为区域内负荷个数;Pf为负荷f的有功功率;如果负荷e和负荷f之间有连接则 H(e,f)=1,否则H(e,f)=0;dref为负荷 e 和负荷 f之间的线路长度;K为不适宜建站区域总数;M为适宜建站区域总数;dpik为配电变电站i距离不适宜建站区域k的中心距离;daim为配电变电站i距离适宜建站区域m的中心距离。地理因子约束条件可表示为:

其中,Dk为不适宜建站区域k的半径;Dm为适宜建站区域m的半径;Pu为惩罚因子;Aw为奖励因子。
2 模型求解
针对上述规划模型,本文应用负荷区域划分技术和果蝇优化算法求解配电变电站规划方案,规划流程见图1。首先根据合理的配电变电站出线条数对网络负荷进行区域划分,然后将配电变电站的位置视为果蝇群体位置,将式(5)中的投资成本作为浓度判定函数,应用果蝇优化算法迭代更新果蝇群体位置直到发现最优解。在每次迭代中,根据果蝇个体的位置确定源负荷,采用“先主干后支路”原则对区域内负荷进行线路规划,之后建立配电变电站与源负荷的放射状连接,最终将配电变电站和所有线路的投资与运行费用作为浓度判定函数值来引导果蝇趋向食物。

图1 规划模型求解流程图Fig.1 Flowchart of planning model solving
3 负荷区域划分及线路优化
负荷区域划分是在确定配电变电站合理出线条数的基础上,将网络负荷划分为相应数量的互不重叠的区域。在后续应用果蝇优化算法进行配电变电站规划过程中,区域划分结果维持不变,但区域内负荷间的连接关系随着配电变电站位置的改变不断优化。
3.1 确定变电站的出线条数
文献[13]介绍了根据不同线路型号确定配电变电站的出线条数方法,为简化计算,在配电变电站规划中均使用同一型号线路,本文设计的计算公式如下:
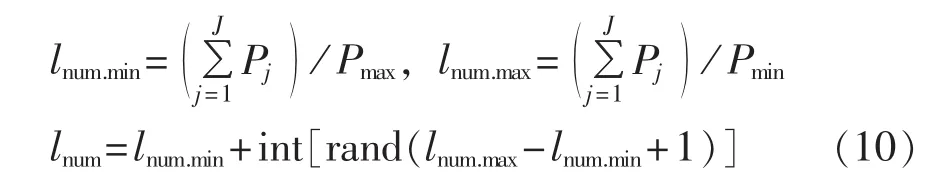
其中,lnum.min、lnum.max分别为出线条数下限、上限值为配电变电站所带区域内所有负荷点的有功之和;Pmax为线路最大有功容量;Pmin为线路最小有功容量;int[·]为对小数取其整数部分;rand 为取[0,1]的随机小数;lnum为配电变电站出线条数。
3.2 基于K-means聚类算法的负荷区域划分
网络负荷区域划分应该满足以下要求:每个区域的负荷总量尽可能均匀;区域内负荷总量不超过配电变电站出线最大容量;各区域间不存在联络线。本文在传统K-means聚类算法[14]中加入分区间负荷转移操作,并将其应用于网络负荷区域划分,步骤如下:
a.在规划范围内随机选择lnum个聚类中心;
b.根据每个网络负荷位置计算其与lnum个聚类中心的距离,把负荷分配到与其距离最近的类中;
c.对每个类中的负荷总量进行计算,并分为高负荷区类和低负荷区类(大于配电变电站出线最大容量的区域称为高负荷区类,未超过配电变电站出线最大容量的称为低负荷区类);
d.选择总负荷最高的区域Cmax,比较与Cmax相邻的2个区域,没有转移出负荷的区域记为Cdes,如果2个区域均未转移出负荷,则负荷总量较低的区域记为Cdes,将Cmax中距离Cdes侧最近的若干负荷转移过去,以保证调整后的区域Cmax属于低负荷区类,并标记Cmax转移出负荷;
e.重复步骤d,使得所有区域均属于低负荷区类;
f.计算重新分配后的聚类中心,执行步骤b,直到聚类中心不再改变,算法结束。
3.3 分区内线路优化
在划分好的负荷区域内,以源负荷为起始点对所有负荷进行线路优化,要求负荷间必须连通且不存在线路跨越。本文参照已有众多实际配网线路走向,提出“先主干后支路”的连接原则,在配电变电站位置 Ps0=(X0,Y0)确定后,一个负荷区域内 r个网络负荷{Ps1,…,Psj,…,Psr}的线路优化流程如下:
a.计算负荷区域内距离配电变电站Ps0最近的网络负荷,记为源负荷Ps*=(X*,Y*),线路集合;
b.找到距离源负荷Ps*最远的负荷点P*s,标记负荷 Ps*和 P*s;
c.令Q=Ps*,将P*s和所有未标记的负荷构成集合 U={Psi},计算 Psi与 Q 之间的距离 Di1,Psi与直线之间的距离 Di2,记 Ps=min(Di1+Di2),标记负荷Ps并将连接添加到集合E,更新Q=Ps;
d.重复执行步骤c,直到Ps=P*s;
e.对所有未标记的负荷Psi,计算已标记的负荷中与其距离最近的负荷P*si,距离为Di,令Psm为所有距离Di中最小数值对应的负荷,标记负荷Psm并将添加到集合E;
f.重复执行步骤e,直到区域内所有负荷标记完毕,集合E即为该区域的线路优化结果;
g.根据集合E计算CRcost得出负荷分区内的投资和运行年费用。
图2是一个具有9个网络负荷的区域,其中0点为源负荷,线路优化结果更贴近于实际情况。
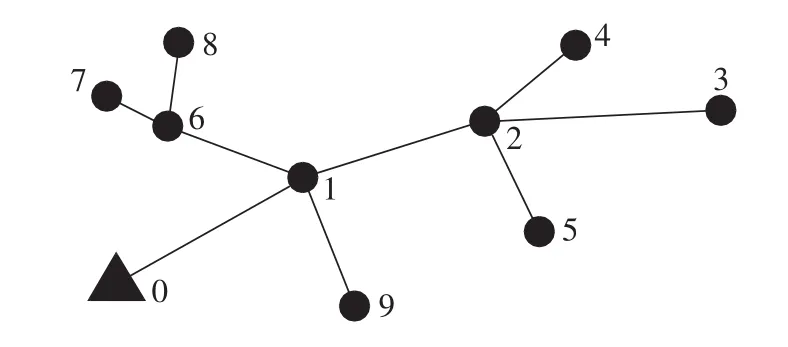
图2 负荷区域内线路优化结果Fig.2 Result of line optimization in load region
4 基于果蝇优化的配电变电站规划算法
4.1 果蝇优化模型
果蝇优化算法[15]是最近提出的一种基于果蝇觅食行为的全局优化方法,已引起广大学者的关注[16-17]。果蝇在感官知觉上优于其他物种,尤其是在嗅觉和视觉方面,该性能使果蝇能很好地搜集飘浮在空气中的各种气味,然后飞近食物位置后亦可使用敏锐的视觉发现食物与同伴聚集的位置,并往该方向飞去。
依据果蝇搜索食物的特性,果蝇优化算法可归纳为以下步骤。
a.给定群体规模psize、最大迭代数gmax,随机初始化果蝇群体位置 Pos0=(Pos0x,Pos0y);
b.赋予每个果蝇个体利用嗅觉搜寻食物的随机方向与距离:
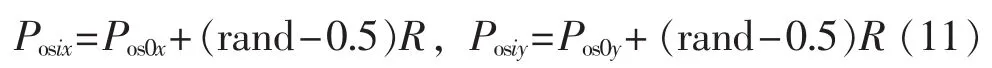
其中,R为搜索半径。
c.由于无法得知食物位置,故先估计与原点的距离di,再计算味道浓度判定值Si,其为距离的倒数。
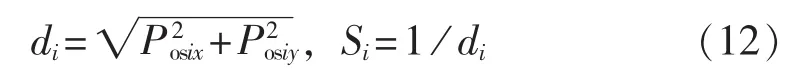
d.将Si代入味道浓度判定函数(亦为适应度函数),用来求出果蝇个体位置的味道浓度ρsi:

e.找出群体中味道浓度最高的果蝇(最优个体):

f.记录并保留ρsbest对应的个体Posbest及相应的坐标,此时果蝇群体利用视觉向该位置飞去。

g.进入迭代寻优,重复执行步骤b—e,直到迭代次数大于gmax或最优味道浓度不再变化。
4.2 基于果蝇优化的配电变电站规划求解算法
本文讨论的配电变电站规划属于单源规划问题,只需确定配电变电站的最优位置,这与果蝇个体搜索食物过程非常相似。可将果蝇个体表示为配电变电站位置,则果蝇优化算法的搜索空间由所有可行的配电变电站位置组成。在搜索过程中,配电变电站规划的投资成本作为味道浓度判定函数,将果蝇个体的位置代入判定函数中可以计算出投资成本,数值越低则味道浓度值越高,果蝇个体越优秀。将果蝇优化模型应用于配电变电站规划的步骤如下。
a.参数设置。其中,果蝇优化算法涉及的参数有果蝇种群规模大小和迭代次数;规划模型中用到的参数包括贴现率、折旧年限、线路单位长度投资费用、网损折算系数、惩罚因子和奖励因子。
b.应用3.1节方法计算配电变电站出线条数,采用3.2节方法对网络负荷进行区域划分。
c.初始化果蝇群体位置,理论上该位置距离最优解越近越好,因此本文将所有网络负荷的加权质心作为群体初始位置,即:
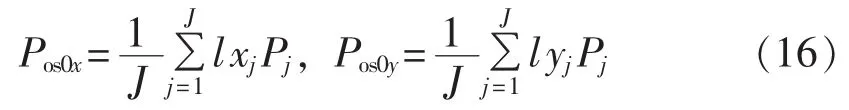
d.设置果蝇个体的随机方向和距离,并计算相应的浓度判定函数。针对每个果蝇个体,先根据其所在位置找到各负荷区域的源负荷,以此为起始点应用3.3节方法建立区域内线路连接;再以式(5)作为浓度判定函数评价个体,数值最小的为最优个体。为应用果蝇优化模型,将浓度判断函数F变换为Si的映射。
F 原定义为 F=F(Xi,Yi) =STcost+FREcost+CRQcost+CRcost+Zdl,而,定义 φ=arctan(Yi/Xi),其中(Xi,Yi)为配电变电站位置,由定义可知:
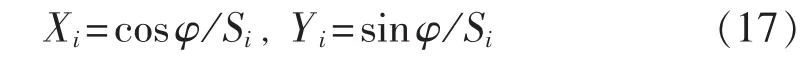
这样浓度判定函数变为:

e.应用果蝇优化模型执行迭代过程,直到满足结束条件,所得最优解即为配电变电站的最佳位置。
5 算例及结果分析
5.1 算例设计
根据电网发展规划,某地区计划建一座35 kV的变电站,年负荷预测结果为13630 kW,根据规划导则要求。35 kV变电站容载比为1.8,则可确定规划年变电站总容量至少为24543 kV·A,则规划变电站的规模方案为3×16MW,已知该地区共有32个负荷点,如图3所示,其中特殊地理区域范围如表1所示。
应用本文所提配电变电站规划模型,设置贴现率r0为0.08,折旧年限t为16 a,线路单位长度投资费用L均为150万元/km,网损折算系数α=0.00469(假设线路全年投入运行),果蝇群体初始位置为以所有网络负荷的加权质心为中心的[-2,2]km区间,迭代过程随机飞行方向与距离区间为[-1,1]km,果蝇种群规模大小为30只,迭代次数为100,惩罚因子为100,奖励因子为100。规划结果见图3,所有的负荷被划分为6个区域,可见规划结果更符合实际。

图3 本文配电变电站规划结果Fig.3 Result of substation planning by proposed method

表1 特殊地理区域Table 1 Specific geographic regions
5.2 算法分析
本文的规划模型中负荷区域划分是至关重要的环节,也是与传统规划模型的区别所在。如果区域划分个数过多甚至等于网络负荷个数,那么本文模型将退变为传统规划模型。因此合理的区域个数对规划结果影响较大,为此针对5.1节中的算例,分别选取区域个数从6到10进行重复实验。结果显示随着区域个数的增多,区域内负荷间线路减少,变电站与源负荷间线路增多,但其线路长度远大于负荷间线路长度,所以投资成本增加。
惩罚因子和奖励因子体现了地理区块是否适宜建设配电变电站,其数值大小直接影响变电站位置的选择。过分强调奖励因子的作用则导致规划位置必定落入适宜建站区域,同样过大的惩罚因子将规划位置排除在不适宜区域。若出现这种情况,寻优策略的效果将大打折扣。相反地,如果降低其比重,则失去了地理信息对规划结果的导向作用。通过大量实验结果分析,惩罚因子和奖励因子取值都为100时,优化过程兼具自由度和倾向性。
在果蝇群体寻优过程中,搜索区间的范围制约着寻优速度和最优结果。如果搜索区间过大会覆盖整个规划区域,果蝇群体会变为随机搜索,很难发现最优解;而搜索区间过小,果蝇搜索时间将会增加,且容易陷入局部最优。本文选取搜索区间从[-1,1]km到[-5,5]km,针对每个搜索区间分别执行10次规划过程,算法平均执行时间和获得最优投资费用见图4,从图中看出区间[-2,2]km是一个较为理想的选择。
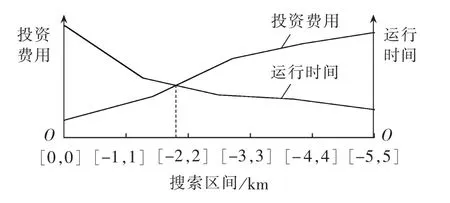
图4 搜索区间对投资费用和运行时间的影响Fig.4 Influence of search scope on investment and search time
5.3 结果对比
为说明本文规划模型的有效性,基于5.1节算例分别实现文献[12]和文献[18]中的规划模型。文献[18]的规划模型不仅包含以往的变电站选址定容模型问题中可量化的因素,还将地理信息约束作为惩罚因子融合入模型中,增加了变电站选址模型的实用价值,规划结果见图5。由于采用放射状连接,规划方案中变电站位置更趋向于网络负荷的加权质心位置。
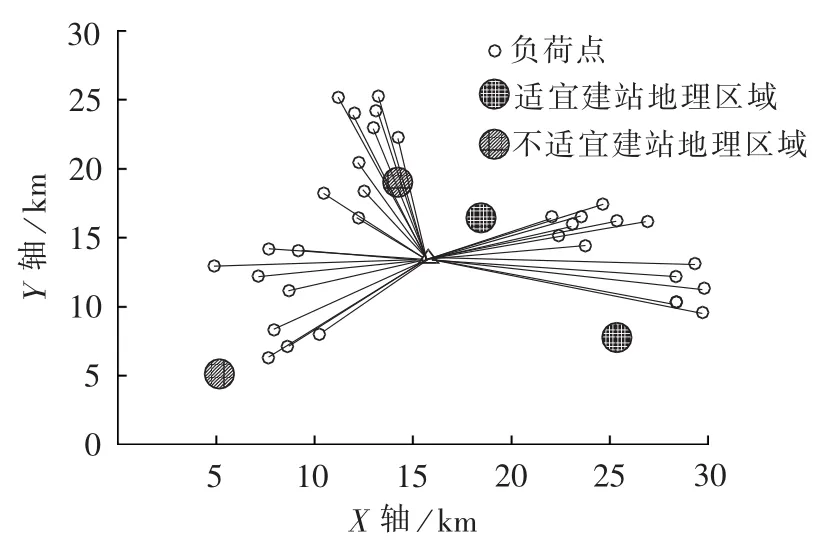
图5 文献[18]配电变电站规划结果Fig.5 Result of substation planning by method in reference[18]
而文献[12]利用改进的遗传算法与经典的最短路算法之间的嵌套调用,重点是确定最优线路规划方案,对于变电站规划只是计算候选站址的优劣。图6是对随机生成10个变电站候选站址计算后得到的最优规划方案,结果显示较之放射连接有所改进,但模型中未考虑出线数量和站址寻优环节,且线路连接方式受站址影响较大,分支数量的确定缺少明显理论依据。表2是3种算法的规划结果对比,从中可发现本文的规划方案投资费用更加合理,网架结构更接近于实际情况。虽然本文规划过程相对比较复杂,但快速的果蝇优选算法框架很大程度上弥补了该不足。
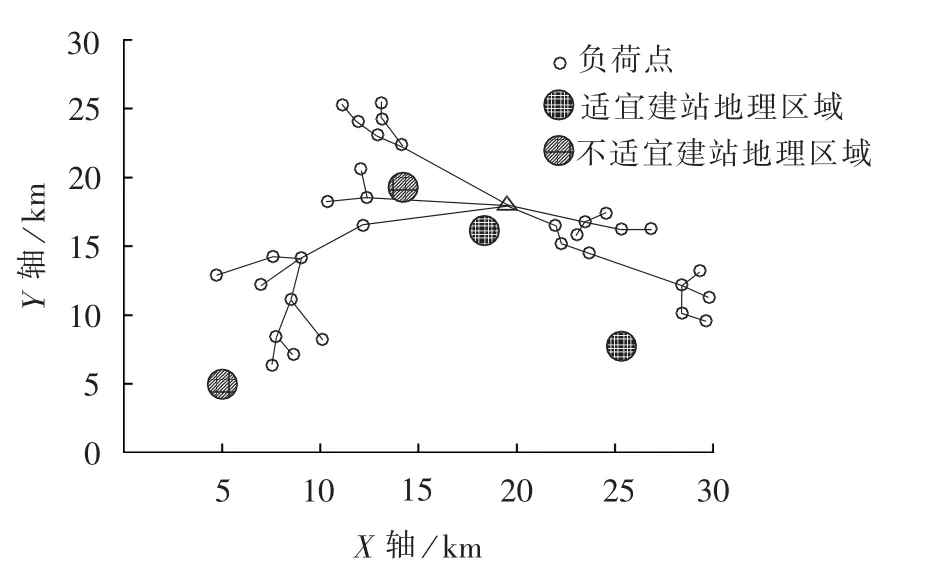
图6 文献[12]配电变电站规划结果Fig.6 Result of substation planning by method in reference[12]
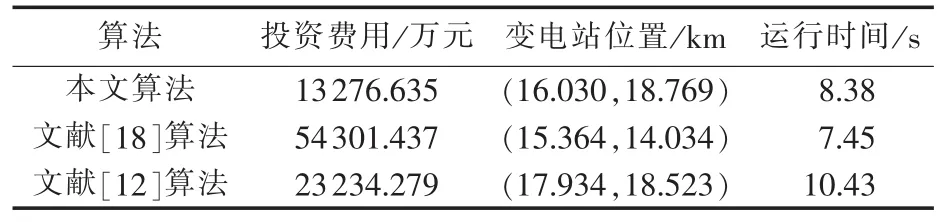
表2 规划结果比较Table 2 Comparison of planning results
6 结论
配电变电站规划是一个多约束、多目标、大规模、非线性的组合优化问题,本文针对现有规划模型中存在变电站出线数量和网络负荷数量不匹配的缺陷,提出一种基于负荷区域划分的配电变电站规划模型,并将改进的果蝇优化算法应用于求解过程。通过对算例结果分析,得出如下结论:
a.基于负荷区域划分的配电变电站规划模型更贴近实际需求,区域内的线路优化采用“先主干后支路”的方法,最大限度地贴近实际规划原则;
b.将果蝇优化算法引入配电变电站规划问题中,充分发挥其计算速度快、全局寻优能力强、具有较好的综合寻优性能等优势;
c.配电变电站规划模型考虑了建站投资、站区线路投资、区内线路投资和网络运行费用对站址选择的影响,结合了地理信息,使规划方案更科学、合理。
