基于电源电流和负载电流检测的前馈加反馈的三相四线制APF控制策略
2015-09-19梁营玉刘建政许杏桃杨奇逊
梁营玉,刘建政,许杏桃,杨奇逊,王 一
(1.华北电力大学 新能源电力系统国家重点实验室,北京 102206;2.清华大学 电力系统及发电设备控制和仿真国家重点实验室,北京 100084;3.江苏省电力公司电力科学研究院,江苏 南京 211100)
0 引言
由于感应电机和非线性负载的大量应用,工业用户通常存在功率因数低、谐波污染严重等问题。对于接入电网的工业用户,电力公司对其功率因数和谐波含量有严格的标准,工业用户常采用电容器组和无源滤波器进行功率因数的校正和谐波的治理。但电容器组不能实现无功功率的无级差调节且动态特性差;无源滤波器常由于设备老化导致滤波效果变差,且容易引起谐振问题[1]。
三相四线制有源电力滤波器(APF)不存在上述问题,并且可以补偿无功功率、各次谐波电流、零序电流以及三相电流的不平衡分量,因此其应用越来越普遍。根据谐波电流的检测点不同,其控制策略可分为以下3种:检测负载电流进行前馈(开环)控制[2-4];检测电源电流进行反馈(闭环)控制[5-7];同时检测负载电流和电源电流进行前馈加反馈的控制策略。第1种控制策略是开环控制,简单可靠、响应速度较快,但易受互感器检测精度、测量延时、DSP计算延时、电流控制延时及负载电流谐波分量预测准确度等因素的影响,补偿效果往往难以满足要求;第2种控制策略是闭环控制,控制精度较高,可以消除测量精度、计算延时和电流跟踪等环节带来的误差,但其控制复杂,响应速度慢于开环控制,不能应用于快速变化的非线性负荷;第3种控制策略是将开环和闭环控制相结合,兼顾控制精度和响应速度,效果较理想。本文采用第3种方法,其中闭环部分采用多个同步旋转坐标系下的积分调节控制,可以消除各次谐波、无功分量、零序电流和三相不平衡分量,并且具有良好的动态特性,通过仿真和实验验证了其有效性。
1 谐波电流的检测
谐波电流的检测是APF进行谐波补偿的前提和关键,谐波检测的好坏直接影响谐波补偿的效果。目前用于谐波电流检测的方法很多,如基于频域傅里叶变换的方法[8]、基于自适应噪声对消原理的方法[9-11]、基于小波变换的时变检测法[12-13]、基于瞬时无功功率理论的检测方法[14]。其中,基于瞬时无功功率理论的p-q法和ip-iq法应用最为广泛并取得较好的效果。然而,p-q法在系统电压非正弦情况下存在较大的检测误差;ip-iq法在三相电压不对称时不能准确地检测电流中的无功分量且仅适用于三相三线制系统[2]。本文提出一种新型谐波电流检测法,可以检测三相四线制系统的任意次谐波的正、负、零序分量及无功分量,原理框图如图1、2所示。
1.1 n次谐波各分量的检测[15]
n次谐波的正序dq变换实质是将abc静止坐标系转换为以角速度nω0沿a-b-c方向旋转的dq坐标系。三相电流经过变换矩阵为Tn+abc-dq的n次正序dq变换,则n次谐波的正序分量变为直流量,其余各次谐波及其各分量均为交流量,经过低通滤波器(LPF)滤除交流分量,再经过变换矩阵为Tn+dq-abc的n次正序dq反变换,即可得到n次谐波的正序分量。

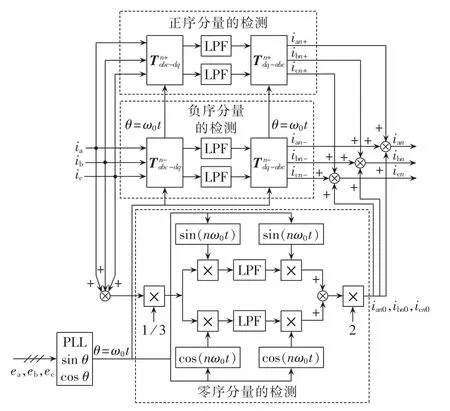
图1 n次谐波电流检测的原理框图Fig.1 Schematic diagram of nth harmonic current detection

图2 无功分量的检测原理框图Fig.2 Schematic diagram of reactive component detection
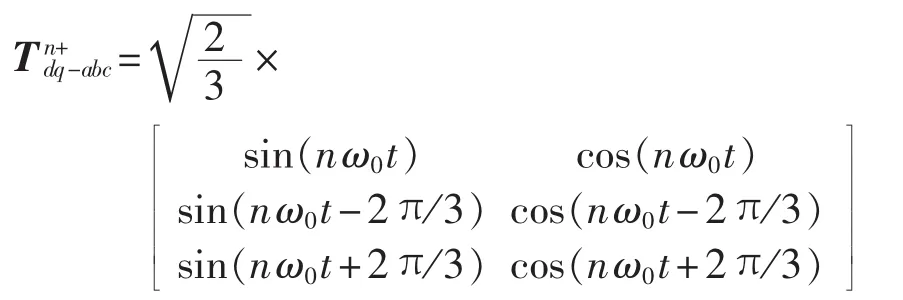
n次谐波的负序dq变换实质是将abc静止坐标系转换为以角速度nω0沿a-c-b方向旋转的dq坐标系。n次谐波负序分量的检测方法原理同正序。将矩阵 Tn+abc-dq和 Tn+dq-abc中的 2π/3全部换成-2π/3,-2π/3全部换成2π/3,即可得到 n次负序 dq坐标变换矩阵Tn-abc-dq和反变换矩阵Tn-dq-abc。
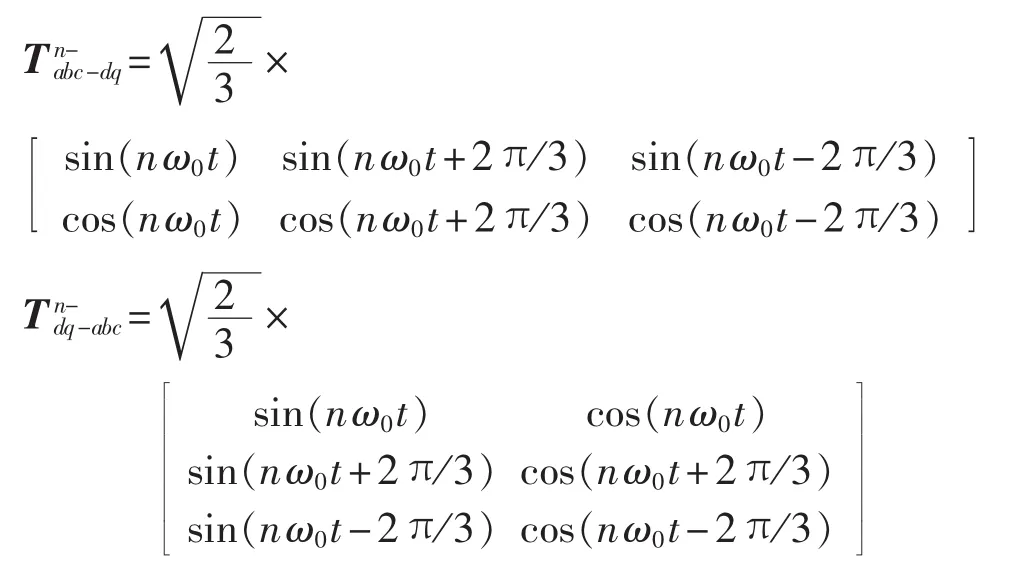
零序分量的检测与正、负序电流稍有不同。由于零序电流的特殊性,不能采用三相dq坐标变换将其转化为直流量。根据零序电流的定义,零序电流为(ia+ib+ic) /3=ia0=ib0=ic0,等于 abc 三相中任意相上所有次谐波零序分量之和。令x(t)代表零序电流,即x(t)=ia0。 待检测信号 x(t)与参考正弦信号 sin(nω0t)和余弦信号cos(nω0t)相乘,可以将n次谐波转换为直流量和2n次谐波两部分,如下式所示:

对式(1)、(2)作傅里叶变换,得:

由式(3)、(4)可知,零序电流 x(t)与正弦和余弦信号相乘相当于将零序电流的频谱平移nω0和-nω0(并乘以系数1/2),则零序电流的n次谐波分量转换为直流量和2n次分量,其余次谐波分量仍为交流量[13]。 用低通滤波器滤除 xd(t)和 xq(t)中的交流量,得到直流量 Xd(0)和 Xq(0)。 零序电流中的 n次谐波分量为:
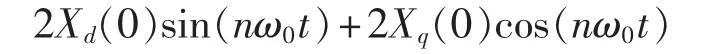
上述方法不仅可以检测各次谐波的零序分量,还可用于单相系统中任意次谐波的检测。
1.2 无功电流的检测
基波负序、零序分量的检测与谐波分量的检测原理相同,无功分量的检测略有不同,检测方法如图2所示。检测无功分量需要先确定基波正序电压的相位即θ+,经过dq变换得到的q轴分量即为无功分量。
无功分量检测的关键在于基波正序电压相位的获取,本文采用图3所示的锁相方法[16]。

图3 软件锁相原理框图Fig.3 Schematic diagram of software PLL
若 uq=0,则相位无误差;若uq≠0,则表明相位有误差,且uq的大小反映相位误差的大小。将uq归一化后,通过超前/滞后校正环节的输出作为角频率的误差,用来修正初始角频率ω0。达到稳态时,输出的相位即为输入电压基波正序分量的相位。超前/滞后校正环节具有良好的滤波作用,可以有效滤除基波负序电压反映在dq坐标系的2次谐波分量及其他各次谐波分量,因此锁相环的输出为基波正序电压的相位。
2 同时检测电源和负载电流的前馈加反馈选择性补偿控制策略
为了兼顾系统的控制精度和动态性能,本文同时检测电源电流和负载电流,对电源电流进行反馈控制,对负载电流进行前馈控制,原理如图4所示。
前馈控制即检测负载电流,分别提取各次谐波的正、负、零序分量得到指令电流,然后采用无差拍控制使APF发出的实际电流在一个开关周期结束时跟踪上指令电流。反馈控制即在多个同步旋转坐标系下对电源电流各次谐波的正、负、零序分量的误差信号进行积分调节(如图5所示),得到各次谐波的指令电流,然后采用无差拍控制使APF发出的实际电流在一个开关周期结束时跟踪上指令电流。前馈加反馈的控制方式即前馈控制得到的指令电流和反馈控制得到的指令电流相加得到总指令电流再采用无差拍控制,使APF实际发出的电流准确跟踪总指令电流以消除电源电流中的各次谐波。前馈控制保证了动态响应速度,反馈控制保证了控制的精度。
对于采用无差拍控制的数字控制系统,从信号采样到PWM信号的输出存在一个控制周期的延时,无差拍的控制方式本身存在一个控制周期的延时,因此,在进行图1和图2的坐标反变换时,应考虑2个控制周期的延时,并对该延时补偿,补偿方法见文献[2]。
2.1 n次谐波各分量的闭环控制
n次谐波各分量的闭环控制策略如图5所示。n次谐波正、负、零序分量在各自同步旋转坐标系中为直流量,积分环节在零频率处的增益为无限大,因此积分器可以对直流量实现零稳态误差的控制。由于被测电流为电源电流,因此各次谐波各分量的参考值设为0。由于积分器的作用,达到稳态时电源电流各次谐波跟踪上参考值0,从而消除了电源电流中的各次谐波。积分器本身具有滤除谐波的作用,避免了使用低通滤波器带来的延迟和对系统稳定性的影响[17],提高了控制系统的动态性能和稳定性,同时减少了DSP的计算量。

图4 前馈加反馈控制策略的原理框图Fig.4 Schematic diagram of feedforward-feedback control strategy
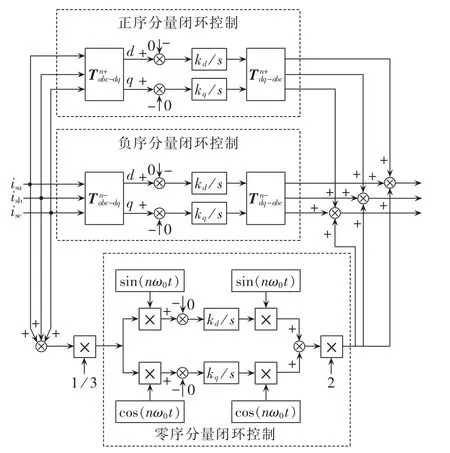
图5 n次谐波电流的闭环控制框图Fig.5 Schematic diagram of closed-loop nth harmonic current control
2.2 无功电流的闭环控制及电容电压的控制
基波负序和零序闭环控制方法与n次谐波闭环控制方法原理相同。无功分量及电容电压的控制策略如图6所示。

图6 无功分量及电容电压控制策略框图Fig.6 Schematic diagram of reactive component andcapacitor voltage control
通过基波正序dq坐标变换得到dq分量,其中d轴分量为有功分量,q轴分量为无功分量。对q轴分量进行积分调节补偿无功分量(可根据功率因数的要求调整无功电流的指令值Iqref),通过改变d轴分量大小调节电容电压稳定在参考值。
3 仿真分析
采用 PSCAD/EMTDC对上述控制策略进行仿真分析,仿真参数为:开关频率为10 kHz;三相连接电感为0.3 mH;中线连接电感为0.1 mH;直流电容为15000 μF;负载为非线性不平衡负载,采用直流侧为4 Ω电阻的三相不可控整流桥负载,c相与N相间接有7 Ω电阻的不平衡负载。
图7为3种控制策略下,a相电源电流总谐波畸变率 THD(Total Harmonic Distortion)的变化(APF在0.2 s投入运行)。从3幅子图的对比可以看出,前馈控制和前馈加反馈控制具有较快的响应速度,反馈控制响应速度较慢。前馈控制下,a相电源电流的THD由26%下降到5.2%;反馈控制下,a相电源电流的THD由26%下降到1.7%;前馈加反馈控制下,a相电源电流的THD由26%下降到1.5%。反馈控制和前馈加反馈控制滤波效果均优于前馈控制。图8进一步说明了前馈加反馈控制滤波效果的优越性。由此可见,与其他2种控制策略相比,前馈加反馈控制同时具有良好的补偿效果和动态性能。

图7 3种控制策略下a相电源电流THD的变化Fig.7 Variation of phase-a source current THD for three kinds of control strategy
谐波检测的准确性是进行谐波补偿的基础和前提,因此图9和图8(c)中的各次谐波和无功分量的补偿效果间接表明:新型谐波电流检测法可以准确检测三相四线制系统中的任意次谐波分量及无功分量。从图9中可以看出,基于前馈加反馈控制策略的三相四线制APF可以有效滤除三相电源电流中的谐波分量、三相不平衡分量、中线零序电流及无功分量。

图8 a相电源电流频谱图Fig.8 Spectrum of phase-a power current
4 实验分析
为验证所提出的控制策略,在130 kV·A的实验平台上进行物理实验,实验条件如下:交流线电压380 V,直流电容电压750 V,开关频率10 kHz,直流电容 15000 μF,LCL 滤波器 0.165 mH、0.03 mH、50 μF、0.75 Ω,死区时间 3 μs。 主控制器为数字信号处理器TMS320F28335,波形录入采用录波仪DL850和电能质量分析仪FLUKE435。
图10为负载突变时3种控制策略动态响应速度的对比波形,3种控制策略的响应时间标注在图中。非线性负载发生突变时,前馈控制和前馈加反馈控制的响应时间均为1个工频周期左右,而反馈控制的响应时间为6~7个工频周期。与其他2种控制策略相比,反馈控制的响应速度较慢,不能用于快速变化的非线性负荷的补偿。
图11(a)和 11(b)分别为未进行谐波补偿和仅补偿5次谐波后的电源电流频谱图。5次谐波的谐波含量从补偿前的22.6%下降至0.4%,THD从补偿前的26.9%下降至14.3%,由此可见,本文提出的单次谐波检测和控制策略可以有效补偿特定次谐波。

图9 三相电源电流、中线电流及a相电源电压波形Fig.9 Waveforms of three-phase source current,neutral current and phase-a source voltage
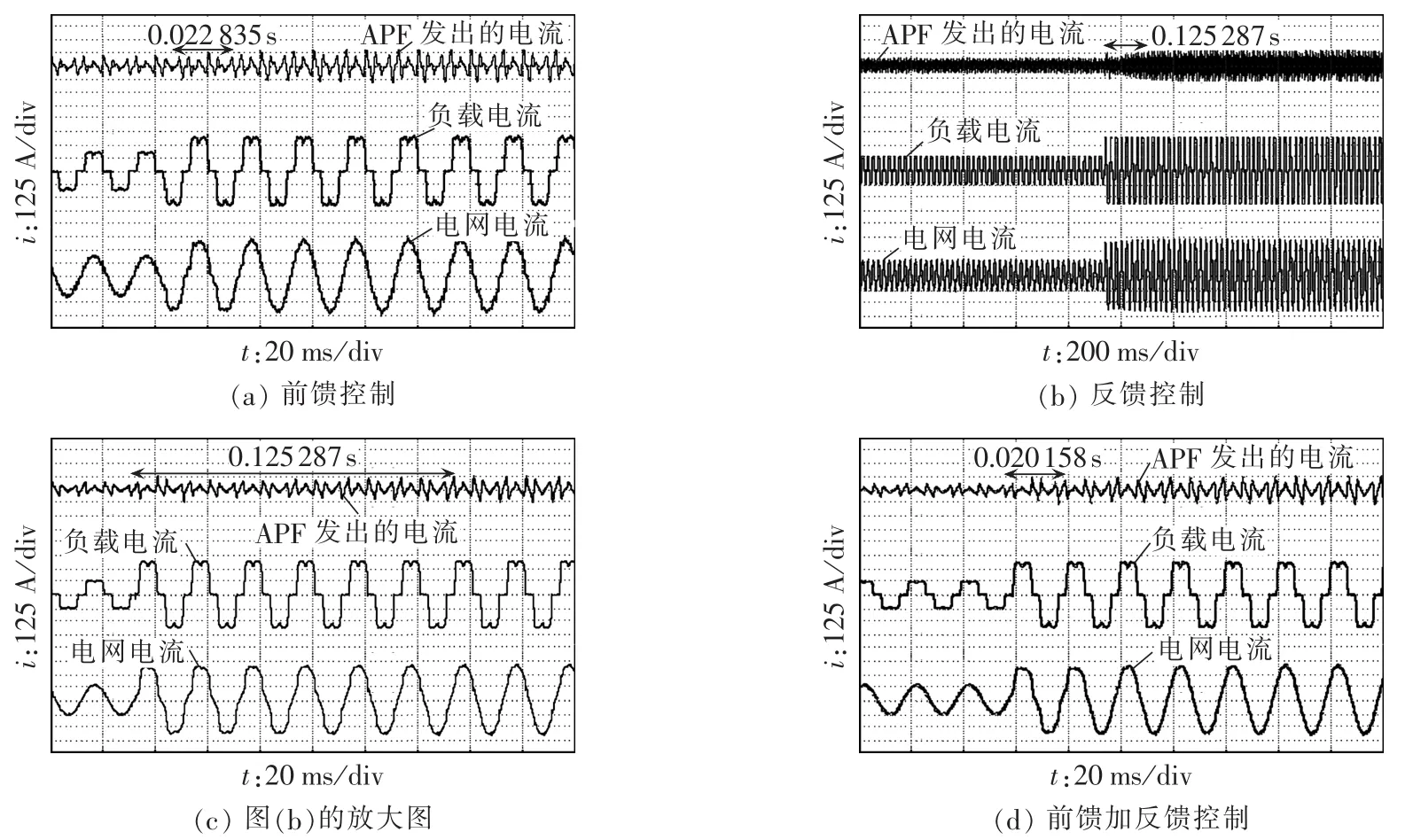
图10 3种控制策略动态性能的对比Fig.10 Comparison of dynamic performance among three kinds of control strategy

图11 电源电流频谱图Fig.11 Spectrum of source current
图12为3种控制策略在稳态性能上的对比,以谐波补偿后电源电流的稳态THD为考核指标。3种控制方式的THD分别为5.1%、3.5%、3.2%,反馈控制和前馈加反馈控制的稳态性能优于前馈控制。
谐波检测的准确性直接影响谐波补偿的效果,图12(c)和图13进一步表明:新型谐波检测法可以精确检测三相四线制系统的各次谐波分量和无功分量。从图13可以看出,基于前馈加反馈控制策略的三相四线制APF可以有效补偿非线性负载产生的各次谐波、三相不平衡、中线零序电流和无功分量(用电能质量分析仪测得图13(c)的功率因数为0.98,图13(d)的功率因数为 1.0)。
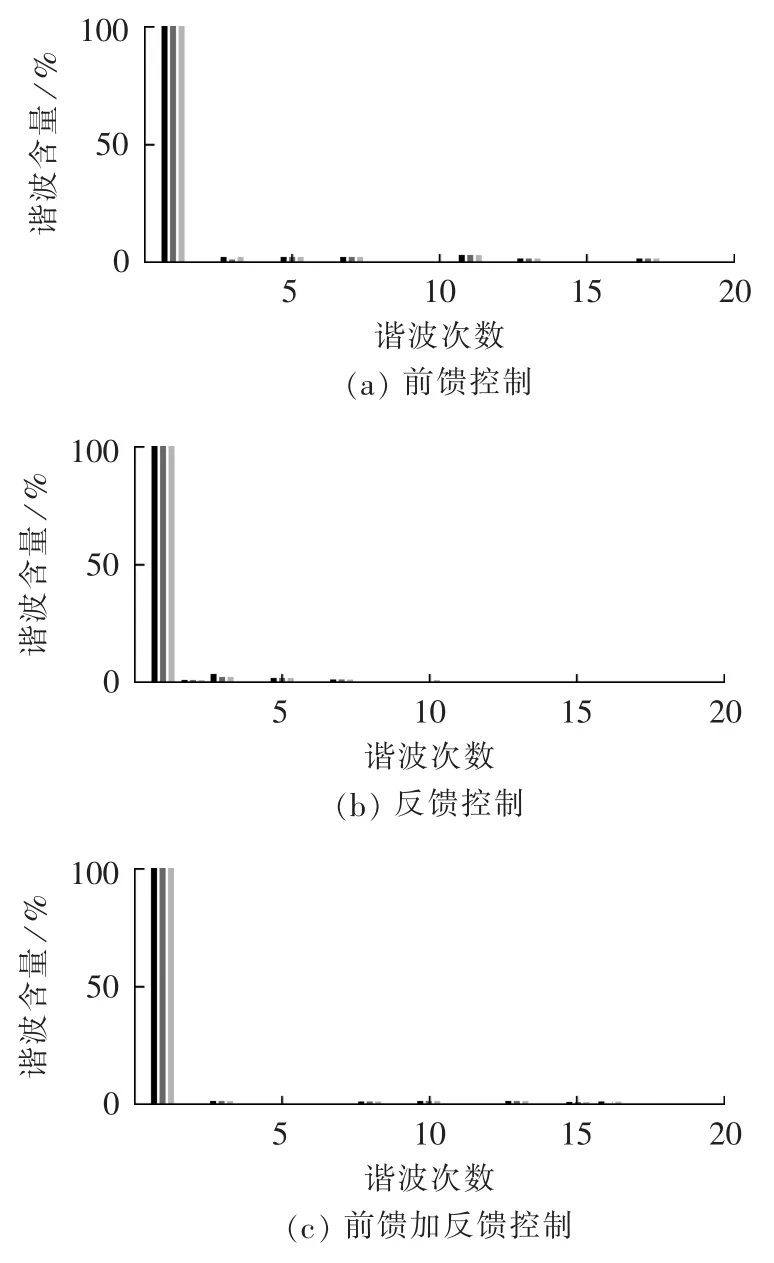
图12 谐波补偿后电源电流频谱图Fig.12 Spectrum of source current after harmonic compensation


图13 三相电源电流、中线电流及a相电源电压波形Fig.13 Waveforms of three-phase source current,neutral current and phase-a source voltage
5 结论
本文提出一种谐波电流检测法,可检测出三相四线制系统任意次谐波电流的正、负、零序分量及无功电流。本文还提出同时检测电源电流和负载电流的前馈加反馈的选择性补偿控制策略,其特点如下。
a.检测负载电流进行前馈控制;检测电源电流进行反馈控制,反馈控制采用基于多个同步旋转坐标系下的积分控制,可以对各次谐波分量及无功分量实现零稳态误差补偿。积分器承担积分调节和滤波的双重作用,避免了采用低通滤波器引起的延时和对系统稳定性的影响,同时简化了控制策略。
b.可以根据需要补偿指定次数的谐波,具有很强的针对性和实用性。
c.兼顾良好的补偿效果和动态性能,不仅可以补偿稳定的非线性负荷,还可以补偿快速变化的非线性负荷,具有较广阔的应用前景。
d.前馈加反馈的控制策略相对较复杂,这就对DSP的计算能力提出较高的要求。随着DSP芯片的发展,用新型高性能DSP或采用FPGA代替DSP实现该控制策略,将大幅提高该控制策略的实用性。
仿真和实验验证了该控制策略可以精确地补偿非线性负载产生的各次谐波、中线零序电流、三相不平衡分量及无功分量,并具有良好的动态性能。
