无传感器混合式LLC电路同步整流数字控制策略

刘和平，李金龙，苗轶如，彭东林

（1.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044；2.重庆理工大学 机械检测技术与装备教育部工程研究中心，重庆 400054）

0 引言

LLC谐振电路因具有变压器原边零电压开关（ZVS）和次级整流零电流开关（ZCS）的特性[1]，越来越多地用于高效率变换器电路中。谐振电路应用较多的控制方式可分为变频VF（Variable-Frequency）控制和移相PS（Phase-Shift）控制2种，2种控制方式的驱动信号占空比都为50%，以频率或相位差来调节输出电压。早期LLC电路的控制以变频控制为主，当输入电压和负载变化较大时，要求谐振主开关的开关频率变化范围大，对变压器等磁性器件的设计不利。特别是当LLC电路工作于连续模式时[2-4]，电路增益对频率的变化极不敏感，且效率会降低。为此，文献[5]采用定频控制，变频器低压工作于3L（即3电平）模式，高压时工作于2L模式，然而开关数目多，结构复杂。文献[6]提出一种新颖的混合式控制策略，使变换器具有变频和移相模式，适用于宽范围输入电压应用场合。

本文以谐振开关损耗最小为依据，对文献[6]所提出的混合式LLC电路进行了最优模式转换点确定的优化，并提出一种适用于混合式LLC电路的无需增加额外传感器的数字式同步整流控制策略。该策略通过判断输出电压的变化，以最优梯度滞环比较算法实现同步整流驱动最优占空比的搜索。

1 LLC电路混合式控制

图1所示是全桥LLC谐振变换器主电路。图中，VQ1—VQ4是谐振主开关；VSR1—VSR4是同步整流MOSFET；Cr是谐振电容；Lr是谐振电感，Lm是励磁电感，Lr、Lm以变压器的漏感和励磁电感实现。

图1 带同步整流的LLC电路Fig.1 LLC circuit with synchronous rectification

混合式控制分为变频模式和移相模式。变频模式的主要波形如图2（a）所示，在不同的主开关频率fs下，LLC电路的直流增益可表示为：

图2 理想驱动波形Fig.2 Ideal driving waveforms

其中，k为谐振电感与励磁电感比值；x为主开关频率fs与谐振频率fr比值；Q为电路品质因数。

根据式（1）可得到输入-输出电压增益曲线，如图3（a）所示（k=6）。从图中可以看出，变频工作模式下LLC电路输入电压变化大时，主开关频率fs的变化范围很宽，特别是在高频段，电路增益对频率变化极不敏感，这不利于控制和磁性器件的设计。

图3 全桥LLC电路输入-输出电压增益曲线Fig.3 Input-output voltage gain curve of full-bridge LLC circuit

为改善LLC电路频率变化大的缺点，文献[6]提出一种在高频时采用移相模式的控制策略，其主要波形如图2（b）所示，具体工作过程详见文献[6]，此处不再赘述。

移相模式下的增益表达式是关于电路参数的隐函数，由式（3）确定。

其中，带“*”的量是经标幺化处理的值。式中已知的参变量有：

其中，Ts为谐振周期。则电路增益M可表示为谐振主开关重合相位占空比Dy的隐函数，借助于数学分析软件Maple进行数值计算，可以得到不同品质因数Q条件下电路增益与Dy的关系曲线（k=6），如图3（b）所示。

从图3（b）可以看出，在移相工作模式下，保持频率不变，随着主开关相位的移动，电路增益可以从0变化到1，改善了变频控制模式下电路增益对高频段不敏感的缺点。2种控制模式的结合，可以使LLC电路在较小的频率变化范围内得到较大的电路增益，改善了LLC电路的设计和控制难度。

但文献[6]未对控制模式转换点如何确定进行分析，文中实验也只是将其确定在谐振频率附近，并未提供依据，本文将以开关损耗最小为依据对最优转换点进行分析，以确定最优转换点选取原则。

2 模式转换最优点的选择

开关电源的损耗可分为开通损耗、关断损耗和导通损耗3个部分。LLC电路主开关管是零电压开关，可忽略其开通损耗。

2.1 导通损耗

主开关管VQ1—VQ4的开关波形如图4（a）所示，图中UGS-Q1和UDS-Q1分别是VQ1驱动电压和漏源极压降，Ud1是VQ1寄生二极管压降，则导通损耗分为体二极管导通损耗和MOSFET导通损耗。

图4 主开关管导通与关断Fig.4 Turn-on and turn-off of main switch

a.体二极管导通损耗。

根据图4（a）所示的主开管导通过程，可以得到其导通时间和导通电流。在近似认为导通压降usd为0.7 V条件下，这个阶段的功率损耗可近似表示为：

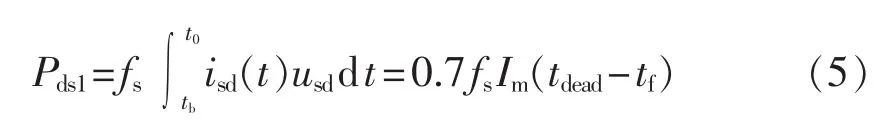
b.MOSFET导通损耗。

图4（a）中的t0～t3时间内为VQ1导通阶段，根据图2，在此时间段内的电流可分为t0～t2的谐振段和t2～t3的恒流段。

设VQ1的导通电阻为Ron，则导通损耗可以表示为：

将不同时间段的电流代入可得：

2.2 关断损耗

关断过程的电流和电压波形如图4（b）所示，在关断过程中，电流不会瞬间降为0，而是可以看作线性降低。所以，开关管VQ1的关断损耗可表示为：

在忽略零电压开关开通损耗的条件下，LLC电路单管总损耗可以表示为：

由式（9）可知，LLC电路单管总损耗与Im成正比。

由式（4）可得：

对上式求导可得：

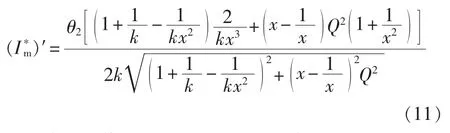
当x取值大于1时，因LLC电路次级整流不再是零电流开关关断，会增加额外的损耗，因此，混合控制模式转换频率应小于谐振频率fr，即x≤1。

由式（11）可知，在 0＜x≤1 范围内（I*m）′小于 0，说明I*m呈递减趋势，因此选择x=1，即fs=fr时Im值最小，主开关管损耗最小，LLC谐振变换器效率最高。

3 混合控制的LLC同步整流数字控制策略

LLC电路因其所具有的优良软开关特性，在越来越多的场合得到应用。但在一些低压输出应用中，若次级整流采用普通二极管整流会造成很大的整流损耗。为提高LLC电路在低压大电流输出时的效率，同步整流被应用到LLC电路[7-16]。图1为全桥同步整流LLC谐振变换器主电路。同步整流以导通电阻仅几毫欧的MOSFET管代替二极管进行整流，可极大地减小整流损耗，提高变换器效率。

从图2中可以看出混合式控制LLC电路的次级整流电流为谐振断续，这决定了一般的同步整流方案不能适用，例如电压型自驱动、变压器多绕组驱动等。而普遍适用的电流检测型又需增加额外的电流检测器或电流互感器，增加了电路的复杂度，且容易受电路电感等寄生参数的影响。

本文基于LLC电路输出电压与次级同步整流驱动占空比DSR关系提出一种无传感器同步整流控制策略。

3.1 同步整流控制策略反馈量

对于整流电流断续，同步整流驱动可分为以下3种情况。

a.整流驱动时间 Ton_SR（Ton_SR=DSRTs）等于电流持续时间，整流管的驱动信号与整流电流完全同步，无整流MOSFET体二极管导通损耗。这种情况整流损耗最小，整流管压降最低，输出电压达到最大值。

b.Ton_SR小于电流持续时间，则在驱动信号消失后整流电流将从整流MOSFET转移到体二极管，整流管的压降Ud为二极管导通压降（约0.7 V），这个压降远大于有驱动信号时MOSFET的导通压降。

在几十安电流流过导通电阻为几毫欧的MOSFET时产生的压降小于0.1 V，可近似认为：

这个压降变化经电容滤波后，表现为电路输出电压的下降。

c.Ton_SR大于电流持续时间，将形成环流，电流反向流动，电能从滤波电容反向传输到输入电源，造成输出电压的快速下降。

图5是图1所示LLC电路保持主开关频率fs不变、初始输出电压3.3 V条件下，实测的同步整流驱动占空比DSR与输出Uout关系。

图5 DSR与输出Uout的关系Fig.5 DSRvs.Uout

如图5所示，当Ton_SR向最优驱动点改变时输出电压变化ΔUo为正，向相反方向改变时ΔUo为负。因此，同步整流管驱动优劣的变化会造成输出电压高低变化，可以将其作为同步整流驱动占空比调节的反馈量，它已经在LLC电路谐振控制中检测得到，因此无需额外传感器。系统总的控制原理图见图6。

图6 无传感器同步整流系统控制框图Fig.6 Block diagram of sensorless synchronous rectification control

3.2 同步整流最优梯度滞环比较寻优的算法实现

LLC混合电路的最优同步整流驱动波形如图2所示，当有整流电流时开通整流MOSFET，在电流过零时关断。

从图2中可以看出，无论是在变频或移相模式，整流电流的开通时刻总是和主开关中滞后管相同，而关断根据电流的不同而不同。结合图5，同步驱动占空比的调制可用最优搜索方法实现。综合比较目前较为常用的搜索法，滞环比较法较适合于本文控制。

采用滞环比较搜索最优同步驱动占空比时，选取3 个间隔 dstep的驱动占空比（DSRA、DSRB、DSRC），得到它们分别对应的输出电压（UoutA、UoutB、UoutC），比较相邻两电压的大小，每组结果有大于、相等和小于3种情况，且2组的结果相互独立，因此会共有9种可能。定义 UoutC＞UoutB、UoutB＞UoutA为“+”，等于记为“0”，小于记为“-”，可得图7的9种关系。

图7 3点之间电压比较可能出现的关系示意Fig.7 Possible relations of voltage comparison among three points

根据图5和图7，同步驱动占空比调制过程如图8 所示，图中（A）、（B）、（C）是当前步 DSR点，A、B、C是下步DSR点。如果2次比较结果之和为“+”，则下一时刻 DSR=DSRC+dstep，去掉（A）点，并对（B）、（C）点及新DSR点重新编号A、B、C；反之如果2次的比较结果之和为“-”，则 DSR=DSRA-dstep，去掉（C）点，并对新DSR点及（A）、（B）点重新编号 A、B、C；当 2 次比较结果之和为“0”时，取中间点即可得到最优DSR，对其编号 A、B、C，停止搜索。

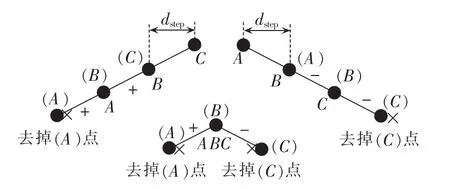
图8 滞环比较调节示意图Fig.8 Schematic diagram of hysteresis comparison adjustment

滞环比较方法搜索的快慢与步长dstep有关，dstep较小时搜索速度慢；dstep较大时搜索速度快，但可能存在较大的稳态误差。本文针对此缺点对滞环比较法进行了优化改进，得到新的最优梯度滞环比较法。

最优搜索法的数字实现时，一般以差分近似代替微分，图5中的2点梯度可近似用2点电压差表示，因此DSR的搜索步长可表示为：

其中，α是非负常数。根据图5和式（13），在远离最优DSR点时2点间的电压差大，搜索步长大，搜索速度快；接近最优点时，电压差小，搜索步长会越来越小并趋于0，并最终稳定在最优点，A、B、C 3点重合。当负载、输入电压等条件变化引起输出电压变化时，式（13）不再等于0，将会自动起动搜索过程，重新搜索到最优DSR点。

根据以上分析，同步整流驱动的系统控制流程如图9所示。通过数字控制器（ADC）模块将输出电压Uout检测值根据dstep的正值不同分别赋予UoutA或UoutC，以式（13）计算新的 dstep值，并以它的正负来选取新的同步驱动占空比和新的A、B、C点，最后将新的占空比值和谐振控制的周期送入数字控制器的PWM模块，产生同步整流驱动PWM信号。

图9 同步整流驱动的数字式系统控制流程Fig.9 Flowchart of digital system control driven by synchronous rectification

本文所提出的改进型最优梯度滞环比较算法可以以较快的速度搜索到最优点，并稳定在最优点消除稳态误差和振荡，还可以在最优点变化时自动启动最优搜索，动态调节性能好。

实验表明同步整流驱动控制与混合式LLC谐振数字控制之间无明显的制约关系，在2个子程序中分别执行，可根据实际情况选择两者不同的调节速度，若在同步整流要求严格的情况下应使同步整流控制调节速度快；若要求整个动态性好应使谐振控制调节速度快。

4 实验验证

为验证本文所提出的同步整流控制策略的正确性和可行性，进行了实验样机的验证。

本文搭建了输入36～72 V、额定输入电压60 V、输出3.3 V／20 A、主开关频率范围60～100 kHz、谐振频率fr和模式转换频率ft为100 kHz的LLC实验样机进行实验验证，其中整流MOSFET是导通电阻4.2 mΩ英飞凌公司的IPB042N10N3G，数字控制器为TI公司的TMS320F2808，MOSFET驱动芯片为ST公司的L6375，实验实测波形如图10—14所示。

图10是同步整流MOSFET漏源极电压UDS和其驱动信号UGS波形，图10（a）是同步驱动未达到最优驱动波形，图10（b）是同步驱动达到最优驱动波形。从图中可以看出，同步整流管漏源极导通压降在有驱动和没驱动有较大的电压差（约0.6 V）。

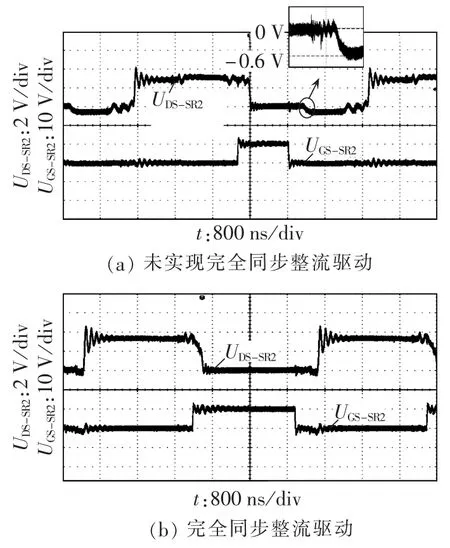
图10 整流MOSFET UDS和UGS波形Fig.10 UDSand UGSwaveforms of rectification MOSFET

图11（a）是为额定输入电压60 V、满负载条件下（fs=100 kHz），谐振电流 ir、整流电流 iSR和主开关驱动波形；图11（b）是整流管漏源极电压UDS和同步驱动UGS波形，展示了几者间的相位关系。

图12（a）、（b）分别为输入电压为 36 V、满负载和轻载（20%满载）时的整流电流iSR、整流管漏源极电压UDS和其驱动信号UGS波形，验证了变频模式下同步整流控制的正确性。

图11 额定条件下实验波形（fs=100 kHz）Fig.11 Experimental waveforms under rated conditions（fs=100 kHz）

图12 36 V输入实验波形Fig.12 Experimental waveforms with 36 V input

图13（a）、（b）分别为输入电压为 72 V、满负载和轻载（20%满载）时的整流电流iSR、整流管漏源极电压UDS和其驱动信号UGS波形，验证了移相模式下同步整流控制的正确性。

图14是fs=100 kHz、Dy=0.8时的整流电流iSR、整流管驱动信号UGS和移相主开关驱动波形，得到接近于图2所示的理想驱动波形。

图15从上至下是输入电压从72 V变到36 V时的输出电压Uout、整流电流iSR和整流管驱动UGS-SR2、UGS-SR4波形。左边的放大图是变化前谐振处于移相模式，右边的放大图是变化后谐振处于变频模式。从图中可以看出，LLC变换器能稳定输出电压，在动态变化前后同步整流驱动都与整流电流有较好的同步关系，验证了本文方法有较好的动态调节性能。

图13 72 V输入实验波形Fig.13 Experimental waveforms with 72 V input

图14 Dy=0.8时移相实验波形Fig.14 Experimental waveforms of phase-shift when Dyis 0.8

图15 输入电压72 V变36 V动态响应Fig.15 Dynamic response to input change from 72 V to 36 V

从以上的实验波形可以看出，在不同的输入、不同负载和动态条件下，整流管漏源极间的压降都不会出现较大的体二极管导通压降（如图10（a）所示），说明控制策略能很好地调制同步整流驱动占空比使其与整流电流保持同步，有较好的同步整流效果，与前文分析相吻合，策略能满足实现应用要求。

图16是输入电压为36 V和72 V、模式转换点设置在85 kHz和100 kHz时，变换器效率与输出电流的关系，证明了转换频率设定低时会造成效率降低。

图16 效率与负载关系Fig.16 Relationship between efficiency and load

5 结论

本文详细分析了混合式LLC电路的开关管损耗，以开关损耗最低确定了模式最优转换点。基于输出电压与同步整流驱动的关系，提出一种适用于混合式LLC电路的无传感器同步整流自调整控制策略。以一个36～72 V输入、3.3 V／20 A输出的实验样机验证了本文控制策略在不同输入、不同负载和动态条件下的正确性与可行性。本文同步整流控制策略具有以下优点：不需增加额外的传感器；改进的滞环比较搜索法能快速准确搜索到最优同步驱动；具有较好的动态调节性能；LLC电路在不同工作模式下都有良好的同步驱动效果。