关于Boussinesq系统行波解的探求①

杜海清（江苏淮阴师范学院数学系，江苏 淮安 223300）

关于Boussinesq系统行波解的探求①

杜海清
（江苏淮阴师范学院数学系，江苏 淮安 223300）

主要考虑利用三角函数方法，双曲正切函数方法，双曲正割函数方法和Jacobi椭圆函数方法去获得Boussinesq系统的精确行波解.

Boussinesq系统；Jacobi椭圆函数；行波解

0　引言

近来，对非线性演化方程的直接求解方法受到越来越多的重视，一些用来获得非线性演化方程精确行波解的方法被发展起来.基本思想如下：对于含有两个变量的非线性演化方程

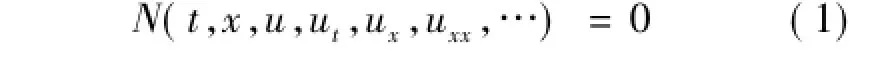
考虑形如

的精确解（其中c为常数）.不失一般性，设k＞0.将（2）代入（1）得到关于u（ζ）的一个常微分方程，然后将u（ζ）展成f（ζ）的多项式

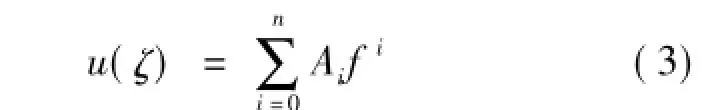
其中Ai是待定常数，最高阶数n由方程（1）确定.现对一类不同时含有偶数阶和奇数阶偏微商项的非线性演化方程进行讨论，从而获得一些精确行波解，但（3）中的f（ζ）满足第一种椭圆方程［1］.

其中p，q和r是常数，这样方程（3）就建立了方程（4）的解与（1）的解之间的一种代数映射关系.本文将上述方法应用于Boussinesq系统［2］

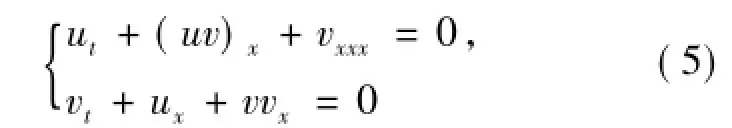
并得到一些新的精确解.

将（2）代入方程组（5）可得

积分一次有

其中c1，c2是积分常数.

从（7）的第二个方程中解出u并代入第一个方程得

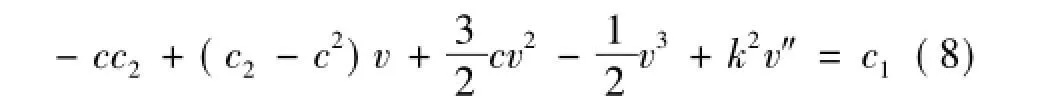
将方程v（ζ）=A0+A1f（ζ）（A0，A1为待定常数）代入方程（8）并利用方程（4）得

比较f的各次幂，有

由此可得

于是Boussinesq系统有下列形式的精确解

下面将讨论方程（4）中f的特解

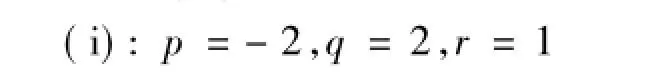
方程（4）有解f（ζ）=tanh（ζ），则Boussinesq系统有精确解

（ii）：p=-（1+m2），q=2m2，r=1

方程（4）有解f（ζ）=snζ于是Boussinesq系统有周期性的孤子波解

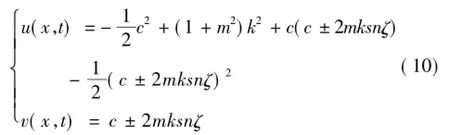
当m→1时，snζ→tanhζ，则从（10）得到（9）. （iii）：p=2-m2，q=2，r=m'2≡1-m2

当m→0时，snζ→sinζ，cnζ→cosζ，dnζ→1则由方程（11）可得方程（5）的三角函数波解

当m→1，方程（11）退化为

（iv）：p=-（1+m2），q=2，r=m2

和

当m→0时，方程（12）和（13）退化为

和

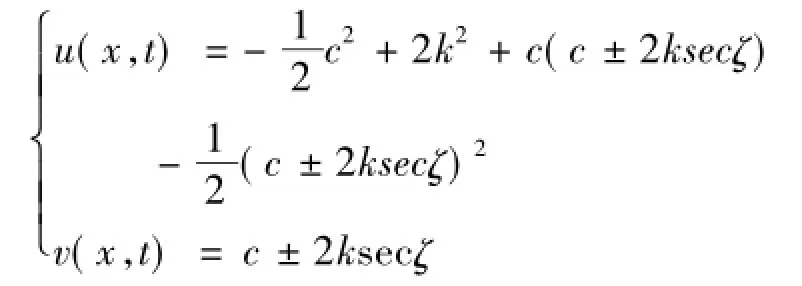
当m→1时，由方程（12）得

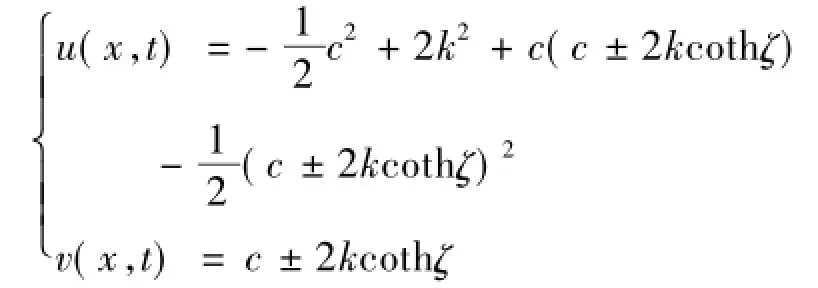
而方程（13）退化为一个常数解

［1］Y Z Peng.A Mapping Method for Obtaining Exact travelling Wave Solutions Tononlinear Evolution Equations（to appear）.

［2］Kaup D J.A Higher-order Water-wave Equation and the Method for Solving it［J］.Prog Theo Phys，1975，54（7）：396-408.

Discussion on Traveling Wave Solutions of Boussinesq System

Du Hai-qing

（Dept of Math，Huaiyin Teachers＇coll，Huaian，223300，China）

In this paper，triangle function methods，hyperbolic function methods and Jacobi elliptic function methods were used to obtain exact traveling wave solutions of a Boussinesq system.

Boussinesq system；Jacobi elliptic function；traveling wave solution

中图文分类号：O175.4A

1008-1402（2015）06-0830-02

2015-10-21

杜海清（1966-），男，江苏涟水人，副教授，硕士，主要从事数学教育和可积系统研究..