含u'的二阶非线性完全边值问题①
2015-09-18孙文斐张建军郑州城市职业学院河南郑州452370
孙文斐, 张建军(郑州城市职业学院,河南 郑州 452370)
含u'的二阶非线性完全边值问题①
孙文斐, 张建军
(郑州城市职业学院,河南 郑州 452370)
基于边值问题的上下解,利用单调迭代方法,对二阶非线性完全边值问题含的情况进行讨论,得出了二阶非线性完全边值问题的解的存在性.
上下解;单调迭代方;全连续算子;Arzela-Ascoli定理
0 引言
非线性泛函分析是现代数学有广泛引用价值的研究方向.它的研究成果广泛应用于各种非线性微分方程、积分方程和其他各种类型的方程以及计算数学、最优化理论、控制理论、动力系统、经济数学等许多领域.
边值问题是目前分析数学中最为活跃的领域之一.其中n阶边值问题,许多科学家用非线性泛函分析中的拓扑度理论、临界点理论、半序方法、上下解方法、不动点理论、迭合度理论、单调迭代方法等理论和方法,对此问题进行了深入研究.
本文考虑中含的二阶非线性完全边值问题

利用上下解方法同时假f定关于常数M>0,N >0满足条件
1 二阶非线性完全边值问题

其中f(t,u(t),u'(t)):[0,1]×R×R→R为连续函数.
定义1若α(t)∈C2[0,1],满足

则称其为边值问题(3)~(4)的下解.若上式中的不等号取反向,则称α(t)为(3)~(4)的上解.
引理1设u∈C2(I),N,M为常数N>0,M <0,且N2+4M>0

定义2在α≤β,α'≤β'的情况下讨论单调迭代方法.关于函数f(t,u,x)作如下假设(H),
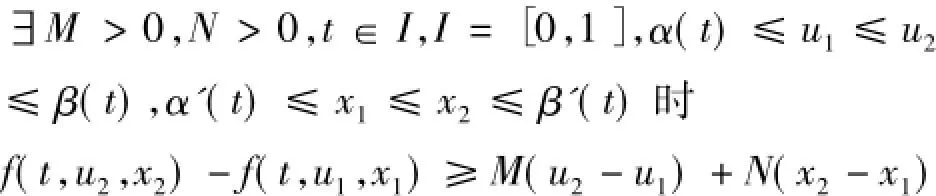
定理: 若二阶边值问题(3)~(4)存在下解α及上解β满足连续,满足假设(H),则分别u0=α,β以为初始项用线性迭代方程

做迭代序列αn及βn有

证明: 对∀η∈C'(I)考虑线性边值问题
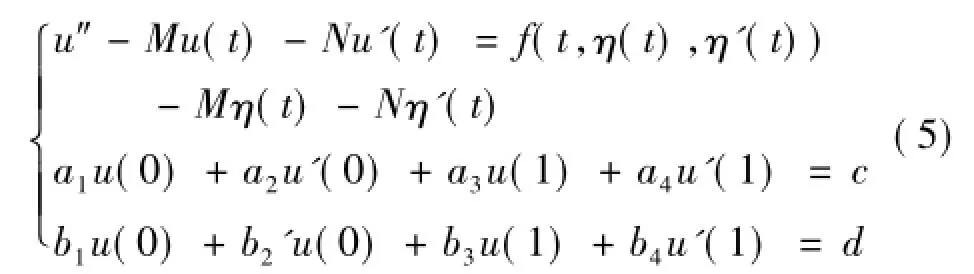
由引理1知,方程(5)存在唯一解,记为u=
Qη,那么

其中c11(0),c21(0)是由方程组(5)解得的常数.下面可证Q:C'(O)→C'(I)为全连续算子,要证Q:C'(I)→C'(I)为全连续算子只需证是Q紧的,并且Q是连续算子.
先证Q是紧的,即需证当S是C'(I)有界集,Q(S)是列紧的,由Arzela-Ascoli定理知之需证Q(S)一致有界且Q'(S)等度连续.
证明: 先来证Q(S)一致有界.由Qη(t)的表达式可得

那么由f(t,η(t),η'(t)),η(t),η'(t)在[0,1]上连续和 Qη(t),(Qη)'(t)表达式易得 Qη(t),(Qη)'(t)在[0,1]上一致有界,所以Q(S)中诸函数一致有界.
Q'(S)的等度连续性可以由(Qη)'(t)的表达式容易得证.
总上所述Q:C'(I)→C'(I)为全连续算子,易见u为边值问题(3)~(4)的解的充要条件是:u 为Q的不动点.令

则α,β∈D易见D为C'(I)中的有界非空凸闭集,下分3部分完成定理证明.
(1)证明Q(D)⊂D
任取η∈D,令u=Qη,由Q,α,D的定义及(H)有

由引理1知u(t)≥α(t),u'(t)≥α'(t),用β -u代替u-α可得:u≤β,u'≤β',因此u∈D,于是Q(D)⊂D.
按Q的定义及假设(H)有
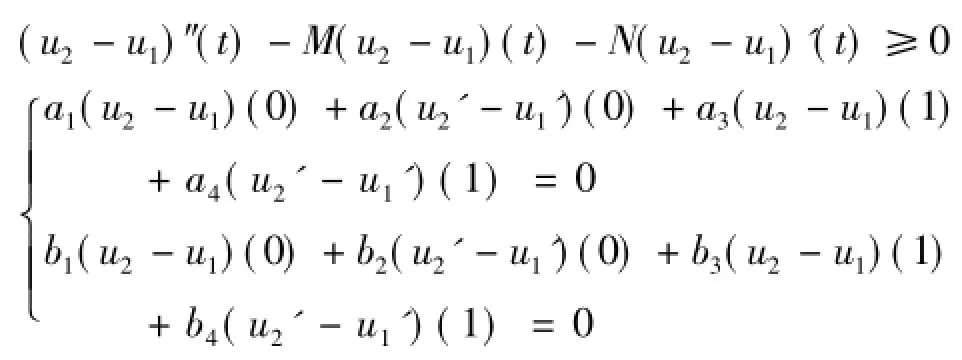
由引理3知u2≥u1,u2'≥u1'.
(3)取α0=α,β0=β,做迭代序列

按Q的定义{αn},{βn}为按线性迭代方程(5)所做的序列,按证明(1),(2)有

令n→∞,有

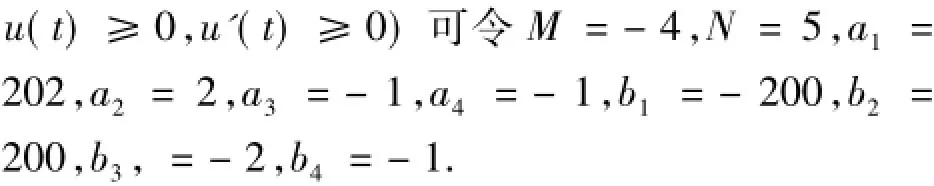
[1]郭大钧,孙经先.抽象空间常微分方程[M].济南:山东科学技术出版社,2002.
[2]郭大钧.非线性泛函分析[M].济南:山东科学技术出版社,2001.
[3]张恭庆,林源渠.北京:北京大学出版社,2010.
[4]Cabada A.The Method of Lower and Upper Solutions for Second,Third,Fourth and Higher Order Boundary Value Problems JMath AnalAppl,1994,185:302-320.
With u'of Second-order Nonlinear BoundaryValue Problem Completely
SUN Wen-fei, ZHANG Jian-jun
(City University of Zhengzhou,Henan zhengzhou,452370,China)
In this paper,based on the boundary value problem of upper and lower solutions,using the monotone iterative method,the second order nonlinear complete boundary value problem with was discussed,and the existence of the solution for the second order nonlinear complete boundary value problem was obtained.
Monotone interative;Upper and lower solutions;Complete continuous;Arzela-Ascoli theorem
O177.91
A
1008-1402(2015)06-0804-03
2015-09-22
孙文斐(1986-),男,河南郑州人,郑州城市职业学院硕士研究生.
