物资配输问题探讨及Matlab求解①

田富国（泉州经贸职业技术学院，福建 泉州 362411）

物资配输问题探讨及Matlab求解①

田富国
（泉州经贸职业技术学院，福建 泉州 362411）

对物资配输问题存在的产销平衡和产销不平衡两种情况进行探讨，并建立线性规划模型，利用Matlab提供的线性规划函数linprog对问题进行求解.

物资配输；数学模型；线性规划；Matlab

0　引言

在国民经济建设中，会遇到物资的配输问题，如煤炭、石油、钢材、水泥、食品等物资的配输，在全国有多个生产基地，要将这些物资配输到各消费地点，在现有交通条件下，如何选择一个合理的配输方案实现总运费最少.

物资的配输问题存在两种情况：产销平衡和产销不平衡，对于产销不平衡问题可以转化为产销平衡问题来进行求解［1～2］.

1　产销平衡问题

首先举一典例来阐述产销平衡问题：

某石油公司有三个产地P1，P2，P3，要运输到M1，M2，M3，M4，M5五个销售点，产地P1的石油日产量为200t，产地P2的石油日产量为500t，产地P3的石油日产量为300t，M1，M2，M3，M4，M5五个销售点的日需求量分别为200t，250t，150t，350t，50t，各产地到各销售点单位运价如表1所示，设计一个合理的配输方案使得运输总费用最小.

表11　单位运价表（单位：元/t）

产地的石油日产量和销售点的日需求量相等，这是一典型的产销平衡问题.这是一种理想的情况，实际情况往往不是这样，但为了研究问题方便，我们可以先作这样的假设.

这是一个线性规划问题，首先构建数学模型.

假设产地P1，P2，P3向销地M1，M2，M3，M4，M5配送的运输量分别是X1，X2，……X15，设最小运费为Smin，则

约束条件如下：

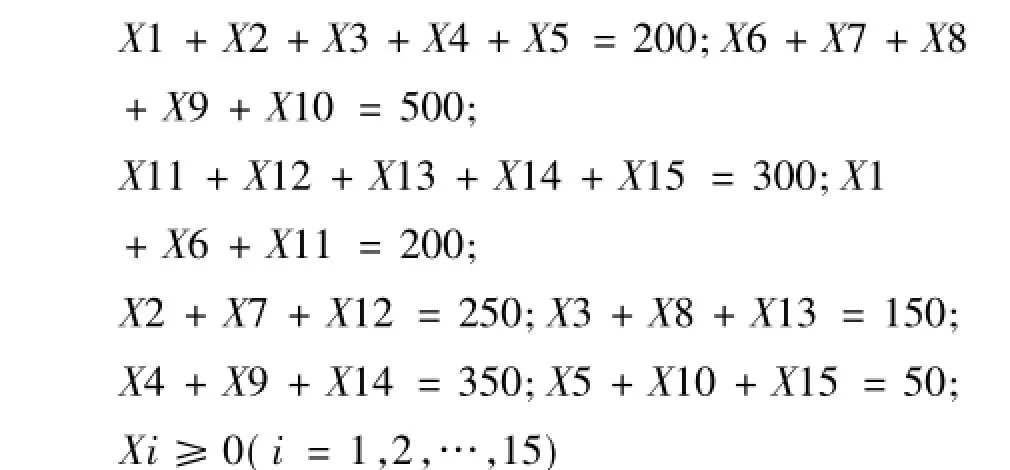
软件Matlab提供的线性规划函数linprog［3～4］，可以对问题进行求解.下面用Matlab编程求解该问题：

运行后的结果为：

对以上运算结果配送的吨位进行取整，可设计该问题的最优配送方案如表2所示：

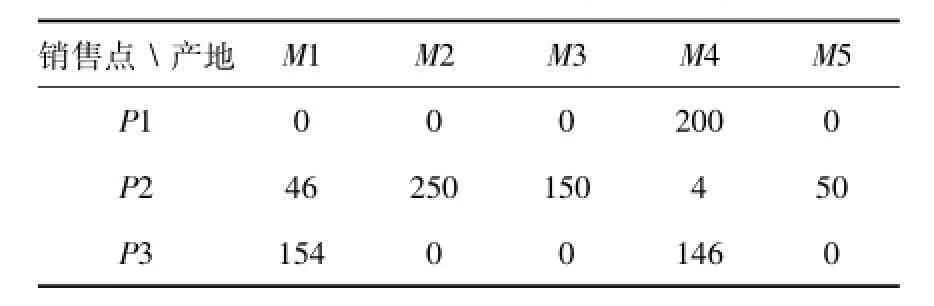
表2　最优配送方案（单位：t）

实现最优配送方案，所需最小总费用为：

Smin=200×13+46×20+250×17+150×11

+4×18+50×17+154×18+146×16=15450（元）

2　产销不平衡问题

产销不平衡问题存在两种情况：产地产量大于销售点需求量和销售点需求量大于产地产量.对于产销不平衡问题，转化为产销平衡问题来进行求解.下面分两种情况进行讨论：

2.1产地产量大于销售点需求量

若将上述典例的产地P1，P2、P3的石油日产量改为400t，700t，300t，则是属于产地产量大于销售点需求量这种情况.这时，我们可以虚设一个销售点M0，让多余的产量都运抵此虚设的销售点，并令从各产地运抵销售点M0的单位运价均为0.则单位运价表和产销平衡表如表3和表4所示：

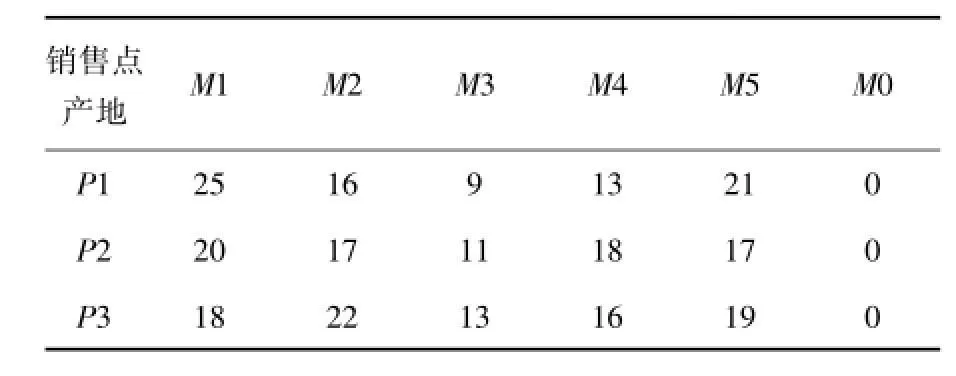
表3　单位运价表（单位：元/t）

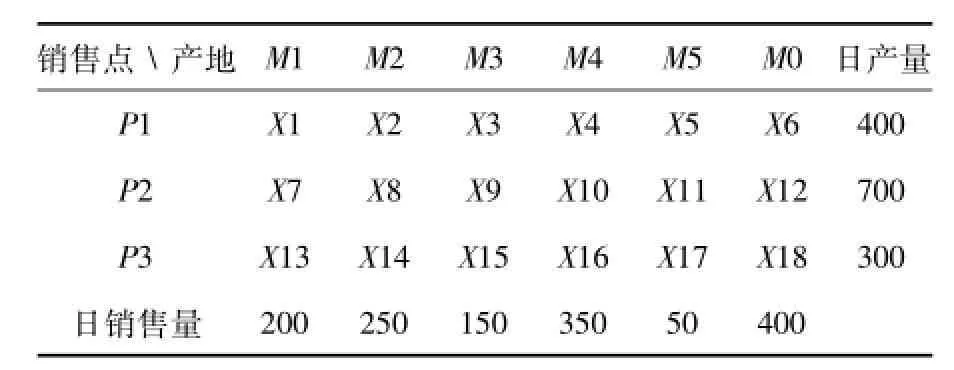
表4　产销平衡表（单位：t）

则构建数学模型如下：

下面用Matlab编程求解该问题：

运行后的结果为：

根据以上运算结果，设计该问题的最优配送方案如表5所示：

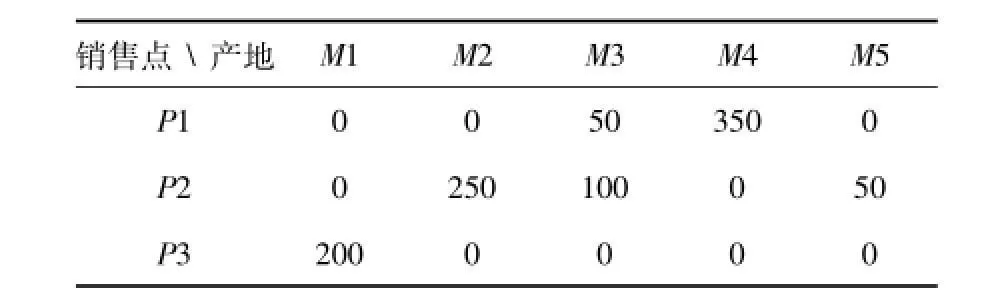
表5　最优配送方案（单位：t）

实现最优配送方案，所需最小总费用为：Smin=50×9+350×13+250×17+100×11

+50×17+200×18=14800元

2.2销售点需求量大于产地产量

若将典例的其他条件不变，销售点M1，M2，M3，M4，M5的石油日销售量改为300t，250t，350t，250t，150t，则该问题是属于销售点需求量大于产地产量这种情况.这时，我们可以虚设一个产地P0，并令此虚设的产地P0运往各销售点的单位运价均为0.则单位运价表和产销平衡表如表6和表7所示：

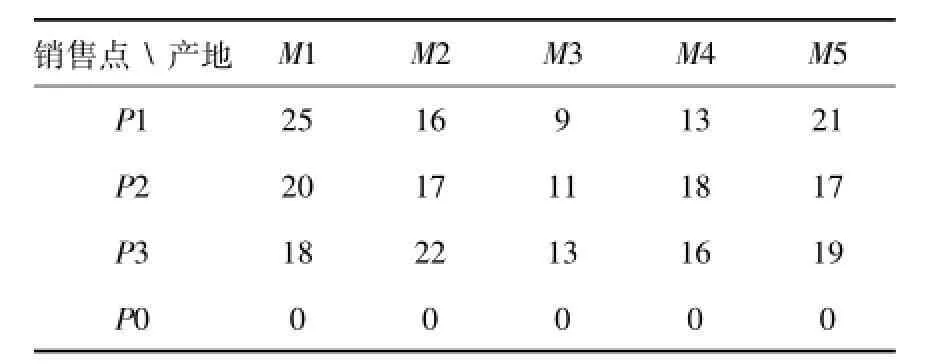
表6　单位运价表（单位：元/t）

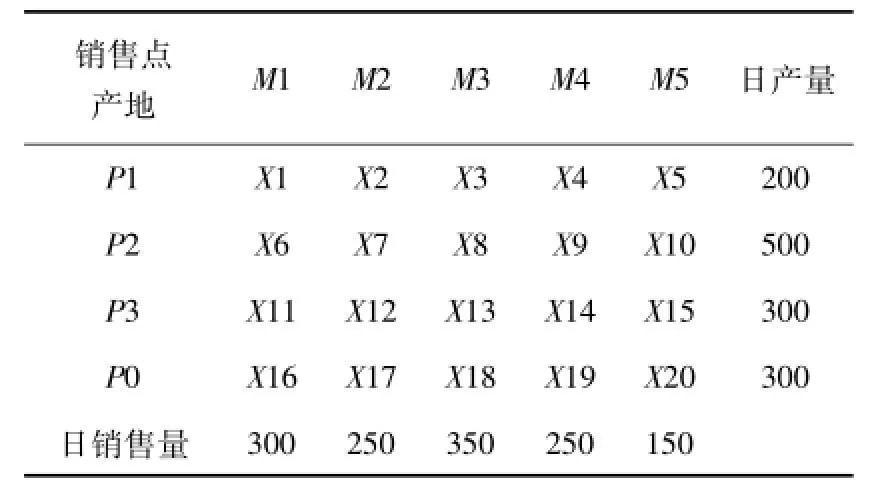
表7　产销平衡表（单位：t）

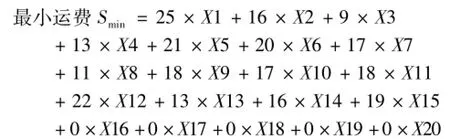
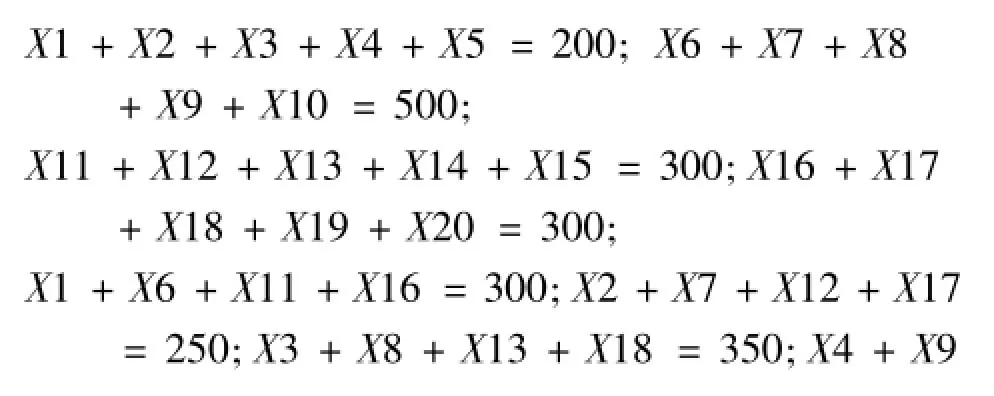
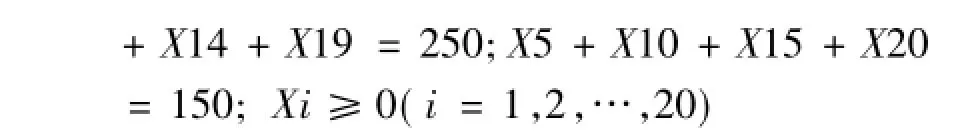
构建数学模型如下：约束条件如下：下面用Matlab编程求解该问题：

运行后的结果为：

对以上运算结果配送的吨位进行取整，设计该问题的最优配送方案如表8所示：

表8　最优配送方案（单位：t）

实现最优配送方案，所需最小总费用为：

3　结语

物资的配输问题是一个线性规划问题.解决物资的配输问题，首先根据问题的具体条件建立线性规划的数学模型，写出目标函数和约束条件，然后利用软件Matlab提供的线性规划函数linprog对问题进行求解.

［1］ 胡运权，郭耀煌.运筹学教程（第二版）［M］.北京：清华大学出版社，2000.7.

［2］韩伯棠.管理运筹学［M］.北京：高等教育出版社，2003.5.

［3］黄雍检，赖明勇.MATLAB语言在运筹学中的应用［M］.长沙：湖南大学出版社，2005.5.

［4］ 陈杰.MATLAB宝典［M］.北京：电子工业出版社，2011.5.

Research on the Problem of Material Distribution and Solving the Problem with MATLAB

TIAN Fu-guo

（Quanzhou Vocational College of Economics and Business，Quanzhou，Fujian 362411，China）

The problem of material distribution was researched in this paper.The two kinds of situations：the balance of production and marketing，and the imbalance of production and marketing were discussed.Then，the linear programming model was set up and solved using the linear programming function LINPROG in Matlab.

material distribution；mathematical model；linear programming；Matlab

F224.31

A

1008-1402（2015）06-0810-03

2015-09-15

田富国（1974-），男，福建三明人，福建省泉州经贸学院讲师，厦门大学工程硕士，研究方向为控制工程.