基于Goertzel滤波器的两相静止坐标系下的增强型锁相环
2015-09-17吴凤江
李 伟,吴凤江,孙 力
(1.哈尔滨工业大学 电气工程系,黑龙江 哈尔滨 150001;2.黑龙江科技大学 电气工程系,黑龙江 哈尔滨 150027)
0 引言
在可再生能源并网发电系统、有源滤波器以及无功补偿系统等并网型电力电子系统中,为实现高性能并网运行,普遍采用锁相环技术来获得电网的实时同步信息,如电网电压的幅值、相角、频率等[1-6]。在上述系统中,除了锁相环算法以外,还要执行电流闭环控制、电压闭环控制、谐波检测以及脉宽调制等算法。因此,要求锁相环算法尽量简化,以减少对控制芯片资源的占用,更好地和上述算法相融合。
目前,在应用于三相系统的锁相环算法中,具有代表性的是基于同步旋转坐标系的锁相环以及基于三相静止坐标系的增强型锁相环,二者均能够准确地估计三相输入信号的同步信息并由此获得了广泛应用。其中,前一种方案利用同步旋转坐标变换将三相静止坐标系下的输入信号变换到两相同步旋转坐标系下的直流量,再通过对直流量的闭环控制实现相角和频率的跟踪[7-14]。所使用的旋转坐标变换中需要进行6次三角函数计算和乘法运算,计算稍显复杂。增强型锁相环在经典锁相环算法的基础上,加入幅值闭环估计环节,一方面可以获得电网电压的幅值信息,同时能够加快频率环的响应速度[15-16]。增强型锁相环对三相电网电压直接锁相,省去了旋转坐标变换环节,但是由于其是在三相静止坐标系下进行的,需要计算较多的三角函数运算和乘法运算,计算同样比较复杂。
另外,在实际系统中,还要考虑非理想电网条件,如谐波以及相间不平衡等对锁相环性能的影响。现有文献已经指出,谐波和相间不平衡将直接导致所估计的信息中产生周期扰动,严重影响锁相环的性能进而导致整个系统的性能恶化。由于经典锁相环算法并不能消除谐波和相间不平衡的影响,因此目前在锁相环的研究方面普遍围绕着如何改善非理想输入条件下锁相环的性能来开展,如在基于旋转坐标系下的锁相环中加入滤波器或者采用正负序分离技术再结合滤波器来同时消除不平衡和谐波的影响。而在增强型锁相环中同样需要加入滤波器来消除这一影响。
对于锁相环算法而言,最基本的要求是能够在三相输入信号存在谐波和不平衡时仍然准确估计三相输入信号的幅值、相角和频率信息,同时要求其具有较快的动态响应性能,以便在输入信号发生动态变化时能够尽快获得准确的信息以保持系统的高性能。另外,还要考虑整个锁相环算法,尤其是加入针对谐波和不平衡的性能优化算法以后的计算量问题。在前述列出的电力电子电能变换系统中,随着对整个系统性能的要求日益提高,系统的算法越发复杂,为其实现带来较大难度。而纵观目前的锁相环算法,普遍存在算法复杂、占用控制芯片资源过多等问题,虽然能够通过采取多处理器协同工作的方案来间接解决算法的执行问题,但是会带来开发周期长、调试难度大、成本增加以及可靠性下降等一系列负面问题。因此如何在实现优良估计性能的同时,尽量降低锁相环算法自身的复杂度,从而提高整个系统的集成度和执行效率,成为锁相环研究中新的热点和难点问题。
本文首次提出两相静止坐标系下的增强型锁相环 TPSF-EPLL(Two-Phase Stationary Frame Enhanced Phase Locked Loop),并给出了其详细的系统结构。所提出的锁相环算法在两相静止坐标系下进行运算即可同时获得输入信号的幅值、频率和相角信息,无需旋转坐标变换,从而使计算量大幅简化。而利用Goertzel滤波器能够对多个低次谐波同时滤除的特点,在每个闭环控制环节中只需要增加1个Goertzel滤波器即可同时消除三相电网电压不平衡和谐波对锁相环输出性能的影响。由于Goertzel滤波器基于滑动平均的思想,在实现过程中只需执行移位存储、加法和除法运算,因此不会明显增加算法的执行时间。
1 所提出的TPSF-EPLL
下面首先分析所提出的TPSF-EPLL的算法结构。假设三相电网电压为:
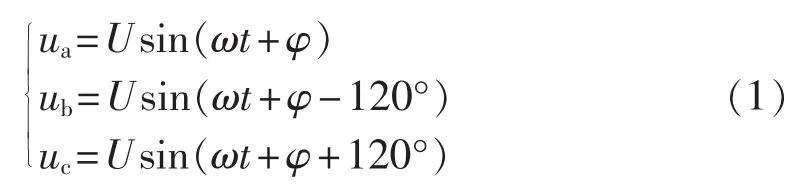
经过静止坐标变换,坐标变换公式为:

变为两相静止坐标系下的分量:

为了实现在两相静止坐标系下获得电网电压的幅值、相角和频率信息,需要确定所提出的TPSF-EPLL的结构。设锁相环所获得的两相静止坐标系下的瞬时信号的输出为:

其中,“~”代表由锁相环算法获得的各个变量的估计值。定义成本函数为输入信号与所获得信号差的平方和,即:
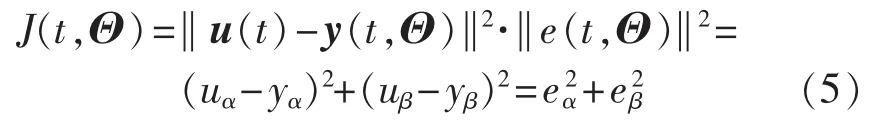
根据梯度下降法,可以得到迭代方程为:
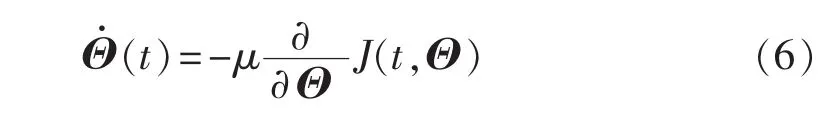
因此,展开式(6),可得:
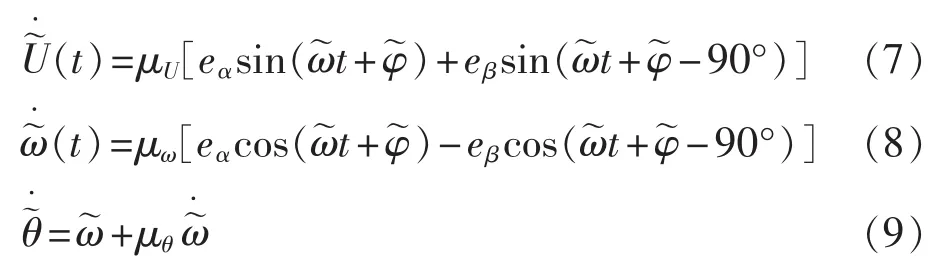
其中,μU为幅值环的积分系数;μω、μθ分别为频率环的比例和积分系数。
由以上分析可以获得所提出的锁相环的结构如图1所示。其中,实线表示向量运算,虚线表示代数运算。频率环增加了比例环节,以便提高系统的响应速度,其输出经过积分器后即获得输入信号的相角,由此得到了输入信号的幅值、频率和相角信息。

图1 所提出的TPSF-EPLL示意图Fig.1 Schematic diagram of proposed TPSF-EPLL
下面对所提出的TPSF-EPLL的稳定性进行分析进而获得参数设计原则。
将式(1)、式(2)代入式(7)—(9),得到:
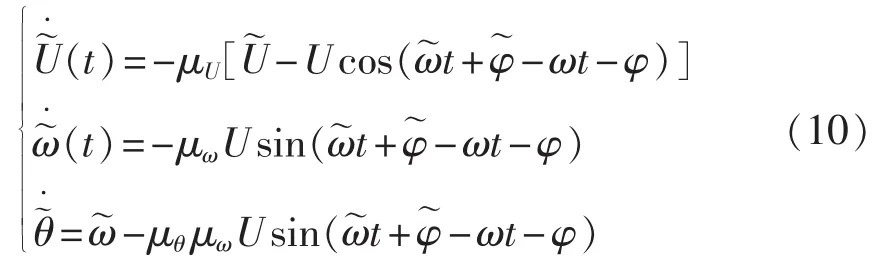
定义:
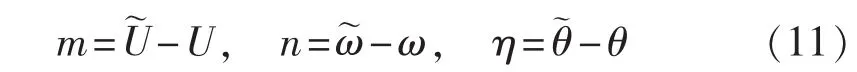
代入式(10)可得:
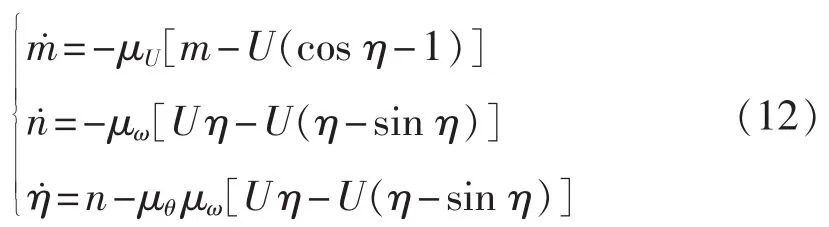
式(12)的每一项由两部分组成,即线性部分与非线性部分。考虑线性化的局部分析以及在实际系统中存在的低通滤波器性质,忽略非线性和2倍频部分,可以将式(12)简化为:

在式(13)中,幅值的动态响应含有一个负的实特征根 λU=-μU,对应时间常数τU=μU。 而频率/幅值的动态响应可以用下式表示:

由式(14)可知,在特征根的各系数中包含了输入信号的幅值,其是时变的,导致系统是非线性的。因此在频率环的输入信号中除以输入信号的幅值,从而实现解耦的目的。由此所提出的TPSF-EPLL经过修改后变为图2的形式。
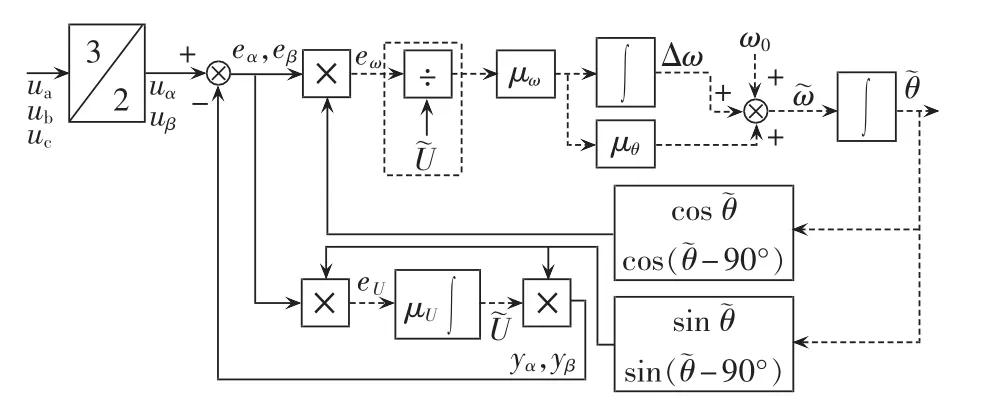
图2 修改后的TPSF-EPLLFig.2 Revised TPSF-EPLL
由于 μθ、 μω、U 均为正数,可得式(14)的特征根均在左半平面,因此该式能够证明此系统的局部稳定性。
在式(14)中,由于幅值环独立于频率环,因此只考虑幅值环的动态响应就能够获得整个系统的动态响应。幅值的动态响应含有一个负的实特征根λU=-μU,对应时间常数τU=1 /μU。 在实际系统中,调整时间 Ts=5τU,因此,对于 50 Hz系统,若 μU=125,则τU=1 /μU=0.008(s),Ts=5τU=0.04(s),相当于2个基波周期。对于频率环,由式(14)可知,频率环为典型的二阶系统,综合考虑其快速性和暂态性能,本文选择临界阻尼状态,即使其具有2个相等的实根,则有 ζ=1,ωn=ω0=314 rad /s,从而有 μθ=2ζ/ωn≈0.006,μω=8ζω2n/3≈262 922。
2 非理想电网条件对锁相环的影响及其抑制
在实际系统中,电网电压通常不是理想正弦波,而是包含负序、零序分量和谐波。下面分析这些非理想因素对锁相环性能的影响进而给出相应的解决方案。考虑上述非理想因素的输入信号表示为:
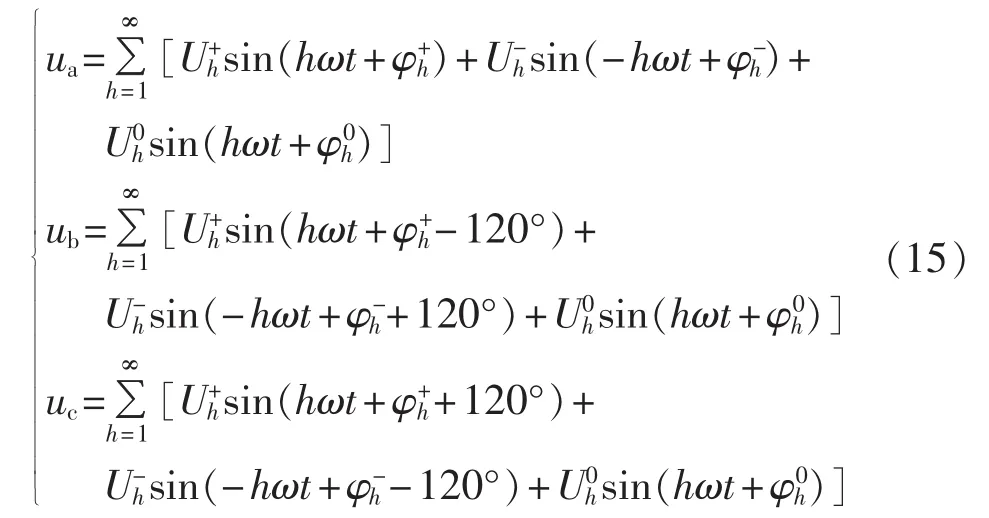
其中,U+h、U-h、U0h以及 φ+h、φ-h、φ0h分别为 h 阶正序、负序和零序分量的幅值和相角。当h=1时,各个变量代表基波成分。经过3/2坐标变换后,得到新的输入信号为:
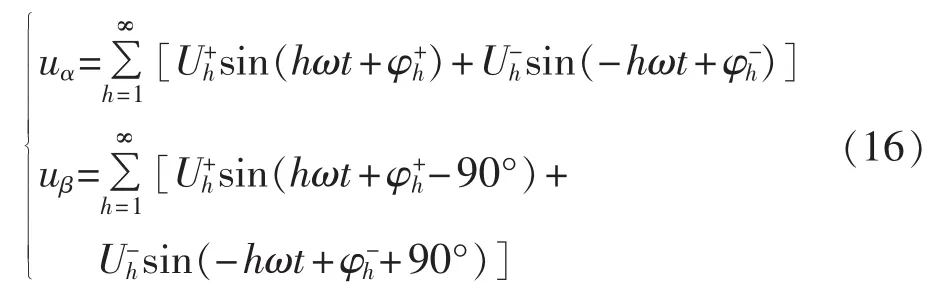
此时新的输入信号不存在零序分量。根据图1,假设此时锁相环的输出电压跟随正序基波分量,频率环和幅值环的输入信号变为:
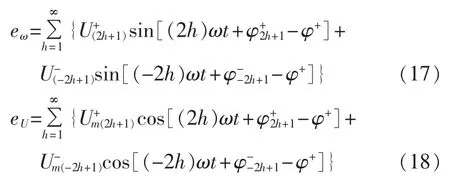
由式(17)、(18)可知,在这 2 个环节的输入信号中会产生周期波动,最低次为2次。这一波动将导致锁相环估计的幅值、相角和频率同样存在周期波动。
因此本文将Goertzel滤波器引入到频率环和幅值环的输入侧,用于滤除不平衡和谐波的影响。改进后的锁相环如图3所示。
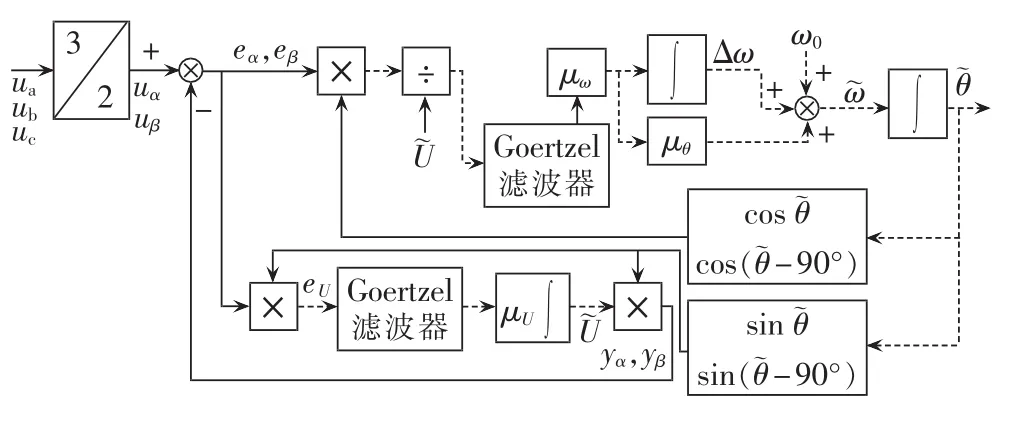
图3 包含Goertzel滤波器的TPSF-EPLLFig.3 TPSF-EPLL with Goertzel filter
Goertzel滤波器是由滑动离散傅里叶变换所推导出来的一种滤波器,根据滑动离散傅里叶变换算法,采样点数为N,某一时刻q第k个频率单元的频谱值表示为[17]:
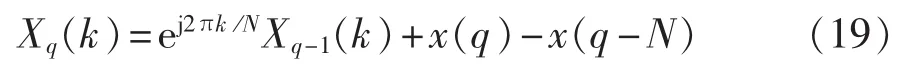
其中,x(q)和 x(q-N)分别为 q 和 q-N 时刻的采样值。因此,当所要得到的频率为直流时,令k=0,并且通过z变换,可以得到Goertzel滤波器在z域下的表达式为:
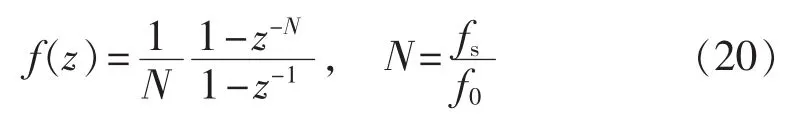
其中,fs为采样频率;f0为基波频率;1/N是为了补偿滤波器带来的增益变化的系数。通过以上滤波器,可以滤除所有频率为下式所示的谐波:
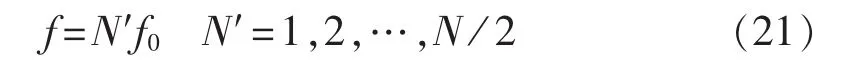
由于本文需要滤除频率环的比例积分控制器输入信号中的交流成分,而该交流成分的频率分布为原始输入信号的2倍频的整数倍,中国电网额定频率为50 Hz,故设定f0=100 Hz。图4为采样频率为10 kHz、N=10000/100=100 时 Goertzel滤波器的 Bod图。可见,该滤波器在100 Hz及其倍数次频率处的增益变为-150 dB,说明对2倍频及其倍数次谐波具有较好的衰减作用,而在其他频段增益接近于1,衰减很小。该滤波器能够达到上述滤波目的。
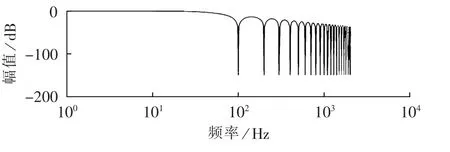
图4 Goertzel滤波器的Bode图Fig.4 Bode diagram of Goertzel filter
3 实验结果与对比
本文提出一种新的锁相环结构及相应的非理想输入条件下的性能优化方案,需对其稳态跟踪精度、动态响应性能以及在非理想输入条件下的幅值、相角、频率和跟踪性能进行实验验证。搭建了基于浮点型DSP芯片(TMS30F28335)的实验平台用于对所提出TPSF-EPLL的性能进行验证。考虑到实际电网电压波形是不可控的,难以对所提TPSF-EPLL的性能进行全面检验,因此将三相输入信号在DSP中用软件产生,以便于产生阶跃变化以及加入不平衡和谐波。三相输入信号和锁相环的输出信号经DA转换芯片(DAC7515)将数字量转换为模拟量以便于通过示波器观察。三相输入信号的初始条件为:幅值为1 p.u.,频率为50 Hz,三相信号保持对称且不包含谐波。
首先对其在理想输入条件下的稳态跟踪精度和动态性能进行实验验证。考虑到在实际应用中,最常见的就是输入信号发生幅值、相角和频率的突变,实验方案为:在初始阶段,三相输入信号保持平稳,锁相环达到了稳态,即已经获得了三相输入信号的幅值、相角和频率信息,而在某一时刻分别将幅值对称突减40%、相角对称跳变40°以及频率跳变10%,经过5个基波周期后幅值和频率均恢复为初始状态。下面给出完整的实验结果,包括稳态阶段和突变后的动态变化过程直至达到新的稳态的完整过程的波形。实验波形分别如图5—7所示,分别对应三相输入波形、三相输入的两相坐标变换波形、两相估计波形、估计的幅值和幅值误差、估计的频率和频率误差、估计的相角和相角误差。通过稳态阶段的波形能够分析其稳态估计精度,而通过动态过程的波形能够对其动态响应性能进行评价。
由图5—7可知,在系统处于稳态时,所估计的幅值、相角和频率误差均为零,说明所提出的TPSFEPLL很好地实现了对输入信号同步信息的估计。在幅值发生突变时,最大幅值误差等于相应的突变值,经过短暂的过渡过程(大约20 ms),幅值误差等于零,说明跟随上了新的幅值;相角和频率均产生小的波动,经过5 ms恢复到稳态值。在相角跳变时,最大相角误差等于跳变值,动态响应时间约为20 ms;所估计的幅值和频率均产生瞬态波动,最大瞬态幅值误差为0.08 p.u.,经过5 ms恢复到稳态,频率误差较大,超过20 Hz,这是由于输入信号的瞬态相角跳变在频率环的输入侧产生了较大的误差信号,经过10 ms重新恢复到稳态。在频率跳变时,最大频率误差等于跳变值,动态响应时间约为20 ms;幅值环几乎没有受到影响;所估计的相角产生瞬态波动,最大瞬态相角误差为4°,经过20 ms恢复到稳态值。
进一步与包含陷波滤波器的双同步旋转坐标系下的锁相环和三相增强型锁相环的控制性能和计算量进行了对比。为节省篇幅,只把这2种传统锁相环和所提出TPSF-EPLL的动态性能数据以及代码执行时间列于表1。表中,Tset为动态响应时间;ΔUm、Δθm、Δfm分别为动态过程中幅值、相角和频率的最大误差。由表1可知,所提出的TPSF-EPLL获得了和传统锁相环相近的动态控制性能,包括动态响应时间和各估计量的最大瞬态误差。由于所提出的TPSFEPLL在两相静止坐标系下进行运算,因此总执行时间减少约40%,显著降低了对控制器资源的占用。
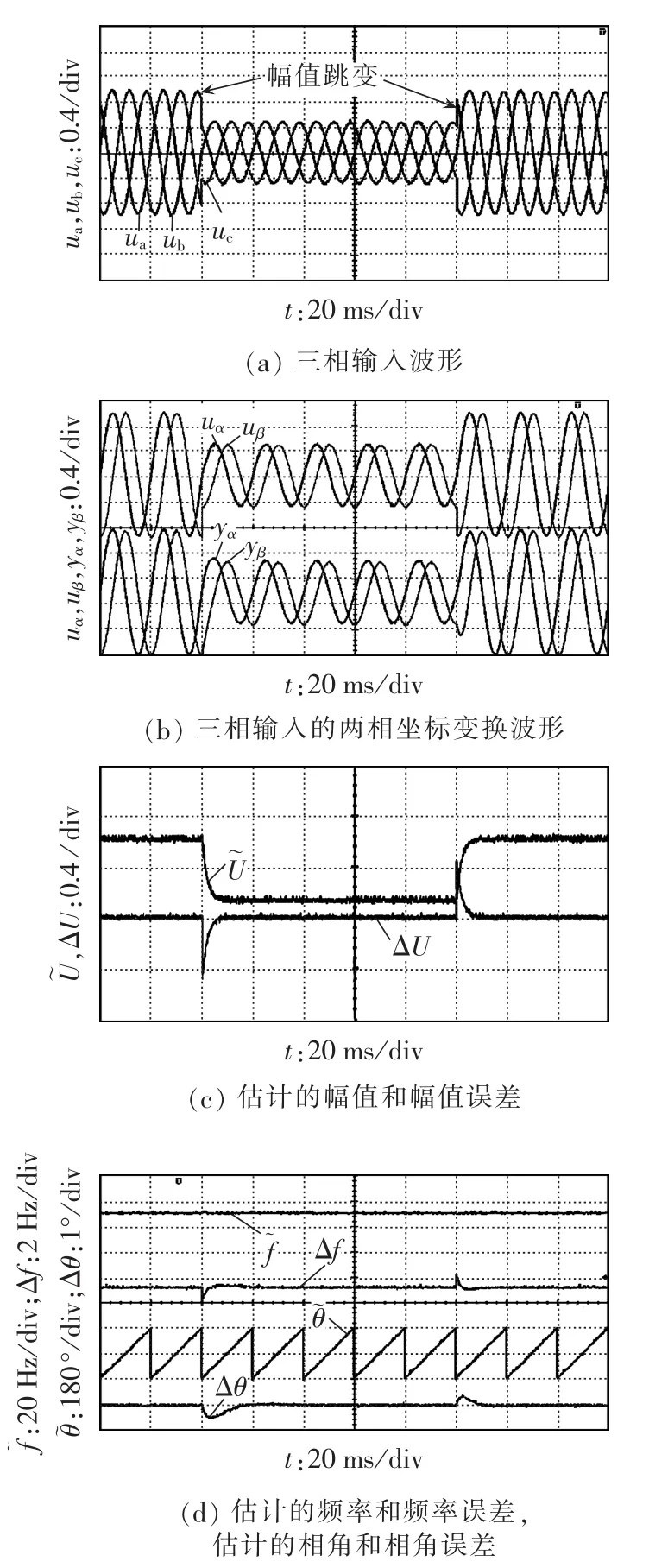
图5 幅值突变下的动态响应实验波形Fig.5 Experimental waveforms of dynamic response to amplitude step change
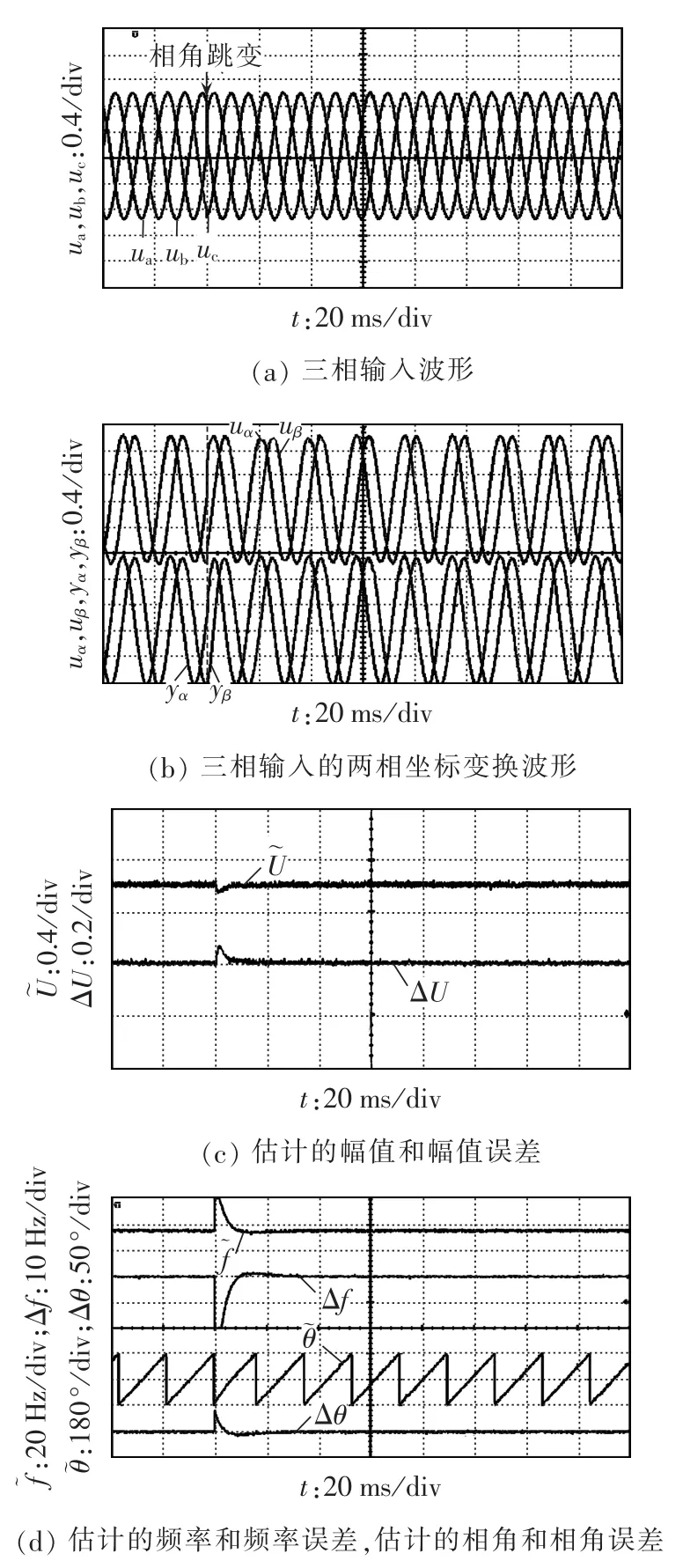
图6 相角跳变下的动态响应实验波形Fig.6 Experimental waveforms of dynamic response to phase angle step change
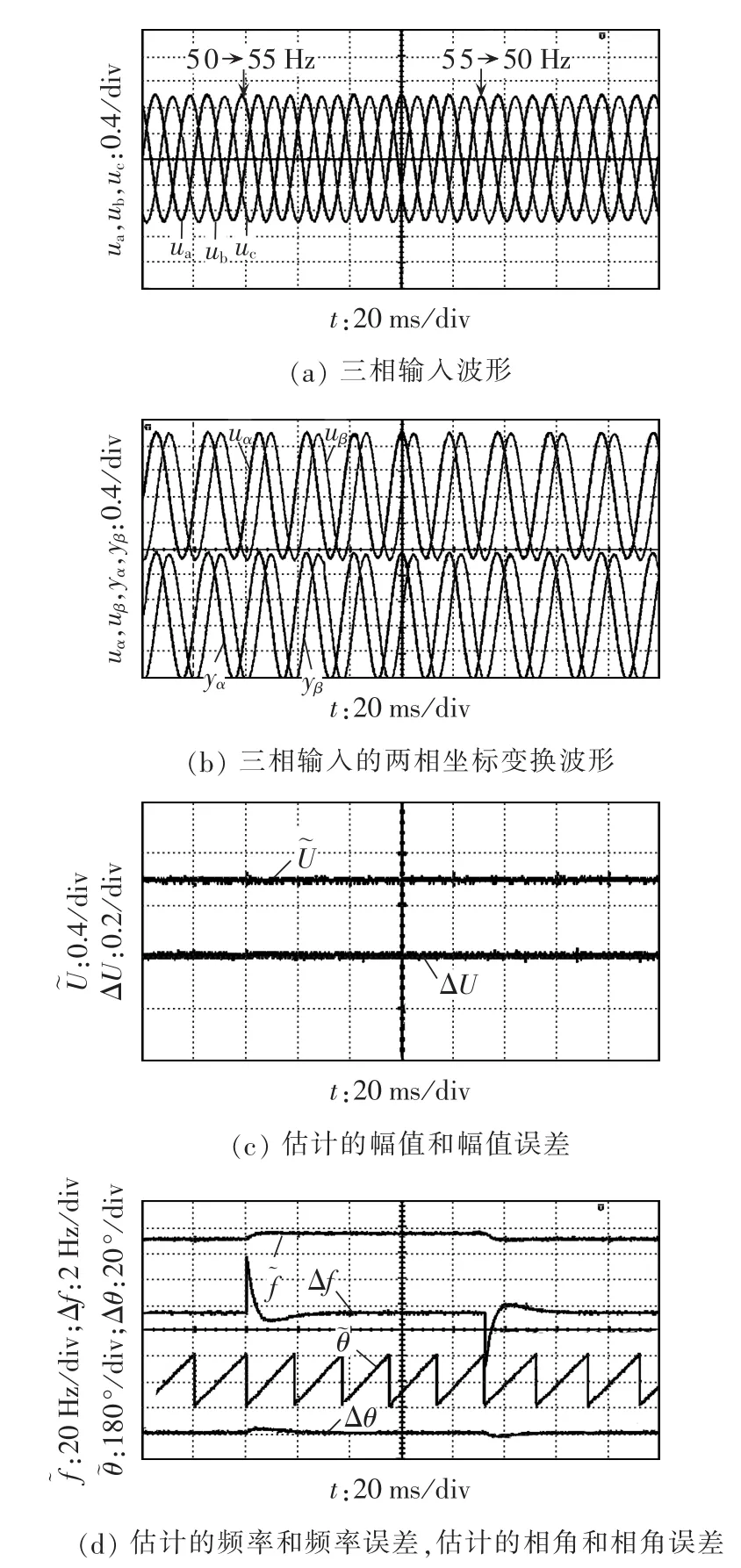
图7 频率跳变下的动态响应实验波形Fig.7 Experimental waveforms of dynamic response to frequency step change
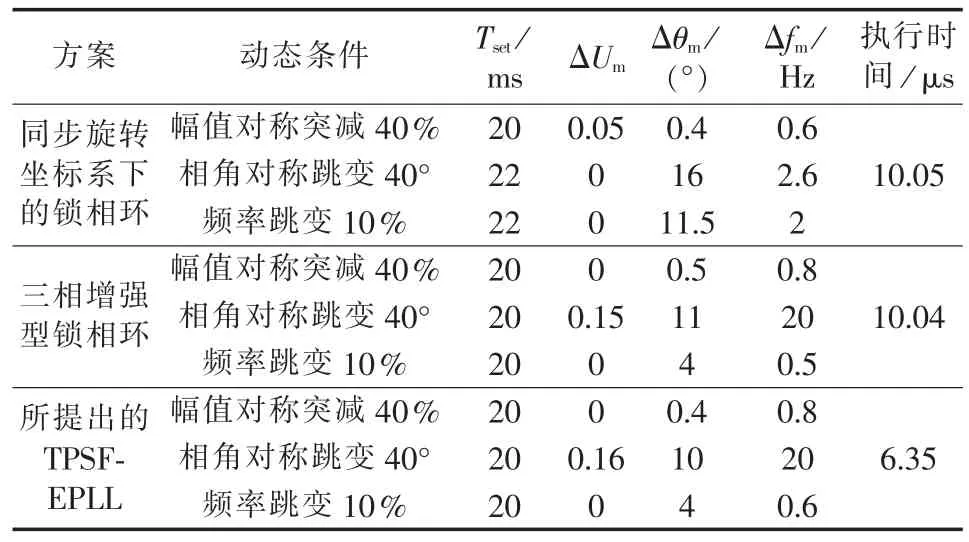
表1 3种锁相环的动态数据及代码执行时间Table 1 Dynamic data and code execution time for three kinds of PLL
最后对加入滤波器后的所提出的TPSF-EPLL在输入信号存在谐波和不平衡时的锁相性能进行了实验验证。为验证其抗谐波扰动性能,实验条件设为:将5、7、11以及13次谐波加入输入信号,幅值均为0.1 p.u.,在某一时刻突然加入连续5个基波周期的谐波以后输入信号恢复为理想正弦波形。图8给出了相应的实验波形,由图可知,在突加谐波时,幅值环几乎没有受到影响,而所估计的相角和频率中包含周期波动,经过大约40 ms以后系统达到稳态,所估计的幅值、相角和频率信息中均不包含输入谐波成分,滤波器的加入明显抑制了谐波的影响。需要说明的是,所估计的相角和频率中存在的短时周期波动是由Goertzel滤波器的工作特性所决定的。最后对所提出的TPSF-EPLL在输入信号不平衡情况下的性能进行实验验证,实验条件为:将a相输入信号的幅值变为0.1 p.u.,b相相角跳变80°。等效为正序相量为U+=0.536∠-37.71°p.u.,负序相量为U-=0.129∠-52.8°p.u.。同样在5个基波周期以后输入信号恢复为理想三相对称正弦波形。实验波形如图9所示。由图9可知,输入信号突然变为不平衡时,所估计的幅值、相角和频率均产生较大瞬态误差,经过大约30 ms的动态过程,系统达到稳态,此时在所估计的幅值、相角和频率波形中均不存在周期波动,说明滤波器的加入很好地抑制了不平衡造成的影响,获得了较好的锁相性能。
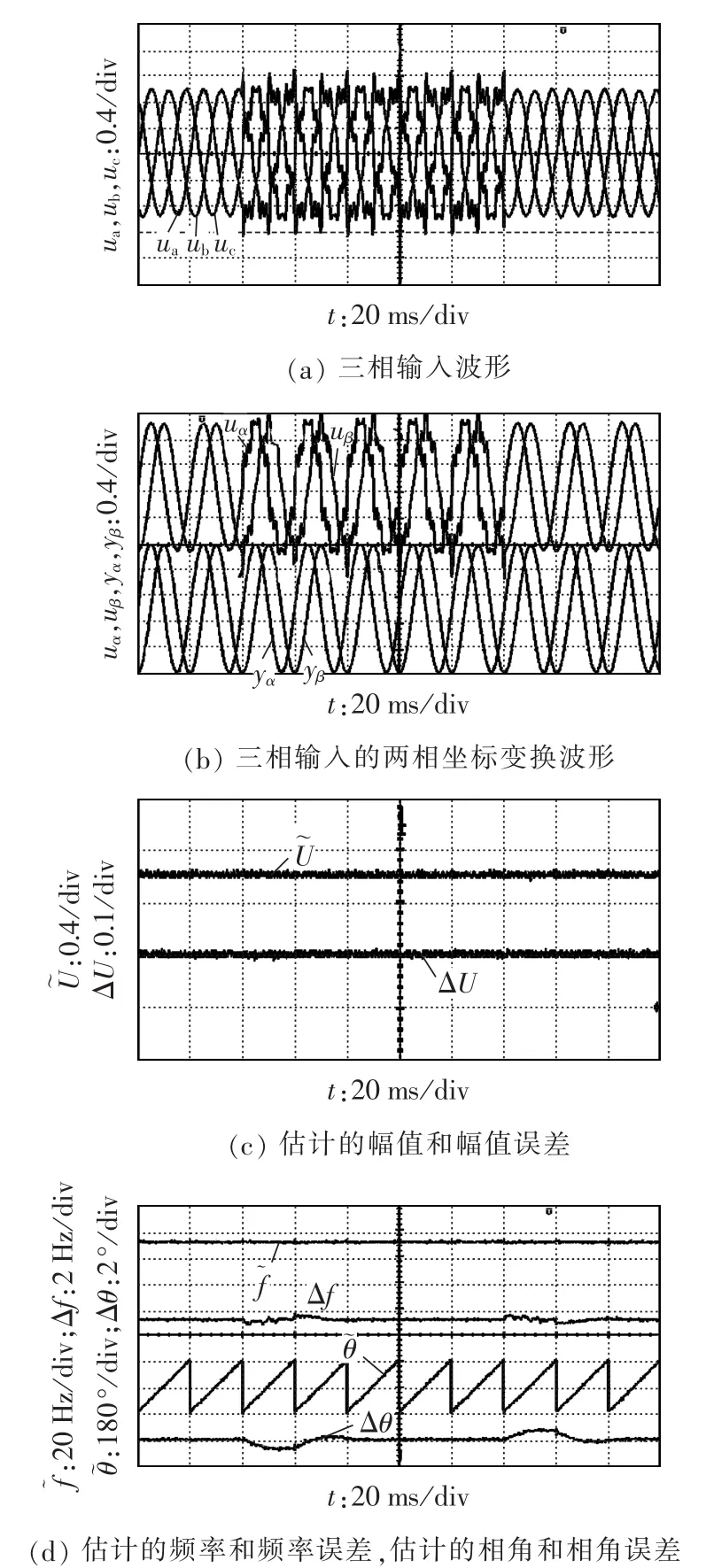
图8 谐波输入条件下的所提出TPSF-EPLL的实验波形Fig.8 Experimental waveforms of proposed TPSF-EPLL for input signals with harmonics
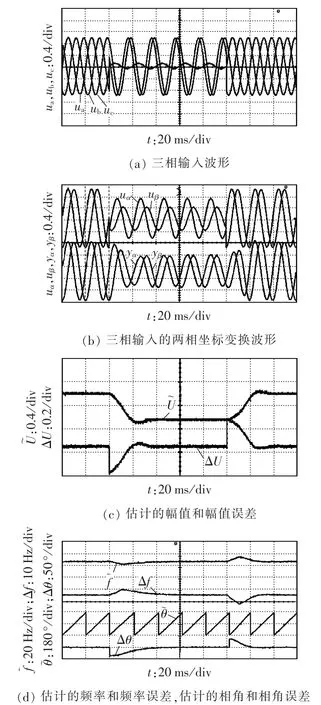
图9 不平衡输入条件下的所提出TPSF-EPLL的实验波形Fig.9 Experimental waveforms of proposed TPSF-EPLL for unbalanced input signals
4 结论
a.提出了TPSF-EPLL用于三相电网电压的信息估计,包括幅值、相角和频率,相应的实验结果表明,所提出的TPSF-EPLL具有和现有三相锁相环相近的动静态性能,而计算量降低约40%;
b.通过将Goertzel滤波器引入到所提出TPSFEPLL的频率环和幅值环,有效抑制了输入谐波和不平衡的影响,稳态估计信息中已不再含有周期波动;
c.所提出的TPSF-EPLL有效减小了控制器的计算负担,更加有利于与并网型电力电子电能变换系统相融合,具有较好的应用前景。
