结合风电功率超短期预测值偏差的实时市场调度

江岳文，温步瀛

（福州大学 电气工程与自动化学院，福建 福州 350108）

0 引言

由于天气、电网故障等偶然因素，日前市场的发电计划与实际负荷偏差较大时，需要启用实时平衡市场，以平衡不平衡的出力，维持电力系统正常稳定运行。实时市场一般已经非常接近实际运行时间点，其负荷数据来自于超短期负荷预测数据[1]，由于时间的逼近和相关负荷预测因素的明朗清晰化，超短期预测的负荷已经能高精度跟踪电力系统实际负荷[2-3]。因此，超短期负荷预测误差带来的不确定性因素基本可以忽略，即把超短期负荷预测作为一个确定值，不考虑负荷预测误差的影响。

随着风电的大规模并网，风电在节省化石能源、减少有害气体排放的同时，也对电力系统的运行造成了一定的影响，如潮流的波动、电压质量变化、辅助服务的增加、调度不确定性等[4]。这些影响的根源来自于风电的不可准确预测性。按照预测时间尺度的不同，风电功率预测一般可分为超短期预测、短期预测、中期预测和长期预测。短期预测一般是提前1～48 h（或72 h）的预测，其目的是为了向电网调度提供调度依据及满足风电参与竞价上网的需要，多用在日前市场中；超短期预测一般是提前几十分钟的预测，其目的是为了满足风电机组控制的需要，优化电力系统运行，多用在实时市场中[5]。目前，风电出力预测技术虽不断地提高，但预测结果仍然不理想，如短期预测精度只能达到80% 多[6]，超短期预测精度较短期预测精度有所提高，但偏差仍有9%左右[7]。因此，在实时市场中，超短期的风电点预测值尚不能作为一个确定的值，需要考虑预测偏差，以满足实时平衡市场调整发电计划出力的需要，减少功率偏差缺额。

当超短期负荷预测与原有发电计划出现偏差时，文献[8-9]探讨采用发电计划偏差调整措施进行功率的平衡，并利用改进的粒子群算法进行求解，尚未考虑风电因素。考虑风电预测偏差的日前市场经济调度文献较多，如文献[10-12]考虑了风电的预测偏差，在风速基于Weibull分布基础上，求出风电预测出力偏差期望值，探讨含有风电的经济调度模型；文献[13]根据风电功率预测误差随着时间尺度的减小而减小、预测精度逐渐提高的特性，提出计及风电预测误差带的日前和日内调度计划。日前市场时间跨度为24 h，风速的分布特性多采用Weibull分布来计算风电预测偏差期望值。但当关注超短期风速对电网调度或运行的影响时，就需要利用更短周期内的风速分布统计规律[14-15]。

本文考虑在风速超短期预测的基础上，依据风速与功率关系的表达式，得出风电功率超短期预测值。基于风速的正态分布特性，推导风电场功率的概率密度函数和概率分布，并在实时平衡市场机组出力调整费用模型中引入风电出力预测偏差造成的成本，考虑风速分布特性、风电预测值、惩罚成本系数等对实时市场的影响。

1 风速满足正态分布的风电场功率特性分析

对大量实测数据的统计结果表明，较长时间内风速的随机分布近似服从Weibull函数。如果统计风速数据时间较短，则利用正态分布来描述风速的概率分布可能更接近其真实分布函数[15]，其概率密度函数为：

2 实时平衡市场模型

负荷预测技术的不断提高和负荷本身的规律性，使得负荷预测偏差比风速预测偏差要更小，超短期负荷预测值基本可以替代实际的负荷值。因此，在目标函数中忽略了负荷预测偏差的影响。风速预测随着预测时间的缩短，预测精度会提高。但是由于风速本身的特性，即使缩短预测时间也会存在较大的偏差，因此需要考虑风速预测偏差对系统功率不平衡的影响。故实时平衡市场出力偏差调整费用目标函数为：

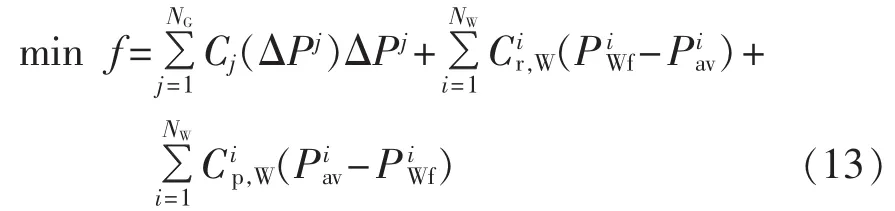
其中，NG、NW分别为常规发电机组的台数和风电场的个数；Piav为结合风电场i风速概率分布的一个随机值，变化范围为0≤Piav≤PiWN，其值的大小与风速的概率分布有关。

在式（13）中，等号右边第一项表示常规机组因负荷和风电预测出力的偏差而造成的系统实际出力和日前市场上的计划出力不一致，因此形成上调出力或下调出力费用，其中Cj（ΔPj）为实时市场中常规机组出力调整费用报价（单位为元／MW），具体如下：

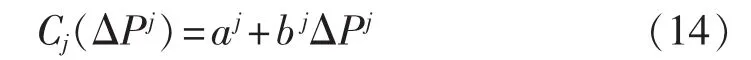
其中，aj、bj为常规机组 j报价函数系数；ΔPj为机组j在实时市场中上调或下调的出力（单位为 MW）。

在式（13）中，等号右边第二项表示风电出力超短期预测值过高而引起的备用成本的增加，函数形式如下：

3 算例分析

网络数据采用IEEE 30节点系统数据，日前市场计划负荷为283.4 MW。假设 λir=400 元 ／（MW·h），λpj=400元 ／（MW·h）。 发电机实时市场报价函数和相关参数见表1。实时市场某一时刻t预测负荷为307.5 MW，则实时市场的负荷预测偏差为24.1 MW，增加负荷的节点分别是：节点2增加4.5MW，节点5增加7MW，节点8增加10MW，节点21增加2.6MW。风电场接入节点为节点6，日前市场预测的风电出力为32 MW，实时市场预测的风电出力值为27.5 MW，则实时市场功率不平衡量为28.6 MW。根据该地区与时刻t较短时间段的风速数据，分别用正态分布和Weibull分布概率进行比较，见图1和图2。根据比较结果，风速特性利用正态分布来描述比较吻合。采用极大似然法进行参数拟合，得到正态分布参数μ=5.1041，σ=0.7835。风电场其他参数为：PiWN=50 MW，viin=3 m ／s，viN=15 m ／s，viout=25 m ／s。

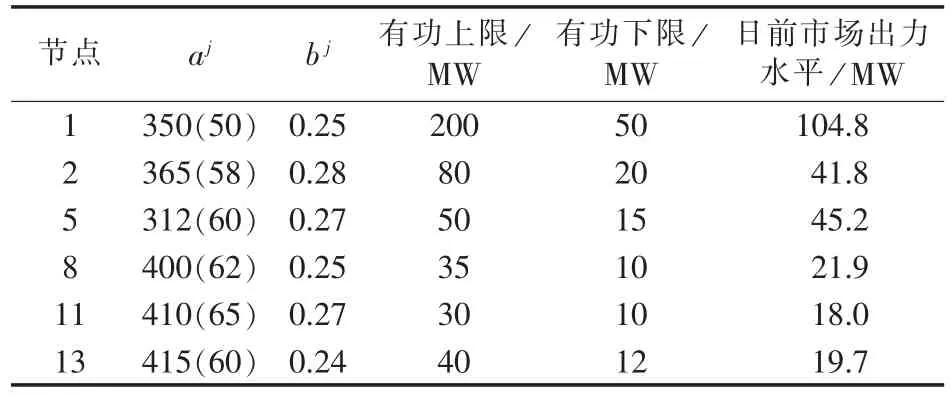
表1 发电机组实时市场报价函数和相关参数Table 1 Bidding function of generators in real-time market and relevant parameters

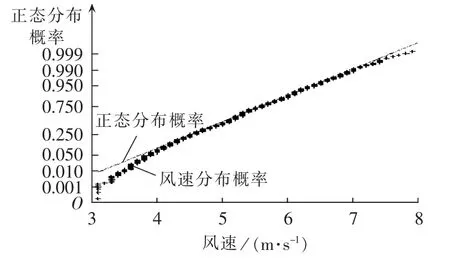
图1 实测风电场风速分布与正态概率分布比较Fig.1 Comparison between measured wind speed distribution in wind farm and normal distribution

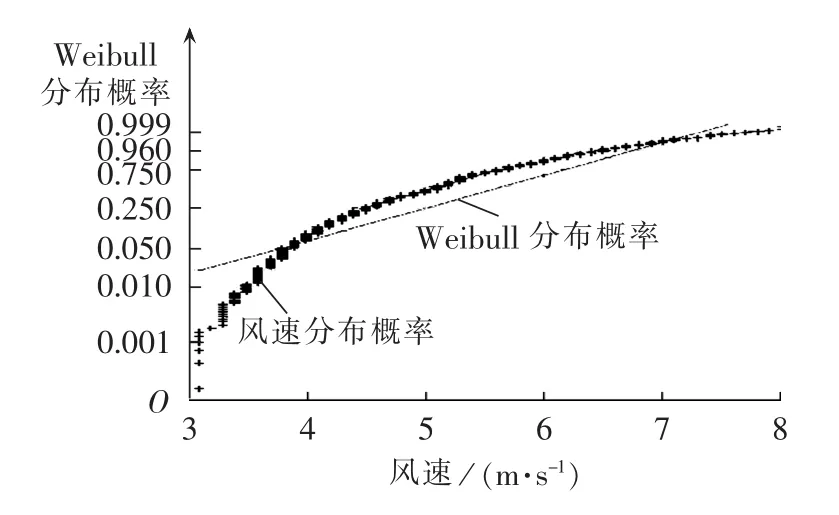
图2 实测风电场风速分布与Weibull概率分布比较Fig.2 Comparison between measured wind speed distribution in wind farm and Weibull distribution

在实时市场中进行超短期风速预测，依据式（3）计算出预测功率，根据式（10）—（12）可得出未来实际风电功率与预测功率偏差的概率。图3显示了风电场未来实际出力PiWr大于预测功率的概率，其中超短期预测风速间隔为10 s，预测风电功率点数为120个。由于预测功率的变化，每一个测点偏差概率也随之变化。

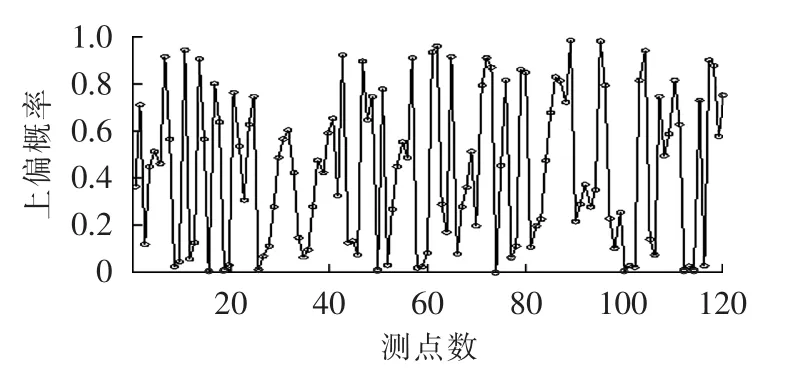
图3 功率偏差概率Fig.3 Probability of power error

根据上述出力调整模型，利用粒子群算法进行求解。各节点上发电机组出力调整量如表2所示，风电高估、低估出力期望值以及高估成本和总成本分别为18.63 MW、0 MW、7451.9元、17546元。

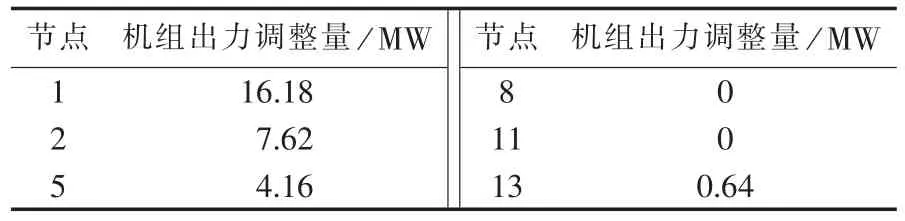
表2 算例优化结果Table 2 Optimized results of given case

为了进一步深入探讨文中相关的参数对总成本及高估出力和低估出力期望值的影响，本文从以下几方面作优化分析。

a.不同的风速分布特性及风电功率预测值对实时市场的影响。

设 λri=λpj=400 元 ／（MW·h）， μ=5.104 1，σ 取0.7835和1.5时，总成本、高估出力和低估出力期望值的变化见图4和图5。

同样，设 λri=λpj=400 元 ／（MW·h），μ 取 5.1041和7.1041，σ=0.7835，总成本、高估出力和低估出力期望值的变化见图6和图7。

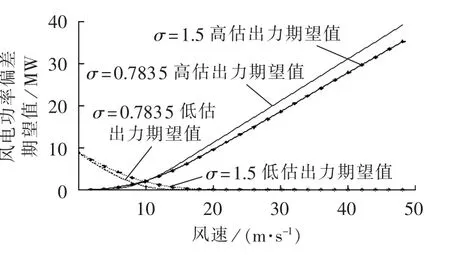
图4 σ及预测风速的变化对功率偏差期望值的影响Fig.4 Impact of σ and wind speed forecast variation on power error expectation

图5 σ及预测风速的变化对成本的影响Fig.5 Impact of σ and wind speed forecast variation on cost

图6 μ及预测风速的变化对功率偏差期望值的影响Fig.6 Impact of μ and wind speed forecast variation on expectation of power error

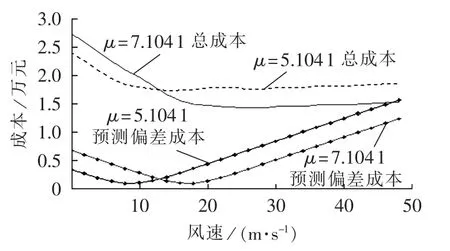
图7 μ及预测风速的变化对成本的影响Fig.7 Impact of μ and wind speed forecast variation on cost

不论σ或μ取值大或小，随着超短期风电功率预测值的增加，低估出力皆减小直至0，高估出力从0不断增加，最高接近40 MW。随着σ和μ的变大，低估出力期望值在增加而高估出力期望值减小，见图4和图6。

总成本曲线先下降后上升，下降段是比较平滑的曲线，后半段总体趋势是上升的，但上升速度不如下降段变化速度快。随着实时市场中风电出力预测值的上升，常规机组的出力调整费用一直是单调下降的，总成本开始由以常规机组出力调整费用为主逐步过渡到由风电预测偏差引起的惩罚成本为主。风电预测偏差引起的惩罚成本是一个先降后升的曲线，如图5和图7所示。因此，当偏差成本上升曲线变化的成本小于常规机组出力调整费用下降成本时，总成本曲线就会产生一个总体趋势向上但预测点上的值会稍回落的非平滑曲线。随着σ的变大，总成本曲线在转折点前稍大，转折点后反而更小了，原因是随着σ的增加，高估出力期望值减小，故功率偏差成本也减少了。μ的变化对成本的影响与σ一样，只是影响的效果会更明显。

b.不同的λir、λpj及风电功率预测值对实时市场的影响。

设μ=5.1041，σ取 0.7835时，总成本、高估出力和低估出力期望值的变化见图8。

图8 λir与λpj及预测风速的变化对总成本的影响Fig.8 Impact of λir ，λpjand wind speed forecast variation on total cost

随着实时市场对风电预测出力的增加，低估期望值减小，高估期望值增大。在风电预测出力较小时，低估期望值远远大于高估期望值。因此，仅弃风成本系数λpj下降的成本曲线的成本最低；随着风电预测值出力的增加，高估期望值不断加大，低估期望值减小到0，故仅有备用成本系数λir下降的成本曲线与另外2条成本曲线没有重合，而且下降趋势一直在延伸，在额定功率范围内尚没有拐点。由此可见，λri越小，高估风电功率预测值对平衡市场中因出力不平衡而产生的成本费用是有利的；而当λpj越小时，低估风电功率预测值对出力不平衡而产生的成本费用是有利的。

4 结论

本文考虑超短期风电功率预测的不确定性，在优化常规机组出力调整费用的同时，结合风电预测功率的高估出力期望值和低估出力期望值对系统运行成本的影响，构成整体以多成本为目标的函数。通过算例，分析不同的风电预测出力、风速分布特性参数、备用成本系数、弃风成本系数对成本以及出力偏差期望值的影响，得出如下结论。

a.详细推导了较短时间内风速满足正态分布的风电场功率分布表达式以及风电场未来实际出力与预测功率的偏差概率。

b.把风电偏差成本与常规机组出力成本作为实时平衡市场上总的调整成本，该成本随着正态分布参数标准差的变大先增大后减小，另一个参数平均值的影响与之类似。总成本随着风电功率预测值的增大而先单调减小再锯齿波式上升。偏差成本随着风电预测功率的增加，先单调下降而后单调上升，具有明显的拐点。

c.风电预测功率高估出力期望值随着标准差的增大先略有增大而后减小，低估出力期望值随着标准差的增大而增大，另一个参数平均值的影响与之类似。随着风电预测功率的增加，低估出力逐渐减小到0，高估出力由0逐渐增大。

d.备用成本系数越小，高估风电预测值对平衡市场中因出力不平衡而产生的成本费用是有利的；弃风成本越小，低估风电预测值对出力不平衡而产生的成本费用是有利的。