基于分岔理论研究励磁饱和环节对系统电压稳定的影响

李国庆，张 浩，李 江，王义伟，张 鹏

（东北电力大学 电气工程学院，吉林 吉林 132012）

0 引言

随着电力市场化改革的不断深入，现代电力系统已越来越接近其运行和控制极限，电网中电压失稳乃至电压崩溃的事故时有发生，因此电压稳定问题成为了学术界日益关注的焦点。电力系统具有强非线性特性，因此非线性分析方法的介入显得尤为重要。分岔理论作为分析和研究非线性系统结构稳定性的基本方法[1-3]，近些年来在电力系统电压稳定问题研究中取得了丰硕成果。文献[4-6]研究了局部分岔理论在电力系统稳定分析中的应用。文献[7-9]从负荷角度考虑了几种典型模型对系统电压稳定的影响。文献[10]基于Walve综合负荷模型，采用分岔理论对一种典型电力系统模型进行了电压失稳机理研究。文献[11]介绍了电力系统电压稳定分析中的多种分岔现象及其与电压失稳之间的关系。文献[12]基于分岔理论探讨了发电机数学模型对系统动态电压稳定性的影响。文献[13-16]也应用分岔理论给出了电力系统的一些分岔分析结果。这些研究均展现出了电力系统的复杂非线性动力学特性。

针对电力系统可能出现的不稳定现象，分析运行和控制极限发生时的动态过程，弄清含励磁饱和环节的电力系统稳定性问题，对电力系统的安全稳定运行具有重要的理论和现实意义。文献[17]研究了发电机励磁顶值和PSS回路对电力系统的振荡失稳和混沌现象的影响。文献[18]以一个典型的电力系统模型为基础，分析了考虑励磁限制所导致的各种分岔行为。为了研究方便，对于励磁限制器的限制作用采用光滑的函数进行模拟，但由此所带来的计算误差是不可避免的。因此，本文采用降低方程组维数的方法来准确地模拟励磁限制器的限制作用，进而研究励磁饱和环节对系统电压稳定的影响，并在此基础上逐渐降低励磁电压顶值，对比分析其对系统动态行为的影响。

本文虽以一个简单的单机3节点电力系统模型为研究对象，但此研究方法、结论同样可以推广到多机系统。文献[19-20]基于极限诱导分岔，分别采用单机和多机系统模型研究了发电机无功极限对系统电压稳定的影响，此文献类比于本文的研究内容和结论。文献[21]采用IEEE 14节点网络数据，研究了发电机最大励磁极限对系统电压稳定的影响，所得结论与本文研究成果一致。文献[22]研究一个234节点的电力系统，成功地搜索出了静分岔点。

1 含励磁饱和环节的系统模型

电力系统电压稳定研究所采用的数学模型一般可以由一组微分-代数方程组来描述：

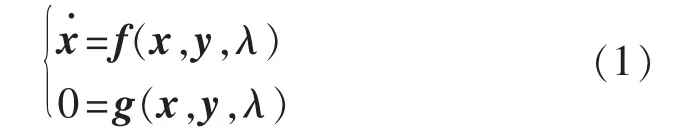
其中，x∈Rn和y∈Rm分别为系统的微分变量和代数变量；λ∈R为电力系统的某一控制参数；微分方程组f（·）描述了电力系统元件的动态行为；代数方程组g（·）由电力系统潮流方程和描述微分变量与代数变量关系的方程组成。

文中采用简单的单机3节点电力系统模型。该模型由1台发电机、1条负荷母线和1条无穷大母线组成，如图1所示，详细参数可参阅文献[23]。

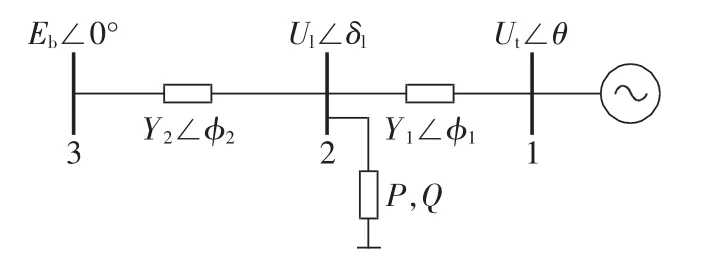
图1 系统模型示意图Fig.1 Schematic diagram of system model

1.1 发电机模型

a.转子侧方程。

发电机转子运动方程如下：

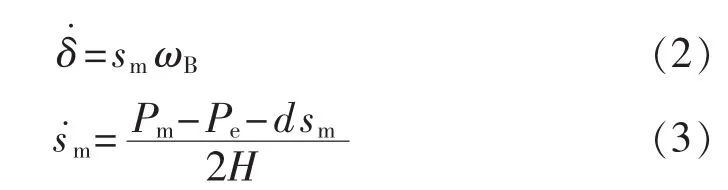
其中，sm为转差率；ωB为额定角频率；Pm为机械输入功率；Pe为电磁功率；δ为发电机功角；H为机械转动惯量；d为机组阻尼系数。

描述励磁绕组和q轴阻尼绕组的暂态过程方程如下：

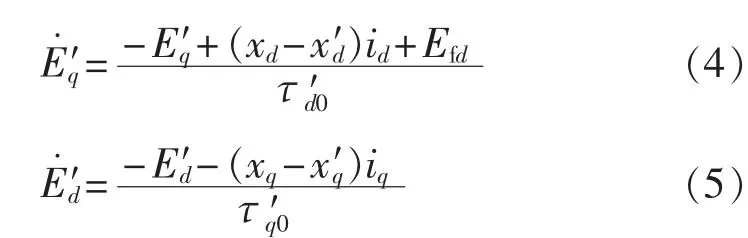
其中，E′q和 E′d分别为 q 轴和 d 轴暂态电势；Efd为励磁电势。

发电机的输出功率为：

b.定子侧方程。

忽略定子电阻及其暂态过程，定子侧方程如下：

1.2 励磁系统方程

发电机励磁系统用一个高增益的单时间常数自动电压调节器（AVR）和限制器表示，传递函数框图如图2所示。该励磁系统的数学模型如下：

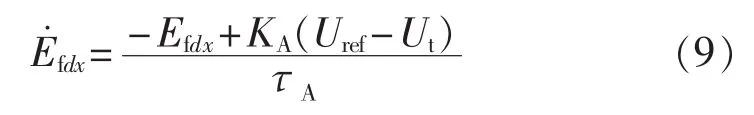
其中，τA和KA分别为励磁系统调节器的时间常数和放大倍数；Ut为发电机机端电压。

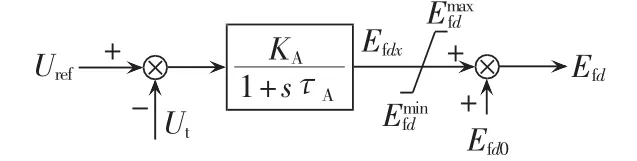
图2 励磁系统框图Fig.2 Block diagram of excitation system

图2中的限制器可以用式（10）描述：

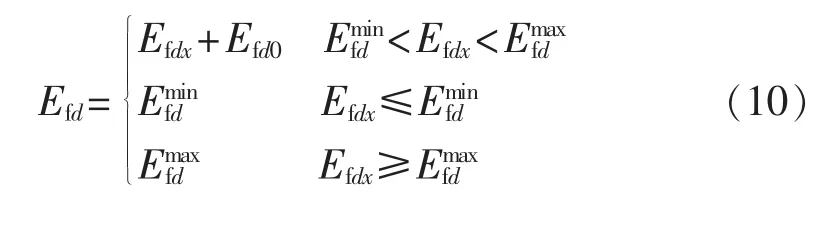
1.3 负荷模型

负荷节点采用描述大扰动下感应电动机动态行为的Walve综合负荷模型，其表达式为：

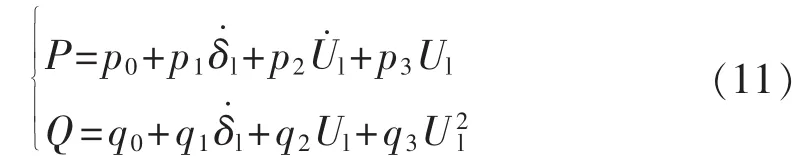
其中，Ul和δl分别为负荷节点的电压和相角。

1.4 网络模型

采用图1中的符号，不难得到以下网络方程：

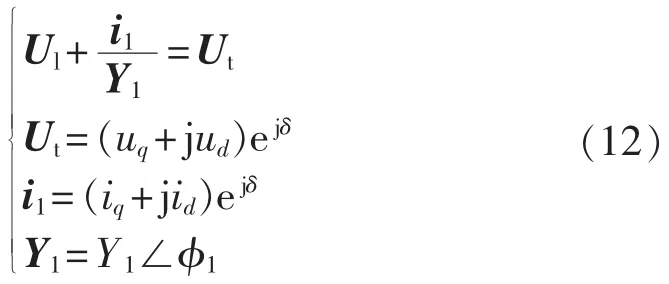
令 a=Y1Ulcos（δl-δ），b=Y1Ulsin（δl-δ），则有：

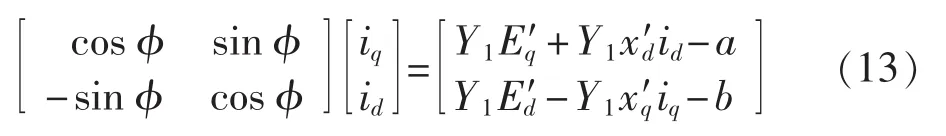
方程中规定的相角关系如图3所示。

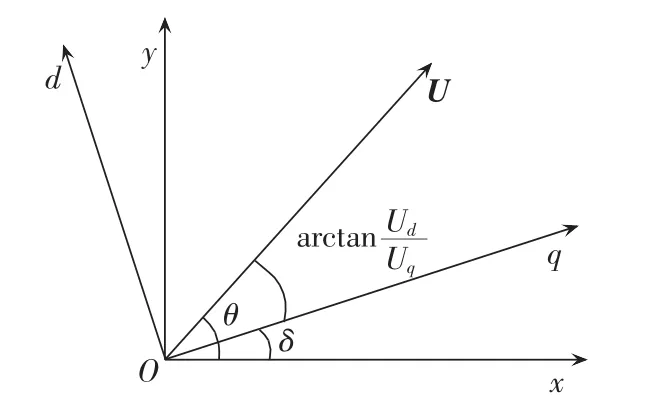
图3 方程中规定的相角关系Fig.3 Phase relationship stipulated in equations

1.5 全系统模型

母线2处的功率平衡方程为：

整理可得全系统的简化模型如下：

其中，x=[δ smE′qE′dδlUlEfdx]T；λ为分岔参数。图2中的限制器是一个窗口限制器，由于该模型非连续，无法用来进行分岔分析，本文采用降维的方法描述这一励磁饱和环节，即在励磁电压达到顶值时，不考虑式（9）的作用，并令式（4）中的励磁电压Efd等于励磁顶值。

假如考虑励磁饱和环节，且励磁顶值等于5 p.u.，从数学模型的角度而言，此时Efdx不再是微分变量，而式（4）也将变为：

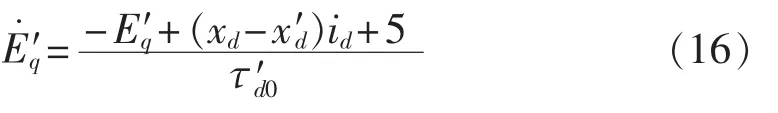
其他微分方程保持不变，由此可知微分方程组的维数降低了一维，此时的状态变量为：

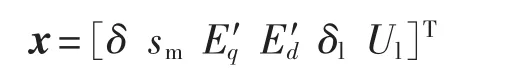
2 系统分岔分析

本节将利用分岔分析软件AUTO 07[24]，对图1所示系统进行分岔分析，在考虑励磁饱和环节及降低励磁电压顶值的前提下，阐述系统动态行为所呈现的差异。

2.1 不考虑励磁饱和环节时的分岔分析

根据Ul所代表的物理意义，当机械输入功率Pm变化使Ul处于稳定或不稳定平衡点时，对应于系统的电压稳定或不稳定状态。后面的分析中，Pm、Ul和Efdx均为标幺值；图中实线与虚线分别表示稳定、不稳定平衡点，曲线拐点为鞍结分岔点，实心小方框代表Hopf分岔点。

图4中点1是系统初始稳定平衡点，点3是励磁电压等于5 p.u.时的平衡点，曲线拐点4是鞍结分岔点。由图4和图5可以看出，随着分岔参数Pm的增加，系统在到达鞍结分岔点之前已经出现了Hopf分岔。可见，鞍结分岔点对应的机械输入功率值已不是系统安全运行的功率极限，单纯的鞍结分岔点已不能完全反映系统的实际功率裕度。因为在Hopf分岔点经受小扰动后，负荷节点电压可能就已经出现了周期或非周期振荡。如图6所示，在图4点7和点8处负荷节点电压发生幅值不等的周期振荡；在点9和点10处负荷节点电压发生非周期性振荡失稳。表1给出了相应的分岔参数值（表中功率、电压皆为标幺值），可以看出在图4点4、8、9处励磁电压已经大于5 p.u.，显然不符合电力系统的实际运行情况。

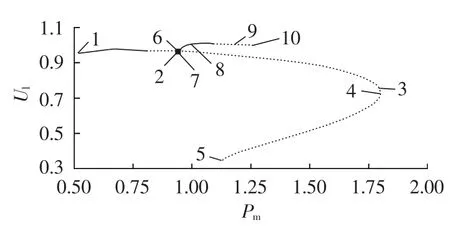
图4 不计励磁饱和环节时的分岔图1Fig.4 Bifurcation diagram 1 excluding excitation saturation element

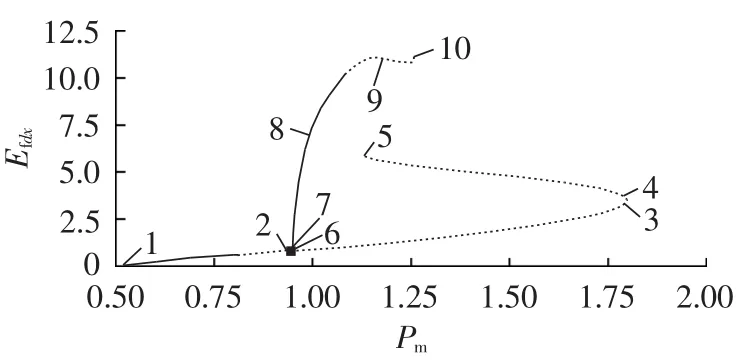
图5 不计励磁饱和环节时的分岔图2Fig.5 Bifurcation diagram 2 excluding excitation saturation element

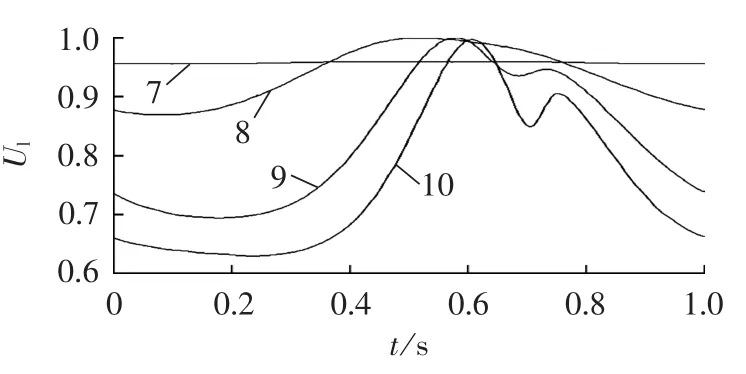
图6 图4中点 7、8、9、10 处的 Ul-t曲线Fig.6 Ul-t curve of point 7，8，9 and 10 in fig.4

表1 不计励磁饱和环节时的分岔参数值Table 1 Bifurcation parameter values excluding excitation saturation element

在实际运行的系统中，发电机励磁电压受到物理结构的限制被约束在特定的范围内，这一范围体现为励磁饱和环节，其具有典型的非线性特征。如果励磁电压达到顶值，饱和环节发生作用，励磁电压为常数，此时电力系统遭受扰动，发电机将失去电压调节能力，导致控制性能下降，系统可能失稳。下面分析励磁饱和环节及励磁电压顶值对系统电压稳定的影响。

2.2 考虑励磁饱和环节时的分岔分析

根据选取模型不同，励磁顶值的取值也不同。文献[25-28]中对的典型取值分别为 1.7、2.3、4.5、5.4和5 p.u.。因此本文简化励磁顶值的取值分别为5、4、3 p.u.。

2.2.1 励磁顶值等于5 p.u.时的分岔分析

当考虑励磁饱和环节且励磁顶值等于5 p.u.时，以图7中的点1（对应图4中的点3）为初始平衡点进行分岔计算。通过与图4的对比可知，考虑励磁饱和环节后负荷节点电压Ul的运动轨迹发生了明显变化，鞍结分岔点推迟出现，并且在机械输入功率等于2.15 p.u.处出现了Hopf分岔，在此分岔点附近出现的非周期性振荡如图8所示。图8中各负荷节点的电压振荡幅值如表2所示。

2.2.2 励磁顶值等于4 p.u.时的分岔分析

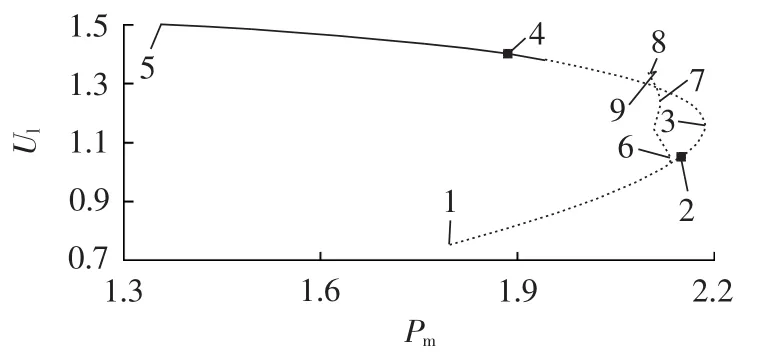
图7 励磁顶值等于5 p.u.时的分岔图Fig.7 Bifurcation diagram when excitation top value is 5 p.u.

当考虑励磁饱和环节且励磁顶值等于4 p.u.时，以点1（即励磁电压刚达到顶值4 p.u.）为初始平衡点进行分岔计算，所得结果如图9所示，同图7比较可知，当系统运行达到励磁极限并在极限上运行时，更小的励磁顶值将使得负荷母线电压随机械输入功率增加更快速地到达鞍结和Hopf分岔点。随着励磁顶值的减小，相应的鞍结分岔点对应的系统功率传输极限也将减小，使系统容易失去稳定。同图10与图8相比可知，在Hopf分岔点附近的小扰动将导致负荷节点电压振荡，随着励磁顶值的减小，振荡幅值明显降低。表3给出了相应的分岔参数值。

图8 图7中点 6、7、8处的 Ul-t曲线Fig.8 Ul-t curve of point 6，7 and 8 in fig.7

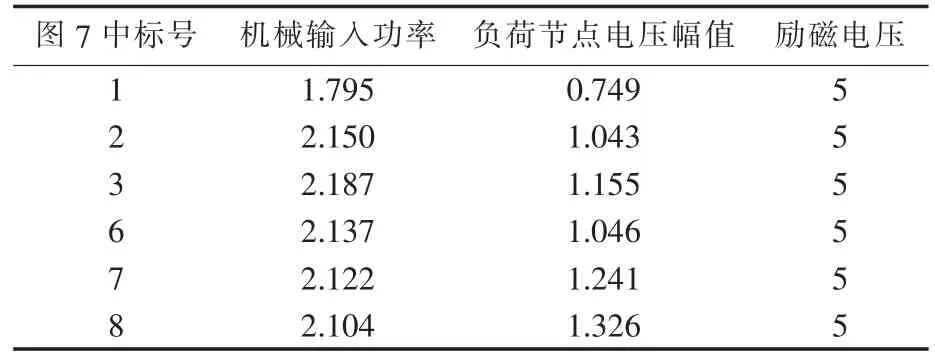
表2 励磁顶值等于5 p.u.时的分岔参数值Table 2 Bifurcation parameter values when excitation top value is 5 p.u.

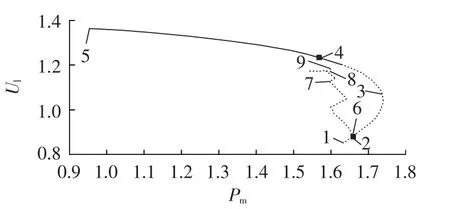
图9 励磁顶值等于4 p.u.时的分岔图Fig.9 Bifurcation diagram when excitation top value is 4 p.u.

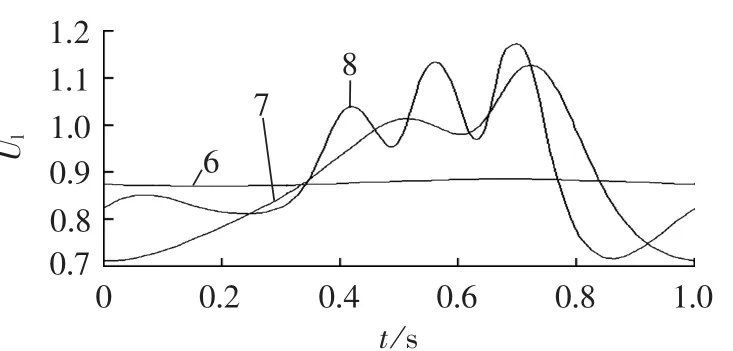
图10 图9中点6、7、8处的Ul-t曲线Fig.10 Ul-t curve of point 6，7 and 8 in fig.9

2.2.3 励磁顶值等于3 p.u.时的分岔分析

当考虑励磁饱和环节且励磁顶值等于3 p.u.时，以点1（即励磁电压刚达到顶值3 p.u.）为初始平衡点进行分岔计算，所得结果如图11所示。同图7比较可知，鞍结分岔点出现之前没有出现Hopf分岔点。随励磁顶值的减小，相应的鞍结分岔点对应的系统功率传输极限将进一步减小，使得系统更容易失去稳定。表4给出了相应的分岔参数值。

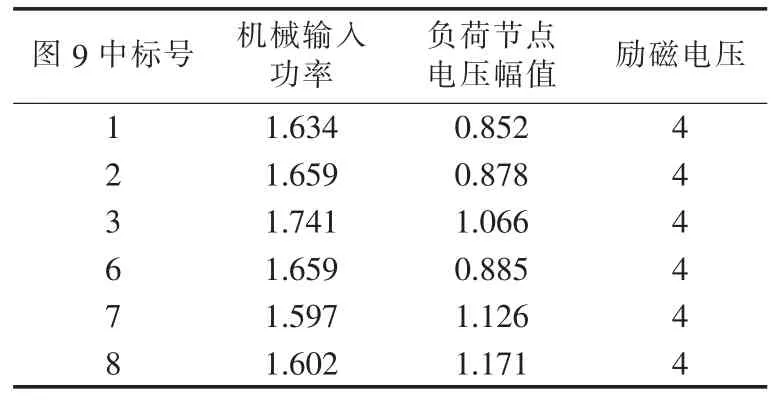
表3 励磁顶值等于4 p.u.时的分岔参数值Table 3 Bifurcation parameter values when excitation top value is 4 p.u.

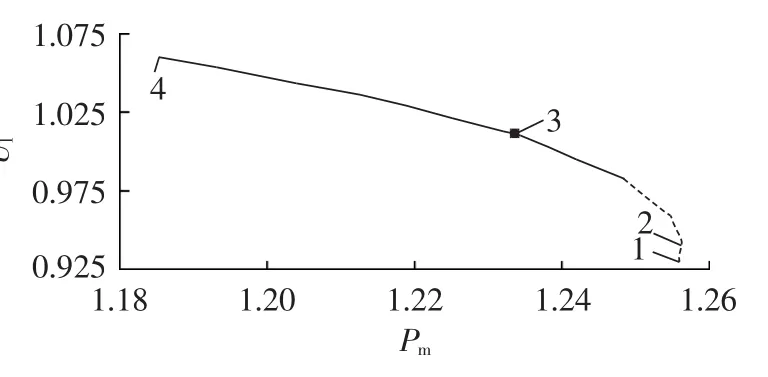
图11 励磁顶值等于3 p.u.时的分岔图Fig.11 Bifurcation diagram when excitation top value is 3 p.u.

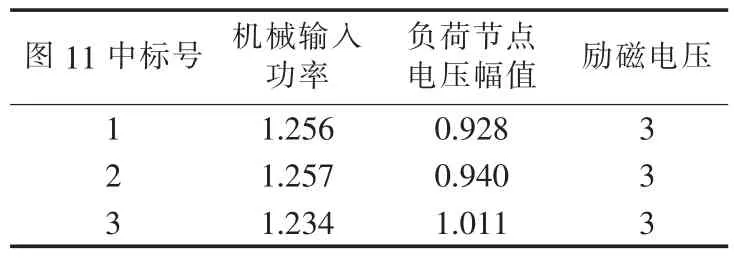
表4 励磁顶值等于3 p.u.时的分岔参数值Table 4 Bifurcation parameter values when excitation top value is 3 p.u.

3 结语

本文以一个3节点电力系统模型为基础，采用感应电动机动态行为的Walve综合负荷模型，研究了励磁饱和环节及励磁电压顶值对系统电压稳定的影响。研究结果表明：随机械输入功率的增加，考虑励磁饱和环节后，负荷节点电压Ul的运动轨迹将发生明显变化。对比励磁电压顶值分别等于5、4、3 p.u.时的分岔分析结果表明：当系统运行达到励磁极限并在极限上运行时，励磁顶值的降低，将使负荷母线电压随机械输入功率的增加以更快的速度逼近鞍结和Hopf分岔点，此时系统稳定裕度的降低使系统更容易失去稳定。对比分岔图4、7、9、11可知，虽然鞍结分岔和Hopf分岔是系统电压失稳的2种表现形式，但励磁饱和环节对它们的影响具有相对一致性。