基于负荷-光伏等效负荷曲线动态分段的配电线路联络开关优化配置

陈 禹，唐 巍，陈昕玥，丛鹏伟，张 璐

（中国农业大学 信息与电气工程学院，北京 100083）

0 引言

联络开关在配电线路中主要起到两方面的作用[1]：连接在多电源线路之间的联络开关的主要任务是实现负荷的转供，提高系统可靠性；连接在单电源线路主干线与分支线间的联络开关的主要任务是进行网络重构，实现经济运行。优化配置联络开关对于保证配电线路经济、安全运行具有重要意义，也符合配电自动化DA（Distribution Automation）的技术需求[2]。近几年，世界光伏发电市场发展迅速，光伏发电正逐渐成为占主导地位的分布式电源[3-4]。光伏发电的合理并网既可以削减重载负荷、减少线路损耗，又符合未来智能配电网的发展目标[5-6]。但是光伏电源的功率输出具有时序性和随机性，传统的开关配置方法不能完全适用于光伏电源并网的情况，因而含光伏的联络开关优化配置具有较高的研究价值。

目前对开关配置的研究有了一些成果。文献[7-8]以优化配置分段开关、断路器和熔断器为研究内容，建立了含开关投资、维护费用和用户停电损失费用的目标函数，寻求开关投资与系统可靠性的平衡；文献[9]对中压配电网环网中的联络开关和分段开关进行优化配置，其综合费用计及了网络损耗费用；文献[10]对含分布式电源DG（Distributed Generation）的配电线路，以开关投资、维护费用、用户停电损失为目标函数进行分段开关的最优配置。目前对配电线路开关配置的研究存在以下不足：

a.光伏电源的并网运行日益增多，且光伏出力具有时序性和随机性特点，因此含光伏配电线路的开关配置方法有其独特性，但是目前对含光伏发电的配电线路开关优化配置的研究较少，特别是针对含光伏发电的配电线路中的联络开关配置的研究尚未见报道；

b.联络开关不仅配置在多条线路之间，在单电源线路内部的主馈线与分支线之间也常配置有联络开关，主要起到在运行阶段调整运行方式的作用，而现有文献对这类联络开关的配置研究很少；

c.负荷在一天中是不断变化的，考虑到日后重构的需要，联络开关的配置应考虑负荷的不确定性，当前开关配置研究还未涉及此方面。

负荷不确定性的处理方法大多是将负荷曲线分段等值，并认为段内负荷为定值。负荷曲线分段目前主要有两大类方法：一是基于模糊聚类的分段方法；二是基于曲线单调性的分段方法。文献[11]采用第一类方法，将负荷数据分类后再以时序性还原；文献[12]采用第二类方法，先按单调性初步分段，然后采用融合思想使分段满足设备动作次数约束。第一类方法会导致分段数过多，不能满足开关动作次数的约束，而且分段数不确定；第二类方法则可根据需要得到相应的分段数，而且直观、计算速度快，不足之处在于无法计及短时激增负荷、曲线首尾相接时刻开关动作判定等日前规划须考虑的具体问题。

综上，针对含光伏的配电线路联络开关优化配置问题，本文建立了负荷-光伏等效负荷曲线并提出动态分段策略，以经济性、可靠性为目标建立多目标数学模型，并分季节、分时段求解，求解算法考虑光伏发电出力的随机性，依据不同的天气情况分别计算目标，并依据每种天气出现的概率确定期望目标，采用IEEE标准算例验证所提出模型和方法的有效性。

1 计及光伏发电和负荷不确定性的配电线路联络开关优化配置思路

光伏电源作为集中式发电的有益补充，可以平衡负荷，减少配电线路的功率损耗[13]，从整体看，光伏发电可以视为“负的负荷”。因此，本文考虑光伏接入对负荷曲线形状的影响，将光伏时序出力曲线与负荷时序曲线进行叠加，形成负荷-光伏等效负荷曲线，对等效负荷曲线进行分段等值，以确定光伏接入情况下的合理分段点。

配电线路联络开关配置方案需适应变化的负荷。依据波动大小将等效负荷曲线分段并认为每一分段内负荷、开关状态均保持不变，是一种可行的简化处理方法。若等效负荷曲线分段过多，不但会因开关频繁操作而使约束条件不能满足，也会因模型计算量较大而难以获得最优解；若等效负荷曲线分段过少，会出现段内的等值负荷与该时段内各时刻负荷有较大偏移，造成优化效果不佳，所以等效负荷曲线分段对开关配置模型求解有较大影响，等效负荷曲线分段与开关配置模型求解应互相协调。本文提出的计及光伏发电的配电线路联络开关优化配置流程如图1所示。

图1 配电线路联络开关优化配置流程图Fig.1 Flowchart of tie switch allocation optimization for distribution line

2 负荷-光伏等效负荷曲线的生成

光伏发电系统的核心器件是太阳能电池板，其输出功率主要取决于电池板上能接收到的太阳光辐射强度，而光辐射强度受天气直接影响[14]。天气分为晴天、阴天、雨天3种情况，认为某种天气条件下光伏电源的出力可由一个二次函数表示[15]：

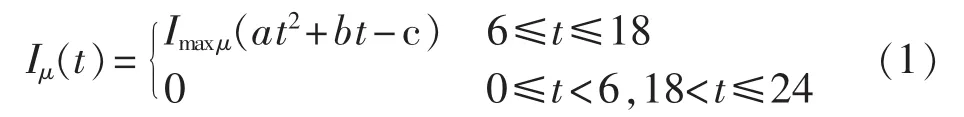
其中，μ 为不同天气状况的状态变量；Iμ（t）为天气状态μ下的光伏时序出力；t为一天中的整点时刻；Imaxμ为天气状态μ下的最大日辐射强度。

光辐射强度还受季节的影响，从规划层面而言，需要给出每一个季节的典型光伏出力，兼顾季节中可能出现的各类天气，典型光伏出力的计算公式如下：

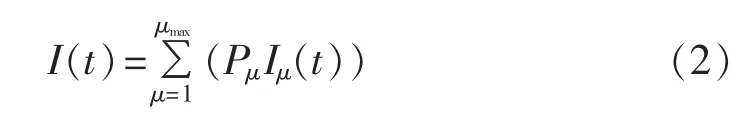
其中，μmax为天气状态的总数；Pμ为天气状态μ出现的概率，可根据该季节各种天气情况出现的天数确定。

负荷曲线与季节也呈现相关性，因此应基于四季的典型负荷计算数学模型[16]，若以所有时刻的负荷采样值计算模型，则计算量十分庞大。为了提高计算速度，需对负荷曲线进行分段等值，认为每一段的负荷波动较小，近似相等。而光伏的接入在一定程度上改变了原始负荷曲线的形状，因此，本文将各种天气下的光伏出力分别与对应的负荷值叠加，形成等效负荷曲线。

下面以春季为例进行等效负荷曲线合成方法说明：设晴天、阴天和雨天在春季的出现概率分别为0.6、0.3和0.1，线路渗透率20%。已知晴天、阴天和雨天的出力曲线，利用式（2）获得典型光伏出力曲线，如图2所示（图中纵轴为标幺值）。图2中的4条曲线分别与配电线路的总负荷叠加，可获得等效负荷曲线，由于光伏电源受太阳光辐射影响显著，本文仅截取06∶00至18∶00的等效负荷曲线，如图3所示。由图3可知：光伏电源在不同的天气条件下对整体负荷水平有一定影响，应对等效负荷曲线进行分段等值；从规划的角度，等效负荷曲线的分段应兼顾光伏电源在不同天气条件下的影响。因此本文对光伏发电典型出力下的等效负荷曲线进行分段，仅以此确定联络开关倒闸操作的时间点。目标函数则需按照各时段的不同天气情况分别计算。

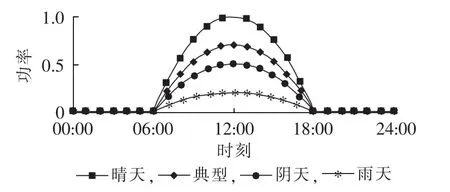
图2 不同天气条件下，光伏发电出力曲线Fig.2 Power output curve of PV source for different weathers

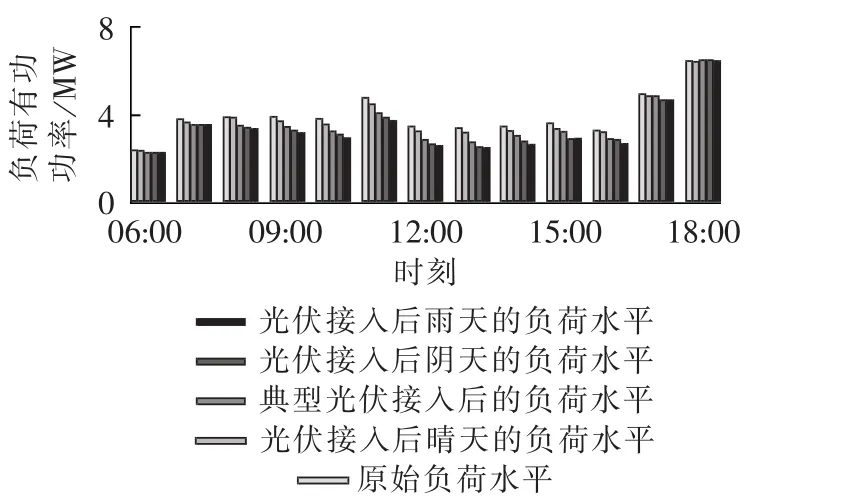
图3 等效负荷曲线Fig.3 Equivalent load-PV curve

3 等效负荷曲线初始分段策略

本文对单调性分段方法做出如下改进。

a.以等效负荷曲线单调区间的积分中值所对应的时刻为分段点进行分段，相比以极值点为分段点的方法段内偏差更小。

b.对负荷短时激增的可能情况，进行了隔离处理。

c.联络开关的配置属规划问题，应考虑每天的开关操作。因此分段策略需要考虑曲线的首尾关联问题，避免每日00∶00时刻不必要的开关动作。

一般根据经验给定等效负荷曲线初始分段数KS，各季节等效负荷曲线的初始分段策略步骤如下。

Step 1：根据单调区间的积分中值进行分段。记曲线各单调区间的积分中值对应的时间坐标为分段点，此时的时段数记为Num。

Step 2：隔离负荷激增时区。采用相邻整时负荷差的绝对值 Ka（a=1，2，…，23）表示负荷变化率，变化率上限值为Kmax。若曲线在某时刻有极大值且其两侧曲线变化率越限，则认为该极值负荷点激增并将其隔离。所有时段的等值负荷均为段内平均值，记为 LPi（i=1，2，3，…），判定此时的 Num是否大于 KS。如果是，则转Step 3，进一步融合已划分的段；否则转Step 4。

Step 3：相邻时段的融合。Step 2中已得到系统的段内等值有功负荷LPi，则相邻时段i和i-1的等值负荷变化量的绝对值为：

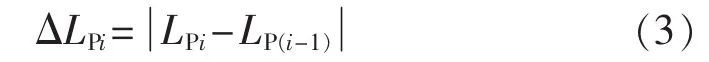
找到最小的ΔLPi，将对应的时段i和i-1合并成一个时段并记为i-1，i+1及其以后全部减1，记Num=Num-1。合并后的等值负荷按下式计算：

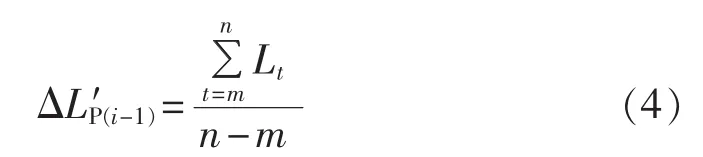
其中，m为时段i-1的起始时间；n为时段i的结束时间；Lt为t时刻对应的负荷值。若此时Num>KS，则重复融合过程，直到Num=KS时转Step 4。

Step 4：处理曲线首尾关联。若首尾时段负荷水平差异不大而分别计算，会造成在00∶00时进行运行方式调整的错误决策。因此，引入统计学中的相对偏差的计算公式，求取曲线最后时段的段内最大相对偏差ΔPmax。将曲线首时段段内负荷依次划进末时段，并求取与末时段的相对偏差ΔPx，直至ΔPx>ΔPmax，停止融合。若首时段完全并入末时段，则记Num=Num-1。融合判定公式如下：

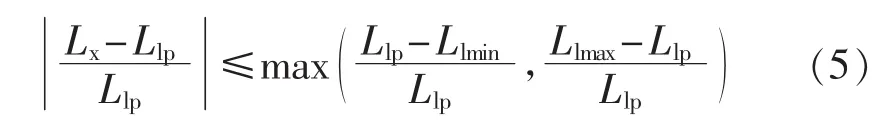
其中，Llp为曲线最后时段的等值负荷（kW）；Lx为首时段各整点负荷（kW）；Llmin为最后时段中的最小负荷（kW）；Llmax为最后时段中的最大负荷（kW）。

Step 5：将Num赋值给KS，输出各分段点对应的时间坐标以及实际分段数KS。

4 联络开关优化配置数学模型及求解方法

4.1 联络开关优化配置数学模型

联络开关一方面可以通过改变线路拓扑来减少线损；另一方面，在故障发生时可以转供负荷，减少停电损失。基于联络开关两方面的主要作用以及第3节得到的分段方案，本文考虑光伏发电的随机性，分别以晴天、阴天和雨天的等效负荷计算各时段损耗电量和停电电量，以损耗电量减少量以及停电损失减少量的期望按时段和季节叠加作为优化目标：

其中，f1为配电线路年损耗电量的减少量；f2为年停电损失费用的减少量；ω1、ω2分别为 f1、f2所占权重。

配电线路年损耗电量的减少量为：

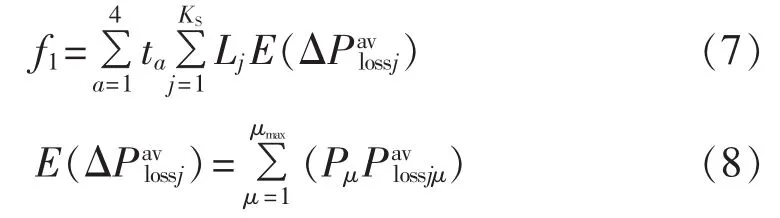
其中，ta为季节a的总天数；KS为等效负荷曲线分段后得到的时段总数；Lj为时段 j的时长；E（ΔPavlossj）为与不考虑光伏接入的初始网络相比，时段j损耗电量减少量的期望值；Pμ为天气状态μ出现的概率，同样根据各种天气情况出现的天数确定；Pavlossjμ为在时段j天气为μ时，与不考虑光伏接入的初始网络相比，平均线损的减少量，可通过时段j光伏的平均功率以及平均负荷求得。

年停电损失费用的减少量为：

其中，N为配电线路节点总数；E（ΔENSp）为装设联络开关后节点p停电电量减少量的期望值；CLp为节点p的单位停电损失；Pavp为节点p在时段j的平均功率；Tp为节点p的少停电时间。

约束条件考虑各季节每一时段的节点电压、功率平衡、可靠性、网络拓扑约束以及开关动作次数约束和开关投资约束。

a.节点电压约束。

b.功率平衡约束。

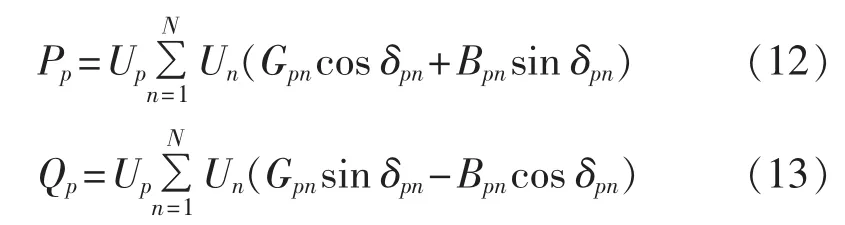
其中，Pp、Qp分别为节点p注入的有功功率和无功功率；Gpn、Bpn、δpn分别为节点 p、n 之间的电导、电纳和电压相角差；Up、Un分别为节点p、n的电压幅值。

c.可靠性约束。

其中，R0为预定达到的可靠性指标。

d.网络拓扑约束。

重构后网络依然为辐射状的连通网络，无孤岛、环网存在。

e.开关允许动作次数约束。

通常，运行部门根据“运行导则”规定[17]，对一天内开关操作次数有相应的限制。

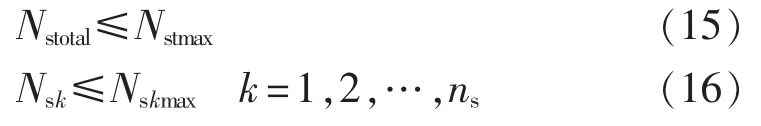
其中，Nstotal为指定时段内联络开关以及分段开关总的操作次数，其上限为Nstmax；Nsk为动作开关集中第k台开关在一天内的动作次数，其上限为Nskmax；ns为参与动作的开关数。

f.开关设备的一次性投资约束。

线路建设的成本有限，需引入联络开关的投资约束限制联络开关的安装台数。

其中，NK为联络开关的安装台数；Cs为联络开关单台投资的现值；Cinv为投资限额。

4.2 模型求解方法

本文采用结合了最小生成树的蚁群优化ACO（Ant Colony Optimization）算法[18]进行求解。 采用生成树策略能保证每一只蚂蚁走过的路径遍历所有节点并且满足辐射状拓扑约束。算法流程如下：

a.设置最大蚁群数量、最大迭代次数及信息素强度；

b.对联络开关候选位置编码，随机选取Nc台候选联络开关加入拓扑信息中，Nc为待安装联络开关个数；

c.开始第g次迭代过程，第k只蚂蚁开始搜索，利用生成树生成可行的辐射状网络，获取开关状态变化向量；

d.对应当前网络进行潮流计算，利用潮流结果计算目标函数；

e.约束条件检验，分别计算节点电压、支路潮流是否越限，若越限则重新生成可行解；

f.记录并保存最优个体，检验蚁群数量是否达到最大，若是则转步骤g，反之则令k=k+1，开始下一只蚂蚁的搜索过程；

g.检验是否满足最大迭代次数，若是则搜索结束，否则随机从候选位置中选取Nc台联络开关加入拓扑信息，令g=g+1，开始下一次迭代计算。

5 等效负荷曲线分段方案的动态修正

应用第3节所得分段点分时段计算目标函数，将开关实际总操作次数Nstotal与规定上限进行比较。若0≤Nstmax-Nstotal<2，表明开关实际动作次数与规定上限之间的裕度不能够满足联络开关配合分段开关进行一次开合操作，则输出目标函数最优解；若Nstmax-Nstotal≥2，即允许开关配合操作至少1次时，对初始分段方案进行如下修正操作。

a.找出现有分段方案中段内负荷差值最大的时段，若其单调，则以该时段中点作为分隔点，记KS=KS+1；若非单调，则采用单调区间融合方法划分，记KS=KS+1。新段内负荷平均值作为其等值负荷。

b.基于新的分段方案再次计算联络开关优化配置模型，得到开关配置方案。

c.再次校验开关动作次数约束，若仍有Nstmax-Nstotal≥2，则再次修正分段方案后进行联络开关优化配置计算，直到Nstmax-Nstotal<2时结束，输出目标函数最优解。

6 算例分析

本文选用IEEE 33节点系统，系统单线图如图4所示。假设各条支路上均装有分段开关，待安装的联络开关投资限额为10万元，联络开关的投资取为2 万元 ／台。 在节点 7、15、23、31 接入 4 台额定功率300 kW的光伏电源，功率因数均为0.85。线路的故障率是0.046次／（a·km），联络开关倒闸操作时间为0.5 h／次，线路修复时间为2 h／次。联络开关候选位置如表1所示。

6.1 计及光伏发电的配电线路联络开关优化配置结果分析

由于各季节的联络开关优化配置步骤相似，因此本节仅以春季为例，详细说明分段方案的动态修正过程。

将蚁群的迭代上限设置为50代。取Nstmax=20，Nskmax=4。根据经验令KS=4，运用第3节Step 1至Step 5所述的初始分段方法得到初始分段方案如图5所示（双向箭头上方的“1”表示时段1，其他类似）。

取ω1=0.7、ω2=0.3，基于初始分段方案求解数学模型，得到春季拟重构方案如表2所示。表2、3中重构时段一列，初始为所有联络开关断开时，Ⅰ—Ⅴ分别对应时段1—5。

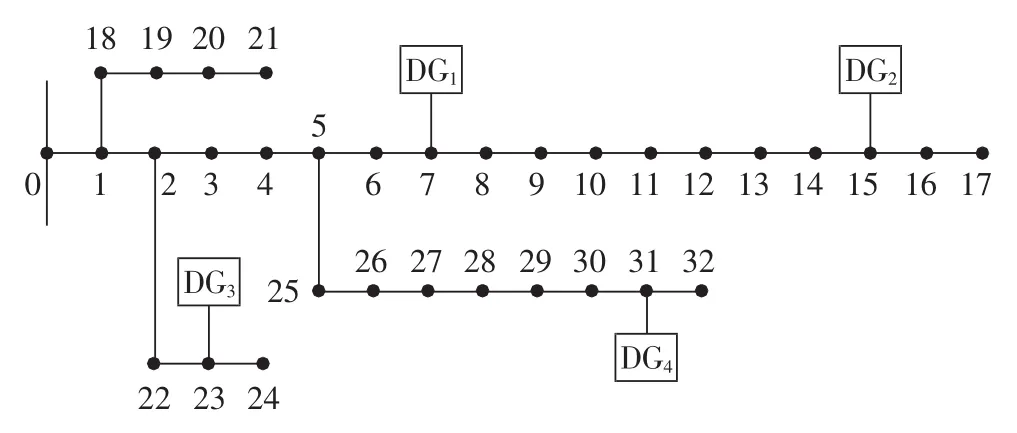
图4 IEEE 33节点系统拓扑图Fig.4 Topology of IEEE 33-bus system

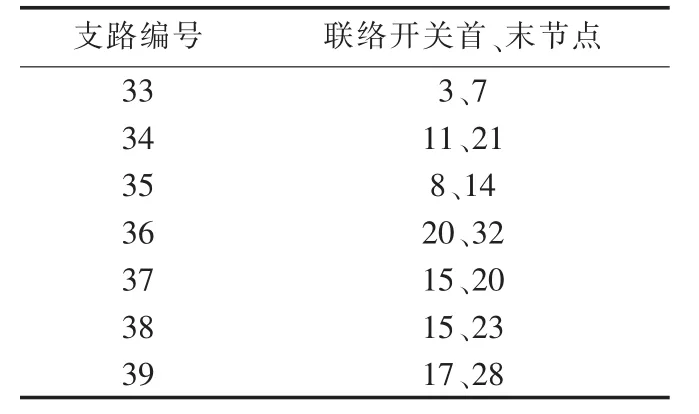
表1 联络开关候选安装位置Table 1 Candidate installation locations of tie switches

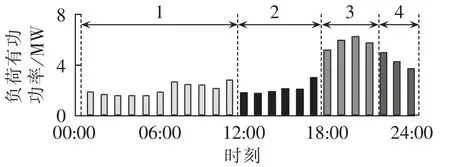
图5 等效负荷曲线初始分段方案Fig.5 Initial segments of equivalent load-PV curve

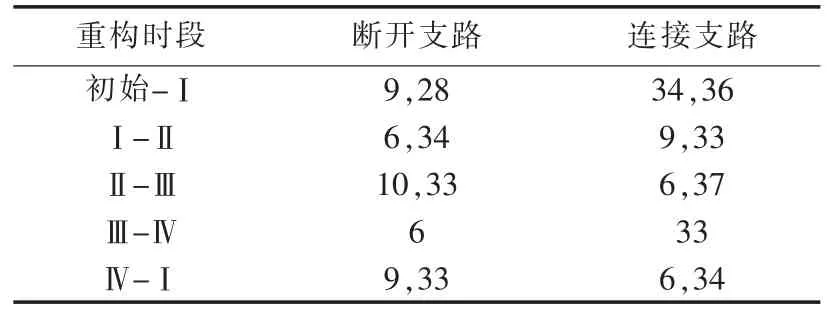
表2 春季初始开关配置方案Table 2 Initial switch allocation scheme for spring

此时Nstmax-Nstotal=20-12=8>2，因此执行动态修正，即基于段内负荷波动修正分段方案。修正后的分段方案如图6所示。合四季的结果，可得联络开关的安装位置如表4所示。

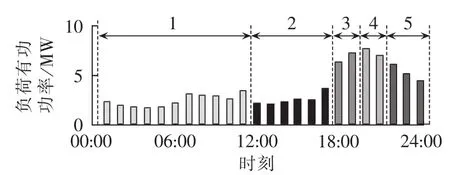
图6 等效负荷曲线修正分段方案Fig.6 Corrected segments of equivalent load-PV curve

基于修正后的等效负荷曲线分段方案求解数学模型，得到春季拟重构方案如表3所示。

此时Nstotal=24>Nstmax，不满足开关动作次数约束，因此选择图5的四分段方案为最终分段方案，同理可得夏、秋、冬季的分段方案以及开关动作方案。综

表3 修正后的春季开关配置方案Table 3 Corrected switch allocation scheme for spring

表4 联络开关安装位置Table 4 Installation locations of tie switches

6.2 各季节负荷-光伏等效负荷曲线分段结果分析

采用与联络开关优化配置数学模型相协调的负荷-光伏等效负荷曲线分段策略，与第6.1节计算过程相似地可得到其他季节等效负荷曲线分段方案如图7—9所示。

图7 夏季（5月）等效负荷曲线分段方案Fig.7 Segments of equivalent load-PV curve for summer（May）

图8 秋季（8月）等效负荷曲线分段方案Fig.8 Segments of equivalent load-PV curve for autumn（August）

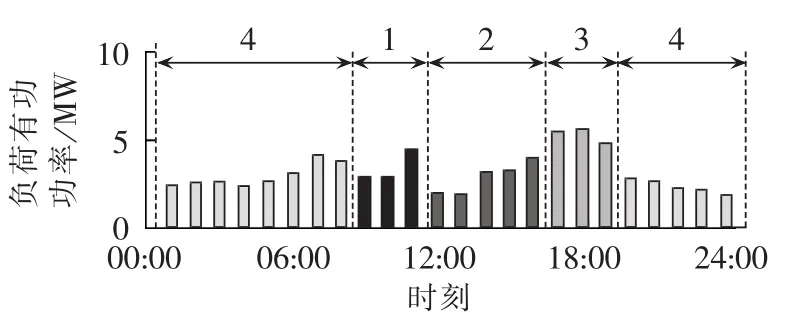
图9 冬季（11月）等效负荷曲线分段方案Fig.9 Segments of equivalent load-PV curve for winter（November）

由图5—9可以得到如下结论：

a.以单调区间的中值点为分隔点相比以极值点为分隔点而言，减小了段内的负荷波动；

b.提出的分段方法考虑到了曲线首尾关联问题，使得分段策略可兼顾配电线路每天的运行方式，符合联络开关配置规划的需要；

c.在开关动作次数的引导下进行时段的动态划分，分段方案以及开关配置方案更加符合工程实际需要。

6.3 联络开关优化配置的结果分析比较

计算计及负荷不确定性和光伏接入的联络开关优化配置多目标数学模型，经统计，得到的结果如表5、表6所示。

表5 各季节优化指标比较Table 5 Comparison of optimization indexes among four seasons

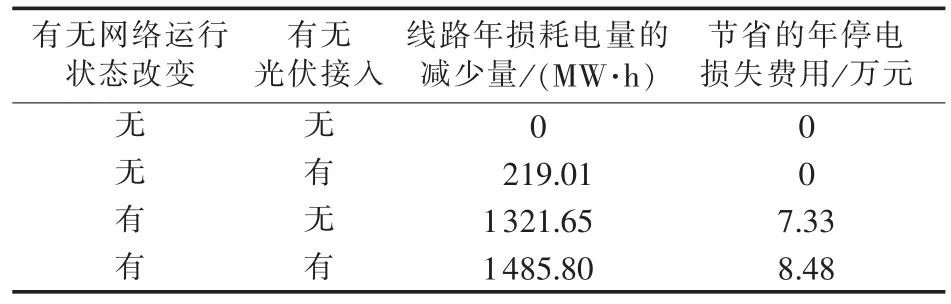
表6 各方案优化结果比较Table 6 Comparison of optimization results among schemes

从表中可以看出：随着季节平均负荷的增减，联络开关在减少线路损耗和提高可靠性方面的贡献也随之增减；光伏的接入可降低线路上的损耗，由于本文采用的光伏发电渗透率较低，因此在降损方面，光伏的作用不及配置联络开关效果明显。但是，未来分布式电源更大规模接入配电线路后，光伏在配电线路运行方面会有更加显著的影响。

7 结论

采用基于负荷-光伏等效负荷曲线动态分段策略，对含光伏电源的配电线路联络开关进行优化配置，采用改进的蚁群算法进行求解，可得到如下结论。

a.在光伏低渗透率情况下，考虑不同季节、不同天气条件的光伏发电特性建立了负荷-光伏等效负荷曲线。基于等效负荷曲线分段获得的联络开关配置方案使计算效率大幅提高，而且相比无光伏发电接入的情况网损电量节约11.05%，停电损失费用节约13.56%。若光伏以高渗透率模式接入线路，其随机性会对负荷曲线形状有较大影响，则不宜通过等效负荷曲线分段来确定开关动作时间，应逐点计算目标函数，以目标函数引导开关动作时间。

b.等效负荷曲线的分段策略考虑了负荷水平、负荷变化率及曲线首尾关联，避免了现有单调性分段方法可能存在的段内负荷波动过大问题，更加符合开关配置的实际需求。

c.将等效负荷曲线的动态分段与数学模型相结合，能够在满足配电线路损耗、可靠性、开关投资及动作次数等约束的条件下，获得适应于不同负荷水平的联络开关配置方案。