近Hermite流形上联络的关系

杨松林

(1.苏州大学数学科学学院，江苏 苏州 215006；2.苏州大学文正学院，江苏 苏州 215006)

实2n维近Hermite流形是具有Hermite度量的近复流形,其上同时具有U(n)结构和SpinC(2n)结构,因此近Hermite流形上有Levi-Civita联络、Hermite联络和SpinC联络.笔者将讨论这3个联络的关系.

1 近Hermite流形与SpinC流形的关系

设M是实2n维近Hermite流形，·,·是流形M的Riemann度量，·,·C是流形M的Hermite度量，J:TM→TM是流形M的近复结构,C2n(-1)[1]是Clifford代数，其生成元为{e1,e2,…,e2n}.

引理1[2]设U(n)是n维酉群,SpinC(2n)是SpinC群,则存在嵌入λ:U(n)→SpinC(2n).

根据引理1，复流形、近Hermite流形与SpinC流形有如下关系:

引理2[3]每一个实2n维复流形和实2n维近复流形都是SpinC(2n)流形.

由引理2可知,实2n维近Hermite流形同时具有U(n)结构和SpinC(2n)结构.

2 近复联络、Hermite联络与SpinC联络

设U(M)是M上的U(n)切主丛，U(M)×μSO(2n)=TM,其中映射

定义1[4]一个联络C称为近复联络,若联络C满足：(1)C保Hermite度量

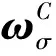
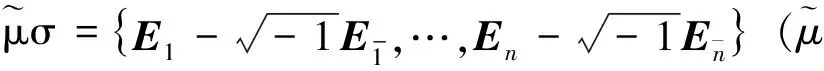
(1)

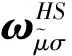
(2)

其中:

ρ1:SpinC(2n)→SO(2n):eiθg0ρ(g0)[4].

ρ:Spin(2n)→SO(2n)[5]是二重覆盖.流形M上SpinC(2n)联络S的联络形式为

(3)

由以上讨论可知,近Hermite流形M上有4个联络，即Levi-Civita联络L、近复联络C、Hermite联络HS和SpinC(2n)联络S.

3 Hermite联络与SpinC(2n)联络的关系

在近Hermite流形M上,有

TM=U(M)×μSO(2n),SpinC(M)=U(M)×λSpinC(2n).

引理1中的嵌入λ:U(n)→SpinC(2n)诱导一个李代数映射

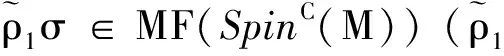
适当选取主丛SpinC(M)的U(1)丛上U(1)联络U，使之满足φ=tr(ω(3)+ω(3)T),这样得到2个联络在局部截面下的差异，

推论1若流形M是Kähler流形，则Hermite联络与SpinC(2n)联络的差异A=O.