相似理论在门式起重机主梁架有限元分析中的应用与研究

李新华，周绪波

（中南林业科技大学 机电工程学院，长沙 410000）

0 引言

相似理论是结构模型试验研究中，指导试验模型建模和求解的理论基础 。将相似理论与有限元的数值模拟仿真技术结合在一起运用到工程分析中已成为一种普遍且实效的路径[1]。

1 相似理论

相似理论经过不断的修改和完善，已是相当成熟，其理论基础被确立相似三定理。

1）相似第一定理：现象彼此相似，两者单值条件相同，则相似准则的数值比值为1[2]。

2）相似第二定理：当任意一个物理现象包含N个物理量，且这些物理量中含有K个基本量，则这N个物理量可以由相似准则π1，…… ，πN-K之间的函数关系来表示。

对于任一现象的物理方程可以表示为：

根据相似第二定理转化为：

3）相似第三定理：彼此现象的单值条件（系统的几何条件、介质物理性质）相似，且由单值条件导出的相似准则在数值上相等，则现象彼此相似[3]。

相似理论应用到模型试验中的重要作用是确定相似现象中各个对应参数的相似比，而求解相似比通常选用量纲分析法。

2 量纲分析法

2.1 基本概念

量纲：表征物理量按其性质不同而划分的类别，即量纲表示的是物理量的种类[4]。

根据国际单位制中的七个基本量的量纲，可以推导出其他常见物理量的量纲，如表1所示。

表1 常见导出物理量的量纲

2.2 量纲分析法的优势

在解决实际问题时，多采用三种求解方法：定律分析法、方程分析法和量纲分析法[5]。

1）定律分析法要求对所研究问题涉及到的多个物理规律有清楚的认识，认清内在联系。所以对于不同的研究人员对于同一问题的认知以及所考虑的重点不同，便会产生不同的结果，方法的可靠性和准确性容易受到外界影响。

2）对于方程分析法来说，能解决的问题的基础是能够得到问题的数学模型，但是对于某些问题而言，其数学模型难以建立或获取，因此方程分析法的局限性显而易见。

3）量纲分析法的理论基础来源于量纲齐次方程的数学理论。通常来讲，用以说明物理现象的方程都是齐次的。同时具有确定的量纲，因此量纲分析法解决实际问题更加方便。具体有关方面的详细介绍和应用可参考文献[6，7]。

上述三种方法，经过对比可以发现，量纲分析的适用性以及适用范围优于另外两种方法。研究同样采用量纲分析法。

以门式起重机[8]为实例，运用量纲分析推导出门式起重机各个参数相似比，根据相似比重新进行建模以及加载，求得的应力等参数与实际进行比较分析，来表明相似理论的应用价值与实际研究。

3 相似理论应用与研究

实例分析对象为株洲天桥起重机股份有限公司生产的32/10t电动双梁门式起重机。起重机由两主梁和两端梁、两挠性支腿和两刚性支腿、小车运行机构和大车运行机构组成。起重机跨度20m，主梁长41.5m，起升高度为15m。有限元仿真平台是数值模拟仿真软件ANSYS Workbench[9]。

3.1 相似常数的求解

根据门式起重机实际工作情况，选取其主要的物理参数，运用相似理论中的相似第二定理，建立物理相似准则：

选取力，长度，时间为相似模型的基础量纲。推导出各物理量的量纲矩阵。

表2 各物理量的量纲矩阵

原型与模型在几何形状上相似，在材料特性和边界条件三个方面完全相同，所以选取材料密度ρ、弹性模量E、构件长度L为基本量纲。因此可以得知Cρ=ρ/ρm=1，CE=E/Em=1，CL=L/Lm=λ，（C表示起重机原型参数与模型参数的相似比，ρ、E 、L、μ表示原型的参数，ρm、Em、Lm、μm表示模型的参数，λ表示模型相对于原型缩小的比例）。

根据上述研究过程中原型与模型参数的已知比例结合相似理论，其余参数的相似常数（相似比）为：

以此推导出起重机原型参数与模型参数的相似比：

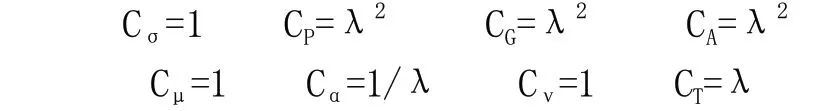
3.2 起重机原型有限元分析

原型与各个相似比的建模软件为NX。分析软件为ANSYS Workbench，分析得出数据汇总到Microsoft Excel，最后结合Origin绘图软件进行曲线绘制。

图1为起重机原型的有限元模型，起重机原型主梁高度1.85m，宽1.2m，全长41.25m。为避免多变量对研究结果的影响，采用单一工况。载荷施加在距离刚性支腿侧端梁20.95m处，考虑重力载荷和起重载荷和风载荷的作用，假定起重载20T。有限元模型都采用Tetrahedrons方式进行网格划分。

图1 起重机原型有限元模型

起重机原型主梁应力分布情况如图2所示。

图2 起重机原型主梁架应力分布图

3.3 各个相似比模型有限元分析

研究共采取五个相似比，从λ=10到λ=30，以等差形式Δλ=5分别建模，导入到ANSYS Workbench分析结果如图3所示。

图3 30倍相似比主梁架应力分布图

图4 25倍相似比主梁架应力分布图

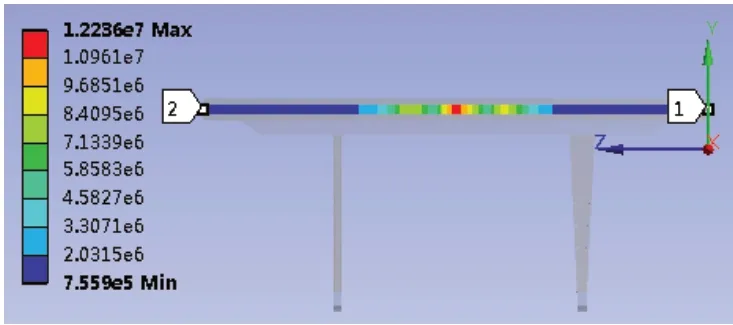
图5 20倍相似比主梁架应力分布图

图6 15倍相似比主梁架应力分布图

通过图2～图7的对比和对收集到的应力数值进行分析，原型和模型在主梁上等效应力的分布规律是一致的。从这一工况来看，危险区域发生在距离刚性支腿侧端梁20.625m处。

图7 10倍相似比主梁架应力分布图

原型有限元分析中生成2867698个节点和1597945个单元。各个相似比模型生成的单元数和节点数明显少于原型，例如30倍相似比的模型生成677860个节点和304581个单元，10倍相似比的模型生成1016545个节点和754655个单元。起重机原型需要在计算机工作站上计算时间超过8个小时，而各个相似比模型只需要在普通个人计算机上计算1～3小时。在得到精准结果的情况下，有限元分析的过程中运用相似理论，大幅度减少了工作量、节约时间和资源。

3.4 相似比与误差规律分析

对于门式起重机在研究和实际工程应用过程中，对于主梁架的校核更加着重局部关键位置而不是全部。对于本文研究对象，根据图8起重机原型主梁架应力曲线，着重考虑图示三个关键位置。

图8 起重机原型主梁架应力曲线

图9 起重机有限元分析研究位置示意图

表3 各个相似比与原型主梁架应力值

表4 各个相似比与原型主梁架应力相对误差值

位置1、位置2、位置3分别距起重机主梁架左侧17.1875m、20.625m、24.922m。分别采取设定的相似比进行建模导入到ANSYS Workbench进行有限元分析，得出各个相似比应力值并求出与原型应力值的相对误差。

1）对于正百分比的数据，根据相似模型得出的数据大于实际原型数据，考虑到校核时都会添加一个安全系数，因此实际运用中根据相似模型的应力数据得出起重机的其他参数更加满足实际的要求。若要在实际应用中得到更加精准的结果，可以根据上图得到误差值还原到原型当中去。例如相似比为10倍时，在起重机主梁架20.625m处（即应力最大处）的误差为4%。实际应用中，根据10倍相似比得到的应力值减小4%即为原型的应力值。

2）对于负百分比的数据，根据相似模型得出的数据小于实际原型的数据。根据上图，三点位置处应力误差可以控制在10%以内，在实际运用中要加以校正。同样若要获取更加精准的结果，可以将应力值还原到原型当中去。

4 结论

1）本文采取多个相似比在有限元分析中引入相似理论，在弥补分析不足，克服其局限性的同时,提高分析效率，节约资源和时间。

2）采用多个相似比建模进行有限元分析，得到应力值数据，与原型的数据汇总。通过对实际工程应用中比较重要的三个位置的应力数据分析，得出各个相似比模型应力值与原型的应力值十分接近，其数值误差满足实际工程要求。

研究过程中相似倍数的选取十分重要，不仅影响模型的大小，同样影响载荷的大小，直接决定结果的准确性。

以λ代表相似倍数，根据相似理论计算，模型所受载荷的大小的相似倍数变为λ2。假设λ取为40，则模型所受力的大小缩小1600倍。

因此相似倍数不能取值较大或者较小，除载荷会发生明显变化外，不利于起重机内部微小结构的建模，同样会对整体结构产生不确定的影响。若是装配模型，也会影响零件之间的装配关系。导入有限元分析软件时也会发生结构上的变化，导致不能求解，影响求解结果的准确性。综合以上考虑，因此在实际工程应用时，优先选取低相似比进行求解。

3）通过对数据的分析，得出较小相似比在满足精度的前提下，具有良好的实际应用价值。同时证实了在大型结构件的有限元分析中，结合相似理论，成为一种新的解决途径。

[1] 李新华,曹伟魏,唐敏.相似理论在大型复杂构件有限元分析中的应用[J].机械设计与研究,2013,29(5)：18-20.

[2] 仵锋锋,曹平,万琳辉.相似理论及其在模拟试验中的应用[J].采矿技术,2007,7(4)：64-65.

[3] 易纲,龚代瑜.试论结构模型设计中的相似理论[J].国外建材科技,2004,25(5)：38-39.

[4] 邵友元.对量纲分析法与π定理的理解与应用[J].东莞理工学院学报,2010,17(3)：106-109.

[5] 胡东奎,王平.相似理论及其在机械工程中的应用[J].现代制造工程,2009,11：9-12.

[6] 徐婕,詹士昌.量纲分析的基础与应用研究[J].科技通报,2004,20(1)：51-54.

[7] 胡云.量纲分析应用性研究[J].大连民族学院学报,2006,34(5)：70-74.

[8] 李新华,唐敏,曹伟魏.龙门起重机主梁有限元分析[J].中南林业科技大学学报,2013,33(5)：111-113.

[9] 叶阜,张宝国,张起伟,等.基于ANSYS Workbench的斗轮堆取料机关键零部件的有限元分析优化[J].起重运输机械,2008,(12)：83-86.