基于VC的逐点比较空间直线插补算法改进与仿真
2015-09-13赵庆志
王 选,赵庆志
(山东理工大学 机械工程学院,淄博 255049)
0 引言
数控机床加工各种形状的零件轮廓时,必须控制刀具相对于工件以给定的速度沿指定的路径运动,这一功能称为插补。绝大多数机床数控系统都具有平面直线和圆弧插补功能,很少具有三维空间插补功能。但在实际生产中,特别是在铣床、镗床等三坐标机床的加工中,经常要求加工空间图形,特别是空间直线,所以经济型数控机床的插补系统应具有空间直线插补等功能。
1 基于基础坐标空间直线插补算法
传统的逐点比较空间直线插补包括偏差判别、坐标进给、新点偏差计算和终点判别4个步骤,该算法在坐标进给时不考虑进给后插补误差的大小而直接决定进给坐标,致使插补误差比较大[1~4]。在前人研究的基础上,引进基础坐标[5]的概念,提出了一种基于基础坐标的逐点比较空间直线插补算法,以实现机床X、Y、Z三轴联动功能且有效地提高了空间直线插补速度与精度。
1.1 三维空间24区域划分
在三维空间中,第一象限划分为三个区域的方法[6]如下:利用过原点O的平面AOE,BOE,COE将第一象限空间为三个正四锥型的区域,即X≥Y、X≥Z区域1,Y>X、Y≥Z区域2,Z>X、Z>Y区域3,如图1所示。这三个平面中AOE垂直平面XOY并且与X轴、Y轴的夹角为45°,BOE垂直平面YOZ并且与Y轴、Z轴的夹角为45°,COE垂直平面XOZ并且与X轴、Z轴的夹角为45°。其他每个象限划分区域方法同第一象限相同,三维空间总共分割为24个区域。

图1 第一象限划分为三个区域
1.2 插补公式推导
如图2(a)所示,设要加工区域1以O(0,0,0)为原点,以E(Xe,Ye,Ze)为终点的OE空间直线段,Xe≥Ye,Xe≥Ze,且Xe,Ye,Ze均为正值,X坐标为基础坐标。
通过文献[7]得知,每次单独进给X坐标、Y坐标或Z坐标叫做基础坐标进给,同时进给两个坐标或三个坐标及以上叫做联合坐标进给。图2(b)中的直线为OE在XOY坐标平面内的投影,当基础坐标+X进给时,得出新偏差值为:

图2 三维空间坐标系

当联合坐标+X、+Y进给时,得出新偏差值为:

空间直线OE在XOZ坐标平面内投影如图2(c)所示,同样当基础坐标+X进给时,得出新偏差值为:

当联合坐标+X、+Z进给时,得出新偏差值为:

有了上述4个平面偏差计算公式,现在关键是如何将其运用到空间直线的偏差判别和计算,以决定下一步进给的走向。下面规定:
1)若|Fy|>|Fxy|,|Fz|>|Fxz|,则沿X轴、Y轴和Z轴方向进给脉冲,令Fxy值赋给Fv,Fxz值赋给Fz;
2)若|Fy|>|Fxy|,|Fz|≤|Fxz|,则沿X轴和Y轴方向进给脉冲,令Fxy值赋给Fy,Fz值赋给Fxz;
3)若|Fy|≤|Fxy|,|Fz|>|Fxz,则沿X轴和Z轴方向进给脉冲,令Fy值赋给Fxy,Fxy的值赋给Fz;
4)若|Fy|≤|Fxy|,|Fz|≤|Fxz|,则沿X轴方向进给脉冲,令Fy值赋给Fxy,Fz值赋给Fxz。
以上规定适用于xe≥ye且xe≥ze区域,三维空间插补偏差判别与计算如表1所示。
2 改进后空间直线插程序设计
空间直线插补程序设计的基本思想是:程序开始时,根据向量的坐标运算法[8]判断空间直线所在的象限,然后根据基础坐标判别进入各自的区域进行插补运算,最后进行判终处理及返回到相应的象限。空间直线插补程序中直线所在象限判别与基础坐标判别方法比较简单。下面对空间直线插补过程[9]进行详细介绍,以第一象限区域1为例,X为基础坐标,初始插补偏差均为0。插补流程图如图3所示,其他区域与此相似。
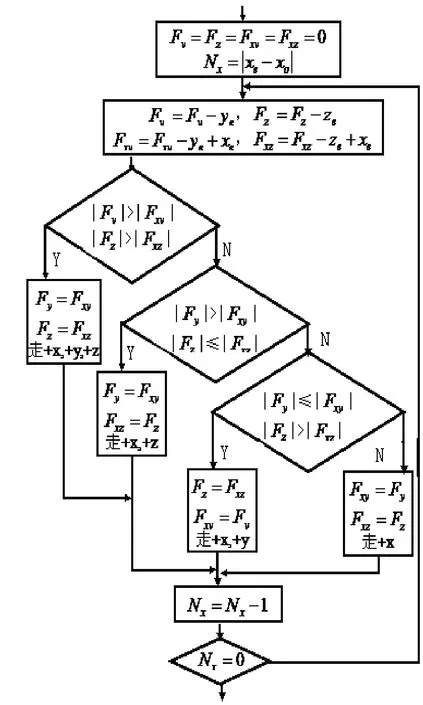
图3 区域1插补流程
VC++6.0软件采用面向对象的机理设计程序,适用于开发各类应用系统。现在以VC++6.0软件为程序开发平台,对空间直线插补进行仿真[10]。
界面设计如图4所示。绘图区域尺寸为300×300,操作者可以在编辑框中设置直线坐标和步长的任意大小,单击绘制空间直线等按钮可实现相应功能。
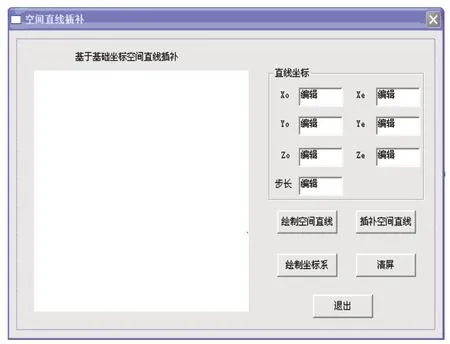
图4 界面设计
VC++6.0软件设计程序需要大量映射函数,下面介绍实现各功能的函数。
void CBaseLineDlg::OnBtnDrawzuobiao(),该函数实现绘制空间坐标系功能。
void CBaseLineDlg::OnBtnDrawline(),该函数实现绘制空间直线功能。因为空间直线有X、Y、Z三个坐标值,但是该空间直线在VC++中要以二维平面的形式绘制出来,所以设计编写程序时运用到正等轴侧变换矩阵T=[0.7071,0,-0.4082,0;-0.7071,0,-0.4082,0;0,0,0.8165,0;0,0,0,1]。插补过程程序也运用正等轴测变换矩阵,下文不再详述。
void CBaseLineDlg::OnBtnClear(),该函数实现清屏功能。
void CBaseLineDlg::OnBtnClose(),该函数实现退出功能。
void CBaseLineDlg::OnBtnChabuline()
{ UpdateData();
if(m_originx==m_endx && m_originy==m_endy
&& m_originz==m_endz)
AfxMessageBox(“请输入坐标不同的两点!”);
if(m_step==0)
AfxMessageBox(“请输入插补步长!”);
//判断空间直线所在象限
chax=m_endx-m_originx;
chay=m_endy-m_originy;
chaz=m_endz-m_originz;
if(chax>=0)
{ if(chay>=0)
{if(chaz>=0) Chabu1();
else Chabu5();}
else
{if(chaz>=0) Chabu2();
Else Chabu6();}}
else
{if(chay>=0)
{if(chaz>=0) Chabu4();
else Chabu8();}
else
{if(chaz>=0) Chabu3();
else Chabu7();}}}
该函数实现判别空间直线所在象限的功能,插补过程功能需调用Chabu1()等函数。
void CBaseLineDlg::Chabu1()
{//定义插补过程中变量
float drawx,drawy;
float Fx,Fy,Fz,Fxy,Fxz,Fyx,Fyz,Fzx,Fzy;
int Nx,Ny,Nz;
//运用正等轴侧变换矩阵求得X、Y绘制坐标
drawx=7.071*m_originx-7.071*m_originy;
drawy=-4.082*m_originx-4.082*m_originy
+8.165*m_originz;
pDC->MoveTo(drawx,drawy);
//第一象限X坐标为基础坐标
if(abs(chax)>=abs(chay) &&
abs(chax)>=abs(chaz))
{ Fy=0;Fz=0;Fxy=0;Fxz=0;Nx=abs(chax);
while(Nx>=m_step)
{Fy=Fy-abs(chay)*m_step;
Fz=Fz-abs(chaz)*m_step;
Fxy=Fxy-(abs(chay)-abs(chax))*m_step;
Fxz=Fxz-(abs(chaz)-abs(chax))*m_step;
if(abs(Fxy)<=abs(Fy) && abs(Fxz)<=abs(Fz))
{ Fy=Fxy; Fz=Fxz;
m_originx=m_originx+m_step;
m_originy=m_originy+m_step;
m_originz=m_originz+m_step;}
else if(abs(Fxy)<=abs(Fy) &&abs(Fxz)>abs(Fz))
{ Fy=Fxy;Fxz=Fz;
m_originx=m_originx+m_step;
m_originy=m_originy+m_step;}
else if(abs(Fxy)>abs(Fy) &&abs(Fxz)>abs(Fz))
{ Fxy=Fy;Fxz=Fz;
m_originx=m_originx+m_step;}
else
{ Fxy=Fy;Fz=Fxz;
m_originx=m_originx+m_step;
m_originz=m_originz+m_step; }
drawx=7.071*m_originx-7.071*m_originy;
drawy=-4.082*m_originx-4.082*m_originy
+8.165*m_originz;
pDC->LineTo(drawx,drawy);
Nx=Nx-m_step;Sleep(100);}
//第一象限Y坐标为基础坐标和第一象限Z坐标为//基础坐标插补程序省略}
3 改进后空间直线插补实例与仿真
现加工区域1内以坐标原点O(0,0,0),E(6,5,3)为终点的空间直线段OE。利用改进后的插补算法进行插补计算如表2所示。
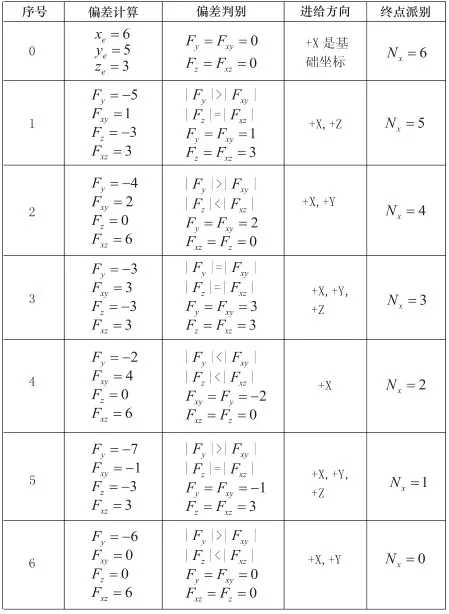
表2 空间直线插补过程
通过上述实例数据可以看出:优化后的逐点比较法空间直线插补的总步长插补次数为6,大大提高了插补速度;优化后的逐点比较法空间直线插补的最大偏差|F|=3,有效地提高了插补精度。
为了验证上述算法的正确性,利用VC++6.0软件编写插补程序源代码,模拟仿真空间直线插补过程,以实现空间直线插补功能如图5所示。
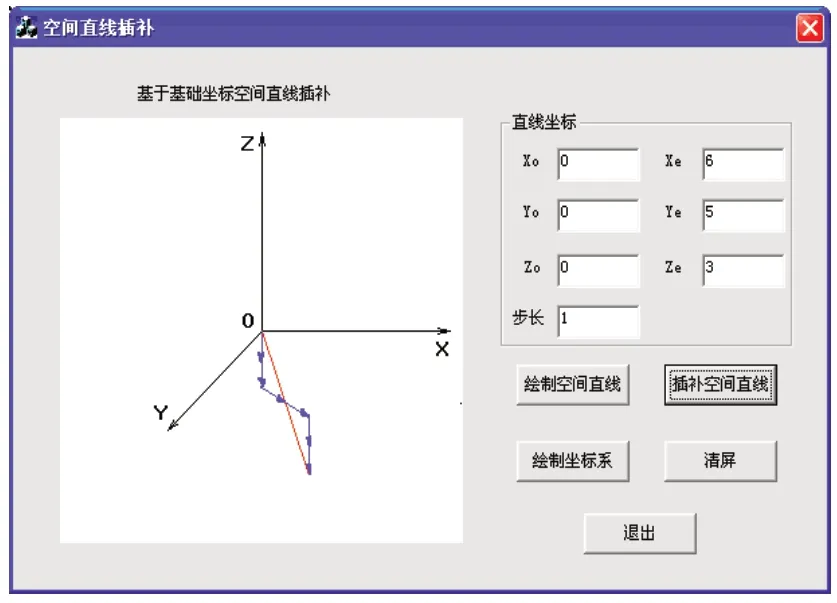
图5 插补实例仿真
4 结束语
基于基础坐标概念的逐点比较空间直线插补方法运用了新的插补公式,插补思路更加清晰,插补信息清晰明了;该方法中避免了有关文献所述方法中涉及的导数计算、有可能出现斜率无穷大、计算麻烦等缺点;空间直线的插补步数等于其基础坐标的绝对值,终点判别一目了然且提高了插补速度;插补过程中的最大偏差大大减小了,有效地提高了逐点比较空间直线插补精度。该算法可以实现串联机床三轴联动、六轴并联机床六轴联动功能,进一步提高了数控系统的插补速度,有效地提高了逐点比较空间直线插补精度和刀具半径补偿精度。
[1] 席港港,赵庆志,王军,田晓文.传统逐点比较法直线插补方法的改进[J].山东理工大学学报,2012,(1):67-69.
[2] 李占斌,万长庆.实现数控机床三轴联动的逐点比较法[J].机床与液压,2004,(7):64-65,22.
[3] 高有行.对逐点比较法的改进算法[J].西安电子科技大学学报,1998,25(3):299-303.
[4] 范希营,郭永环.提高数控系统基准脉冲直线插补速度及精度的研究[J].制造技术与机床,2010,(3):89-91.
[5] 王敏.差分插补方法及其在数控线切割机中的应用(一)[J].电加工与模具,1981,(4):16-22.
[6] 赵庆志,席港港.基于基础坐标概念的逐点比较法圆弧插补原理及其应用[J].制造业自动化,2012,34(21):69-71,84.
[7] 逄启寿,冯羽生.基于C语言的数控直线逐点比较法的程序实现[J].制造业自动化,2009,31(6):54-56.
[8] 聂建成,吴竹溪,肖洁,吴铁军.基于直线插补的进给方向判断新算法[J].组合机床与自动化加工技术,2009,(10):12-14.
[9] 叶秀云,朱文,田刚.一种简捷的快速直线插补新算法[J].组合机床与自动化加工技术,2005,(7):28-30.
[10] 杨代华,陈志辉.基于实时操作系统μC/OS—II的数控系统研制[J].制造技术与机床,2007,(12):20-23.
