数控系统数字积分法插补原理研究与仿真
2015-09-13汪木兰
刘 萍,汪木兰,赵 超
(1.宿迁学院,宿迁 223800;2.南京工程学院 先进数控技术江苏省高校重点建设实验室,南京 211167;3.江苏省电力公司宿迁供电公司,宿迁 223800)
0 引言
插补模块是整个数控系统的一个及其重要的功能模块,插补的速度和精度直接影响到数控系统的精度、速度和加工能力等内容[1~4],而插补的实质是数据点的密化,即在已知的刀具轨迹转接点间插入若干中间点的过程,中间点的获取可根据相应的算法由数控系统软件或硬件来实现,以此来协调控制各坐标轴的运动,从而获得所需要的运动轨迹。常用的插补算法有:脉冲增量插补和数据采样插补,而脉冲增量插补中最常用的是逐点比较法和数字积分法。由于逐点比较法插补不能实现两轴联动,数字积分法可以实现两轴联动,本文将对脉冲增量插补中的数字积分法进行论述并对轨迹和插补过程进行仿真研究。
1 数字积分法插补原理
利用数字积分的原理进行插补计算的方法,称为数字积分法,也称为DDA法。数字积分法的优点在于容易实现多轴联动插补,可以描述空间直线和平面各种函数曲线。
1.1 DDA直线插补
1)原理:利用各坐标轴的速度分量进行数字积分来确定刀具在各坐标轴上的位置,设刀具进给速度为V,在X轴、Y轴的进给速度分量分别为VX、VY,则 tΔ时间内的位移量为:

由图1的几何关系得出:

图1 DDA直线插补

则位移量:

当刀具由O点切削到E点时,tΔ经过0→t的积分,位移公式可表示为:

设寄存器的位数为N位(容量为2N),n为累加次数(整数),取n=2N,经过n次累加后,到达终点,则kn=1,k=1/n=1/2N。当tΔ取为1时,则:

2)特点:在DDA直线插补中,取两个函数寄存器JVX、JVY,分别存放终点坐标Xe、Ye,均为定值;再取两个余数寄存器JRX、JRY;终点寄存器J∑(J∑=2N)。当X轴、Y轴积分器中的值超过2N-1时,便发生溢出,溢出时的余数存放在JRX、JRY中,每溢出一次,J∑自动减1,经过2N次累加后,溢出脉冲的总数等于被积函数值。
1.2 DDA圆弧插补
1)原理:以第一象限顺时针圆弧SE为例,如图2所示。
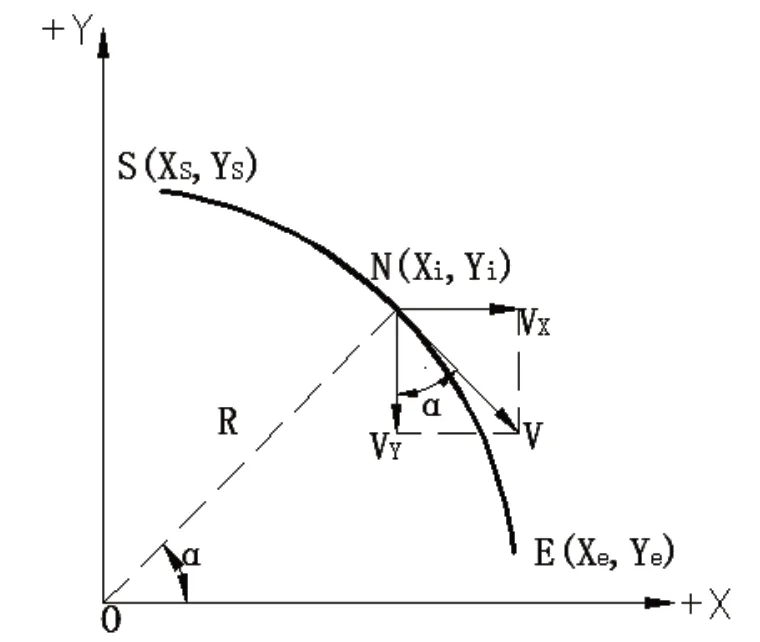
图2 DDA圆弧插补

将方向矢量代入计算公式,则第一象限顺时针圆弧的速度计算公式为:

Δt时间内,位移增量为:

当Δt为1,K=1/2N时,则:

由计算公式可看出,圆弧插补时,积分器是对动点Xi、Yi进行累加。插补开始前,被积函数JVX、JVY中存放圆弧起始点坐标YS、XS,当Y轴产生溢出脉冲(YΔ- )时,JVX作“-1”修正,当X轴产生溢出脉冲(XΔ+ )时,则JVY作“+1”修正,修正的正负方向由圆弧所在的象限及顺逆方向决定。
2)DDA圆弧插补特点:
(1)余数寄存器中初始值为0,JVX、JVY中初始值分别为YS、XS,在插补过程中,JVX、JVY中存放的是动点坐标Yi、Xi,当有脉冲溢出时,动点坐标也应作“±1”的修正。
(2)DDA圆弧插补器中需要两个终点寄存器J∑X积分运算时,余数寄存器每溢出一次,对应的终点寄存器自动减1,直到减为0,则停止积分。
(3)JVX、JVY中数字的大小会影响插补速度。
1.3 插补仿真
采用VB软件对文中的例题进行插补仿真,从而在软件中显示出实际插补轨迹和计算过程,在所有的仿真图中,红色线段表示理论轨迹,绿色线段表示实际插补轨迹。
1)DDA直线插补仿真 以第一象限直线OE插补为例,O为原点(0,0),终点E(4,6),被积函数寄存器(JVX、JVY)与余数寄存器(JRX、JRY)位数均为4,具体的插补过程和仿真轨迹如图3所示。

图3 DDA直线插补仿真
2)DDA圆弧插补仿真 第一象限的顺时针圆弧SE,起点(0,4),终点(4,0),寄存器位数均为3,具体的插补过程和仿真轨迹如图4所示。
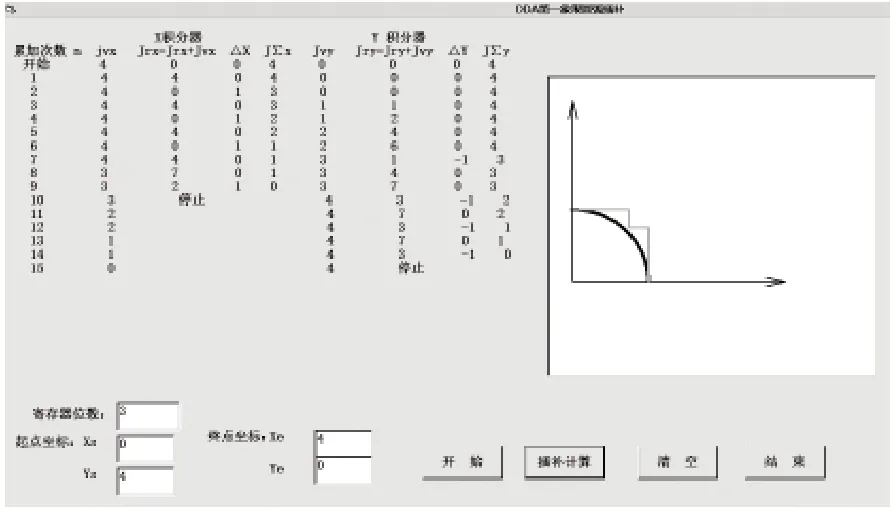
图4 DDA圆弧插补仿真
2 提高DDA插补质量的措施
数字积分法插补中,轮廓的长短不一,使得溢出脉冲不均匀,影响进给速度的稳定性,从而影响插补精度;另一方面,通过仿真软件发现,有的插补轨迹与轮廓之间误差大于一个脉冲当量,因此,为了减小误差,提高插补质量,采用左移规格化法和半加载法。
2.1 左移规格化
所谓的“左移规格化”,将被积函数中的坐标值的前i位零溢出寄存器,使数值成为最高位或次高位为“1”的规格化数,并对其进行累加,从而达到稳定进给速度的目的。
DDA直线插补中,进行左移规格化时,使JVX、JVY中数值同时左移,直到任意一个寄存器中的数值最高位为1,并记下左移次数i,左移规格化后,JVX、JVY中值被扩大2i倍,累加次数相应地减少一倍(n = 2N-i)。
DDA圆弧插补的规格化中,将被积函数JVX、JVY中数值同时左移,直到任意一个数的次高位为1,则为规格化数。如果规格化处理时,左移i位后,当JRX或JRY产生溢出时,JVY或JVX中动点坐标应作“±2i”的修正,为了避免动点坐标修正时溢出,在选择被积函数寄存器容量时,要求必须大于2R(R为圆弧半径),通过左移规格化处理,可使溢出变得均匀,改善DDA插补加工的工艺特性。
2.2 半加载法
DDA圆弧插补过程中,由图4看出径向误差有时可能大于或等于1个脉冲当量,为减小误差,显然可通过增加寄存器的位数N,提高插补精度,但是N的增大,会导致n的增大,累加次数的增加,会降低实际的进给速度,且N也不能无限增大,因此采用半加载法。半加载法即是将余数寄存器JRX、JRY中的初始值设为2N-1,当JRX、JRY与大于或等于2N-1的数进行累加,就可产生1个溢出脉冲,通过半加载后,可以提前溢出脉冲,从而改变溢出在时间上的分布,提高插补精度。
2.3 举例仿真
在1.3节中的直线插补和圆弧插补举例的基础上,采用左移规格化和半加载进行插补计算。
改进后的DDA直线插补仿真中,寄存器位数为5,具体的仿真轨迹和计算过程如图5所示。改进后的DDA圆弧插补仿真中,寄存器位数为5,具体的仿真轨迹和计算过程如图6所示。

图5 左移和半加载后的DDA直线仿真
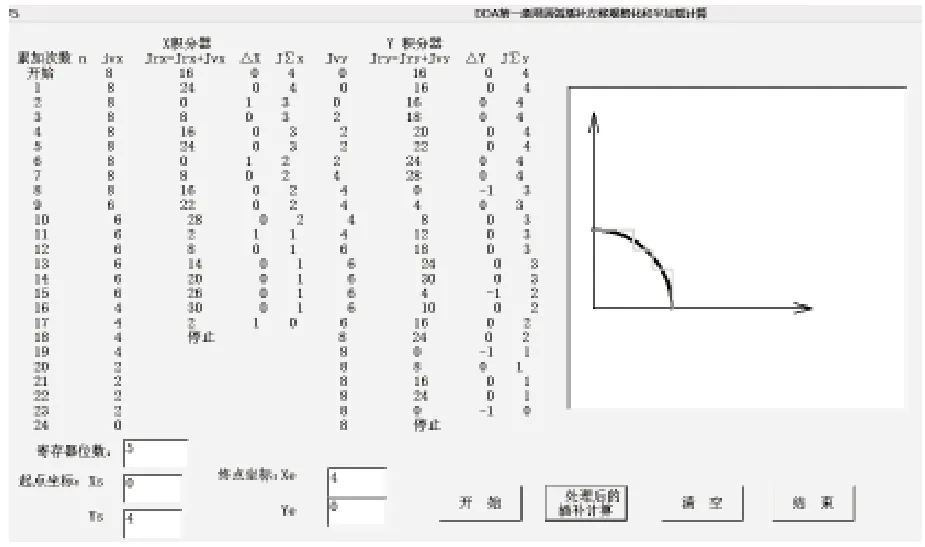
图6 左移和半加载后的DDA圆弧仿真
3 结束语
本文主要讨论了数控系统中的数字积分法的直线和圆弧插补运算,以第一象限直线、圆弧为例,并在此基础上采用半加载和左移规格化进行处理。前后计算过程采用VB软件进行仿真。经过计算过程和轨迹图的比较,发现直线插补处理前要在第三次计算Y轴才有溢出,经过处理后在第二次计算时两个坐标轴就会有溢出;圆弧插补在在半加载和左移规格化后溢出明显提前,且轨迹更接近于理论轮廓,速度和精度都明显提高,该过程的研究对掌握数控机床的运动控制具有重要的理论指导意义,仿真软件对于数控系统插补质量的进一步提高具有极其重要的应用价值。
[1] 汪木兰.数控原理与系统[M].北京:机械工业出版社,2004.
[2] 李恩林.数控系统插补原理通论[M].北京:国防工业出版社, 2008.
[3] 唐友亮,佘勃,袁梦,方军.实现两轴联动的逐点比较法的改进算法[J].煤矿机械,2009,30(12):12-13.
[4] 金中波,张百臣,韩霞,等.逐点比较法直线插补原理及改进算法分析[J].机械工程师,2009(3):126-128.
