引领学生感悟数形结合的思想

陈宁海　李培芳

“数与形”是人教版小学数学六年级上册新增的教学内容，本课意在让学生通过自主探究图形中隐藏着的数的规律，尝试应用所发现的规律解决问题，感悟数与形的广泛联系，同时在利用数形结合解决问题的过程中感悟数形结合的数学思想。显然，数学思想的感悟离不开具体的学习活动，然而，教师该设计什么样的活动？让学生经历怎样的学习过程？让学生在过程中有什么样的体验？凡此种种都值得深入地探索与思考。

一、在深入的数学思考中感悟数形结合的思想

数学思想离不开具体的数学思考，空谈数学思想是没有意义的，只有对数学内容进行深入的思考，才能逐步体会数学内容背后所蕴含的数学思想。在本课的教学中，李老师组织学生在数与形的关联处进行深入思考，并巧妙地引导学生进行深入的比较，让学生在不断的数学思考中自觉去体会、自发去感悟。

【教学片段1】

（一）依数解数：思考25的特征

师：同学们仔细观察25这个数，看看它有什么特点？

生：25是5的倍数。

生：25是5的平方。

生：25是25个1相加。

生：25里面包含5个5。

生：2和5两个数字都有点像鸭子。（同学们笑了）

（二）化数为形：尝试将25转化为形

师：在2000多年前，古希腊的数学家们认为每一个数都是神奇的，都有与众不同的特点。他们就像咱们刚才那样，努力去找25这个数的特点，不过也像咱们这样，找不出25的神奇之处来。不过，通过不断的思考，他们做了一件了不起的事情，他们从地上捡起了25块小石头，然后用这25块小石头摆成了一个图形。猜猜会是什么图形呢？

生：正方形。（让学生用磁扣摆出“形”来）

（三）以形助数：借助形寻找 25的特征

师：将数转化成形后，数学家们找到了25很多神奇的特点。来！咱们也来当一回数学家。老师给大家准备了这样的正方形。

学生借助教师提供的正方形点阵（如下图）寻找25的特征（略）。

生：1+2+3+4+5+4+3+2+1。

生：25=（1+2+3+4）×2+5。

生：25=1+3+5+7+9。

师：这些算式太优美了！

（四）在比较中体会数形结合的思想

师：咱们一起来回顾一下是怎么发现25这个数这些神奇的特点的。起先，咱们就盯着25这个“数”（板书）看，几乎没有什么发现。后来，咱们把25转化成一个“形”（板书），就有了这些神奇的发现。

师：回顾刚才的学习，同学们有什么想说的吗？

生：形的作用太大了。

生：形让我们看到很多数字的特点。

生：因为有形，我们才能发现这么神奇的算式。

生：有了形的帮助，就可以看到光看着数没办法看出来的特点。

生：……

【赏析】

这四个小环节是执教本课的主体部分，是本课的核心环节。教学时，李老师没有使用教材提供的正方形图（如右图），而是选用点阵这一学习素材。这样的选择有其独到之处：一方面点阵更容易通过不同的分法发现其特点，而正方形图就不容易“斜着分”等；另一方面，这样的学习有了古希腊毕达哥拉斯学派的真实的研究为依据，其实是还原数学知识的发生、发现的过程，因而学生的学习过程变得流畅自然。

这四个小环节通过层层递进讲述了一个事实，就是看“数”本身不易发现的特征通过看“形”变得一目了然，这样的学习设计对于学生体会数形结合的意义与作用是很有冲击力的。难怪学生在最后的数形比较中发出了“对‘形’佩服得五体投地”的感慨来。当然，值得注意的是，数形结合的意义不只是在于形可以助数，这只是一个侧面，数形结合还有一方面的意义在于“以数解形”，在这方面最典型的是解析几何，两条直线是否平行，只要写成方程，看它们的斜率就可以判定了，圆也可以写成方程，还有函数图像，等等。这可能是对于六年级的学生是尚无法提及的，然而，教师在这一点上要有清醒的认识，不可偏颇！这样才能给学生一个较为准确的数学知识。

纵观这一学习过程，可以看到学生始终处在有质量、有挑战且持续不断的数学思考之中，学习中此起彼伏的数学问题像磁铁一样牢牢地吸引住他们。在不断地思考中，学生的体验更为深刻。可以看到，在“以数解数”中，学生的思维是受阻的，是困顿的，在“以形助数”中学生的思维瞬间明朗，这种柳暗花明、豁然开朗的思维体验让学生真切地感受到数形结合的神奇与美妙。这种深入的思考与深刻的体验牵引着他们慢慢体会与领悟数形结合的思想。

二、引领学生在数学发现中感悟数形结合的价值

“在人的心灵深处，都有一种根深蒂固的需要，这就是希望自己是一个发现者、研究者、探索者。”（苏霍姆林斯基语）学生的心理特点决定了他们对于成为一个发现者有着强烈的需要，如果数形结合能引发学生的数学发现，那么他们将更能产生对数形结合的价值认同。

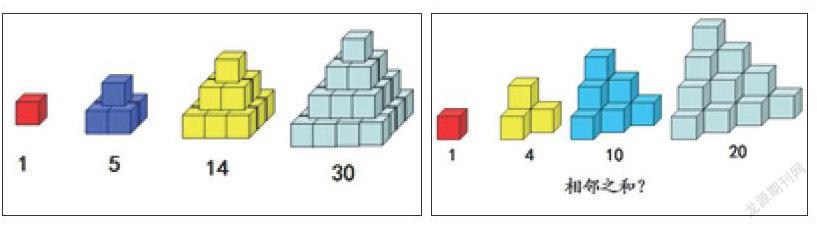
【教学片段2】介绍“神奇的图形数”（三角形数、四面体数、金字塔数等）

课件出示：1，4，9，16

师：同学们，看着这些数，现在我们穿越，回到2000多年前的古希腊，从地上找出石头来，用石头把这些数摆出来，会是什么形状？

生：正方形。

师：给这些数取个名字吧。

生：正方形数。（课件出示下图）

课件出示：1，3，6，10，15

师：接着看，来，穿越，捡起石头来，开始摆。

生：三角形。

师：取个名字。

生：三角形数。（课件出示：三角形数）

师：接着看！（课件出示：相邻数之和）有发现的举手。

生：相邻数之和是正方形数。

生：1+3=4，3+6=9，6+10=16，10+15=25。和都是正方形数。

师：哇！太神奇了！两个相邻的三角形数的和刚好等于一个正方形数！怎么会这样啊？

生（激动）：你看，两个三角形数，如果拼在一起就是正方形数了。（如右图所示）

接着进行金字塔数与四面体数的教学。（如下图，过程同上略）

三、引领学生在反复运用中感悟数形结合的思想

一个知识抑或一个思想其终极的意义可能要使之在实用时得以体现，数形结合的思想也不例外。

【教学片段3】数形结合解决问题

师：由25=1+3+5+7+9想开去，你还能联想出像下面这样优美的算式吗？

生：36=1+2+3+4+5+6+5+4+3+2+1。

生：49=1+2+3+4+5+6+7+6+5+4+3+2+1。

生：64=1+2+3+4+5+6+7+8+7+6+5+4+3+2+1。

生：16=1+2+3+4+3+2+1。

师：真好，这就叫作举一反三。你能找出其中的规律来解决下面的问题吗？

课件出示：1+3+5+7+……（100个连续的奇数）=？

生：100乘100等于10000。

生：16是4个奇数相加，刚好是4的平方。25是5个奇数相加，又刚好是5的平方，所以100个连续的奇数的和就是100乘100，等于10000。（全班鼓掌）

师：看来“形”的作用真是大啊。本来，数和形是分开的。但是今天咱们把它们联系在一起，就有了这么多奇妙的发现。

四、引领学生在大胆想象中感悟数形结合的思想

学数学离不开大胆的想象，甚至是疯狂的想象，想象可以促进发现。在理解了数形结合是什么之后，让学生沿着学习的方向，利用数形结合的思想想开去！让学生看到一片更广阔的数学天地，欣赏不一般的数学美景，这对于他们深入地“悟”数学思想有积极的意义。

（一）在想象中唤醒“数形结合”的已有经验

师：其实，对于数和形的联系，咱们在以前的学习中，也有见过的。想象一下，下面的“形”让你想起什么知识？（出示下图）

生：（7+3）×5。

生：（7+3）×5=7×5+3×5。

生：有点像乘法分配律。

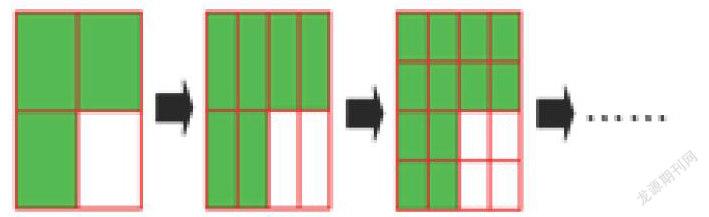
师：接着看，这个呢？（课件出示下图）

生：分数的基本性质。

师：真好！你看，数和形的联系多紧密啊！

（二）在想象中激发“数形结合”探索兴趣

课件出示：展开想象的翅膀

师：请看屏幕！出示数对（3，4），你能猜出这表示什么吗？

生：这可以表示一个点。

师：真好！这个数对可以表示平面上的一个点。这是数学家笛卡尔的伟大创造。自从有了这个天才的创造之后，数与形就更加巧妙地联系在了一起。大家看！（课件出示y=3x+5）

师：大胆想象一下，这可能是什么？（生猜略）

师：你肯定想不到，这是一条直线。

师：再猜，这个呢？（出示y=3x）

生猜略。

师：没错，这也是一条直线。而且这条直线刚好和y=3x+5这一条直线互相平行。

师：还猜吗？最后猜一个！（课件出示：x2+y2=25）

生猜略。

师：你能想象吗？这竟然是一个圆！

【赏析】

“数学思想蕴含在数学知识的形成、发展和应用的过程中，是数学知识和方法在更高层次上的抽象与概括。”学生对于一种数学思想的感悟势必要经历一个从模糊到清晰，从理解到应用的长期的过程，李老师“数与形”的教学，全课以“数形结合”思想为核心，精心选择学习内容，巧妙设计学习活动，让学生经历思考、想象、发现、应用等数学活动，在活动中让学生不断提炼、总结，反复理解、应用。显然，学生只有经历这样的过程，才能逐步悟出数学内容中蕴含的数学思想。

（福建省厦门市华昌小学 361006）