从“长方体体积”看“变教为学”中的学习活动

于桓　郜舒竹

在“变教为学”的备课中，教师应抓准一节课的学习目标，并围绕“学什么”“怎么学”两个问题展开备课。在备课中寻找知识的源头、分析知识的属性，并设计出一系列与之对应的学习活动。

一、对长方体体积的分析

以人民教育出版社出版的《义务教育课程标准实验教科书·数学（五年级下册）》（以下简称“教科书”）为例，长方体体积学习是学生第一次接触立体几何图形和体积概念，这是学生立体几何学习的起始。（见表1）人们常说：“好的开始是成功的一半。”因此，长方体体积的学习对学生今后的发展具有重要的教育教学意义。起始时，学生学习立体图形的好坏程度，决定其今后对立体图形学习的兴趣与动机。小学长方体体积认知程度也将影响着学生初中乃至高中空间几何体的学习。所以，长方体体积学习要求教师在备课中从历史视角、文化视角深入挖掘，发现知识的“本质性”“关联性”“文化性”，让学生知其然并知其所以然。

从历史的视角看，长方体体积公式早在我国著名的《九章算术》第五章“商功章”中有所记载：“方自乘之，以高乘之，即积尺。”[2]意思是用边长和边长相乘再乘以高，就是体积的大小了。由此可见，体积公式很早就被古人发现并使用它计算了。除此之外，《九章算术》中还给出了其他几何体体积的计算公式。比如：球体积。另外，数学课程不仅仅是程序化、模式化反复练习直至熟练的计算和严谨的逻辑推理，数学课程还有它的文化性，这里的文化性是与工具性相对的。强调数学概念背后的故事，概念背后是否与人类思维方式、人的情感有联系。比如：体积是什么意思？体积中的“积”是否和乘积中的“积”一样？“体积”在古代怎么说？《九章算术》第五章讲述几何体的体积，为什么叫商功二字？体积的下位概念，长、宽、高是什么意思？为什么叫长、宽，而不是长、短？这些小问题，都值得教师在备课中思考。

从文化的视角看，乘积中“积”本意是“垛”，[3]而“垛”在《现代汉语词典》中解释为整齐地堆，我们常说的垛子的意思就是整齐地堆成堆。《说文解字》中对“积”的解释为：“积，聚也。”那么，积有整齐地由少到多变化的意思。因此长方体体积可以被看作是由一个个长方形从下至上整齐地堆积而成的，所以命名为体积。“体积”一词在商功章羡除术刘徽注：“虽背正异形，与常所谓鳖臑参不相似，实则同也。”“故方锥与阳马同实。” [4]由此可以看出，体积在古代的叫法是“实”。“实”作为古算用语有多义。实，与“虚”相对之义，它表示内部完全填满而没有空隙的实体。由此，我们可以推断出“实”表示的是空间区域，仅用于三维空间。如果教师在让学生理解概念时，理解它背后的文化，相信对学生的学习会有很大益处。

听课观察中发现，教师问：“同学们，长方形较长的一边叫作长，较短的一边叫什么呢？”学生齐声回答：“短。”长方形中，长、宽这两个概念，表面上看没有什么联系，实质上蕴含着数学文化。“长”在《九章算术》中被解释为“广”，也就是人们视野范围的广度，就是长。而现在所说的“宽”在《九章算术》中被解释为“从”，“从”字在古代又同横纵的“纵”，纵的意思指的是竖、直，南北的方向，与“横”相反。由此可见“宽”字的来龙去脉了。如果教师能让学生知道“宽”字背后的文化，相信学生就不会认为长方形较短的一边叫作“短”了，否则的话，很难说服学生。比如：《九章算术》中第五章讲述几何体的体积，书中以“商功”命名此章。如果光看字面意思，很难理解与体积有什么联系。李籍在《九章算术音义》中写道：“商，度也。以度其功庸，故曰商功。”功，通“工”，指工程量或人工数。大致意思是说，商是度量的意思，度量工程量的多少即关于各种工程中的体积计算。这样就沟通解释了“商功”与“体积”之间的联系。应该相信，虽然概念的命名是人规定的，但是它不是盲目的，一定是和当时人的思维方式、人的情感、社会生活、大自然有所联系而命名的。作为教师，我们应当找到这样的联系并能够解释，沟通字面解释与背后文化的联系。

二、对其他教材的分析

除了从历史、文化的视角分析长方体体积，教师还要关注教科书和课程标准。在我国的教科书中对体积的定义为物体所占空间的大小。美国加州的教材中对于长方体体积的学习，先有对长方体的认识，然后指出长方体的上部、前部、侧面。再利用三视图，从不同角度看长方体，然后给出定义。美国加州五年级教科书中定义为体积是三维空间中所占空间的量，长方体体积被正方体单位（cubic units）测量，长方体体积的学习与维数建立联系。[5]我国现行的《义务教育数学课程标准（2011年版）》（以下简称“课标（2011年版）”）中提出，通过观察、操作，认识长方体、正方体、圆柱、圆锥。结合具体情境，探索并掌握长方体、正方体、圆柱、圆锥的体积和表面积的计算方法。[6]美国加州共同核心标准中指出，学生理解体积要放在三维空间中，理解体积被一个接一个的相同大小正方体的单位（standard units）填满，既没有空隙也没有重叠，在这样的情况下，小正方体单位的数量就是体积的大小。学生要理解长方体的体积被一个个小正方体测量，这也就是当长方体被填满后的小正方体的个数就是长方体的体积。在探索的过程中，分解三维图形，把长方体看成由一层一层的小正方体组成的图形。[7]

《美国学校数学教育的原则和标准》（NCTM）（以下简称“标准”）中指出：“帮助并加强学生在测量二维和三维图形时发展几何直观。”[8]由此可见，在实际教学中教师应在观察、操作的基础上以实验几何为主线探索长方体体积公式，建立学生的三维空间观念，发展学生的几何直观。

长方体体积的学习实际上是建立学生三维空间观念和发展几何直观的起始，在今后初中学段，学生还会接触到更多的几何体，比如：球、六棱柱、四棱锥等。还会从不同角度观察其他不规则几何体，绘制三视图。初中主要是对柱、锥、球进行初步认识。高中学段，要对柱、锥、台、球、简单几何体的结构特征有所把握，学习中心投影和平行投影，并在平行投影下从不同角度观察空间几何体，利用斜二测法绘制空间几何体的直观图，计算空间几何体的表面积和体积及简单几何体的体积。由此看出，体积的学习是层层递进、一脉相承的，从简单的长方体体积的计算，再到柱体、锥体、台体、球体及组合体的计算，学生的空间几何观念，也随着年龄的增加不断增强。

三、教学中的活动设计

根据瑞士心理学家让·皮亚杰提出的“学生有逻辑的理解概念要在学会数学计算之前”[9]的观点，也就是说学生概念理解比计算重要得多，所以本节课的总目标制定为明晰体积概念，探索体积公式。体积属于规律性知识，也就是不以人的意志为转移的客观存在，对学习者来说是确定的，这部分知识具有“不可变”的特点。所以认识这部分知识的基本方法是发现（discover），而发现知识的重点要放在“观察”上。学生的思维方式应该是观察对象形成动机、产生想法、交流、假设、实验与解释、判断、关联与应用的过程。根据这样的基本原则，那么学生就要经历以下学习活动。

第一是建立观察对象、激发学生的动机。动机与兴趣是学生学习的动力，激发学习动机是非常关键的一步。因此，在教学一开始，教师可以给学生讲一个故事。

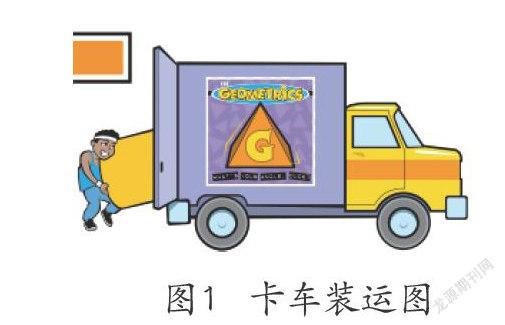
一个非常有名的乐队叫作几何家族，他们计划在学校开一场音乐会，现在需要用卡车运送搭建音乐会舞台的器材，需要将一个个正方体的箱子装进长方体的卡车中。（如图1）

这个过程处于课程刚刚开始阶段，学生要做的是观察，观察教师演示的过程。教师可以用一个大长方体鱼缸模拟卡车，然后依次放入一个个小正方体，让大长方体被一个个小正方体填满，复现故事场景。这个过程从知识习得的角度和历史的角度来说，是为了让学生体会到体积在古代被称为“实”，表示内部完全填满而没有空隙的实体。让学生利用小正方体模具是根据著名瑞士心理学家让·皮亚杰提出的认知发展理论（Theory of Cognitive Development）。他将儿童的认知发展过程分为了四个阶段，分别是感知运算阶段、前运算阶段、具体运算阶段、形式运算阶段。[10]五年级的学生认识体积概念处在具体运算阶段（Concrete Operational Stage），学生的思维阶段是从具体的、形象的表象思维逐渐过渡到抽象思维。这一时期的顺利过渡，会对儿童学习“体积”、对抽象概念的理解起到重要作用。在这一时期，儿童在心理发展和思维特征上具有逻辑性，但是在具体活动中仍然离不开具体事物的支持。这一原则将成为儿童思维水平的判断依据，也是教师教学设计的重要理论依据，在具体的教学实践中，教师要以具体事物作为儿童理解体积并推导体积公式的依托。

第二是产生想法。任务一是通过刚才教师的演示，你观察到了什么？你是如何看待长方体的形成的？长方体体积如何计算？四个人一小组，可采取画图、用文字写下来等多种形式和同伴相互讨论。经思维碰撞后对于体积公式的答案是唯一的，但是表达形式可能是多元的，所以，教师应允许多元的表达，多样的形式。在用不同的活动形式进行充分讨论之后，学生要以小组为单位给全班汇报展示，并说说本组每一位同学的想法。这种活动形式具有较强的灵活性。

第三是实验解释。任务二是利用小正方体模具解释如何理解长方体体积的形成，利用小正方体模具解释体积公式是如何得到的。学生可能会演示并解释小正方体填满长方体的过程。（如图2）先从一个小正方体拼成一行，从一行再到一个面。三个同样的平面叠加，填满整个长方体，最终得到一个完整的长方体，小正方体的个数也就是长方体体积。

之所以让学生解释长方体体积的形成过程，是根据荷兰数学教师范希尔夫妇提出的几何思维水平理论。其中包括学生几何思维发展的五个水平和与之对应的学生几何学习的五个阶段。[11]学生几何思维发展的五个水平分别是视觉化（visualization）、分析（analysis）、非形式化演绎（inference）、形式化演绎（deduction）、严密性（rigor）；与之对应的学生几何学习的五个阶段分别是熟悉（familiarization）、指导定向（guided orientation）、语言表达（verbalization）、自由定向（free orientation）、整合（integration）。五年级学生处在几何思维的分析期，并由分析期逐渐转化为非形式化演绎期。所以，在长方体体积的概念学习上，要让学生经历体积概念的分析和理解过程，并对体积形成过程进行简单的非形式化演绎，这是教师教学设计的重要依据。学生对概念的学习不是简单的“听懂、记忆、背诵”过程，深入理解、消化概念，明晰概念背后的本质，对学生今后学习几何知识具有重要意义。在公式的探索方面，让学生经历非形式化演绎的过程，明确长方体体积公式的产生。在这个环节中，活动形式为先小组讨论再全班汇报。在汇报的过程中，教师要给学生立规矩。比如：“汇报的同学要面向大家，说话要保证班里的每一位同学都能听清楚。”“当你想指出别人不足的时候，请先说出他的一个优点。”教师引导学生，先说他人优点再指出他人的不足之处。另外，小组汇报是提高学生当众讲话能力的好机会，这种活动方式有助于培养学生的自信心和演讲能力。

第四是判断假设。根据上一个任务全班同学完成的情况，判断大家说的长方体体积的对错，是否同意汇报同学的观点，是否有其他的异议。

第五是关联应用。结合相应的练习题，学生独立思考并计算长方体体积。

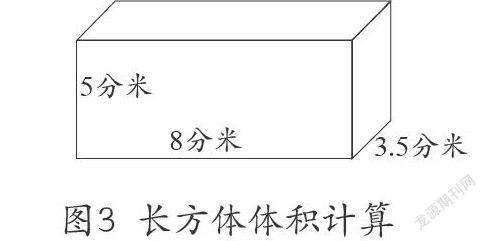
比如：一个汽车上的油箱，长8分米，宽3.5分米，高5分米，这个油箱可以装多少升汽油？（如图3）

第六是拓展。任务三是有人说：“周长与面积之间有某种关系，表面积和体积也有某种联系，你同意吗？”“解释正方体体积的形成过程，写出正方体体积公式。”这个任务布置的目的是让学生试图探索长方体体积和长方形面积之间的关系。从已有周长和面积入手，周长反映物体外部而面积反映物体内部，而表面积和体积恰巧也有“外”与“里”的关系。这样就把周长与面积、表面积与体积联系在一起了，在英文文献中也有记载表明，学生在学习的过程中要理解四个概念之间的联系。[12]

以上教学活动仅供教师参考，教师可根据本班学生情况而定。依据以上分析，本节课关于学习目标、学习任务、学习方式和学习活动的设计可以用表格（表格略）的形式呈现。

总之，要想在变教为学的课堂中“突出本质、渗透文化、实现关联”，就要挖掘知识背后的故事，要想“让每一个学生受到关注，让每一个学生都有机会，让每一个学生都有活动”，就要设计出以“立德树人”为终极目标，并能突出数学本质的有效的活动。

参考文献：

[1] 卢江，杨刚.义务教育课程实验教科书·数学[M].北京：人民教育出版社，2004.

[2] 张苍，等编.九章算术[M].曾海龙，译.江苏：江苏人民出版社，2011.

[3] 郜舒竹.问题解决与教学实践[M].北京：首都师范大学出版社，2012（06）：168.

[4] 李继闵.九章算术导读与译注[M].西安：陕西科学技术出版社，1998.

[5] California Mathematics Grade 5[M].The United States.McGraw-Hill Companies，2009：396.

[6] 中华人民共和国教育部制定.义务教育数学课程标准（2011年版）[S].北京：北京师范大学出版社，2012.

[7] California State Board of Education. California Common Core State Standards Mathematics[M]. California Department of Education，2010.

[8] 全美数学教师理事会著.美国学校数学教育的原则和标准[M].北京：人民教育出版社，2004.

[9] Piaget，J，Inhelder，B.&Szeminska，A.[Translated from the French by E.A.Lunzer]，.The Child’s Conception of Geometry[M].New York： Basic Books，Inc，Publishers.1970.

[10] 莫雷.教育心理学[M].北京：教育科学出版社，2007.

[11] 鲍建生.数学学习的心理基础与过程[M].上海：上海教育出版社，2009.

[12]Joan D.Martin. A Study of Fourth Grade Students’ Understanding of Perimeter， Area， Surface Area， and Volume When Taught Concurrently[J].Mathematics Education Tufts University，2009（05）：3354724.

（首都师范大学初等教育学院 100048）