怎样展开纸盒才使周长最小？

有这样一道题：有一个长方体纸盒，长为5厘米，宽为3厘米，高为2厘米.小明想把长方体纸盒剪开得到其表面展开图，则小明要剪开______条棱，所得到的表面展开图的周长最小是______厘米.

长方体一共有12条棱，6个面，展开图中需要留下5条棱以连接这6个面，因此，无论怎样剪开，都需要剪12-5=7（条）棱.

要想使得展开图的周长最小，尽量应保留较长的棱.如图1所示，我们打开长度为5的棱，保留剩下的3条，保留2条长度为3的棱，剩下的7条棱全部剪开，因此展开图的周长是5×2+3×4+2×8=38（厘米）（如图1）.

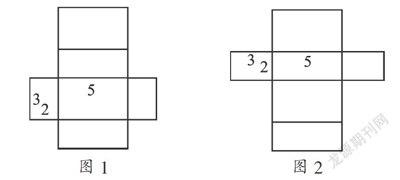
对于其他的展开方式，如图2，展开图的周长是5×2+3×8+2×4=42（厘米）.

如果是图3，则周长是5×4+3×2+2×8=42（厘米）.

如图4，展开图的周长是5×8+3×2+2×4=54（厘米）.

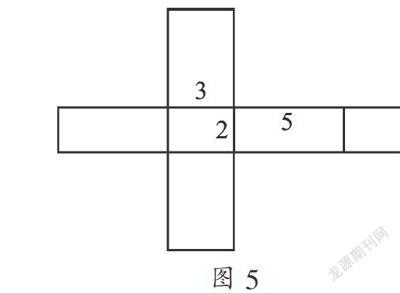
如图5，周长是5×8+3×4+2×2=56（厘米）.还有一些其他的图形，不再一一叙述.

我的解题感悟：我们在学习中，解决完一个问题，最好能想到与此相关的更多的问题.

教师点评：数学学习最可贵的是“举一反三”，思维的开阔性可以在以下方面尝试：问题还有其他情形吗？反过来怎么说？问题的一般情况如何？陶宇阳同学在解决问题的过程中丝丝入扣，步步为营，显示了扎实的数学功底.其实，这个问题还可以继续探究下去：把结果推广到一般情形：若c

长宽高分别是a、b、c（c

（指导老师：吴寿根）