透过现象看到本质

姜荣富

初等几何研究的立体图形包括棱柱、棱锥、棱台、圆柱、圆锥、圆台、球等。其中圆柱、圆锥、圆台都是旋转体。以长方形的一边或直角三角形一直角边所在的直线为旋转轴，其余各边旋转而形成的曲面所围成的几何体，分别叫作圆柱和圆锥。不仅如此，利用平面图形和它的运动，可以方便地定义相关的概念。旋转轴是它们的轴，在轴上的这条边叫作它们的高，垂直于轴的边旋转成的圆面叫作底面，不垂直于轴的边旋转成的曲面叫作侧面，无论旋转到什么位置，这条边都叫作侧面的母线。

古希腊的几何学家对圆、球、柱、锥进行研究，而且还对其他的多种曲线如椭圆、抛物线、双曲线等等的性质进行研究，获得杰出的成果。[1]这三类曲线统称为圆锥曲线，是数学研究的重要对象。小学生认识圆柱与圆锥，学习相关的测量，为进一步研究圆锥曲线的性质打下基础。下面从概念引入、转化方法与学生理解三个方面，讨论教材的设计，比较不同教材的编排方式，分析学生的理解与掌握情况。

一、概念的引入：分类与抽象

不同教材引入圆柱与圆锥的方式大致可以分成两类：一类是从图形的分类中引入，一类是从实物的抽象中引入。

从分类中引入。教材提供众多的直柱体与正锥体，让学生按一定的标准进行分类，在分类的活动中认识圆柱与圆锥区别于其他柱体与锥体的特征。如韩国2006年修订的《数学课程标准》，在小学六年级图形的教学内容中，安排了角柱（棱柱，下同）与角锥（棱锥，下同）的性质、圆柱与圆锥的性质，[2]在认识棱柱与棱锥的基础上学习圆柱与圆锥。台湾版《国民小学数学课本》第十一册（南一书局企业股份有限公司，中华民国九十一年八月版），以“角柱与角锥”为单元标题，先是提供了各种各样的直棱柱与正棱锥，按照是否有尖顶分成柱体和锥体，再根据底面形状把柱体分成圆柱与角柱。如下图：

无论是研究问题还是认识图形，分类都是重要的。通过以上两级分类，学生可以把柱体与锥体、圆柱与棱柱清晰地区分开来。认识图形不仅仅是为了让学生知道哪一种图形叫什么名字，学会区别图形，更重要的是让学生学会对图形分类，认识某种具体图形的教学只是个案，只有让学生理解图形的分类才使教学具有一般性。[3]分类的核心是建立分类的标准，只有那些可以作为分类标准的性质才是图形的重要特征。在分类的过程中，既要关注图形的共性，也要关注图形的差异，而共性和差异都是抽象的结果，是抽象的具体体现。[4]因此，分类不仅是学生认识图形的手段，也是培养学生抽象能力的途径。

从抽象中引入。从实物图形中抽象出几何体，也是认识几何图形的重要方法。这个抽象的过程，舍弃了图形的颜色、材质等物理属性，只保留空间、大小、位置等数学属性。国内的教材大多采用这种方式来引入圆柱与圆锥。如人教版教材（下左图）与北京版教材（下右图）：

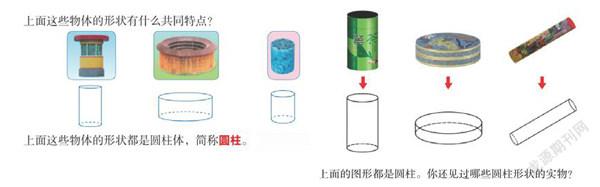
不过，抽象似乎并没有确切的定义，从实物图抽象到几何图，究竟哪些属性应当保持不变，不同教材其处理的方式也有差异。以上两个版本的教材，实物图与几何图形的大小是一致的，或者说抽象前后基本保持1∶1的大小比例关系。以前的教材似乎并不注意这一点。如下图：

笔者的理解是数学中的抽象也是分层次的。如果从不同大小的实物图形中抽象出一个几何图形，属于比较高层次的抽象，这时抽象得到的几何图形具有“类”的特征。换句话说，从大小不同的实物中抽象得到的几何图形，只是数学研究的对象，在现实世界中并不真实存在。

二、转化的方法：立体与平面

认识立体图形的基本思路是转化为平面图形。我国《义务教育数学课程标准（2011年版）》要求：通过观察、操作，认识圆柱与圆锥，认识圆柱的展开图。[5]这些观察、操作的活动主要是图形的观察比较，图形的展开折叠，平面图形的旋转，立体图形的截面，等等。从教材的呈现上看，包括看一看、比一比、转一转、做一做、截一截。

看一看。观察是认识图形最重要也是最基本的方法。如下图人教版教材：

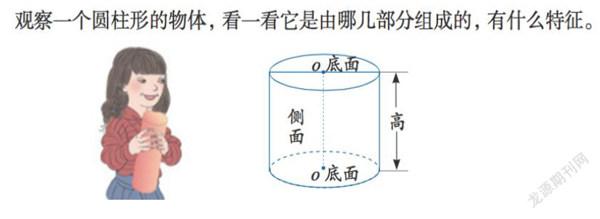
学生在认识图形的过程中，积累了许多观察图形的经验，比如分析平面直线图形可以观察它的边与角，分析长方体可以观察棱和面的大小与位置关系，这些经验不容易直接迁移到认识圆柱的活动中来，教材需要设计更加直观与丰富的活动。

比一比。圆柱与圆锥联系密切，同底等高的圆柱体与圆锥体的体积存在确定的倍数关系。通过对这两类立体图形进行比较，学生容易找到它们的相同点与不同点。北师大版教材把认识圆柱与圆锥安排在同一课时，使比较成为认识图形的现实途径。如下图：

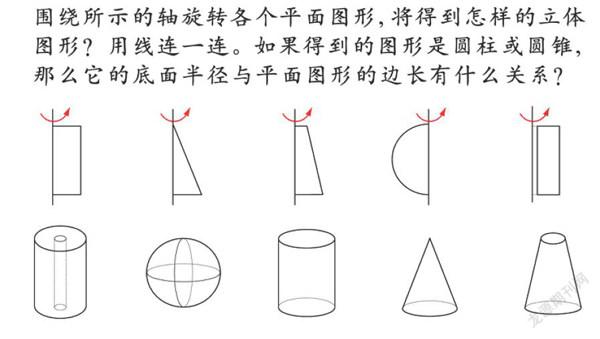
转一转。由平面图形旋转得到立体图形，这是旋转体独有的特征，这种特征体现了平面与立体的奇妙关系，也为学生认识立体图形的特征提供了新的视角。许多教材都安排了将平面图形进行旋转的活动，浙教版教材在要求学生观察想象的同时，还要进一步思考平面图形的边长与立体图形底面半径的关系。如下图：

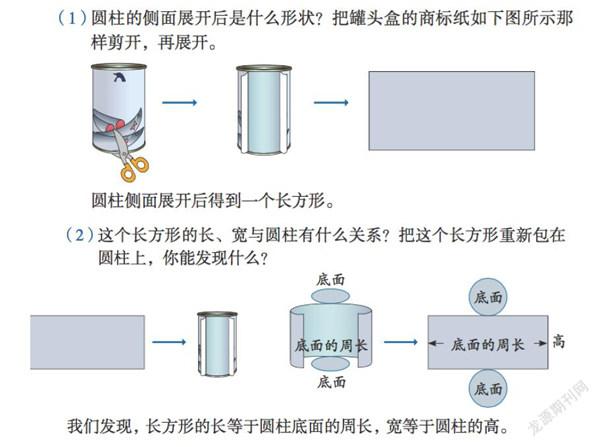
做一做。把立体图形转化为平面图形进行研究，比较直观的方式就是展开与折叠。人教版教材在学生初步认识圆柱的特征之后，通过展开与折叠的活动，发现立体图形的组成元素与平面展开图之间的关系，为学习表面积计算打下基础。如下图：

截一截。用一个平面去截立体图形，也是认识立体图形性质的一种途径。如下图北师大版教材：

朗文出版社出版的《小学数学》，在6A学段呈现了丰富多样的圆柱或圆锥截面。如下图：

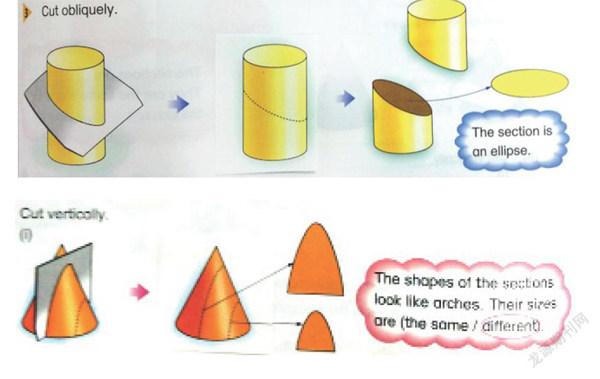
对于圆柱，用一个垂直于旋转轴的平面去切割，所得的截痕是一个圆，如果割面和转轴不垂直，则截痕是一个椭圆。对于圆锥，用一个垂直于旋转轴的平面去切割，所得的截痕也是一个圆，如果割面和转轴不垂直，则截痕是椭圆、抛物线或双曲线。

三、学生的理解：特征与反例

为了解学生对圆柱特征的理解水平，笔者对浙江省某城镇小学六年级两个班的113名学生进行了测查。教学使用北师大版教材，两个班由同一个教师执教。测查安排在上完“面的旋转”这节新课之后进行，时间20分钟。测查题目为北师大版教材第4页的一道练习题，如下图：

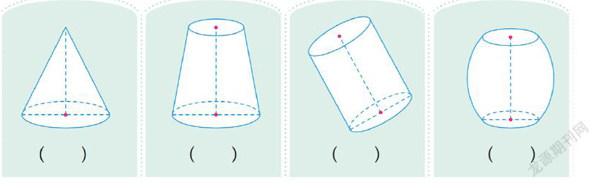
测查的问题是：上面的图形哪些是圆柱体，哪些不是？想一想圆柱有什么特点，用自己的话写下来。

主要从两个方面进行分析：一是学生对图形特征的描述是否完备？二是反例是否支持学生改善特征描述？

圆柱的组成元素包括底面、侧面、高等，这些元素包括形状、大小、空间关系。这项研究主要考查学生从哪些角度描述圆柱特征，研究的方法是对学生描述的特征进行归类分析。主要包括：（1）底面是形状一样、大小相同的圆；（2）侧面是曲面，展开是长方形；（3）有无数条高，这些高都相等；（4）由长方形旋转得到，是圆平移的轨迹。结果如下：

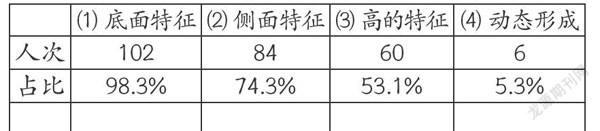
可见，对于底面的特征学生比较容易把握，而对于圆柱的动态形成过程印象并不深刻。其中，特征描述中包含（1）（2）（3）这三项的有34人，占30.1%。可以这样说，这部分学生对于圆柱特征的描述比较完备。或者说，与那些“顾此失彼”（只描述一项或两项）的描述相比，约1/3的学生对圆柱特征的描述比较完备，可以理解为他们对图形特征的掌握比较好。

正例与反例对于概念学习有各自不同的价值，正例用于概括，反例推动反思。调查时先让学生独立写下圆柱的特征，然后提示学生：再想一想，你写的话有没有把上面不是圆柱的例子排除在外，如果没有排除外，应当怎样修改你写的话。对113名学生进行分析，描述中包含了许多错误或不够清晰、严谨的地方，但在教师提示学生对照反例后，对描述作了修改的有23人，占20.4%。这样看来，反例对学生改善图形特征的描述所起的作用比较小，这是在教学时需要引起注意的地方。

“透过现象看本质”是一句至理名言，它对数学概念教学也有启示意义。教材提供的实物或几何图形，各种属性是混杂在一起的，它是“现象”。抽象、分类、转化与概括正例、思考反例，这些活动就像一个个筛子，把本质属性与非本质属性分离开来，帮助学生“看透”概念的本质，形成对图形特征的理解。

（注：本文作者系朱乐平名师工作站一课研究组成员）

参考文献：

[1]项武义著.几何学的源起与演进[M].北京：科学出版社，1983：130～131.

[2]曹一鸣主编.十三国数学课程标准评介[M].北京：北京师范大学出版社，2012：224.

[3][4]史宁中著.小学数学教学中的核心问题——基本概念与运算法则[M].北京：高等教育出版社，2013：57.

[5]中华人民共和国教育部制定.义务教育数学课程标准（2011年版）[Z].北京：北京师范大学出版社，2012：23.

（浙江省新思维教育科学研究院 310003）