由一道考题引发的思考
2015-09-10蓝雪敏
蓝雪敏
一、“好题坏题”引观点之争
数学试卷题,作为考查学生掌握数学知识和思想方法、思维的灵活性的重要手段,对教师的教和学生的学具有重要的示范性和导向性作用。平时,大多数教师都是根据教材内容而制定相应的教学预案,围绕课本习题展开,渗透相关的数学思想方法。然而,一次考试的一道选择题,引起了笔者对教材的重新思考。2014年衢州市六年级下册期末试卷中有一道选择题:见图1,在给定的正方形点子图上,找一点D,使ABCD是一个梯形,D点共有( )种不同的选法。
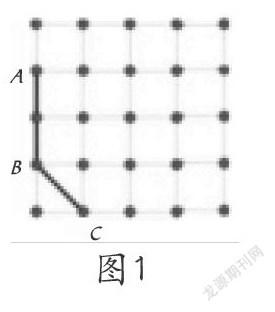
A.2 B.3 C.4 D.5
图2中①至⑤为5种正确答案,⑥是平行四边形。
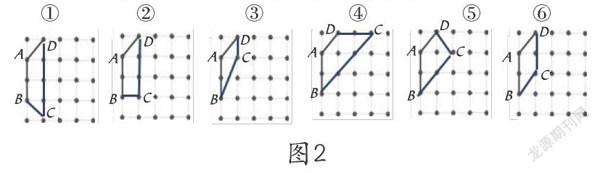
考试后统计正确率只有20%(参加考试360人,错误288人),事后访谈学生解答错误原因:
1.读不懂题意20%,计57人。
2.只考虑到以AB边为上底,没有考虑到BC也可以作为上底70%,计202人。
3.说题出错了,一共有6种,没有考虑到⑥是平行四边形10%,计29人。
事后,教师们提出了自己的看法:
观点一:此题太难,既要考虑已知边AB和BC都可以作为梯形上底,又要排除其中平行四边形这一特例,学生理解困难,要求过高。
观点二:这是一道难得一见的好题,既综合了梯形和平行四边形的特征,又考查了学生的空间观念和灵活解题能力。
二、“透过现象”析背后之因
这道选择题属于“空间与图形”领域的知识,重在考查学生的空间观念。《义务教育数学课程标准(2011年版)》指出:在空间与图形的教学中要“丰富对现实空间及图形的认识,建立初步的空间观念,发展形象思维。”面对20%的得分率,如何在“空间与图形”的教学中“把握知识本质特征,培养空间观念”引起了笔者的深刻反思。
(一)教材层面
北师大版四年级下册教材第29页“四边形分类”这一内容中先让学生“分一分”,直接告诉学生①③和⑥为一类(平行四边形),②④和⑦为一类(梯形),⑤和⑧为一类(一般四边形),接着引导学生想一想“智慧老人为什么这样分”,得出平行四边形和梯形的概念,然后在比较中引出长方形和正方形都是特殊的平行四边形。这样安排的好处是充分考虑到四边形之间的联系,容易在大量的知识冲突中辨清图形之间的联系与区别,但缺点是学生对于平行四边形和梯形的特征都是通过观察获得的,梯形只有一组对边平行的特征的建立比较肤浅,学生建立的表象过于单一。
(二)教师层面
在教学中,部分教师仍然把“掌握梯形的特征”作为教学的主要任务,强调“只有一组对边平行”,却忽视“为什么”,把发展空间观念当成教学的“附属”。很多教师都认为,图3中的③④和⑤位置发生了变化是学生最难理解的,⑥符合梯形的特征,学生不难理解。事实果真如此吗?
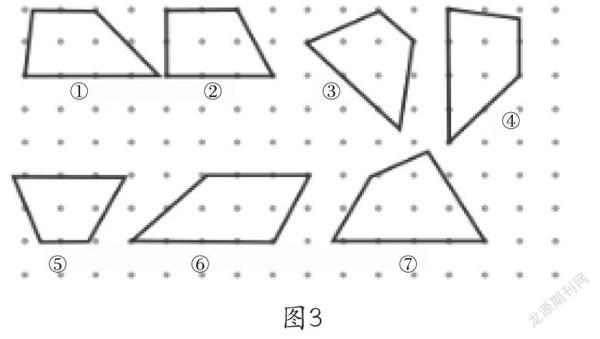
(三)学生层面
在四年级教学梯形前,笔者以上图做了前测,统计结果如下:

通过访谈,学生认为:图6和生活中见过的梯形(堤坝、木梯)的样子不像,图7很像生活中见过的梯形。可见学生对于梯形的认知仍停留在生活经验层面,导致认知的偏差。
以上种种原因,再碰到前文的题型灵活多变,得分率低也就不足为奇了。
三、“正本清源”寻有效之方
基于教材、教师和学生的真实情况,对于“梯形的认识”一课有必要进行整合调整,笔者认为可设计“起→承→引→合”的探究过程,由浅入深,课始重在明晰梯形“只有一组对边平行的四边形”这一本质特征;课中由静到动,多角度各位置认识各类梯形,让静态的知识动起来。这样方能有效培养学生空间观念。
(一)起——巧妙链接,激活经验
“起”则为开端。在这里是指巧妙链接,激活经验,导入新课。
由于学生已经掌握了平行四边形是“两组对边分别平行的四边形”这一本质特征,因此,课始借助回忆平行四边形的特征,用课件出示三角形和平行四边形重叠而成的图形引入新知(图4),激活学生已有的生活经验,有效导入新课,为后续的教学奠定基础。
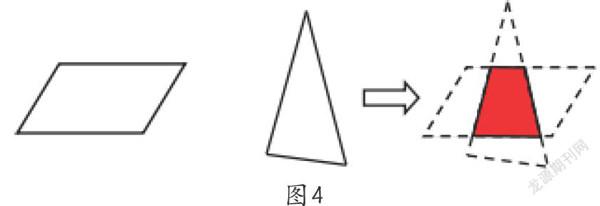
1.找准异同,合理组合
梯形与平行四边形的本质区别在于,前者只有一组对边平行且另外一组对边不平行,后者有两组对边分别平行。在教材的安排中,学生对于梯形的特征都是通过观察获得的,表象建立单一,教师往往只是强调概念中的“只有一组对边平行”,却忽视“为什么”。运用平行四边形和三角形重叠成梯形,梯形的本质特征跃然纸上,为新知的建构搭造了平台。
2.基于教材,匠心独具
在平行四边形和三角形的重叠中引出梯形,学生发现这个四边形的一组对边是原来平行四边形的一组对边,所以它们是互相平行的,而另一组对边是原来三角形的两条边,它们是不平行的。这样的安排匠心独具,创造性使用教材,学生既知其然,又知其所以然,学得轻松自然。
(二)承——妙引体验,逐步感悟
“承”则为承接。在这里旨在承接导入的情境,进行灵活变换,解决相似的问题。在这个过程中,要循序渐进,以免学生的思维出现断层;同时,为后续空间观念的培养作铺垫。
1.简单变化,初步感知
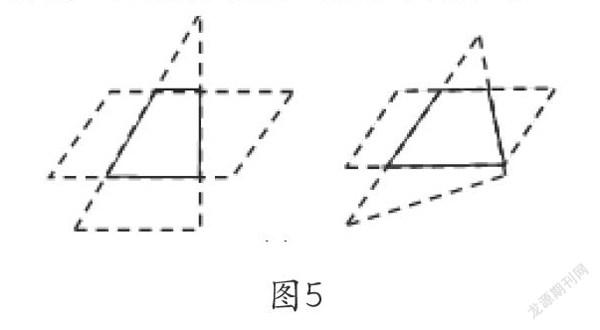
动画演示图5两种组合:重叠部分是梯形吗?与平行四边形有什么不同?明确这两个梯形上下对边平行,左右对边延长线相交,初步认识“只有一组对边平行的四边形是梯形”的本质特征。
2.改变位置,理解本质

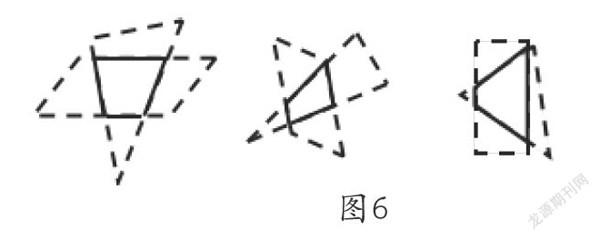
在梯形的判断练习中,认识像“”这类梯形对于学生来说是个难点,因此,在初步感知梯形特征后,改变摆放位置,出示图6:重叠部分是梯形吗?为什么?在三角形与平行四边形的重叠图中认识梯形,形象地揭示了梯形“一组对边平行,另一组对边不平行”的本质特征,点出了梯形与平行四边形的联系与区别。科学地诠释了梯形的意义,学生一目了然,印象深刻,梯形的特征自然深深地印在脑海中。为了防止思维定势,既有常规图,又有变化图,普通梯形、直角梯形和等腰梯形一一呈现,为下面的学习埋下伏笔。
3.联系生活,加深印象
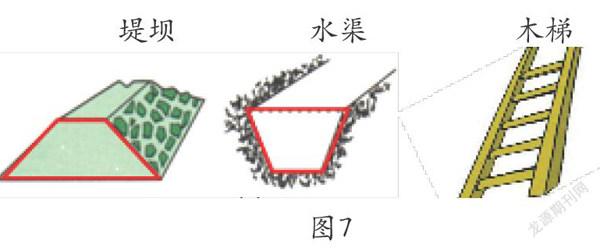
在理解梯形本质特征后,与生活实际相联系,引导学生从“形”的角度观察周围的事物,发现梯形就在我们生活中,加深对梯形特征的认识,体会到数学与生活的密切联系:生活中你见到过哪些梯形?你能找出图7中的梯形吗?引导学生数一数木梯中梯形的个数,不着痕迹地渗透有序思考、合理迁移的数学方法。
(三)引——引学结合,深化新知
“引”则为引导。在“起”“承”的基础上,进行有效的“引”,让学生主动参与是关键,运用梯形本质特征学习新知,进一步培养学生的空间观念。
1.火眼金睛,辨析明理
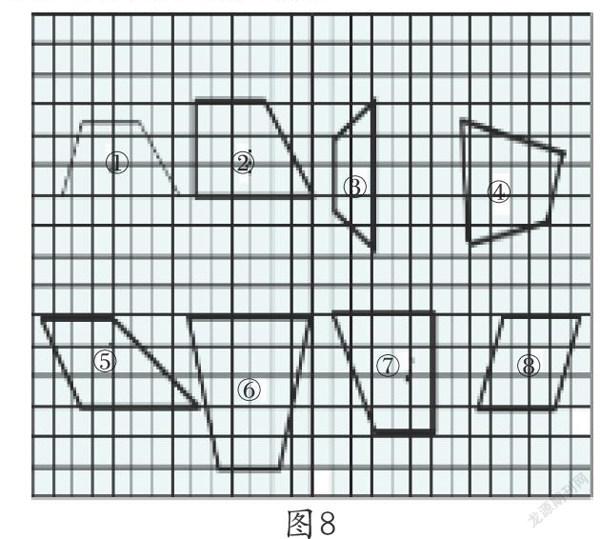
学生利用刚刚获取的知识,在四边形中寻找梯形:图8中的图形哪些是梯形?哪些不是?为什么?在观察、思考、质疑中巩固对梯形的认识,培养分析能力和综合能力,在辩论中结合正反两方面的例子加以说明,不断完善对梯形的认识,在比较中加深对梯形本质特征的印象。
2.动手操作,突破难点
课件隐去上图中图④和图⑧:梯形有什么相同点呢?(梯形都有一组对边平行,另一组对边不平行),在交流、讨论中认识底和腰;引导学生认识梯形的高,找一找梯形的高后独立画高,在比较中明晰高的正确画法;课件呈现三角尺在上下底之间来回移动:梯形的高有几条?为什么?通过动手操作和比较,突破认识高和画高难点,使抽象的知识形象化。
3.挑战自我,一刀成形
根据梯形的特征,利用一张长方形纸,一刀剪出一个梯形:这个梯形有什么特征?这是一道开放题:这一刀不是任意的一刀,必须破坏一组对边平行,第一种剪出直角梯形,特别是第二种剪法需要将长方形对折一次才能剪出一个等腰梯形。这一操作活动,增加了挑战性!学生根据“梯形只有一组对边平行”进行推理,在操作、想象、推理中,学生在长方形和梯形间来回“穿梭”,既巩固了梯形的概念,又巧妙地引出了直角梯形、等腰梯形,在活动中自然发现了两种梯形的特征(直角梯形有两个角是直角;等腰梯形两腰相等,底角相等,是轴对称图形),认知体系逐步建构和完善,空间观念得以培养。

(四)合——活用练习,内化思想
“合”则为结合。在这里是指结合前后知识,内化本质特征,进一步培养空间观念。空间观念的培养需要一个循序渐进、由浅入深的过程。在这一过程中,能结合课堂内外,结合前后知识,不断“拨动”学生的思维,就可让学生的学习得以不断地积累、感悟、明朗,直到主动应用。
1.分类建构,形成体系
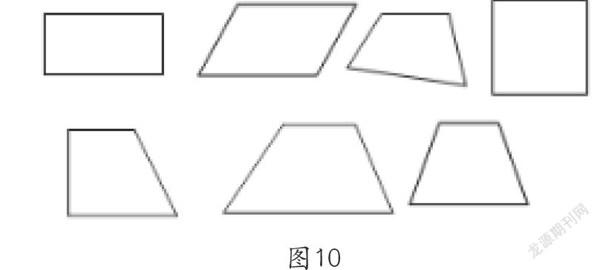
学生形成的空间观念应该是“整体的、深刻的、概括的”,即一旦需要提取这一观念就应该是鲜明的形象,而且是总体、简约地出现。学生回忆所学四边形后,试着把图10中的四边形分分类,学生把所学过的平面图形利用不同的标准分类,既利用了梯形与其他四边形的区别进一步巩固了梯形的特征,又将所学过的平面图形的知识进行了整理,建构了平面图形的知识体系。这一过程进一步促进了整体的、深刻的、概括的空间观念的形成。
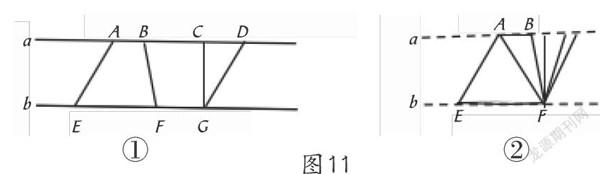
2.推陈出新,前后纵连
新授课的练习既要紧扣本课重点,又要推陈出新,带有一定的挑战性,同时兼顾生动有趣,易于理解。先后呈现:直线a与直线b互相平行,下图中有几个梯形?把它们指出来(图11①)(图11①中共有梯形ABFE、梯形BCGF、梯形ACGE、梯形BDGF四个和一个平行四边形ADGE);几何画板演示:BF不停地移动,可以看到哪些图形?(图11②)(设计图11②的目的在于复习已学多边形,图形虽然不同,但每个图形的高都是一样的)两题呈现了已学多边形,需要学生擦亮双眼、汇报分享、集体共议,使学生深刻认识所学多边形的本质特征,沟通几种多边形之间的内在联系,从而建立科学的认知结构,使得空间观念的建立由静态走向动态。
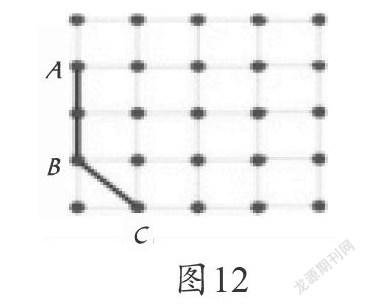
3.意犹未尽,延伸课外
数学学习首先要理解,然后在理解的基础上运用所学知识解决问题。课末,同桌合作,在钉子板上围一围(如图12):找一点D,使ABCD是一个梯形,点D共有多少种不同的围法?激发学生思考,并延伸到课外,掀起新一轮的探究,在反复实践应用中,空间观念得到培养。
总之,学生空间观念的培养不是一蹴而就的,需要教师以生为本,准确定位。教学中从图形的本质特征出发,采取多种教学措施,引导学生在活动中积累空间与图形的学习经验,引导有序思考,必能促进其空间观念的增强。
(浙江省龙游县教育局教研室 324400)
