在错误中学到更多
2015-09-10彭利民
彭利民
统计与概率是中考必考的知识,它主要是以实际应用问题为载体展现. 同学们常会感到初学并不困难,可一旦遇到具体问题,却时常出错. 本文就以统计与概率解题中几个易混淆的问题为例予以剖析,以期对同学们的学习有所帮助.
一、 对频率、概率的理解有误
例1 如果事件A发生的概率是,那么在相同条件下重复试验,下列叙述中,正确的是( ).
A. 说明做100次这种试验,事件A必发生1次
B. 说明事件A发生的频率是
C. 说明做100次这种试验中,前99次事件A没发生,后1次事件A才发生
D. 说明做100次这种试验,事件A可能发生1次
【错误解答】B.
【错解成因】在相同的条件下,进行了n次试验,在这n次试验中,事件A发生的次数m称为事件A发生的频数,比值称为事件A发生的频率. 由此可见,频率跟试验的次数有着直接的关系,试验的次数不同,得到的频率也可能是不同的. 故B错误.
【正确解答】只有选项D是正确的,符合频率与概率的意义.
【方法规律】审题时一定要分清频率、概率的意义. 概率是等可能条件下事件发生的可能性大小,它是由该随机事件的本质所决定的,与试验条件及次数无关. 而在相同条件下,如果试验次数足够多,那么试验的频率得到相对稳定的值,可利用这个值来估计该事件发生的概率.
二、 对推断、决策的选择有误
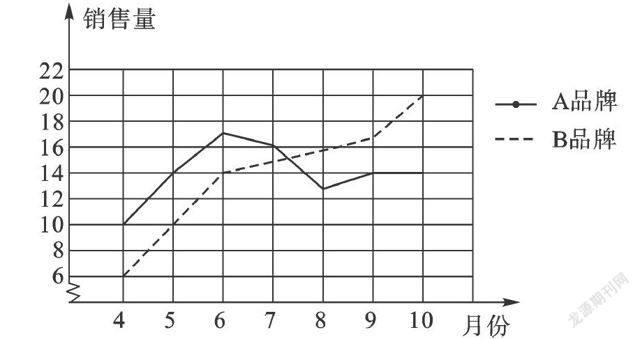
例2 某商场连续7个月统计了A、B两种品牌冰箱的销售情况,并将获得的数据绘制成折线统计图.
(1) 分别求这7个月中,A、B两种品牌冰箱销售量的平均数、中位数和方差;
(2) 对该商场今后的进货情况提出你的建议.
【错误解答】(1) 由计算可知:=14,A种品牌冰箱销售量中位数为14,S2 A=4.3;=14,B种品牌冰箱销售量中位数为15,S2 B=18.6.
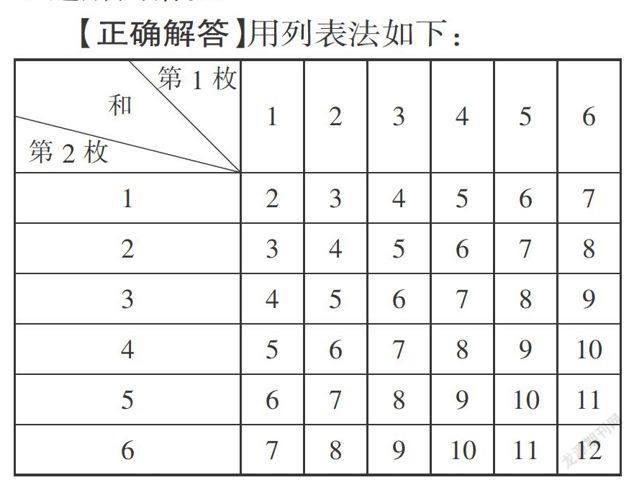
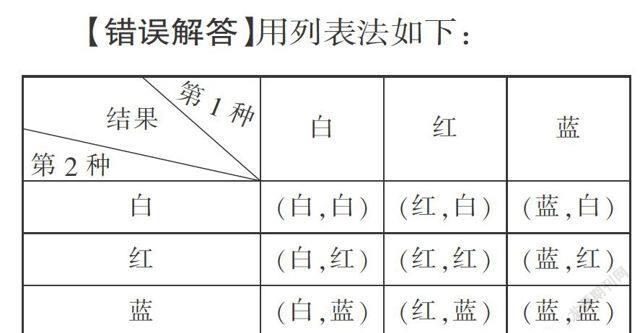
(2) 由于=,S2 A 【错解成因】由于=,无法通过平均数作出推断,接下来最容易想到的就是方差,发现S2 A 【正确解答】建议(2)解答如下:从折线图来看,B型冰箱的月销售量呈上升趋势,若考虑增长势头,进货时可多进B型冰箱. 【方法规律】处理数据时除了要学会分析平均数、中位数、众数外,还要全面观察、分析图形,从而作出正确的推断,特别是折线统计图不但能反映数量的多少,而且能清楚看出数量增减的变化情况. 三、 对等可能性的理解有误 例3 将一枚骰子先后掷两次,求所得的点数之和为6的概率. 【错误解答】抛掷两枚骰子,所能得到的基本事件(即所得的点数之和)有:2、3、4、5、6、7、8、9、10、11、12,共11种情形,而点数之和为6的情况只有1个,所以P(点数之和为6)= . 【错解成因】虽然出现的点数之和确实是只有11种情形,但这些情况不是等可能的,且有些点数之和的情况也不是1个,故上述解法错误. 【正确解答】用列表法如下: ∴共有36种等可能的情况,其中所得的点数之和为6的有5种,∴P(点数之和为6)=. 【方法规律】本题考查的是概率的求法. 如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=. 特别注意,只有在所有等可能事件中才能使用概率计算公式P(A)=进行计算. 而借助树状图、列表法可以不重复不遗漏地列举出所有等可能的情况,可避免犯类似的错误. 四、 有无放回问题的理解有误 例4 已知红色和蓝色在一起可配成紫色,现有三种颜色红、白、蓝,从中任意取出两种颜色来配紫色,问: 能配出紫色的概率是多大? 【错误解答】用列表法如下: ∴共有9种等可能的情况,能配出紫色的有2种,∴P(配出紫色)=. 【错解成因】没有考虑到:在红、白、蓝三种颜色中,任意取出两种颜色时,不能取出两个相同的颜色,这等同于“无放回问题”,这样导致列举出的等可能事件总数产生错误. 【正确解答】用列表法如下: ∴共有6种等可能的情况,能配出紫色的有2种,∴P(配出紫色)= . 【方法规律】本题需要注意在阅读题目时,要正确获取题中的信息. 在以后解决类似的问题时,需要分清题型是属于“有放回”还是“无放回”问题,在这两种不同的情况下,得到的所有等可能情况是完全不同的. 五、 有序与无序的理解有误 例5 袋中装有大小相同的2个红球和2个绿球. 先从袋中摸出1个球后放回,混合均匀后再摸出1个球. 求第一次摸到绿球、第二次摸到红球的概率. 【错误解答1】画树状图得: ∵共有4种等可能的结果,第一次摸到绿球有2种情况,由于放回,第二次摸到红球也有2种情况, ∴P(第一次摸到绿球)==,P(第二次摸到红球)==. 【错解成因】审题不清,题目中的“第一次摸到绿球、第二次摸到红球”是指一个事件,不能把它当成两个事件来求. 【错误解答2】画树状图得: ∵共有16种等可能的结果,摸到一绿球一红球的有8种情况, ∴P(第一次摸到绿球、第二次摸到红球)==. 【错解成因】摸球模型中分有序与无序,不可混淆. 由题目的摸球过程知:摸球的过程是有序的,故第一次摸到绿球、第二次摸到红球与第一次摸到红球、第二次摸到绿球是两种不同的情形,上述解答忽视了摸球的有序性. 【正确解答】画树状图得: ∵共有16种等可能的结果,第一次摸到绿球、第二次摸到红球的情况有4种, ∴P(第一次摸到绿球、第二次摸到红球)==. 【方法规律】分析题目时要仔细观察,有序关心的是摸的过程,先A后B和先B后A 是两个不一样的过程;而无序只关心摸的结果,不必关注先A后B还是先B后A,最终得到的结果都是A和B,不分先后. 小试身手 1. 抛掷一枚质地均匀的硬币,如果连续抛掷1 000次,那么第999次出现正面朝上的概率是( ). A. B. C. D. 无法确定 2. 掷一枚均匀的硬币,出现正面朝上的概率为0.5. 小刚将一枚均匀的硬币掷了100次,可是出现正面朝上的次数却不是50次,他很纳闷,请你帮他解释一下为什么. 3. 一个家庭有3个孩子,求这个家庭中有2个女孩和1个男孩的概率. 4. 为了从甲、乙两名学生中选拔一人参加今年六月份的全县中学生数学竞赛,每个月对他们的学习水平进行一次测验,如图是两人赛前5次测验成绩的折线统计图. (1) 分别求出甲、乙两名学生5次测验成绩的平均数及方差; (2) 如果你是他们的辅导教师,应选派哪一名学生参加这次数学竞赛. 请结合所学统计知识说明理由. 5. 王强与李刚两位同学在学习“概率”时,做抛骰子(均匀正方体形状)实验,他们共抛了54次,出现向上点数的次数如下表: 王强说:“根据实验,一次试验中出现向上点数为5的概率最大. ” 李刚说:“如果抛540次,那么出现向上点数为6的次数正好是100次. ” 请判断王强和李刚说法的对错.
